Similar presentations:
Регрессионный анализ. y = ax+b
1. ЛЕКЦИЯ 10
y = ax+bРЕГРЕССИОННЫЙ
АНАЛИЗ
2. 10.1. Общее представление о регрессии
3.
Зная коэффициенткорреляции, исследователь
не может предсказать, чему в
среднем будет равен признак
y при заданном значении
признака x
4. Для предсказания средних значений признака y необходимо знать вид его функциональной зависимости от x:
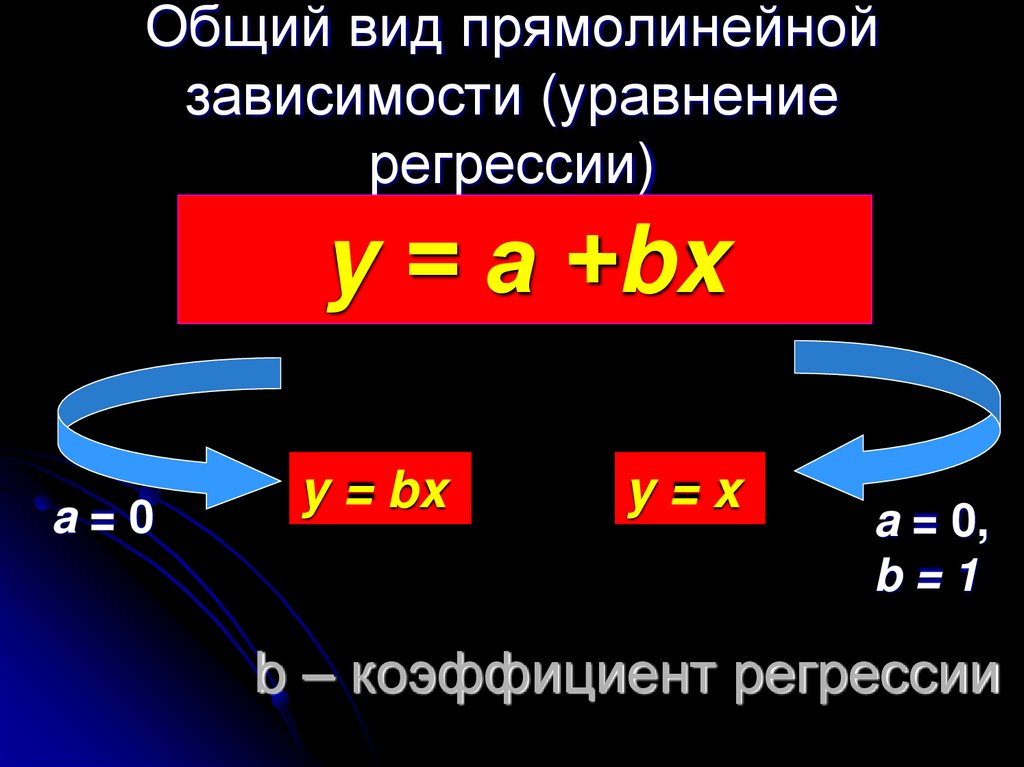
y f (x)5. Общий вид прямолинейной зависимости (уравнение регрессии)
y = а +bxa=0
y = bx
y=x
a = 0,
b=1
b – коэффициент регрессии
6. Обозначения:
х – независимая переменная(independent variable);
y – зависимая переменная
(dependent variable)
у|х - набор значений у,
соответствующих определенному
значению x
7. Задачи регрессионного анализа:
Выразить любую формукорреляционной связи
функционально;
Рассчитать коэффициенты
регрессионного уравнения и
оценить их статистическую
значимость.
8. 10.2. Оценка параметров регрессионного уравнения по выборке
9. Рассматриваемая регрессионная модель требует выполнения следующих условий:
среднее значение μy|x линейнозависит от х
для любого х значения у|х
распределены нормально
стандартное отклонение σy|x
одинаково при всех значениях х.
10. Обозначения выборочных оценок коэффициентов уравнения:
a→αb→β
уравнение регрессии:
у = а + bх
11.
Метод наименьших квадратов(МНК):
позволяет найти регрессионную
прямую, сумма квадратов
расстояний от которой до всех
точек выборки минимальна.
12. Расчет коэффициента регрессии по МНК:
(y
y
)(
x
x
)
i
i
by| x
2
(
x
x
)
i
13. Свободный член уравнения можно рассчитать проще:
a y | x y by | x xПоскольку регрессионная прямая всегда
проходит через точку с координатами
( x; y )
14. 10.3. Разброс значений вокруг регрессионной прямой
15. Выборочная оценка разброса точек – остаточное стандартное отклонение:
s y| x[
y
(
a
bx
)]
i
i
n 2
2
16. 10.4. Стандартные ошибки коэффициентов регрессионного уравнения
17. Стандартная ошибка коэффициента регрессии y|x:
[ ( yi y )( xi x )]( yi y )
2
( xi x )
sby|x
2
(n 2) ( xi x )
2
!!!!
2
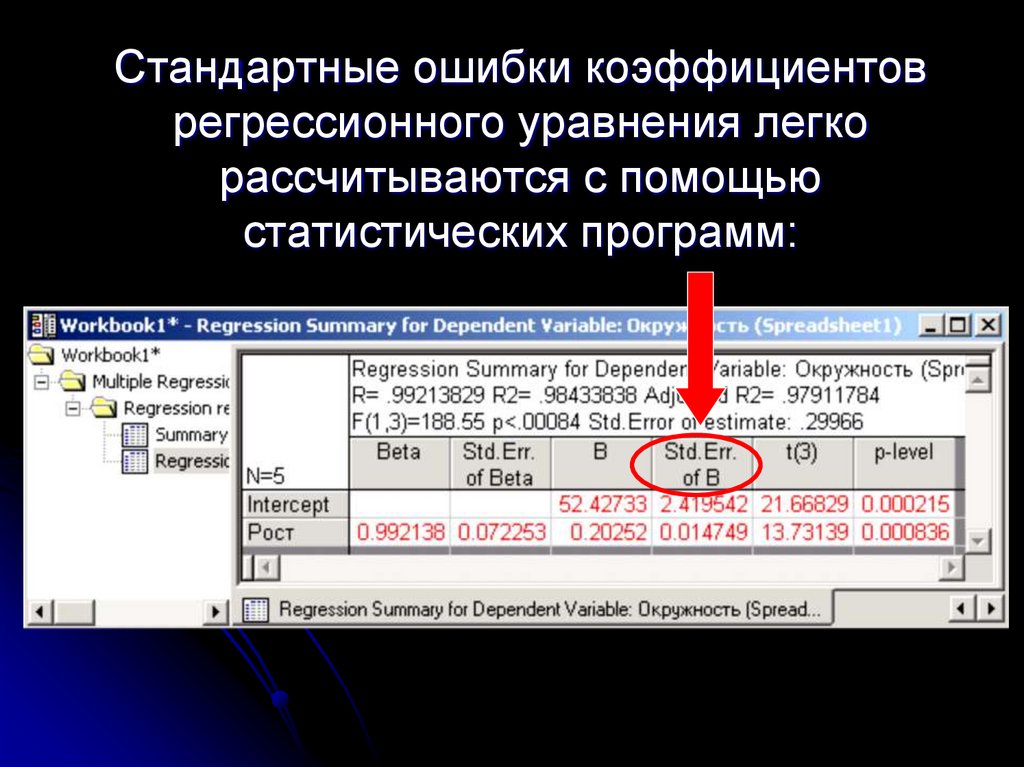
18. Стандартные ошибки коэффициентов регрессионного уравнения легко рассчитываются с помощью статистических программ:
19. 10.5. Оценка статистической значимости регрессии
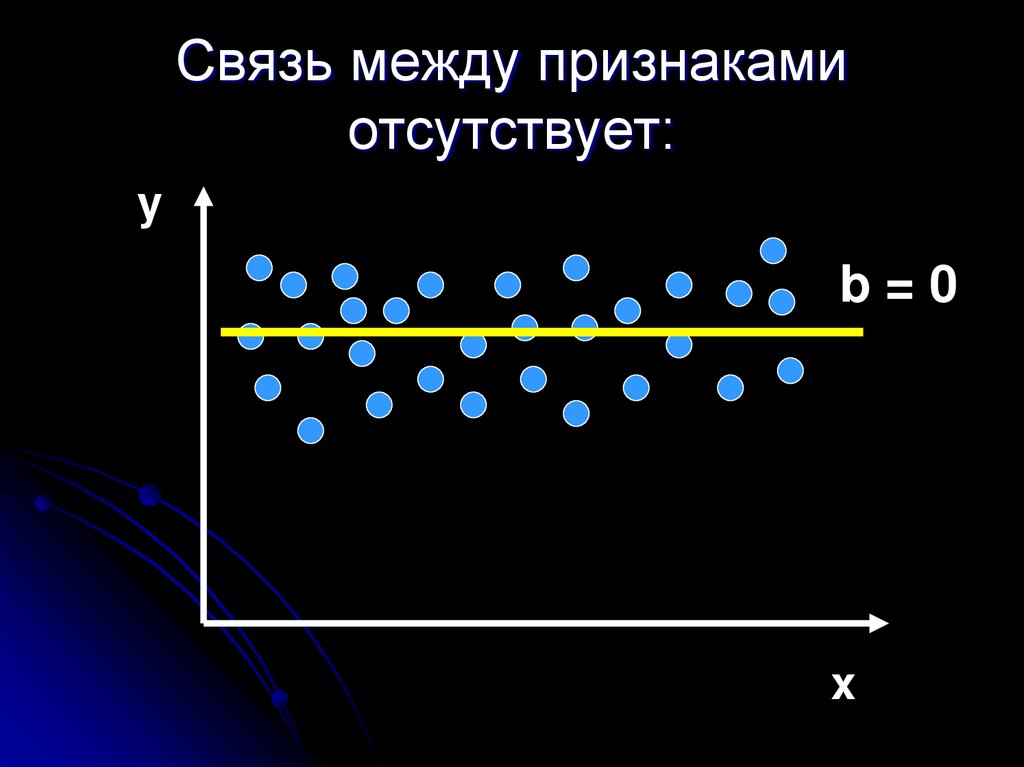
20. Связь между признаками отсутствует:
yb=0
x
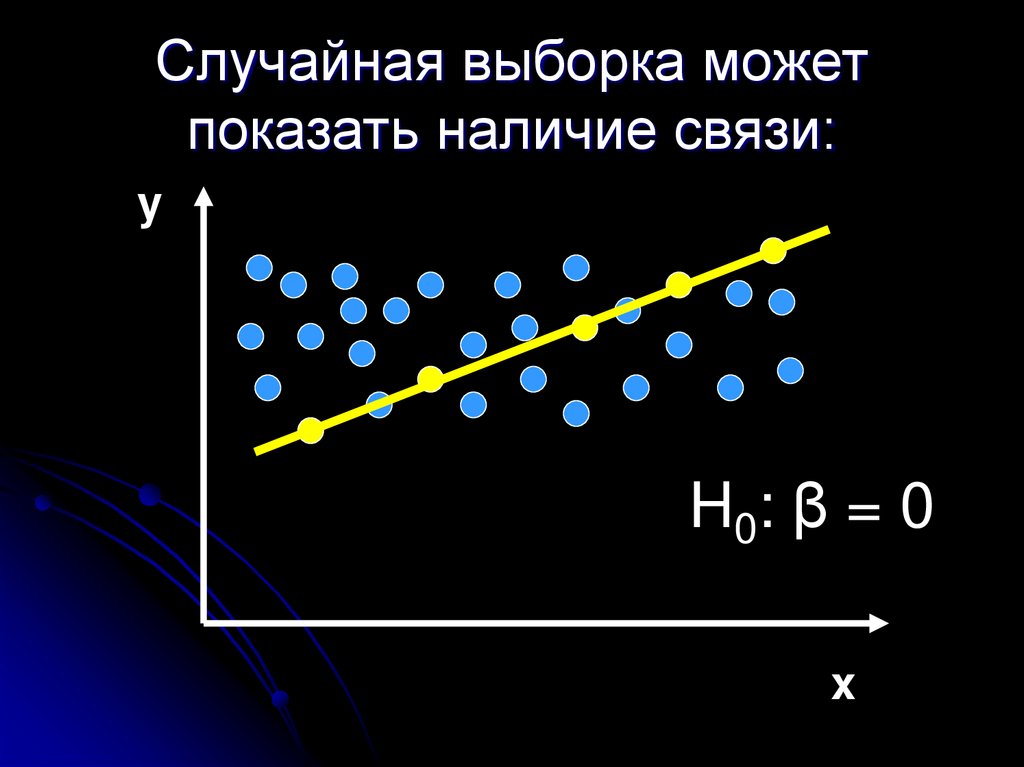
21. Случайная выборка может показать наличие связи:
yH0 : β = 0
x
22. Проверка гипотезы H0: β = 0
bt
sb
b
t
sb


















 mathematics
mathematics








