Similar presentations:
Корреляционный и регрессионный анализы. (Лекция 8)
1. Корреляционный и регрессионный анализы
1.2.
3.
Основные задачи теории
корреляции.
Корреляционный анализ.
Регрессионный анализ.
2. Функциональная зависимость:
каждому возможному значениюпеременной х ставится в
соответствие единственное значение
переменной y.
3.
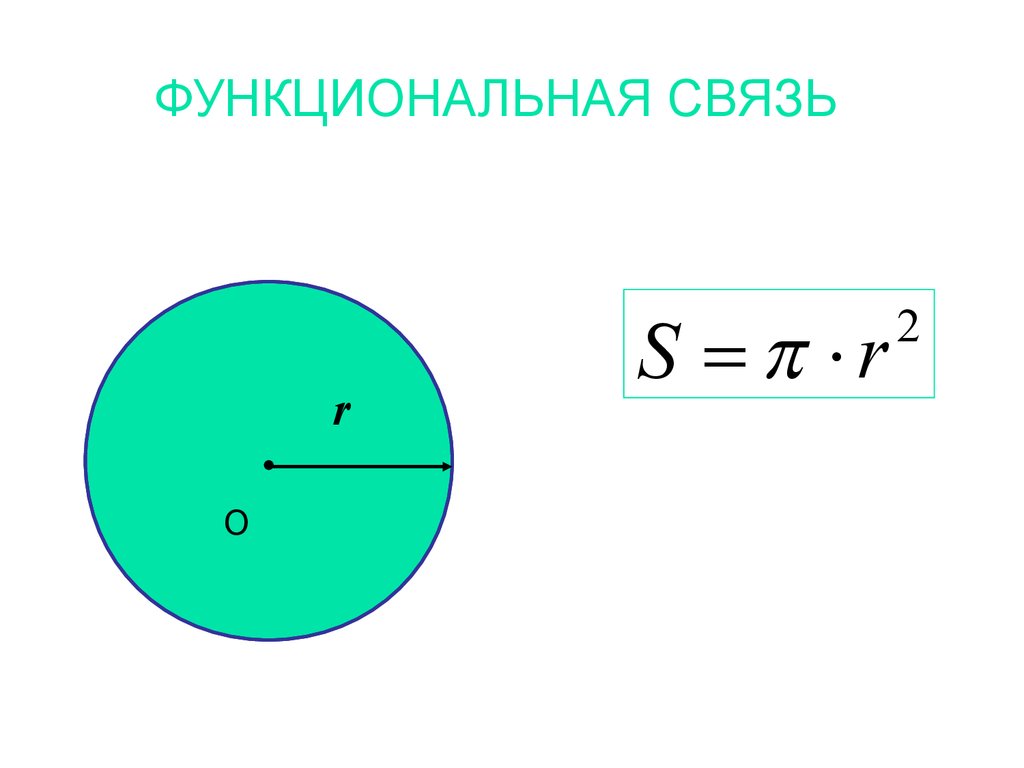
ФУНКЦИОНАЛЬНАЯ СВЯЗЬr
O
S r
2
4.
ФУНКЦИОНАЛЬНАЯ СВЯЗЬS
S v t
5.
ФУНКЦИОНАЛЬНАЯ СВЯЗЬ6. Стохастической зависимостью
называют зависимость, при которойизменение одной из величин влечет
изменение распределения другой.
7. Корреляционной зависимостью
называют зависимость, при которойизменение одной из величин влечет
изменение среднего значения другой.
8.
Годы1-й
Темп
прироста
0
населения
Число
зарегист671
рированных
преступлений
2-й
3-й
4-й
5-й
6-й
7-й
8-й
9-й
10-й
0,9
2
3,4
4,7
6,1
7,4
8,8
9,7
10,7
552
558
553
679
614
647
706
732
699
3
4
5
6
7
8
9
800
700
600
500
0
1
2
10
11
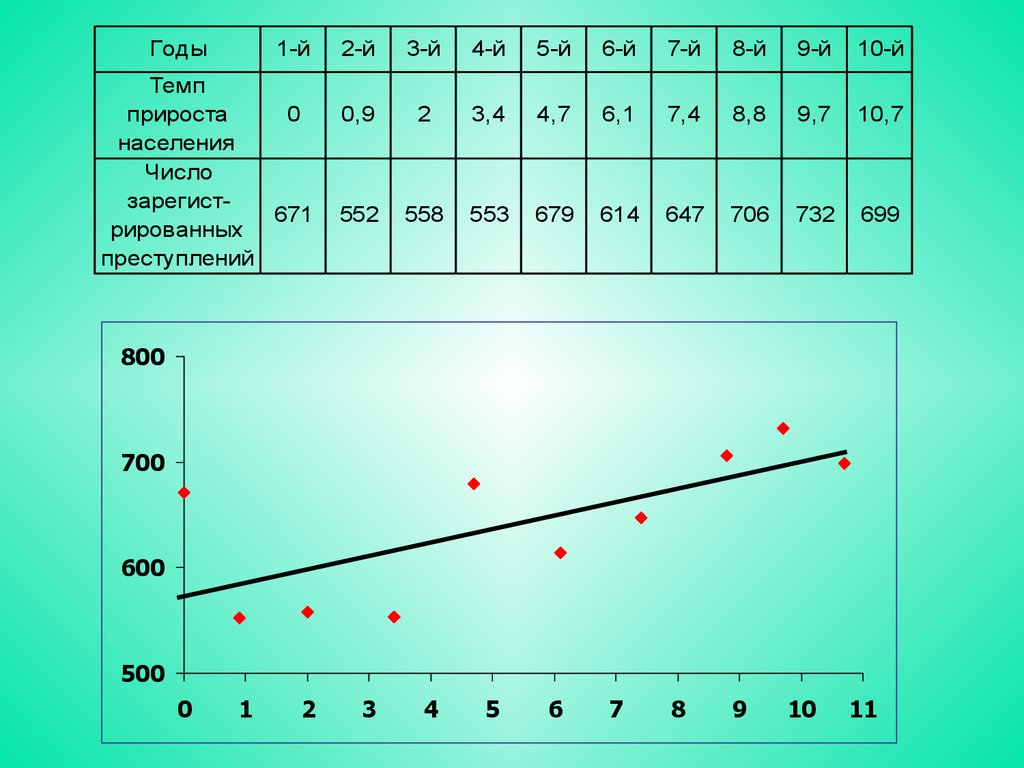
9. Линия регрессии – это графическое представление ведущей тенденции связи между количественными признаками.
800700
600
500
0
1
2
3
4
5
6
7
8
9
10
11
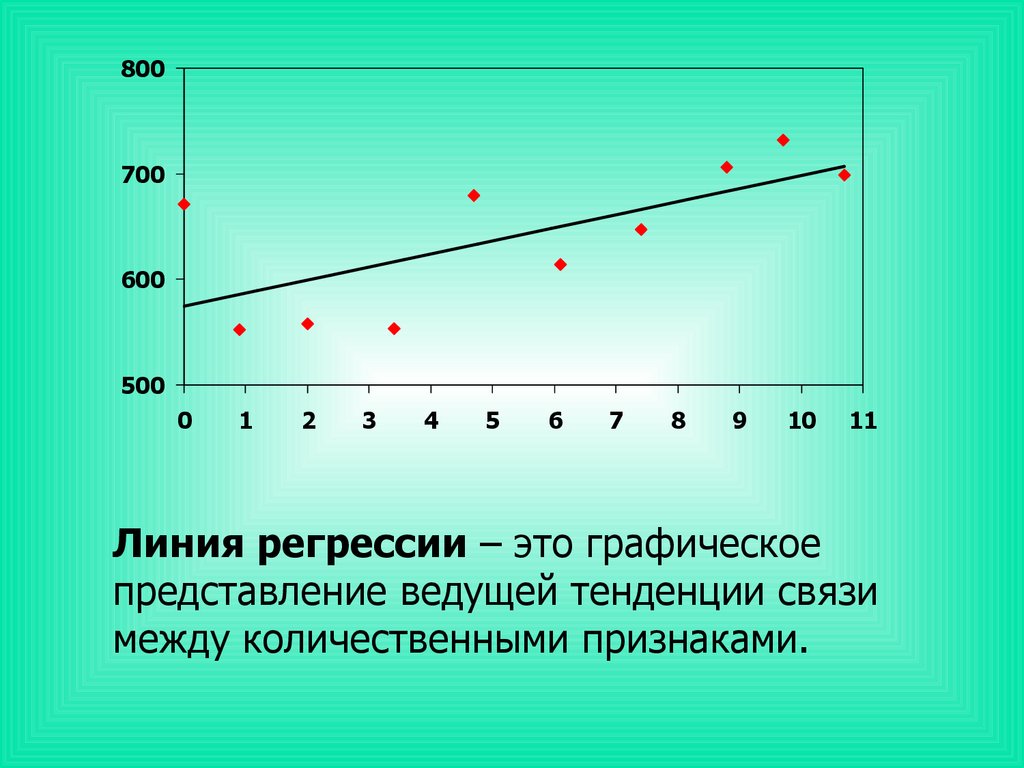
Линия регрессии – это графическое
представление ведущей тенденции связи
между количественными признаками.
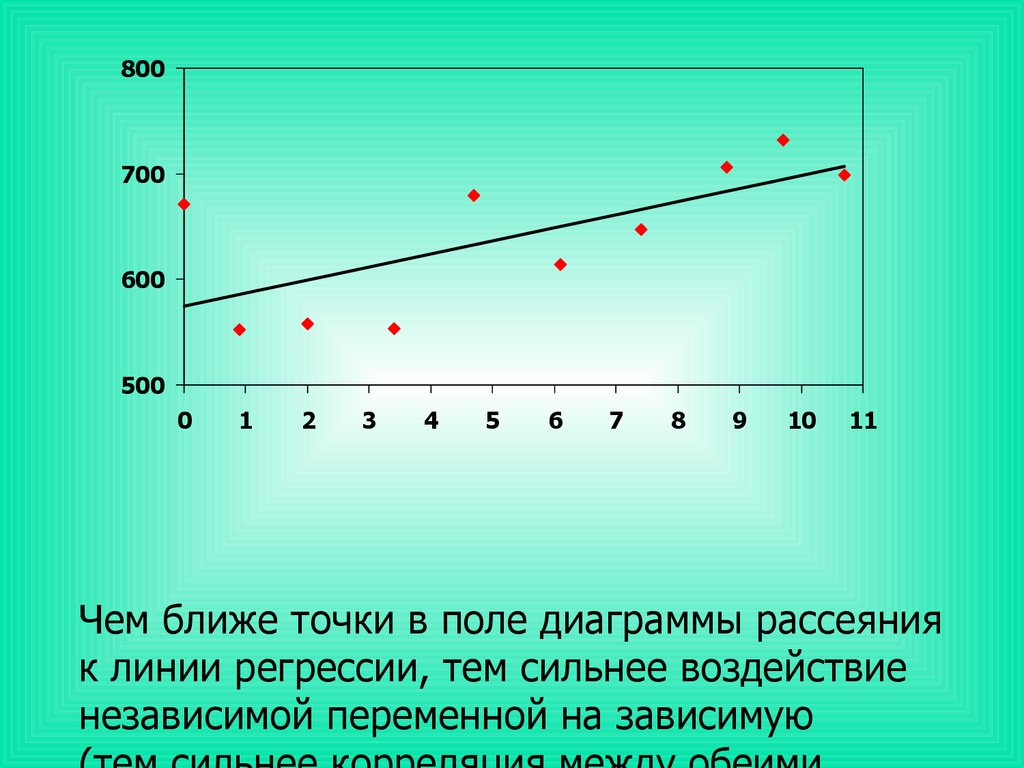
10. Чем ближе точки в поле диаграммы рассеяния к линии регрессии, тем сильнее воздействие независимой переменной на зависимую (тем сильнее кор
800700
600
500
0
1
2
3
4
5
6
7
8
9
10
11
Чем ближе точки в поле диаграммы рассеяния
к линии регрессии, тем сильнее воздействие
независимой переменной на зависимую
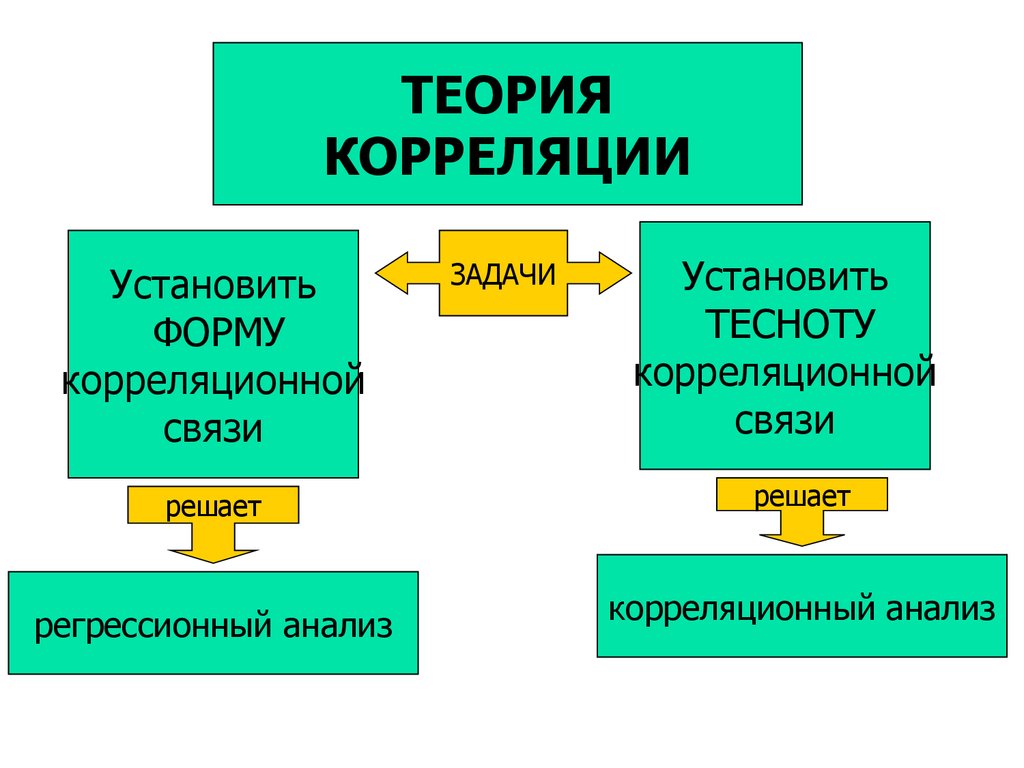
11.
ТЕОРИЯКОРРЕЛЯЦИИ
Установить
ФОРМУ
корреляционной
связи
решает
регрессионный анализ
ЗАДАЧИ
Установить
ТЕСНОТУ
корреляционной
связи
решает
корреляционный анализ
12. Корреляционный анализ
1.2.
3.
Коэффициент линейной корреляции
Пирсона.
Свойства коэффициента корреляции.
Оценка значения коэффициента
корреляции.
13. Простой (выборочный) коэффициент корреляции Пирсона
Номер наблюденияX
Y
1
x1
x2
y1
y2
…
…
xn
yn
2
…
n
rX ,Y
n
n
n
i 1
i 1
i 1
n xi yi xi yi
n
n
n
n
i 1
i 1
i 1
i 1
(n ( xi ) 2 ( xi ) 2 ) (n ( yi ) 2 ( yi ) 2 )
;
14. Свойства коэффициента корреляции
1Свойства коэффициента корреляции
1. Величина коэффициента корреляции
заключена в пределах
-1 r 1,
15. Свойства коэффициента корреляции
Y-1 < r a< 0
Y
0 < r б< 1
б
а
X
Y
X
Y
|r в|> | r a|
| r г| > | r б |
в
г
X
X
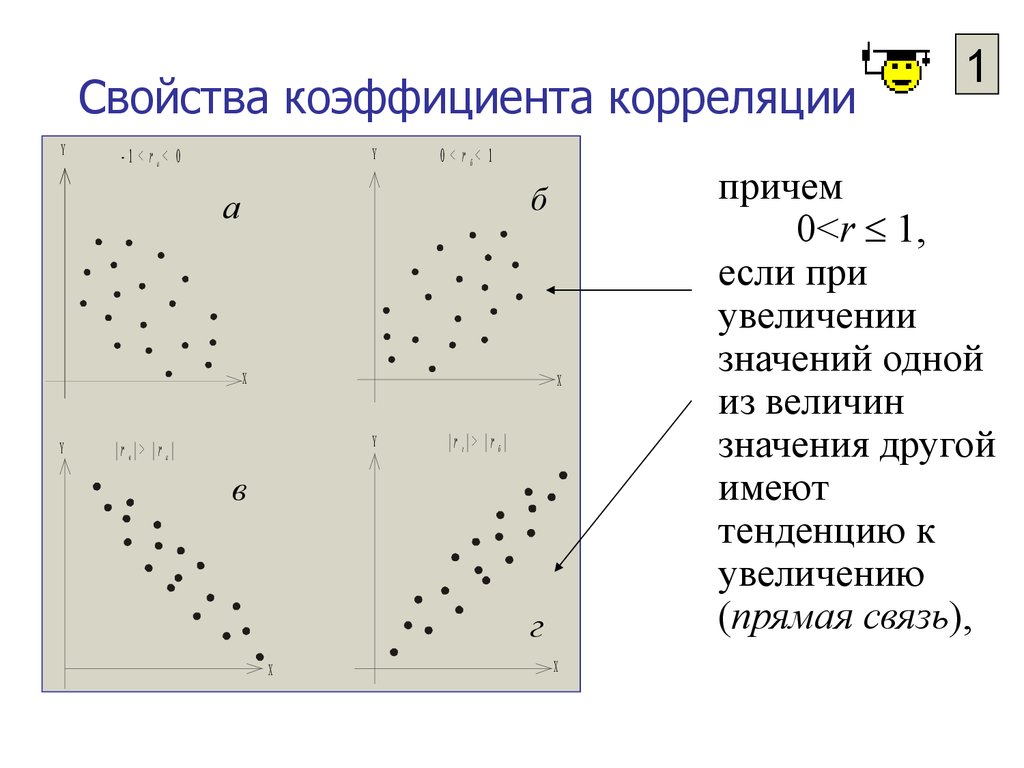
1
причем
0<r 1,
если при
увеличении
значений одной
из величин
значения другой
имеют
тенденцию к
увеличению
(прямая связь),
16. Свойства коэффициента корреляции
Y-1 < r a< 0
Y
0 < r б< 1
X
Y
и
б
а
X
Y
|r в|> | r a|
| r г| > | r б |
в
г
X
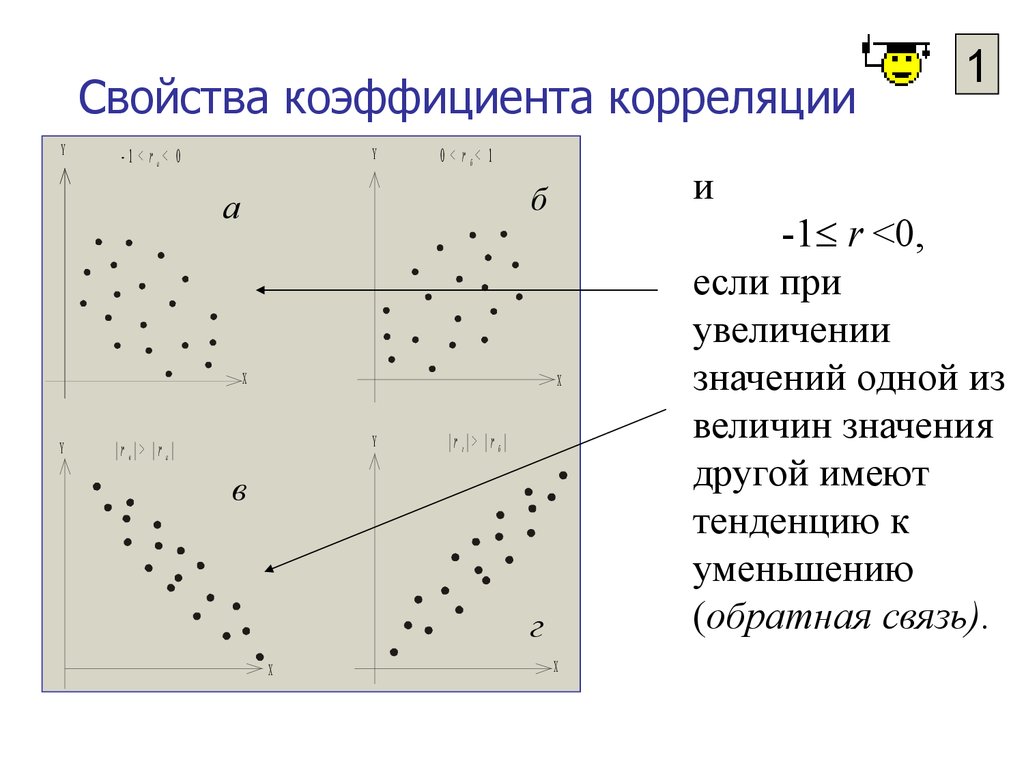
1
X
-1 r <0,
если при
увеличении
значений одной из
величин значения
другой имеют
тенденцию к
уменьшению
(обратная связь).
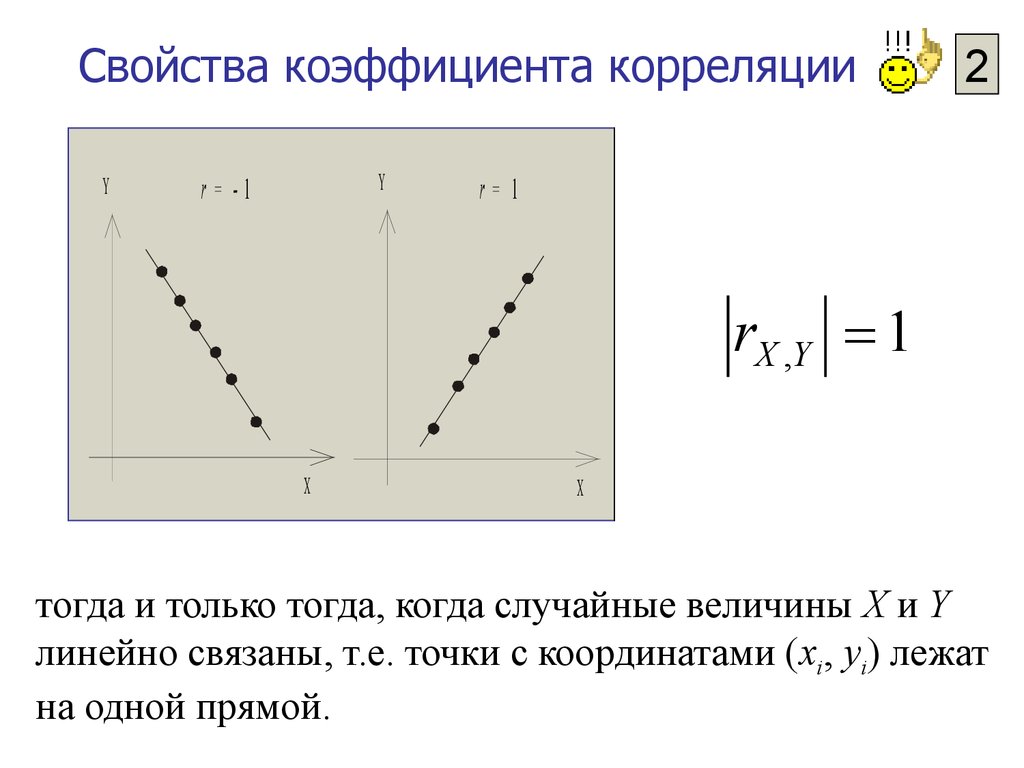
17. Свойства коэффициента корреляции
YY
r= -1
r= 1
Y
2
r= 0
rX ,Y 1
X
X
X
тогда и только тогда, когда случайные величины X и Y
линейно связаны, т.е. точки с координатами (xi, yi) лежат
на одной прямой.
18. Свойства коэффициента корреляции
Y-1 < r a< 0
Y
0 < r б< 1
б
а
X
Y
X
Y
|r в|> | r a|
| r г| > | r б |
в
г
X
3
X
Чем ближе rX ,Y к
единице, тем
сильнее линейная
связь между
случайными
величинами, т.е.
тем меньше точки
с координатами
(xi, yi) рассеяны
около прямой.
19. Свойства коэффициента корреляции
Y-1 < r a< 0
Y
0 < r б< 1
X
Y
X
Y
|r в|> | r a|
X
3
| r г| > | r б |
X
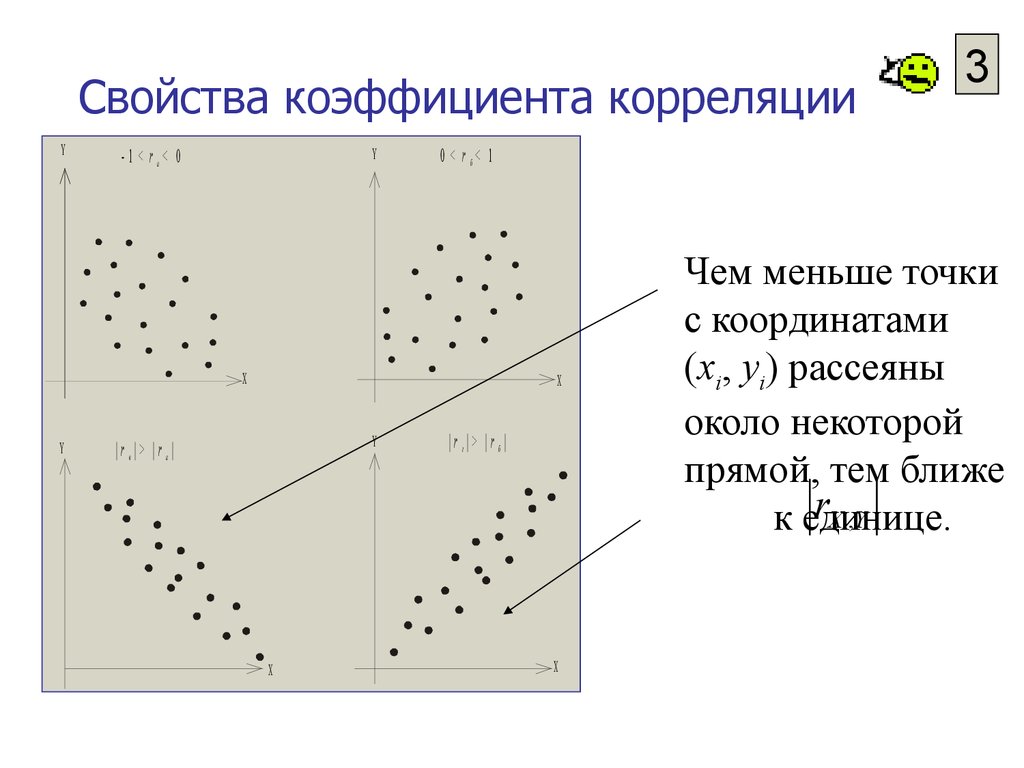
Чем меньше точки
с координатами
(xi, yi) рассеяны
около некоторой
прямой, тем ближе
rX ,Y
к единице.
20. Свойства коэффициента корреляции
Y1
r= 1
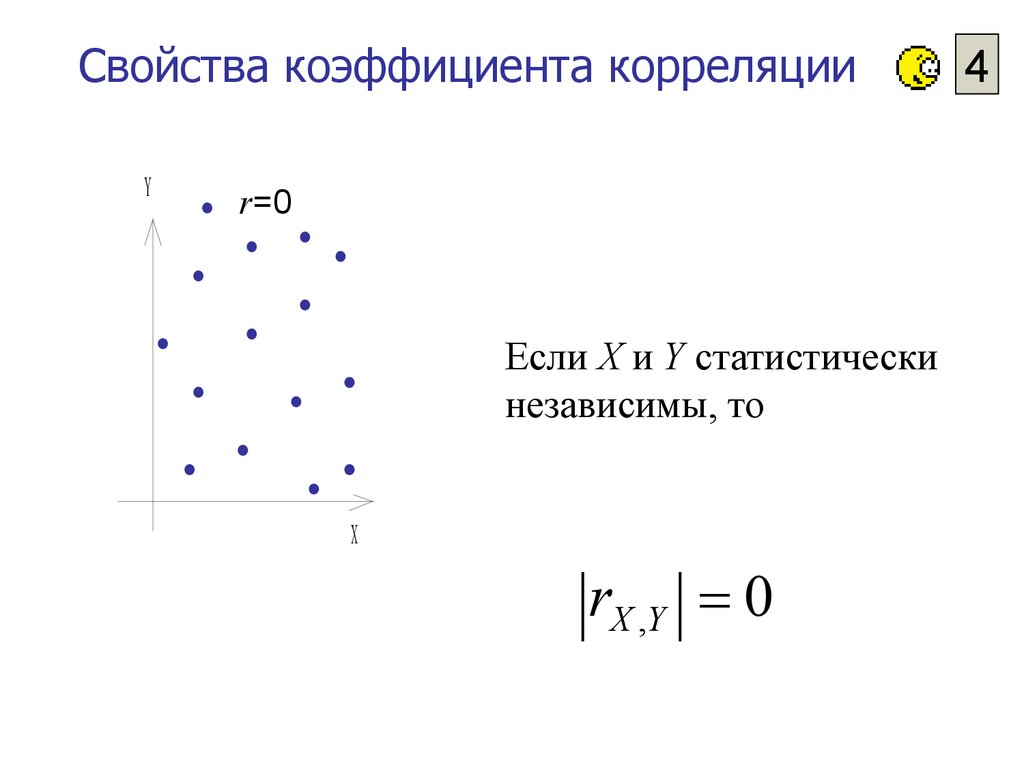
r=0
Y
r= 0
Если X и Y статистически
независимы, то
X
X
X
rX ,Y 0
4
21. Свойства коэффициента корреляции
XСвойства коэффициента корреляции
Y
r= 1
r=0
Y
r= 0
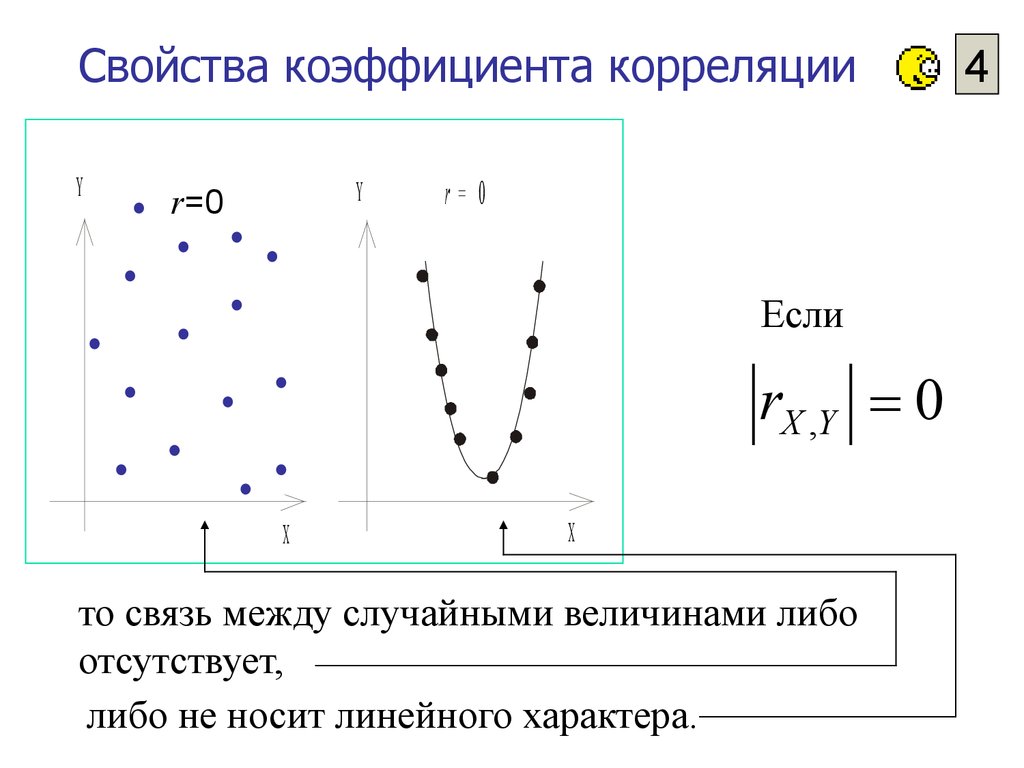
Если
rX ,Y 0
X
X
то связь между случайными величинами либо
отсутствует,
либо не носит линейного характера.
4
22. Свойства коэффициента корреляции
5Для нормально распределенных Х и Y из того, что
rX ,Y 0
f(x)
1
2
1
2 e
следует их независимость.
O
a–
a
a+
x
23. Оценка значения коэффициента корреляции
24.
1) оценка тесноты статистическойлинейной связи по абсолютному значению r:
r 0 – связь отсутствует;
r 0,3 – связь слабая;
0,3 < r 0,5 – связь умеренная;
0,5< r 0,7 – связь значительная;
0,7 < r 0,9 – связь сильная;
0,9 < r – очень сильная;
r = 1– функциональная связь.
25. 2) оценка направления статистической линейной связи по знаку r:
знак «+» – прямая связь,знак «–» – обратная связь.
26.
3) оценка значимости полученногорезультата:
Уровень значимости , говорит о том, с какой
надежностью =(1- ) 100% можно доверять
полученному результату.
Если близок к нулю, можно доверять
вычисленному значению коэффициента
корреляции;
когда >0,2, к значению коэффициента
корреляции следует относиться с большой
осторожностью.
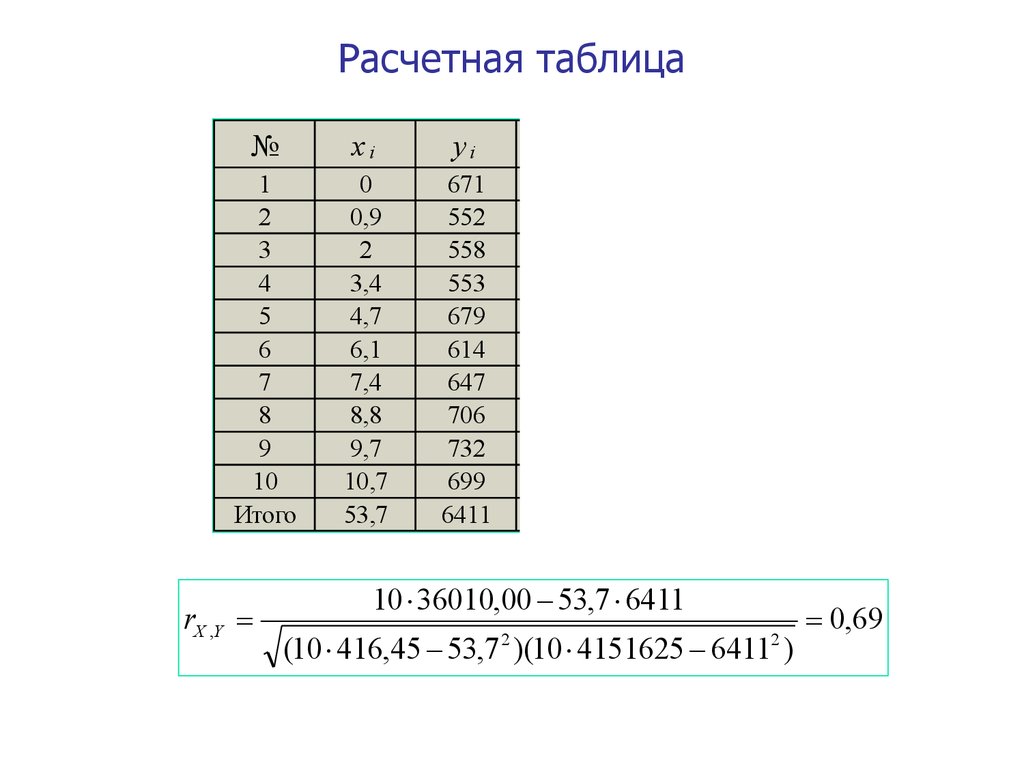
27. Расчетная таблица
№хi
yi
1
2
3
4
5
6
7
8
9
10
Итого
0
0,9
2
3,4
4,7
6,1
7,4
8,8
9,7
10,7
53,7
671
552
558
553
679
614
647
706
732
699
6411
rX ,Y
хi
2
yi
2
0
450241
0,81
304704
4
311364
11,56 305809
22,09 461041
37,21 376996
54,76 418609
77,44 498436
94,09 535824
114,49 488601
416,45 4151625
хiyi
0
496,8
1116
1880,2
3191,3
3745,4
4787,8
6212,8
7100,4
7479,3
36010
10 36010,00 53,7 6411
(10 416,45 53,7 )(10 4151625 6411 )
2
2
0,69
28.
rX ,Y10 36010,00 53,7 6411
(10 416,45 53,7 2 )(10 4151625 64112 )
0,69
связь значительная ( r = 0,69 0,5< r 0,7),
прямая (знак «+»).
29. Регрессионный анализ
1.2.
3.
Классификация.
Основные задачи.
Анализ адекватности модели.
30. I. Классификация
31. 1.В зависимости от числа явлений
– простой (регрессия между двумяпеременными);
– множественной (регрессия между зависимой
переменной Y и несколькими независимыми
переменными (X1, X2, …, Xn)).
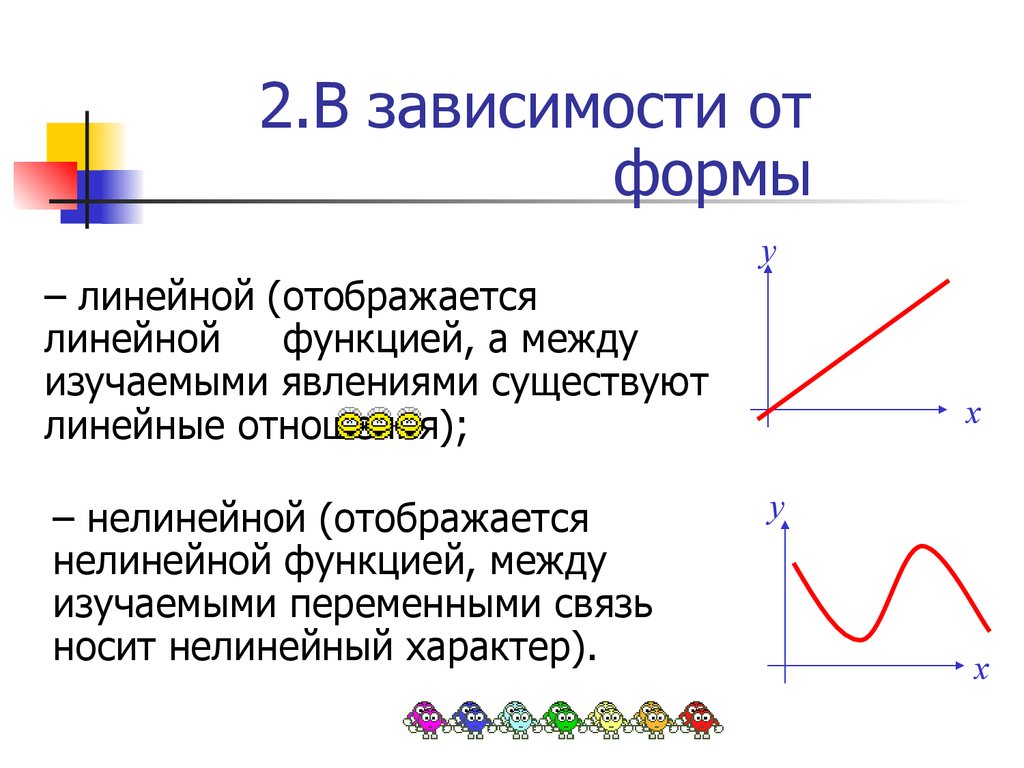
32. 2.В зависимости от формы
у– линейной (отображается
линейной
функцией, а между
изучаемыми явлениями существуют
линейные отношения);
– нелинейной (отображается
нелинейной функцией, между
изучаемыми переменными связь
носит нелинейный характер).
х
у
х
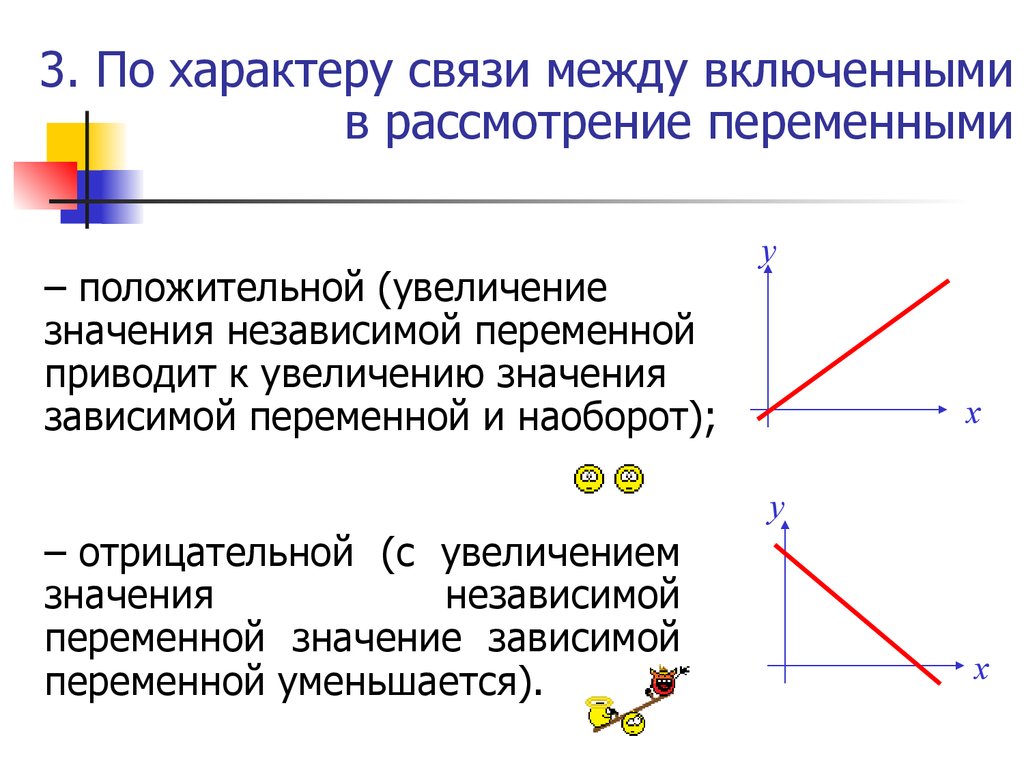
33. 3. По характеру связи между включенными в рассмотрение переменными
– положительной (увеличениезначения независимой переменной
приводит к увеличению значения
зависимой переменной и наоборот);
у
х
у
– отрицательной (с увеличением
значения
независимой
переменной значение зависимой
переменной уменьшается).
х
34. 4. По типу
– непосредственной (в этом случае причинаоказывает прямое воздействие на следствие, т.е.
зависимая и независимая переменные связаны
непосредственно друг с другом);
– косвенной (независимая переменная оказывает
опосредованное действие через третью или ряд
других переменных на зависимую переменную);
– ложной
(нонсенс
регрессия)
–
может
возникнуть при поверхностном и формальном
подходе к исследуемым процессам и явлениям.
35. II. Основные задачи
36. Основные задачи
1. Определение формы зависимости.2. Отыскание подходящих значений
неизвестных параметров.
3. Оценка неизвестных значений зависимой
переменной.
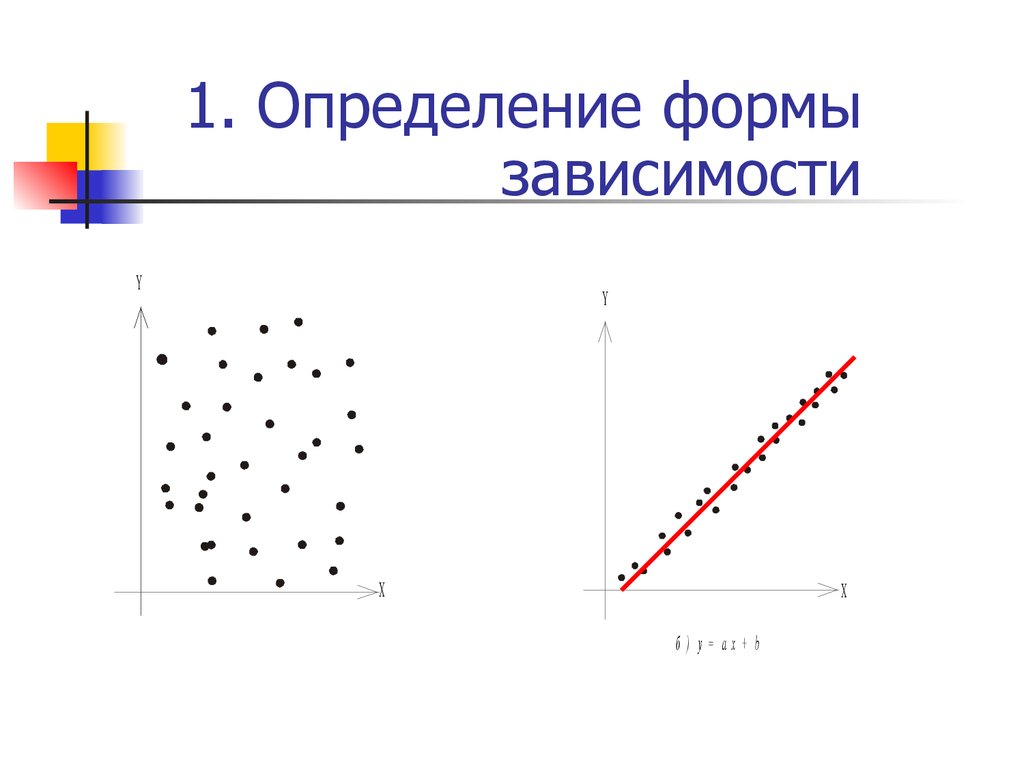
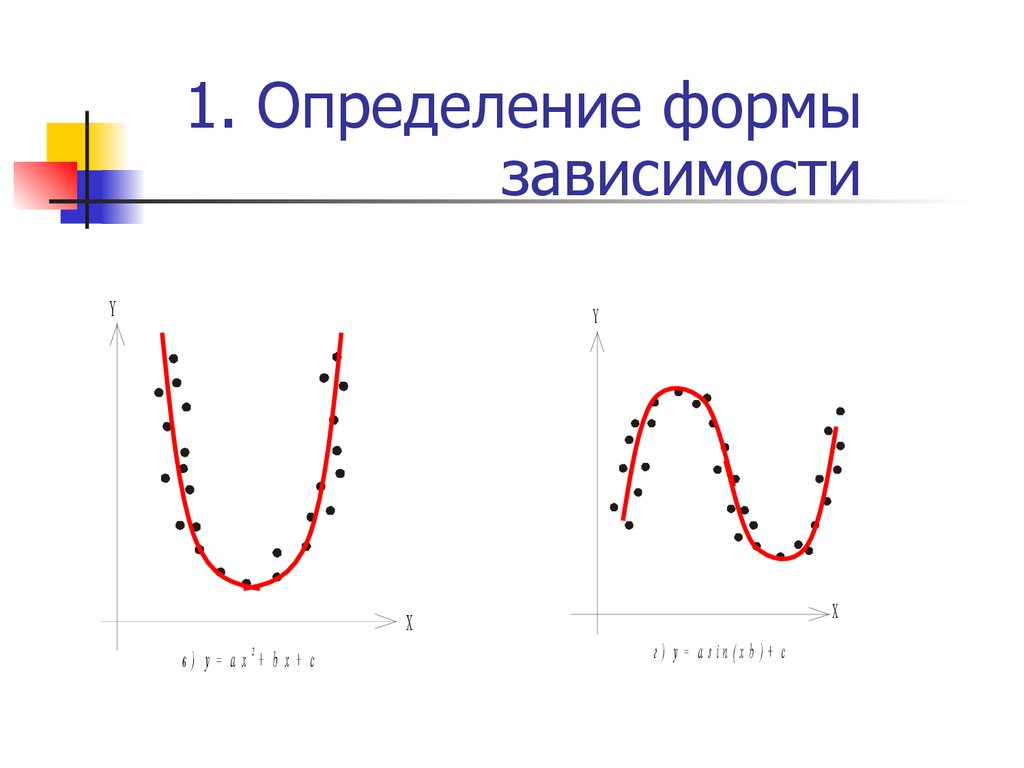
37. 1. Определение формы зависимости
YY
X
а ) свя зь о тсу тствует
X
б) y= ax+ b
38. 1. Определение формы зависимости
YY
X
X
2
в) y= ax + b x+ c
г) y = a sin (x b )+ c
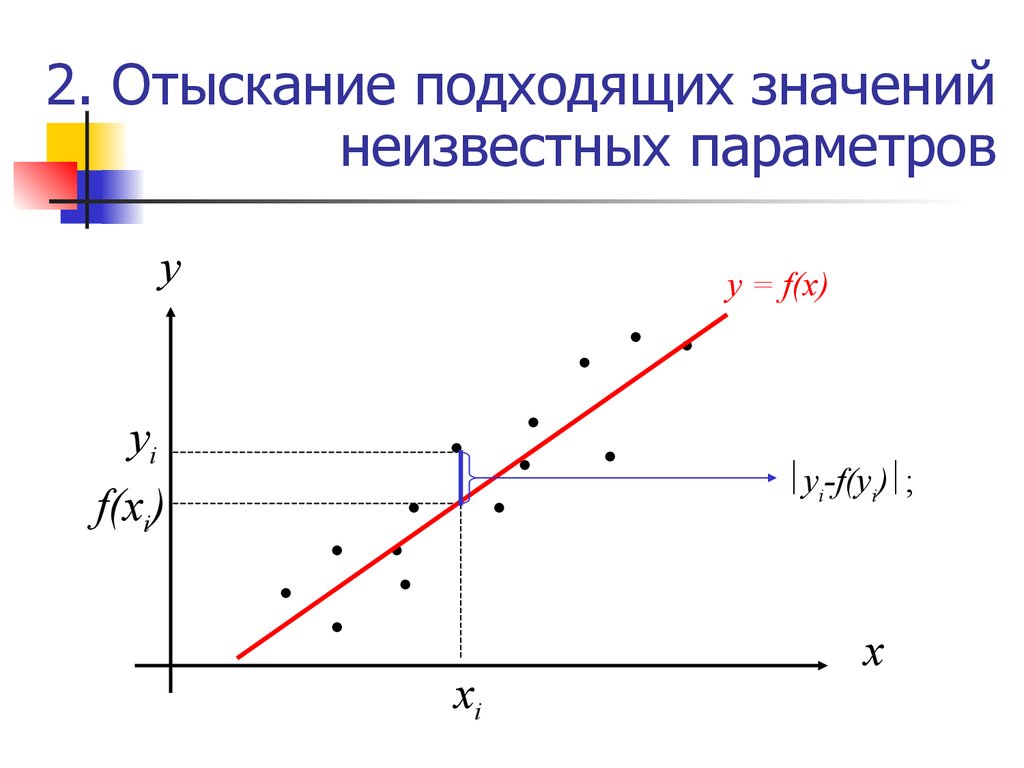
39. 2. Отыскание подходящих значений неизвестных параметров
уy = f(x)
yi
f(xi)
yi-f(yi) ;
хi
х
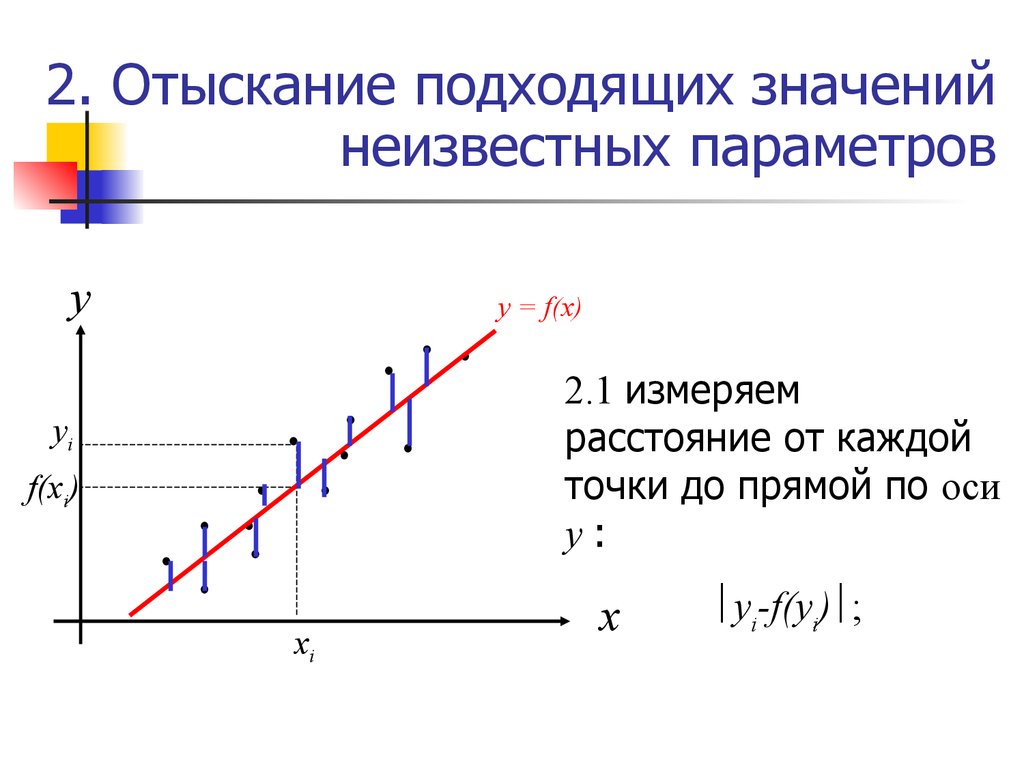
40. 2. Отыскание подходящих значений неизвестных параметров
уy = f(x)
2.1 измеряем
расстояние от каждой
точки до прямой по оси
y:
yi
f(xi)
хi
х
yi-f(yi) ;
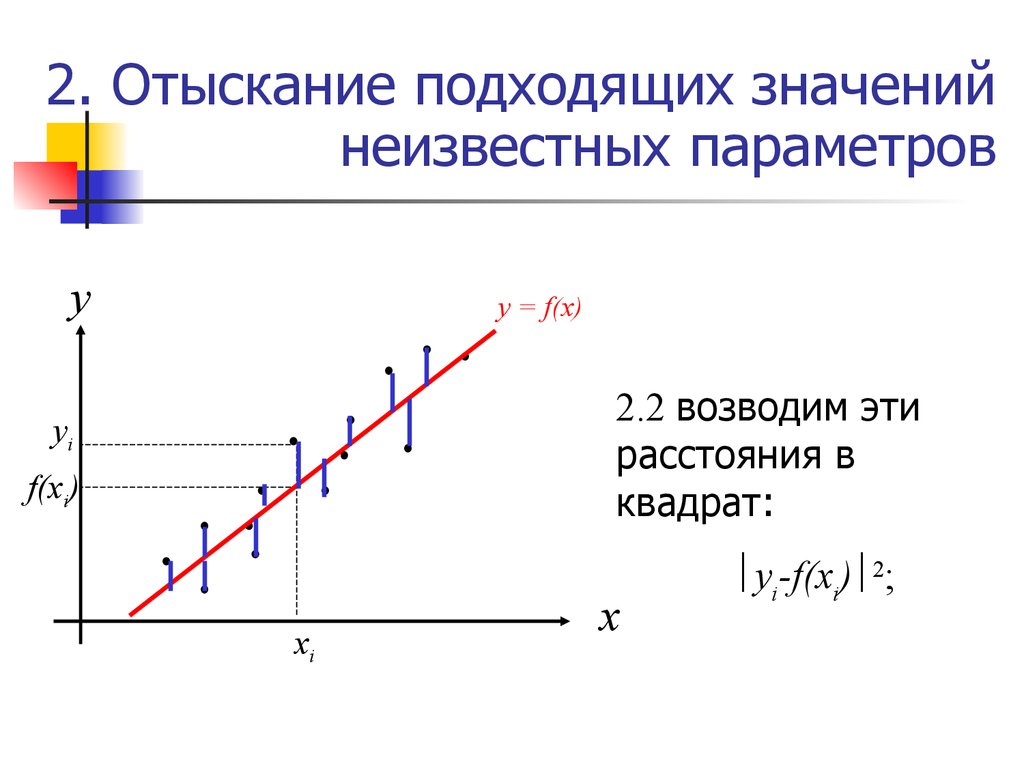
41. 2. Отыскание подходящих значений неизвестных параметров
уy = f(x)
2.2 возводим эти
расстояния в
квадрат:
yi
f(xi)
хi
х
yi-f(xi) 2;
42. 2. Отыскание подходящих значений неизвестных параметров
2.3 суммируем по всем точкам:S= y1-f(x1) 2+ y2-f(x2) 2+...+ yi-f(yi) 2;
2.4 требуем, чтобы полученная сумма
квадратов
расстояний
была
минимальной
S min
43.
В случае линейной регрессии y(x) = ax+ba
n
n
n
i 1
i 1
n
i 1
n xi yi xi yi
n
n xi2 ( xi ) 2
i 1
i 1
b
n
n
n
n
i 1
i 1
n
i 1
n
i 1
2
y
x
i i xi xi yi
n xi2 ( xi ) 2
i 1
i 1
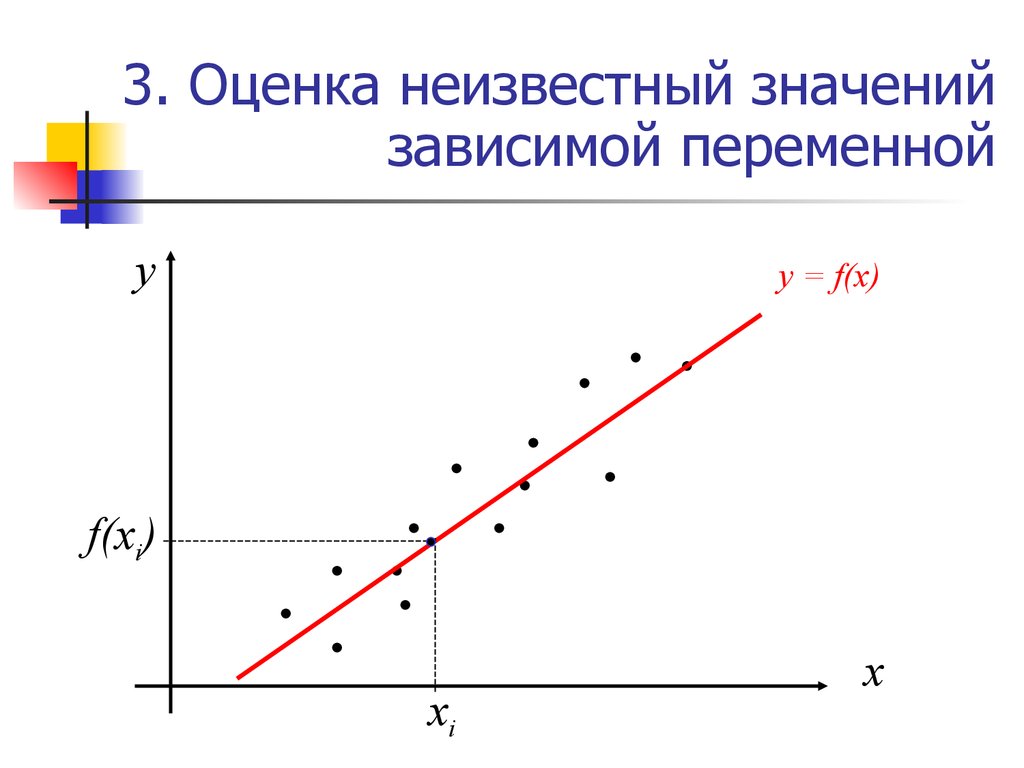
44. 3. Оценка неизвестный значений зависимой переменной
уy = f(x)
f(xi)
хi
х
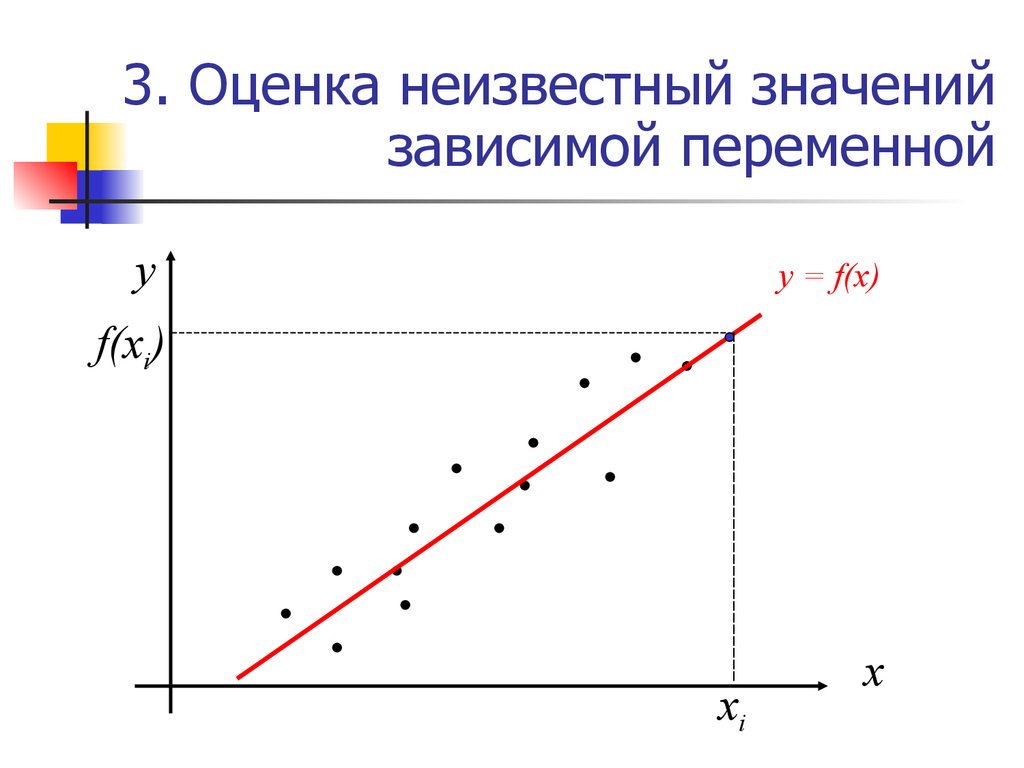
45. 3. Оценка неизвестный значений зависимой переменной
уy = f(x)
f(xi)
хi
х
46. Анализ адекватности модели
47.
Предсказанные значения – значения,соответствующие наблюдаемым независимым
значениям xi, вычисленные согласно уравнению
y=f(x) (будем обозначать yi*).
Остатки – разности между наблюдаемыми
значениями и предсказанными: yi-f(xi)= yi-yi*
48.
y1 y 2 ... y ny
n
SS ( y1 y ) ( y 2 y ) ... ( y n y )
2
2
2
SS Pr ( y1 y ) ( y 2 y ) ... ( y n y )
2
2
2
49. Коэффициент детерминации
SS PrRI
SS
50. Коэффициент детерминации
Свойства:а) 0 RI 1;
б) Чем ближе коэффициент детерминации к
1, тем лучше регрессия «объясняет»
зависимость данных;
в) В случае линейной регрессииRI
r
2
51. Средняя ошибка аппроксимации
yi y1
100%
n i 1
yi
n
*
i
Модель считается адекватной, если
15%
52. Анализ остатков
Если модель подобрана правильно, то- остатки будут вести себя достаточно
хаотично,
- в остатках не будет систематической
составляющей, резких выбросов,
- в чередовании знаков не будет никаких
закономерностей.
53. Порядок действий
при использовании методовкорреляционно-регрессионного анализа
1. Исследование природы
рассматриваемых переменных для
установления типа зависимости между
переменными.
54. Порядок действий
2. Сбор экспериментальных данных,обсуждение вопроса об
ограничениях:
2.1. Случайность выборки: несвязанность i-го
наблюдения с предыдущими и отсутствие
влияния на последующие.
2.2. Однородность дисперсий: рассеяния должны
быть
одинаковыми
для
всех
значений
независимого переменного.
2.3. Нормальность распределений.
55. Порядок действий
3. Построение диаграммы разброса.4. Измерение тесноты связи, вычисление
выборочного коэффициента корреляции.
5. Установление общего вида зависимости
(линейная, параболическая и т.д.)
56. Порядок действий
6. Построение эмпирической линиирегрессии методом наименьших
квадратов.
7. Исследование статистических свойств
регрессионной зависимости, оценка
адекватности модели.



































 mathematics
mathematics








