Similar presentations:
Значения синуса, косинуса и тангенса некоторых углов
1.
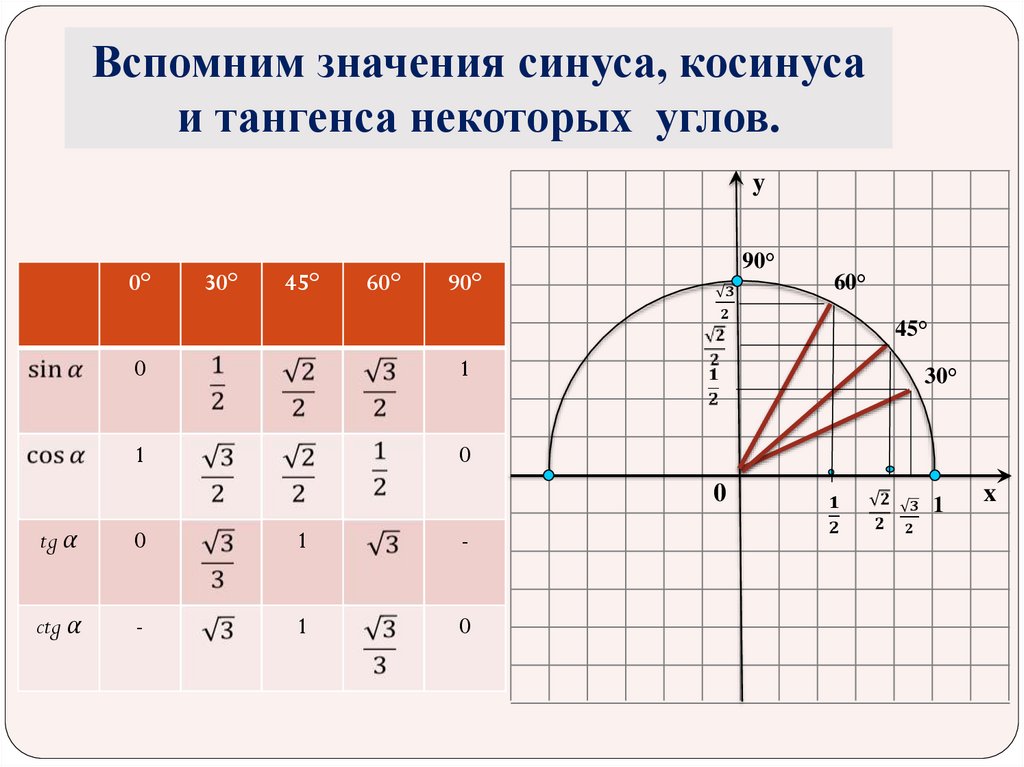
Вспомним значения синуса, косинусаи тангенса некоторых углов.
y
0°
30°
45°
60°
90°
90°
60°
45°
0
1
1
0
30°
0
tg α
0
1
-
ctg α
-
1
0
1
x
2. Задача 1.
Решение:sin (180 - )= sin
cos (180 - ) = - cos
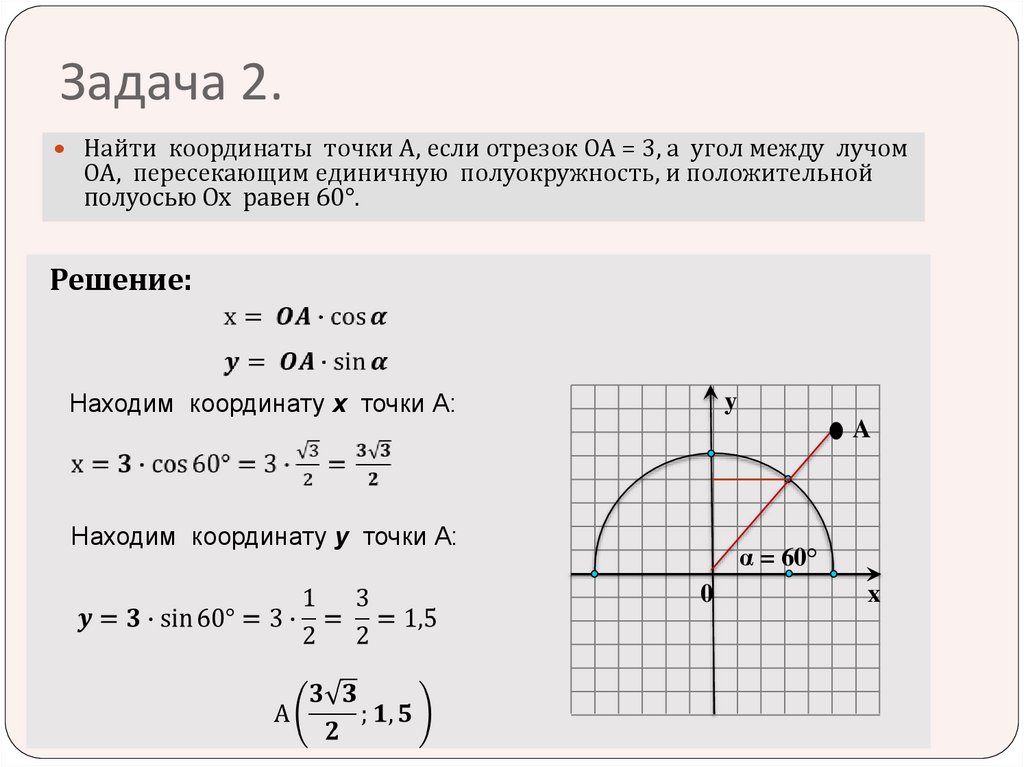
3. Задача 2.
Найти координаты точки А, если отрезок ОА = 3, а угол между лучомОА, пересекающим единичную полуокружность, и положительной
полуосью Ох равен 60°.
Решение:
Находим координату х точки А:
y
A
Находим координату у точки А:
α = 60°
0
x
4. Закончите предложения:
a. « Синусом острого угла прямоугольноготреугольника называется отношение…»
b. « Косинусом острого угла прямоугольного
треугольника называется отношение…»
c. « Тангенсом острого угла прямоугольного
треугольника называется отношение…»
d. « Котангенсом острого угла прямоугольного
треугольника называется отношение…»
5. Определите верны или нет следующие утверждения:
1. Существует прямоугольный треугольник сгипотенузой 8 и катетами 6 и 10
2. В треугольнике любая сторона меньше суммы
двух других сторон.
3. Сумма углов треугольника равна 360
4. В прямоугольном треугольнике синус одного из
углов равен 0.
5. Площадь треугольника равна произведению
основания на высоту.
6. Треугольник со сторонами 2,6, 9 существует.
7. Длина гипотенузы прямоугольного треугольника
больше суммы длин его катетов.
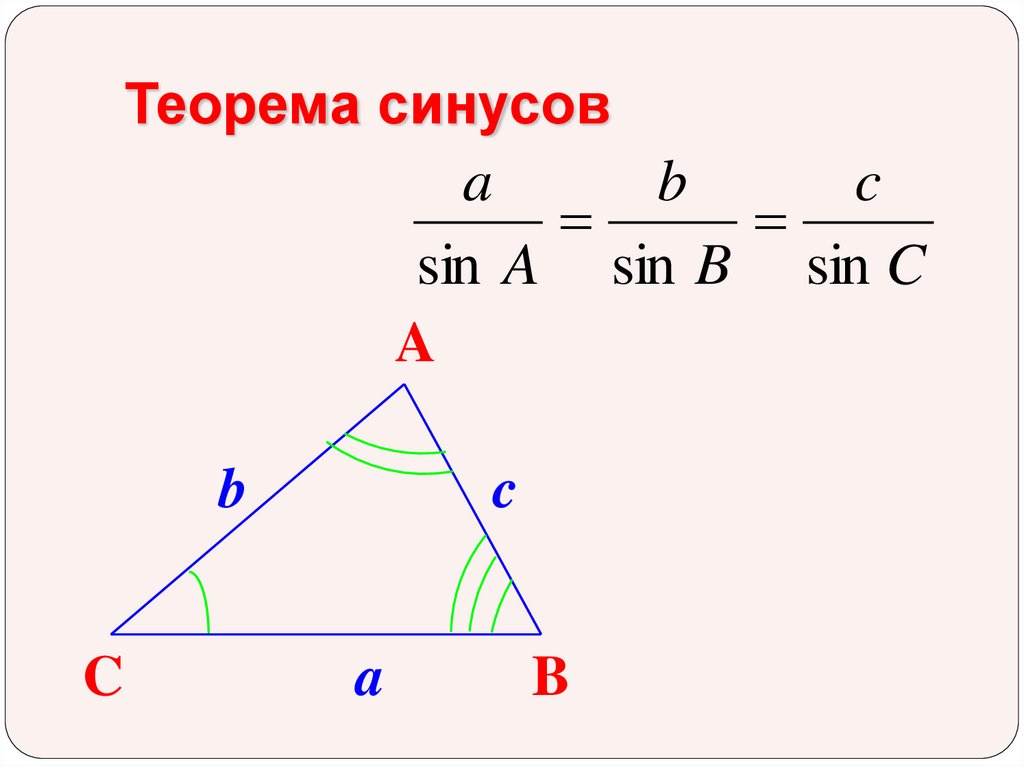
6.
Теорема синусовa
b
c
sin A sin B sin C
A
b
C
c
a
B
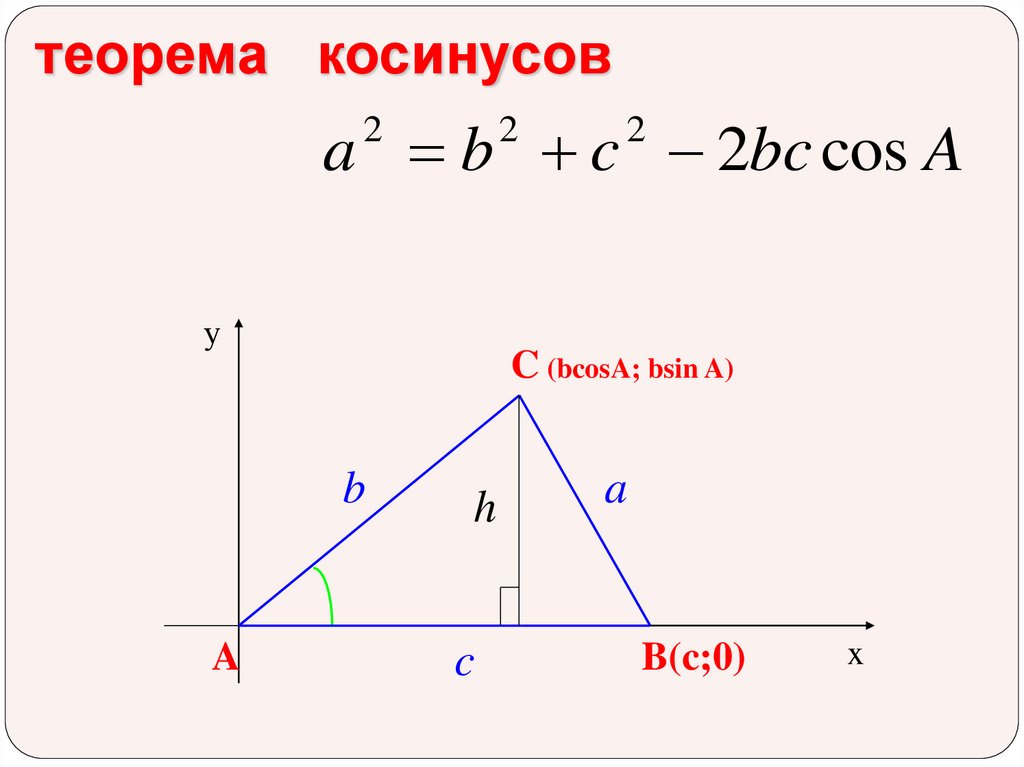
7. теорема косинусов
a b c 2bc cos A2
2
у
C (bcosA; bsin A)
b
A
2
h
c
a
B(c;0)
x
8.
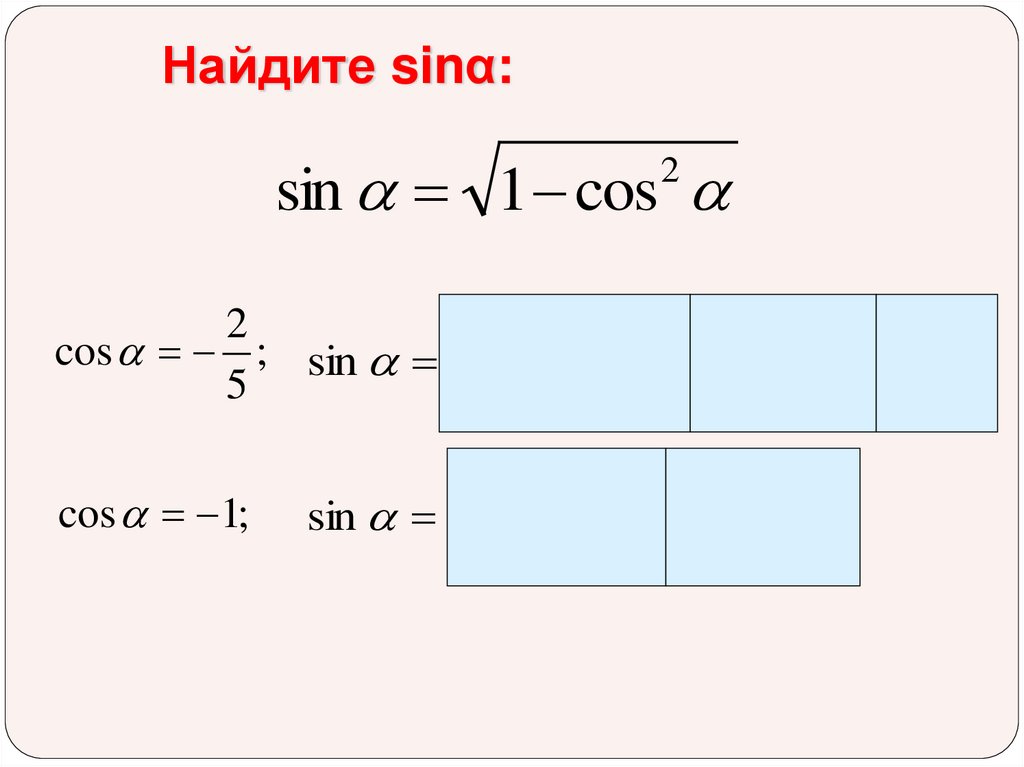
Найдите sinα:sin 1 cos
2
2
cos ; sin 1 ( 2 ) 2 1 4 21
5
5
25
5
cos 1;
sin 1 ( 1) 1 1 0
2
9.
Найдите cosα, если: sin 1 ;4
cos 1 sin
2
1
15
15
cos 1
16
16
4
10.
12
3
4
11.
12
3
12.
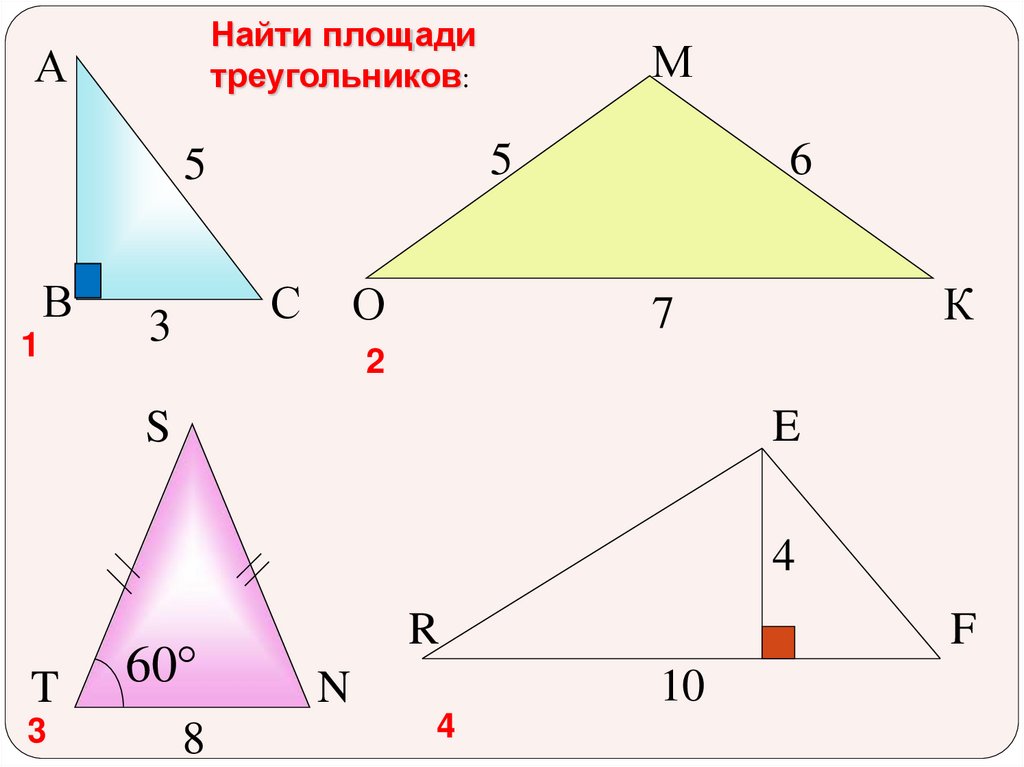
Найти площадитреугольников:
А
5
5
В
1
С
3
М
О
6
К
7
2
E
S
4
T
3
60°
8
R
F
10
N
4
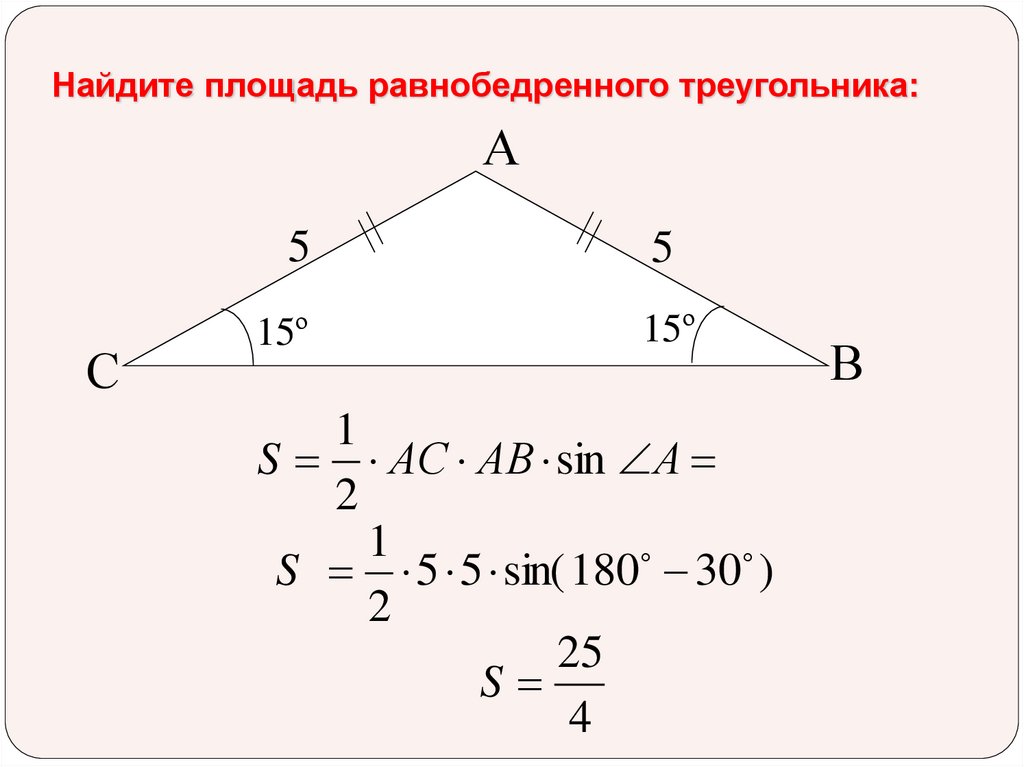
13. Найдите площадь равнобедренного треугольника:
АС
5
5
15º
15º
1
S АС АВ sin А
2
1
S 5 5 sin( 180 30 )
2
25
S
4
В
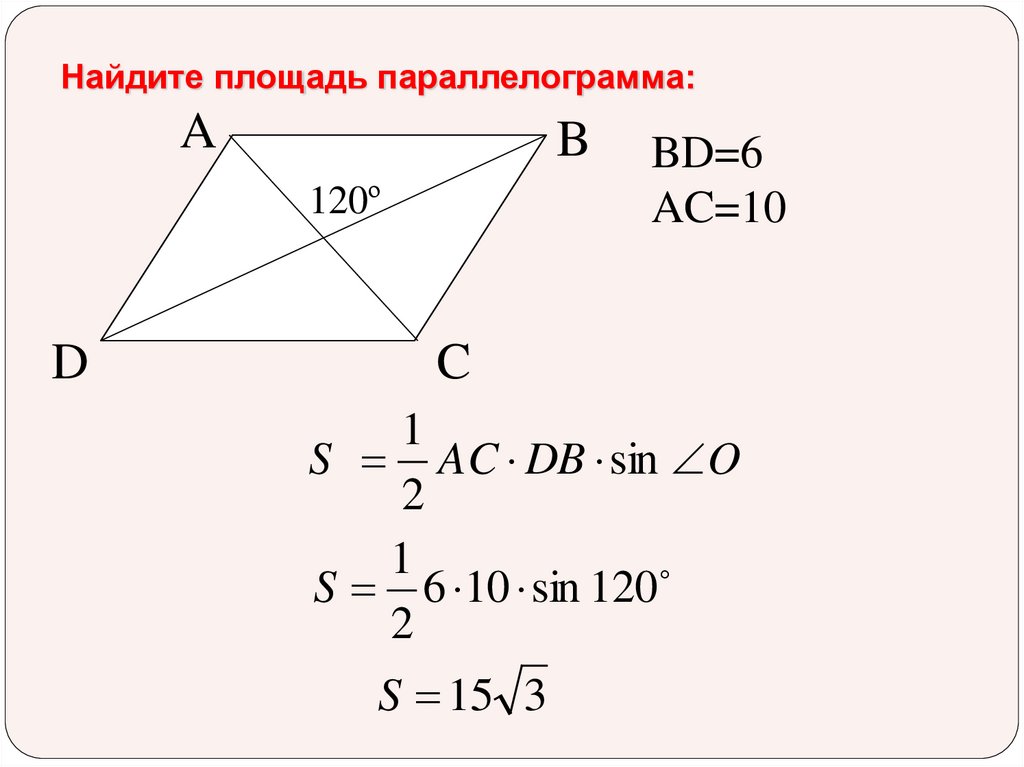
14. Найдите площадь параллелограмма:
AB
120º
D
BD=6
AC=10
C
1
S AC DB sin O
2
1
S 6 10 sin 120
2
S 15 3
15. Найдите площадь параллелограмма:
АВ
45º
5
Д
8
С
S ДА ДС sin Д
S 5 8 sin 45
S 20 2







 mathematics
mathematics








