Плоскость. Определитель плоскости

1.

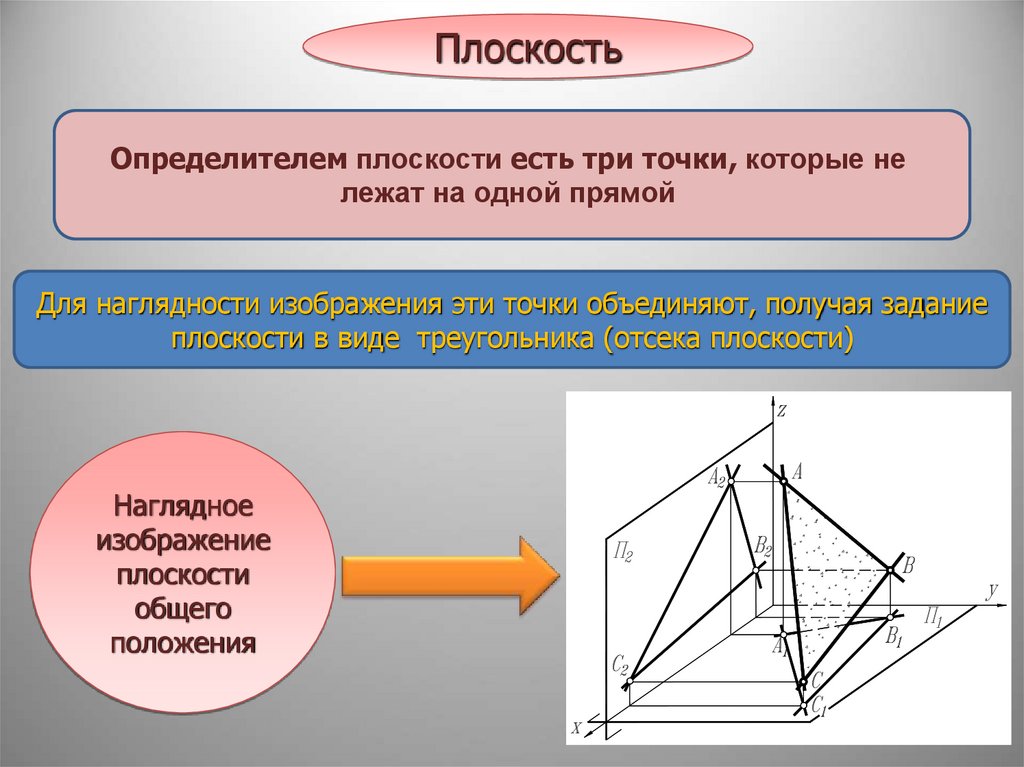
Плоскость
Определителем плоскости есть три точки, которые не
лежат на одной прямой
Для наглядности изображения эти точки объединяют, получая задание
плоскости в виде треугольника (отсека плоскости)
Наглядное
изображение
плоскости
общего
положения

2.

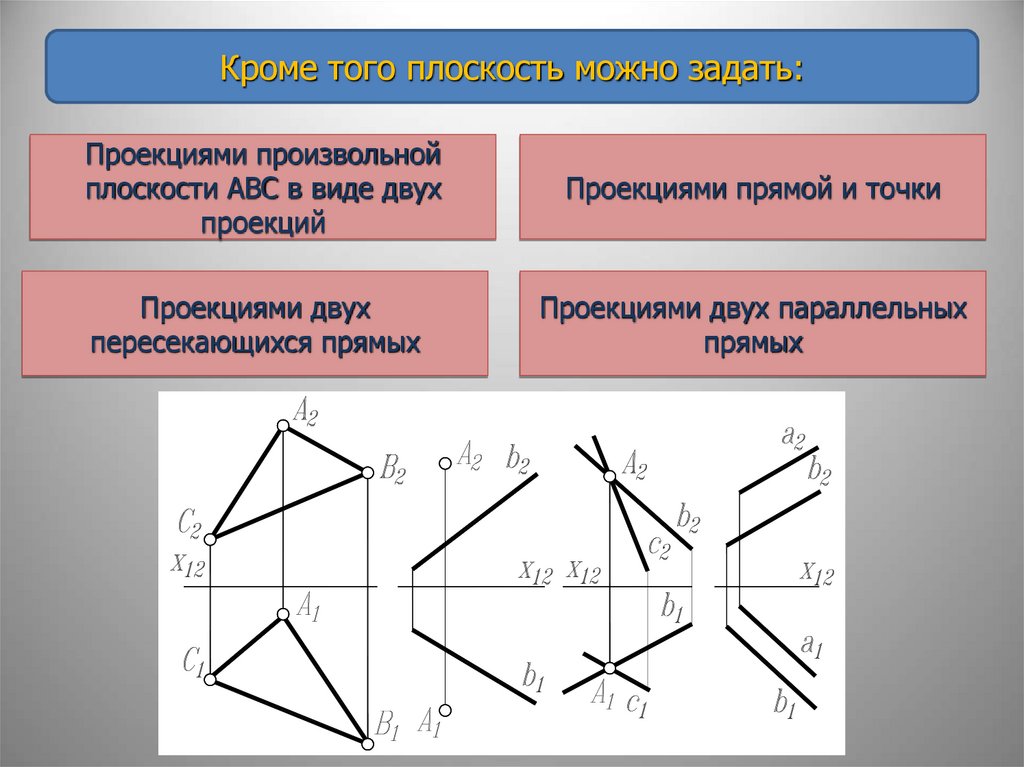
Кроме того плоскость можно задать:
Проекциями произвольной
плоскости АВС в виде двух
проекций
Проекциями прямой и точки
Проекциями двух
пересекающихся прямых
Проекциями двух параллельных
прямых

3.

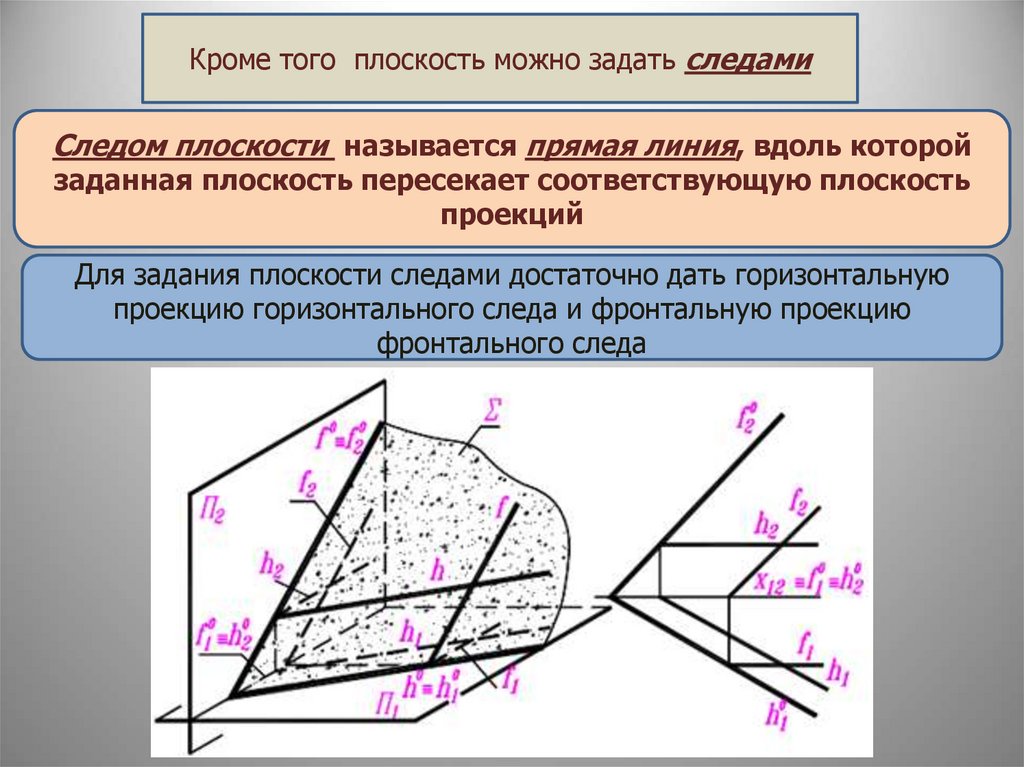
Кроме того плоскость можно задать следами
Следом плоскости называется прямая линия, вдоль которой
заданная плоскость пересекает соответствующую плоскость
проекций
Для задания плоскости следами достаточно дать горизонтальную
проекцию горизонтального следа и фронтальную проекцию
фронтального следа

4.

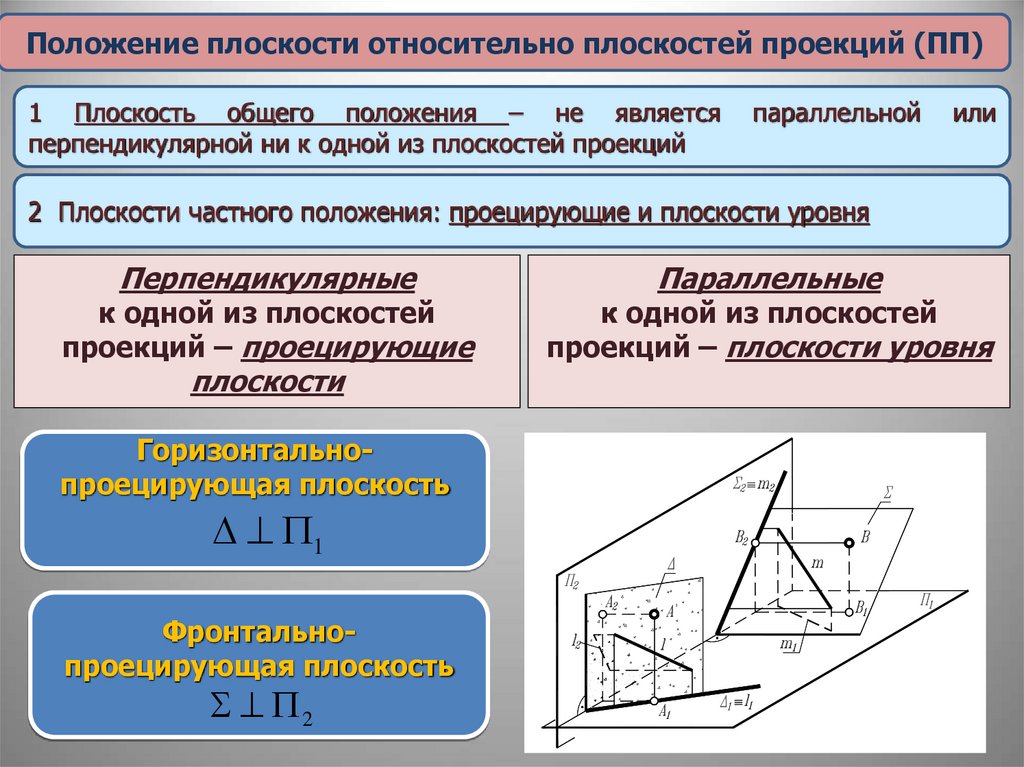
Положение плоскости относительно плоскостей проекций (ПП)
1 Плоскость общего положения – не является
перпендикулярной ни к одной из плоскостей проекций
параллельной
или
2 Плоскости частного положения: проецирующие и плоскости уровня
Перпендикулярные
к одной из плоскостей
проекций – проецирующие
плоскости
Горизонтальнопроецирующая плоскость
1
Фронтальнопроецирующая плоскость
2
Параллельные
к одной из плоскостей
проекций – плоскости уровня

5.

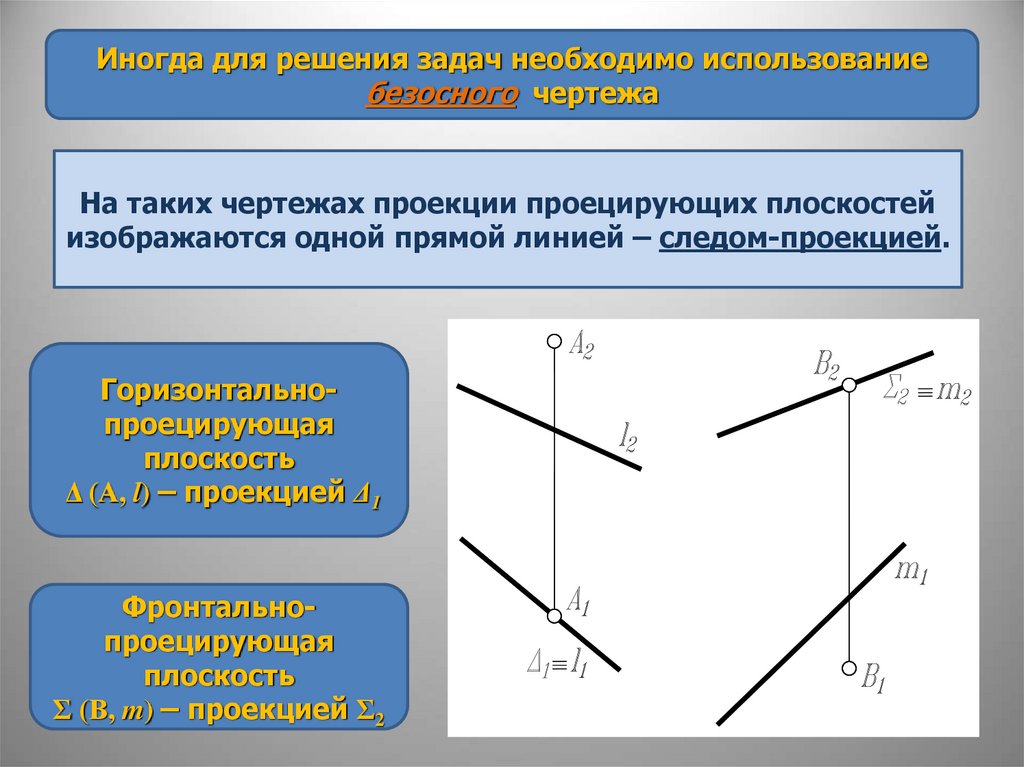
Иногда для решения задач необходимо использование
безосного чертежа
На таких чертежах проекции проецирующих плоскостей
изображаются одной прямой линией – следом-проекцией.
Горизонтальнопроецирующая
плоскость
Δ (А, l) – проекцией Δ1
Фронтальнопроецирующая
плоскость
Σ (В, m) – проекцией Σ2

6.

Плоскости уровня
Горизонтальная плоскость
Фронтальная плоскость
Σ ║ Π1
Δ ║ Π2
Наглядный
чертеж
двух
плоскостей
Комплексный чертеж этих плоскостей
задан единственной проекцией:
горизонтальная плоскость – проекцией Σ2 ;
фронтальная – проекцией Δ1.

7.

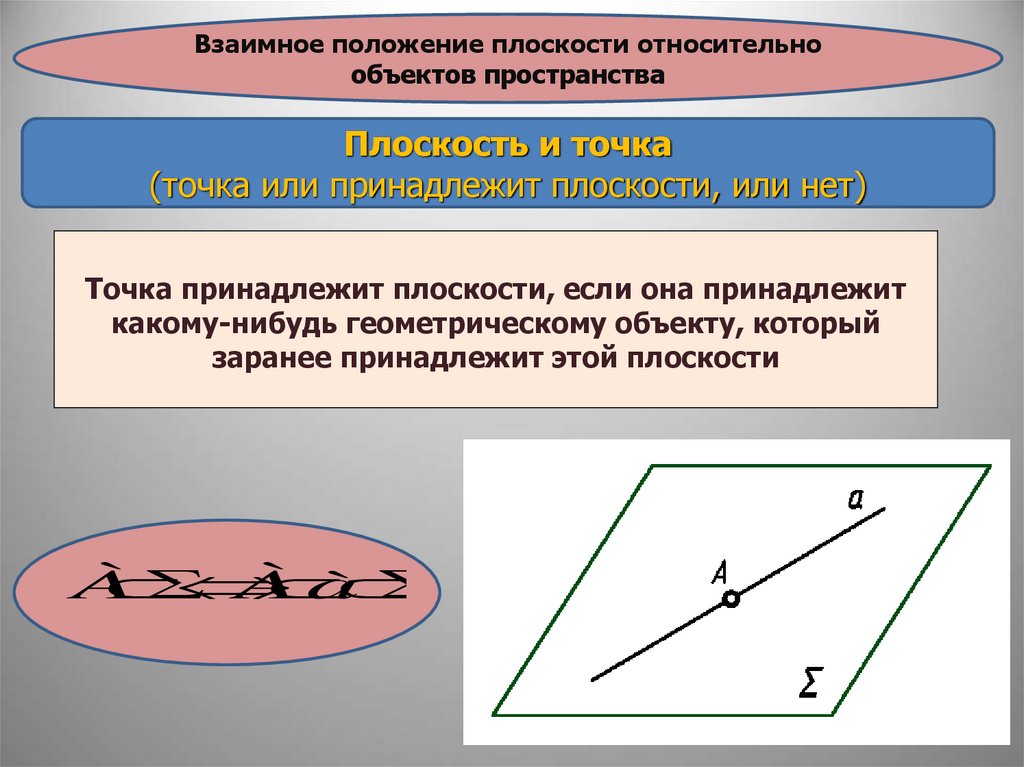
Взаимное положение плоскости относительно
объектов пространства
Плоскость и точка
(точка или принадлежит плоскости, или нет)
Точка принадлежит плоскости, если она принадлежит
какому-нибудь геометрическому объекту, который
заранее принадлежит этой плоскости
À
À
à

8.

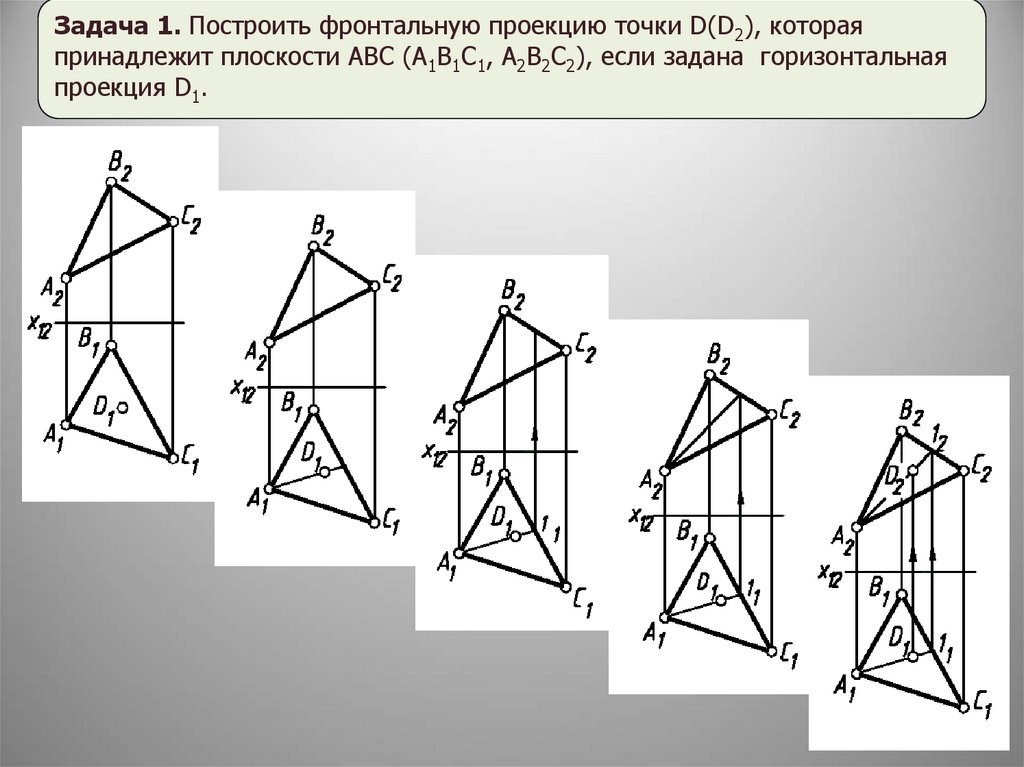
Задача 1. Построить фронтальную проекцию точки D(D2), которая
принадлежит плоскости АВС (А1В1С1, А2В2С2), если задана горизонтальная
проекция D1.

9.

Главные линии плоскости – линии уровня
Главные линии плоскости это линии, которые соответствуют двум
условиям:
1) принадлежат данной плоскости;
2) параллельны одной из плоскостей проекций
Горизонталь – прямая, которая
принадлежит плоскости и является
параллельной горизонтальной плоскости
проекций
h (ABC) и h II Π1
Построение горизонтали начинают с
построения фронтальной ее
проекции, при этом
h2 II x12

10.

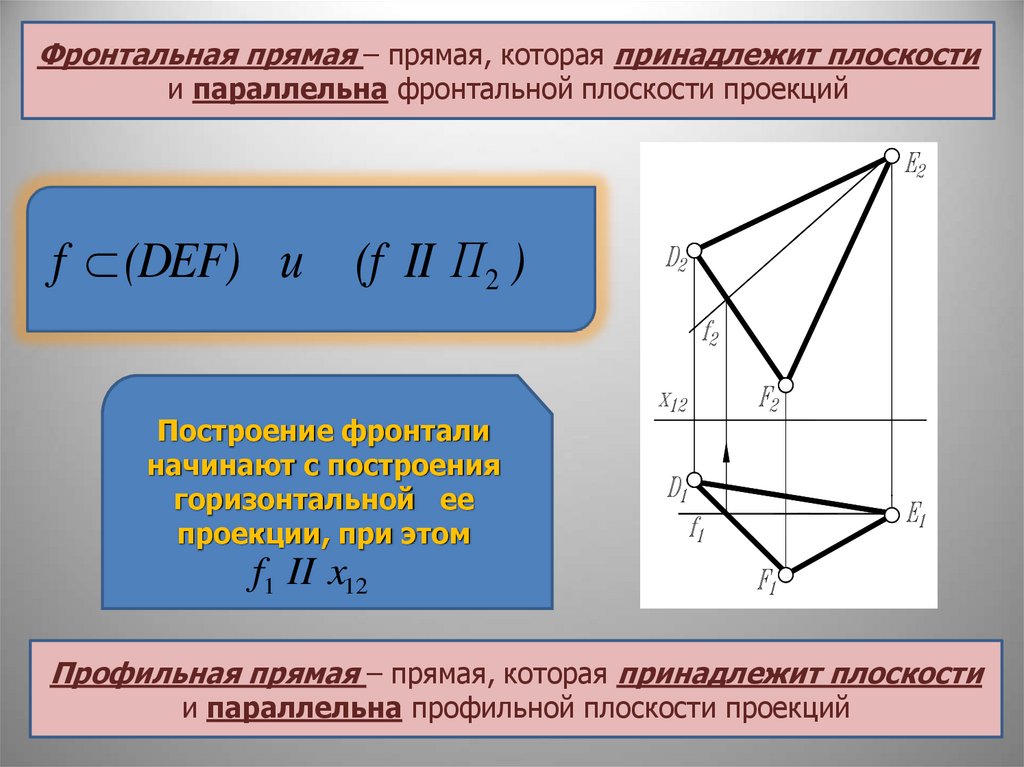
Фронтальная прямая – прямая, которая принадлежит плоскости
и параллельна фронтальной плоскости проекций
f (DEF) и
(f II Π2 )
Построение фронтали
начинают с построения
горизонтальной ее
проекции, при этом
f1 II x12
Профильная прямая – прямая, которая принадлежит плоскости
и параллельна профильной плоскости проекций

11.

Линии наибольшего наклона плоскости
к плоскостям проекций
Линии наибольшего наклона плоскости к
горизонтальной плоскости проекций называют
линией наибольшего ската
Линией наибольшего наклона плоскости к плоскостям
проекций (П1 и П2) называют прямую, лежащую в плоскости
и перпендикулярную соответственно или к горизонталям или
к фронталям этой плоскости
На основании свойства параллельного проецирования о
взаимной перпендикулярности прямых линий устанавливаем, что
прямой угол, составленный горизонталью с линией
наибольшего наклона, проецируется на эту плоскость
без искажения

12.

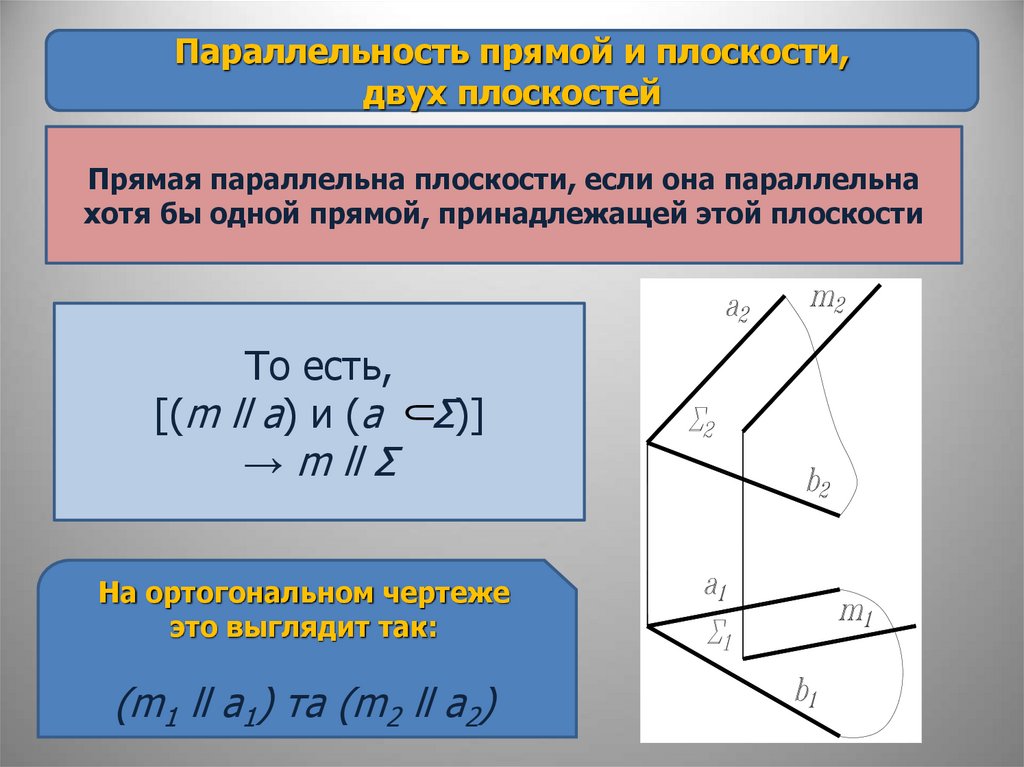
Параллельность прямой и плоскости,
двух плоскостей
Прямая параллельна плоскости, если она параллельна
хотя бы одной прямой, принадлежащей этой плоскости
То есть,
[(m ll a) и (a Σ)]
→ m ll Σ
На ортогональном чертеже
это выглядит так:
(m1 ll a1) та (m2 ll a2)

13.

Две плоскости параллельны, если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой плоскости
[Σ (a ∩ b) и Δ (m ∩ n)]
и [(m ll a) и (n ll b)]
→ Σ ll Δ

14.

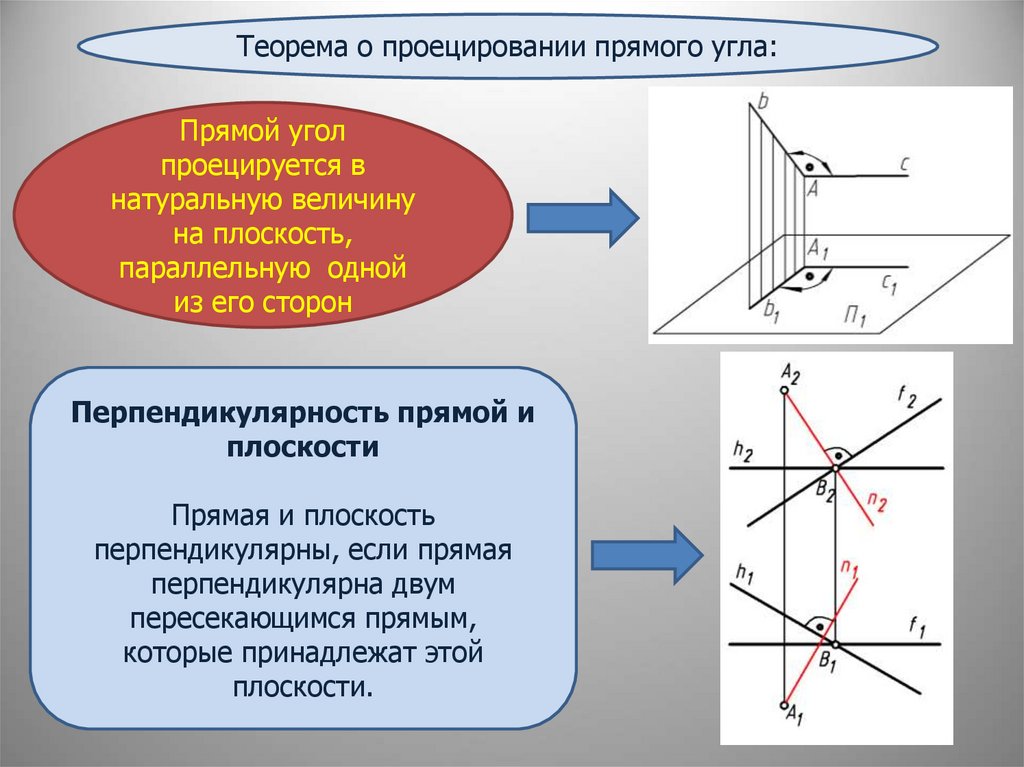
Теорема о проецировании прямого угла:
Прямой угол
проецируется в
натуральную величину
на плоскость,
параллельную одной
из его сторон
Перпендикулярность прямой и
плоскости
Прямая и плоскость
перпендикулярны, если прямая
перпендикулярна двум
пересекающимся прямым,
которые принадлежат этой
плоскости.

15.

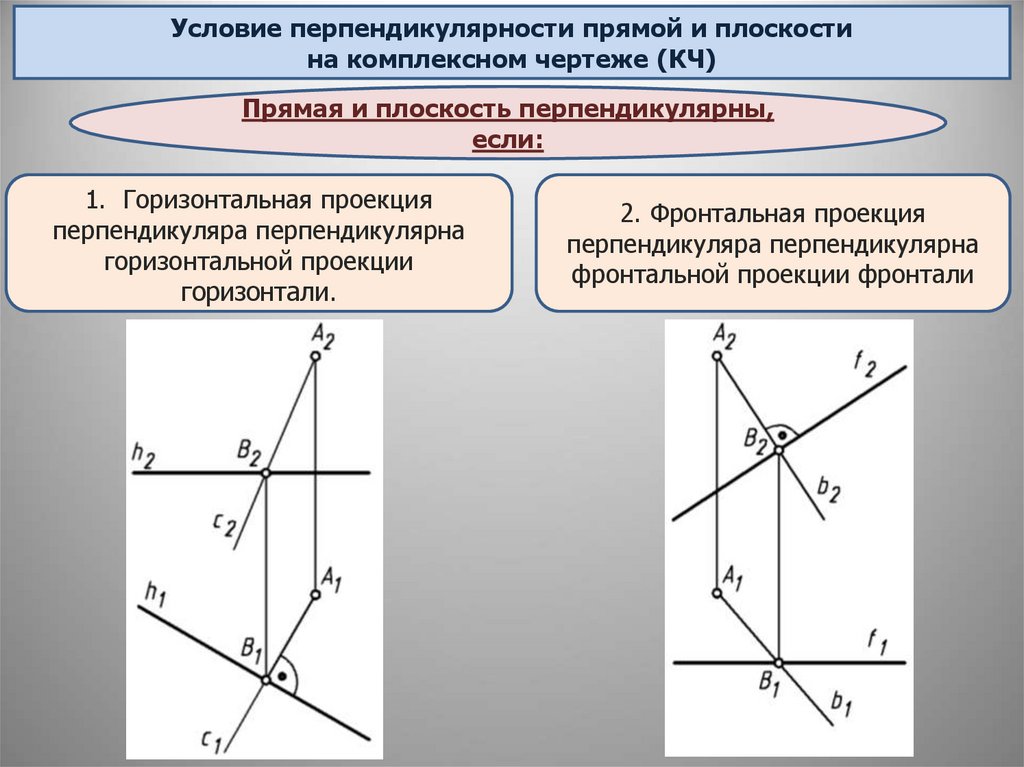
Условие перпендикулярности прямой и плоскости
на комплексном чертеже (КЧ)
Прямая и плоскость перпендикулярны,
если:
1. Горизонтальная проекция
перпендикуляра перпендикулярна
горизонтальной проекции
горизонтали.
2. Фронтальная проекция
перпендикуляра перпендикулярна
фронтальной проекции фронтали

16.

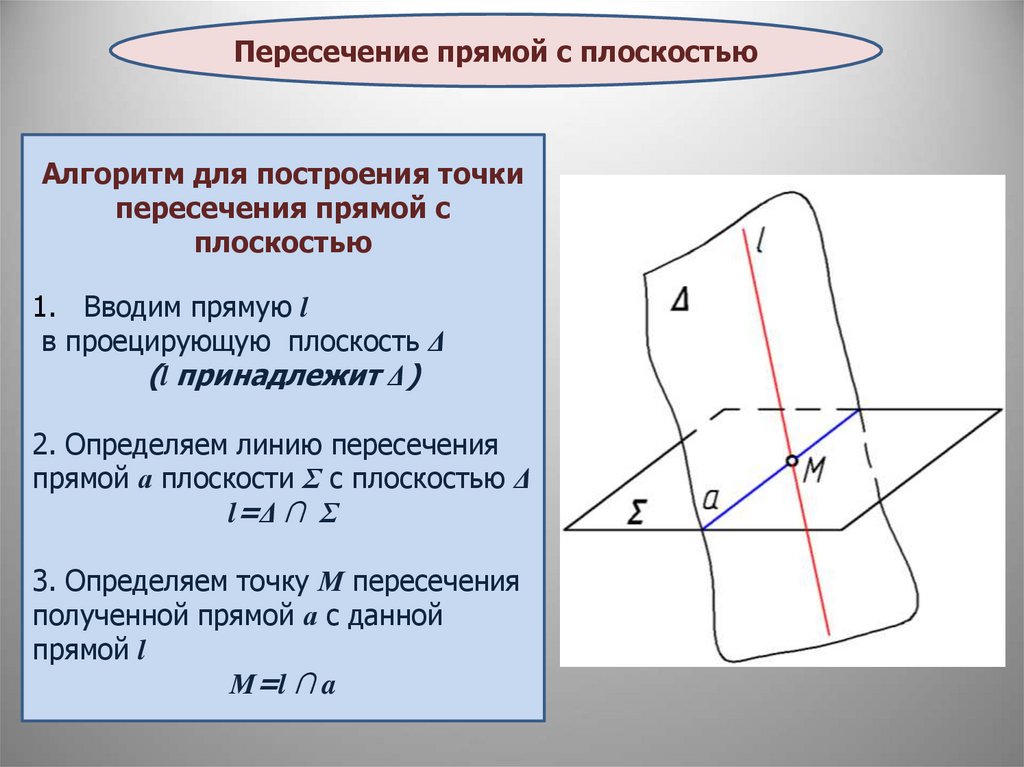
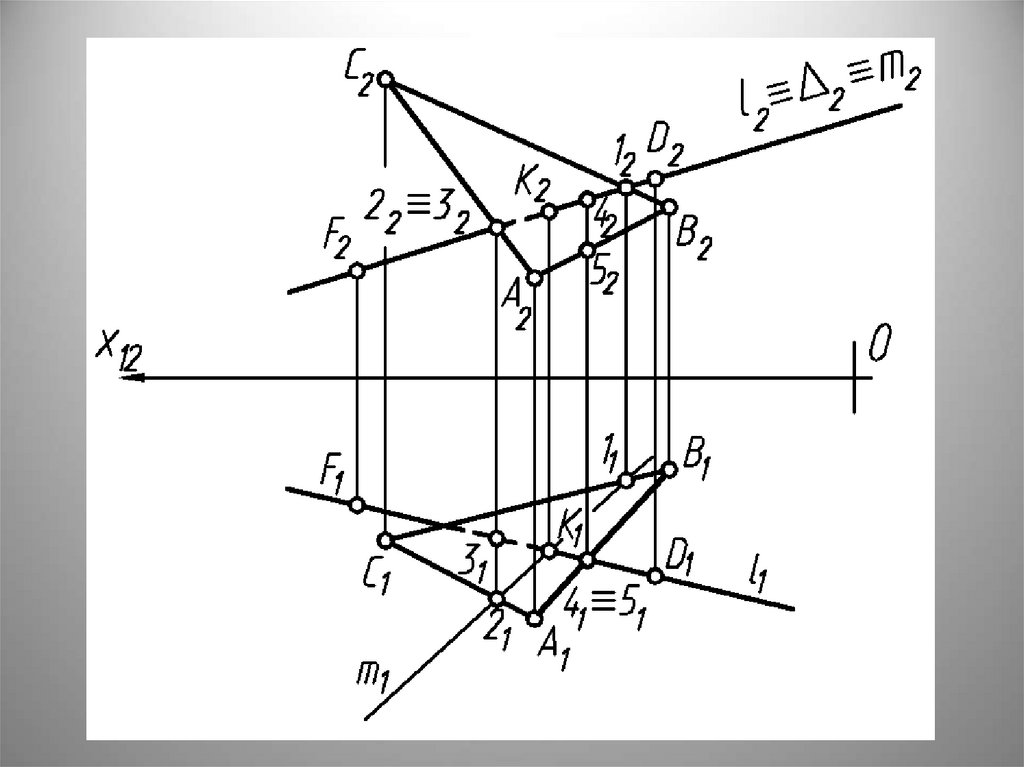
Пересечение прямой с плоскостью
Алгоритм для построения точки
пересечения прямой с
плоскостью
1. Вводим прямую l
в проецирующую плоскость Δ
(l принадлежит Δ)
2. Определяем линию пересечения
прямой а плоскости Σ с плоскостью Δ
l=Δ ∩ Σ
3. Определяем точку М пересечения
полученной прямой а с данной
прямой l
М=l ∩ a

17.

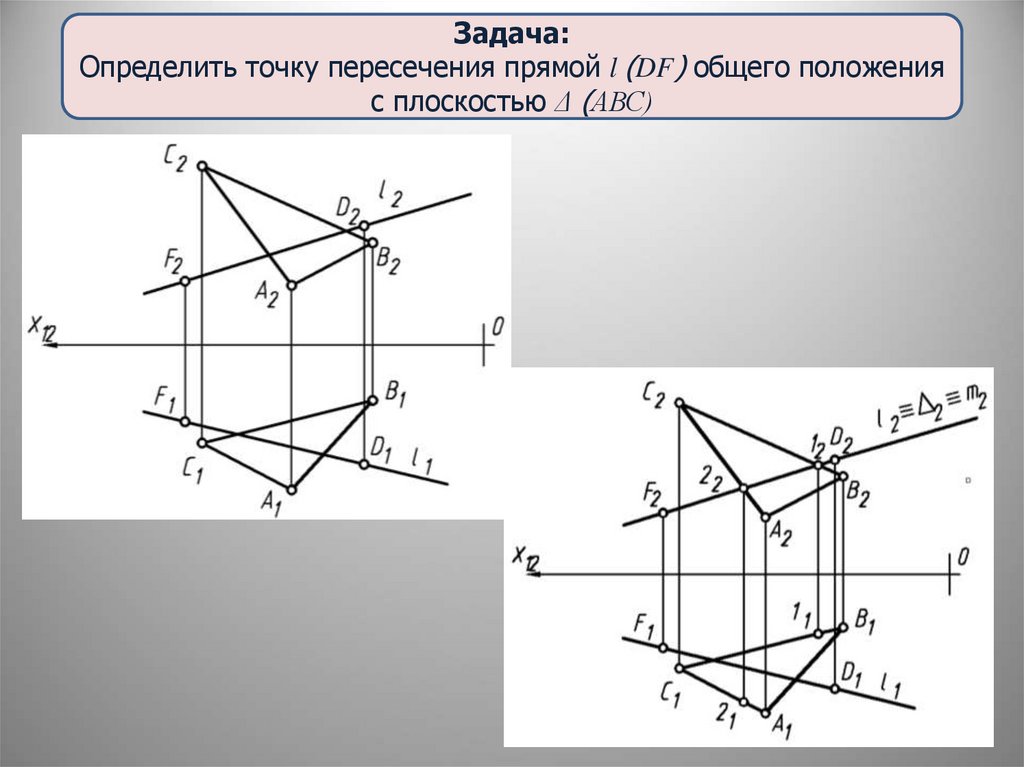
Задача:
Определить точку пересечения прямой l (DF) общего положения
с плоскостью Δ (АВС)