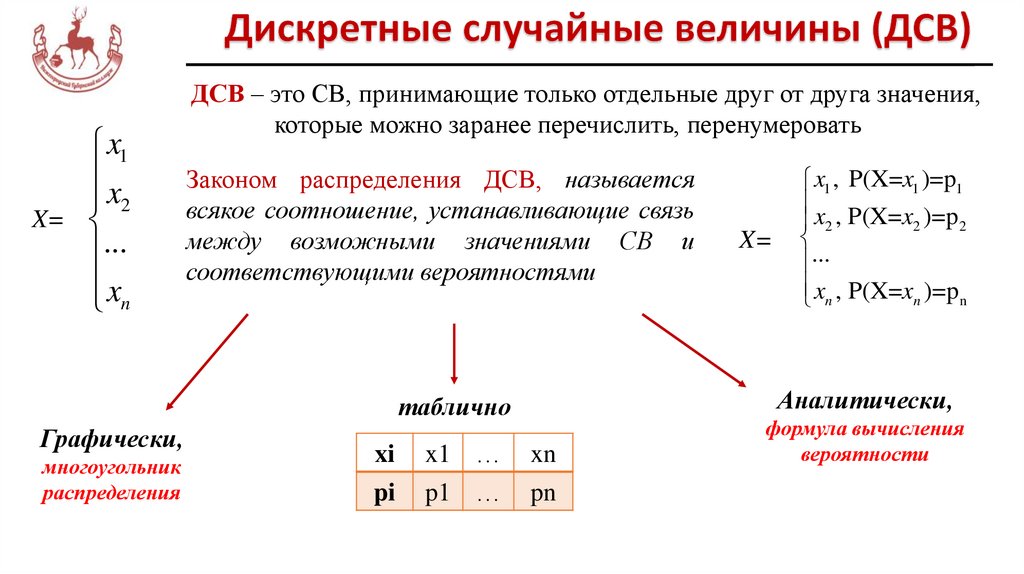
Дискретные случайные величины (ДВС)

1.

X=
x1
x
2
...
xn
ДСВ – это СВ, принимающие только отдельные друг от друга значения,
которые можно заранее перечислить, перенумеровать
Законом распределения ДСВ, называется
всякое соотношение, устанавливающие связь
между возможными значениями СВ и
соответствующими вероятностями
Аналитически,
таблично
Графически,
многоугольник
распределения
xi
pi
x1 …
p1 …
X=
x1 , P(X=x1 )=p1
x , P(X=x )=p
2
2
2
...
xn , P(X=xn )=p n
xn
pn
формула вычисления
вероятности

2.

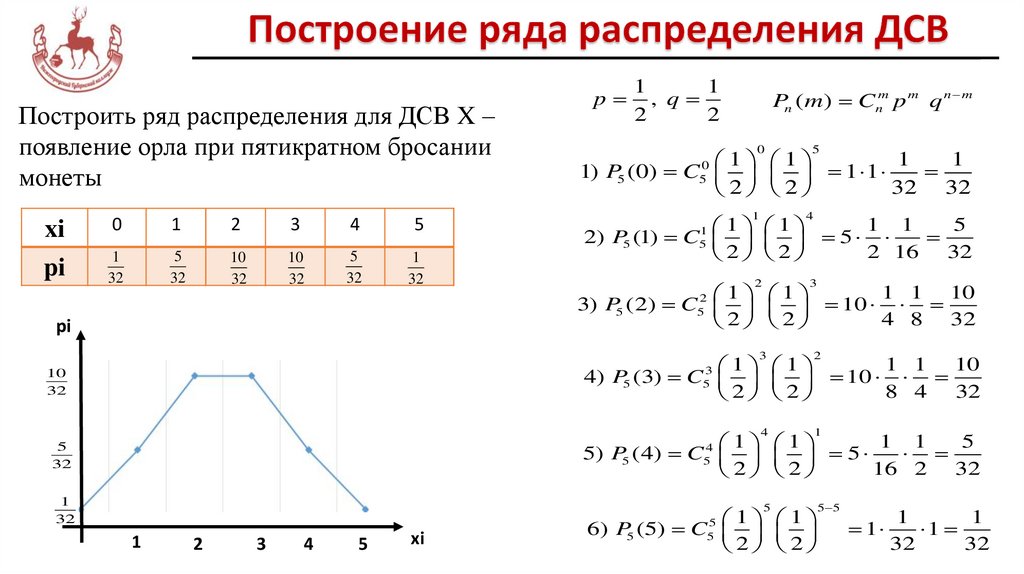
Построить ряд распределения для ДСВ X –
появление орла при пятикратном бросании
монеты
xi
pi
0
1
2
3
4
5
1
32
5
32
10
32
10
32
5
32
1
32
p
1
1
, q
2
2
Pn ( m) Cnm p m q n m
0
5
1
4
2
3
3
2
4
1
5
5 5
1
1
1 1
1) P5 (0) C 1 1
32 32
2 2
0
5
1 1
5
1 1
2) P5 (1) C51 5
2 16 32
2 2
1 1 10
1 1
3) P5 (2) C 10
4 8 32
2 2
2
5
pi
10
32
1 1 10
1 1
4) P5 (3) C 10
8 4 32
2 2
5
32
1 1
5
1 1
5) P5 (4) C 5
16 2 32
2 2
3
5
4
5
1
32
1
2
3
4
5
xi
1 1
6) P5 (5) C55
2 2
1
1
1
1
32
32

3.

ФР F(x) называют функцию, которая для каждого значения x определяет
вероятность того, что СВ Х примет значение меньше x:
F(x)=P(X<x), где x-текущие значение СВ.
x1
…
xn
x
Свойства функции распределения:
1.
2.
3.
4.
5.
F(x) – неубывающая функция своего аргумента.
F(-∞)=0
F(+∞)=1
Все значения F(x) принадлежат отрезку [0;1], т.е. 0≤F(x)≤1
Если все возможные значения СВ Х принадлежат интервалу (а;b), то ее
F(x) будет равна F(x)=0 при х≤а и F(x)=1 при х≥b

4.

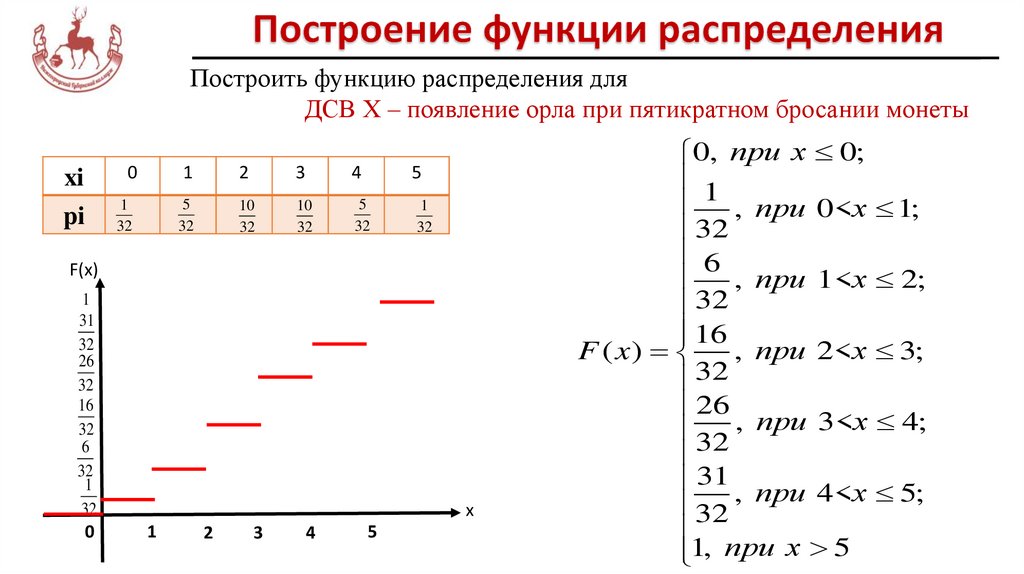
Построить функцию распределения для
ДСВ Х – появление орла при пятикратном бросании монеты
xi
pi
0
1
2
3
4
5
1
32
5
32
10
32
10
32
5
32
1
32
1) x 0
F ( x) P ( X 0) 0
F ( x) P ( X 4) P ( X 2)
3 P ( X 3)
16 10 26
32 32 32
6) 4<x 5
F ( x) P ( X 5) P ( X 3)
4 P ( X 4)
2) 0<x 1
F ( x) P ( X 1) P ( X 0)
5) 3<x 4
26
5
31
32 32 32
7) x>5
1
32
F ( x) P ( X ) P ( X 4)
5 P ( X 5)
3) 1<x 2
F ( x) P ( X 2) P ( X 0) P ( X 1)
1
5
6
32 32 32
4) 2<x 3
F ( x) P ( X 3) P ( X 0) P ( X 1) P ( X 2)
1
5
10 16
32 32 32 32
31
1
32
1
32 32 32

5.

Построить функцию распределения для
ДСВ Х – появление орла при пятикратном бросании монеты
xi
pi
0
1
2
3
4
5
1
32
5
32
10
32
10
32
5
32
1
32
F(x)
1
31
32
26
32
16
32
6
32
1
32
0
x
1
2
3
4
5
0, при x 0;
1
, при 0<x 1;
32
6
, при 1<x 2;
32
16
F ( x)
, при 2<x 3;
32
26
32 , при 3<x 4;
31 , при 4<x 5;
32
1, при x 5

6.

Мода (Mo) – значение ДСВ имеющие максимальную вероятность;
Медиана (Ме) – значение ДСВ, для которого вероятность попасть справа и слева от
нее одинакова;
Математическое ожидание М(х) – сумма произведений возможных значений СВ
на соответствующие вероятности;
Дисперсия D(х) – характеристика рассеяния, разброса значений СВ относительно
математического ожидания;
Среднее квадратическое отклонение (x) – стандартное отклонение СВ от
математического ожидания
n
М ( х) xi pi
i 1
D( х) M ( x ) M ( x)
2
2
( х) D( x)

7.

ДСВ Х – появление орла при пятикратном бросании монеты
0
xi
pi
1
32
1
2
3
4
5
5
32
10
32
10
32
5
32
1
32
1) Mo = 2,3 2) Me = 2,3
6
1
5
10
10
5
1 80
3) М ( х) xi pi 0 1 2 3 4 5
=2,5
32
32
32
32
32
32 32
i 1
6
1
5
10
10
5
1 240
2
2
4) М ( х ) ( xi ) pi 0 1 4 9 16 25
=7,5
32
32
32
32
32
32 32
i 1
240 6400 7680 6400 1280
5) D( х) M ( x ) M ( x)
=1,25
32 1024 1024 1024 1024
2
2
1280
6) ( х) D( x)
=1,12
1024