Урок 10. Случайные величины. Дискретные и непрерывные случайные величины (ДСВ и НСВ)

1. Раздел 2. Теория случайных величин.

Урок 10. Случайные величины.
Дискретные и непрерывные
случайные величины (ДСВ и НСВ).

2. Определения.

Случайной величиной называется величина,
которая в результате опыта может принять то
или иное возможное значение, неизвестное
заранее, но обязательно одно.
Например: Количество билетов в кассе на
определенное число; число бракованных
изделий в партии из 10 деталей; число
выпавших «гербов» при пятикратном
бросании монеты и т.д.

3. Определения.

Дискретной случайной величиной (ДСВ)
называют такую случайную величину,
множество возможных значений которой
конечное или бесконечное, но счетное
множество.
Непрерывной случайной величиной (НСВ)
называют такую случайную величину,
множество возможных значений которой есть
конечный или бесконечный интервал.
Например: Диаметр трубы; дальность полета
снаряда; температура воздуха и т.д.

4. Обозначения: X;Y;Z – случайные величины; x;y;z – их возможные значения.

Например: X – количество шахматных партий,
окончившихся вничью при трех сыгранных.
х1=0; х2=1; х3=2; х4=3.

5. Операции над ДСВ.

Суммой X+Y ДСВ называется величина Z,
возможные значения которой есть суммы
возможных значений этих величин.
Произведением X*Y называется величина Z,
возможные значения которой есть
произведения возможных значений этих
величин.
Аналогично: X-Y; X/Y

6.

Например: X - количество шахматных партий,
окончившихся вничью при трех сыгранных.
Y – количество очков при бросании игральной
кости.
х1=0; х2=1; х3=2; х4=3.
y1=1; y2=2; y3=3; y4=4, y5=5; y6=6;
Z=X+Y: z1=1; z2=2; z3=3; z4=4, z5=5; z6=6;
z7=7; z8=8; z9=9;
Z=X*Y: z1=0; z2=1; z3=2; z4=3, z5=4; z6=5;
z7=6; z8=8; z9=10; z10=12; z11=9; z12=15;
z13=18;

7. Распределение вероятностей случайных величин.

Появление тех или иных случайных величин
можно рассматривать как событие, а
различным событиям соответствуют
различные вероятности. Поэтому возможные
значения случайной величины отличаются с
вероятностной точки зрения.
Например: Пусть брошены две игральные кости.
Z=X+Y: z1=2; z2=8; P(z1)=1/36; P(z2)=5/36

8. Закон распределения ДСВ.

Пусть Х – ДСВ, возможные значения которой:
х1; х2; х3;… ;хn.
Обозначим вероятности этих событий:
Р(Х=х1); Р(Х=х2); Р(Х=х3);…;Р(Х=хn)
Законом распределения ДСВ называется
всякое соответствие, устанавливающее связь
между значением случайной величины и
соответствующими вероятностями.

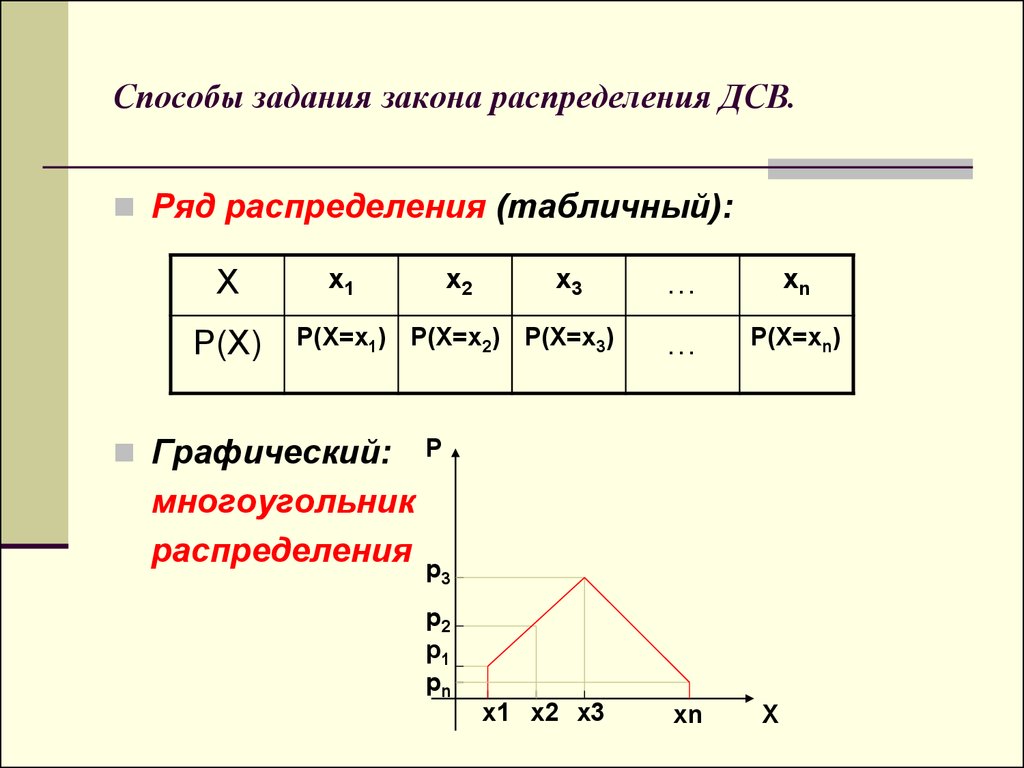
9. Способы задания закона распределения ДСВ.

Ряд распределения (табличный):
Х
Р(Х)
х1
х2
х3
Р(Х=х1) Р(Х=х2) Р(Х=х3)
Графический:
многоугольник
распределения
…
хn
…
Р(Х=хn)
Р
р3
р2
р1
рn
х1 х2 х3
хn
Х

10. Задача 1.

1.
2.
3.
4.
5.
В партии из 8 деталей 5 стандартных. Наудачу взяты 4
детали. Построить ряд распределения числа
стандартных деталей среди отобранных.
Алгоритм построения ряда распределения:
Построить пространство элементарных исходов (поле
значений СВ);
Вычислить вероятности появления каждого значения
СВ;
Построить ряд распределения (таблицу
соответствий);
Выполнить проверку: р1+ р2+ р3+…+ рn=1
При необходимости построить многоугольник
распределения.

11. Задача 2.

Стрелок, имея 4 патрона, стреляет до первого
попадания в цель. Вероятность попадания при
одном выстреле – 0,6. Построить ряд
распределения числа используемых
патронов.

12. Задача 2.

Составить ряд распределения числа
выпавших очков при бросании двух
игральных костей.
Построить многоугольник
распределения.