Similar presentations:
Дискретные случайные величины. Основные законы распределения дискретных случайных величин
1.
Дискретные случайныевеличины.
Основные законы
распределения дискретных
случайных величин.
2.
Основные понятияСлучайной называют величину, принимающую в
результате испытаний те или иные возможные
значения, наперед неизвестные и зависящие от
случайных причин, которые заранее не могут быть
учтены.
Принятие
случайной
величиной
некоторого
числового значения X=xi есть случайное событие,
характеризуемое вероятностью P(X=xi) = pi .
3.
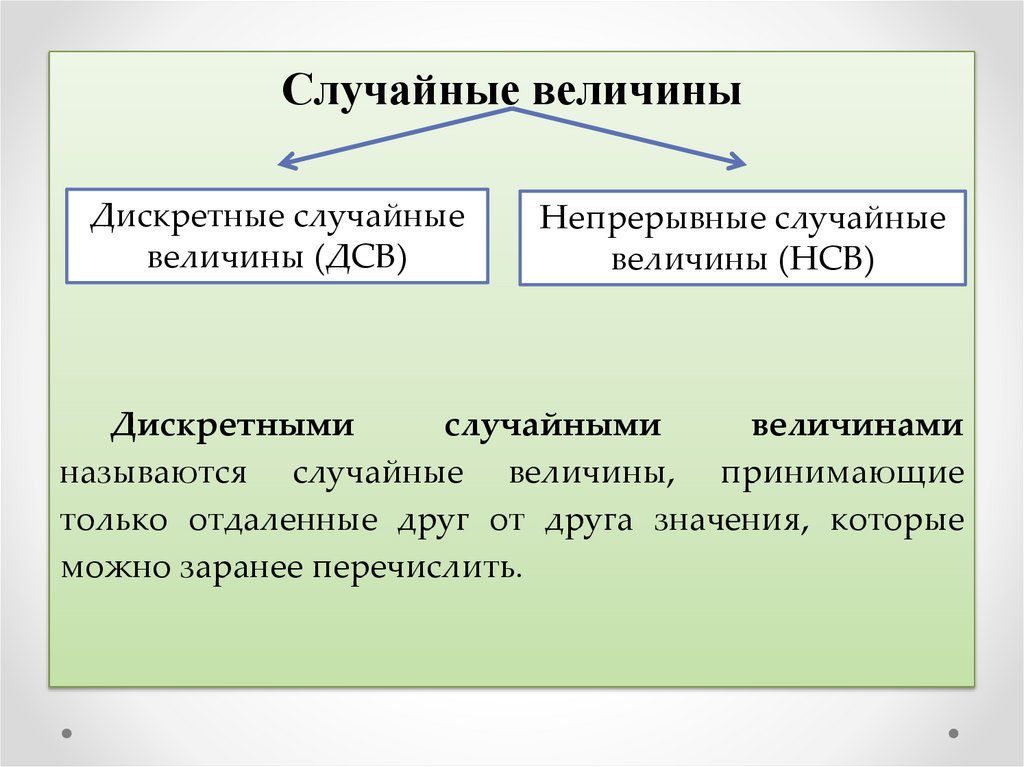
Случайные величиныДискретные случайные
величины (ДСВ)
Непрерывные случайные
величины (НСВ)
Дискретными
случайными
величинами
называются случайные величины, принимающие
только отдаленные друг от друга значения, которые
можно заранее перечислить.
4.
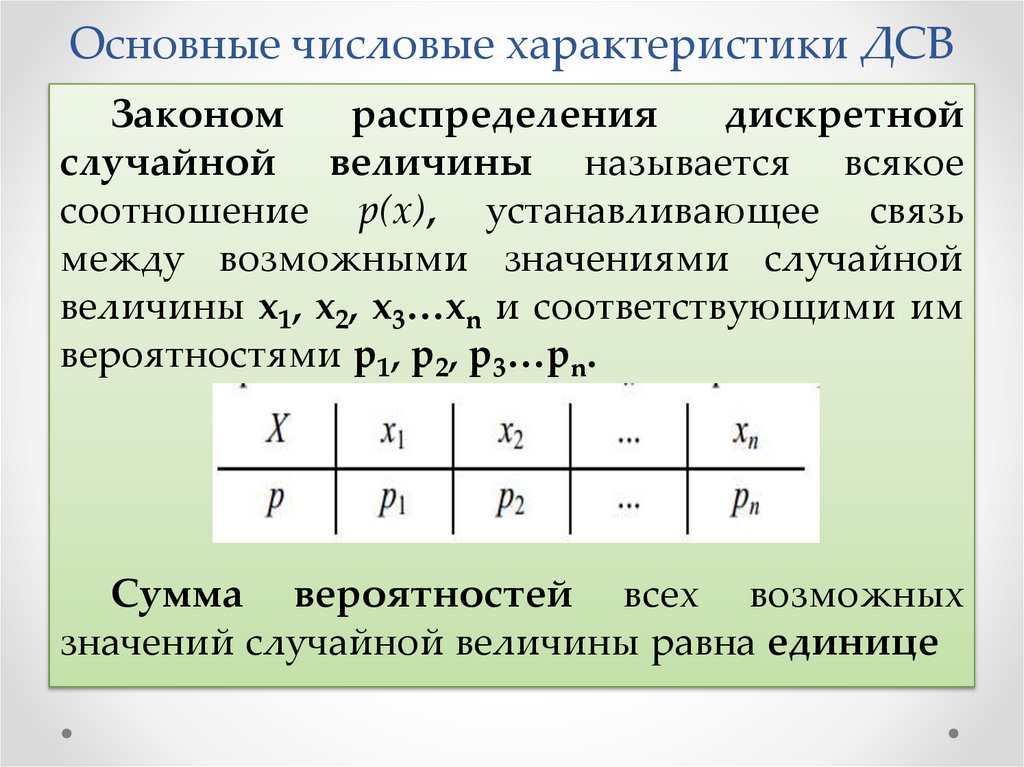
Основные числовые характеристики ДСВЗаконом
распределения
дискретной
случайной величины называется всякое
соотношение p(x), устанавливающее связь
между возможными значениями случайной
величины x1, x2, x3…xn и соответствующими им
вероятностями p1, p2, p3…pn.
Сумма вероятностей всех возможных
значений случайной величины равна единице
5.
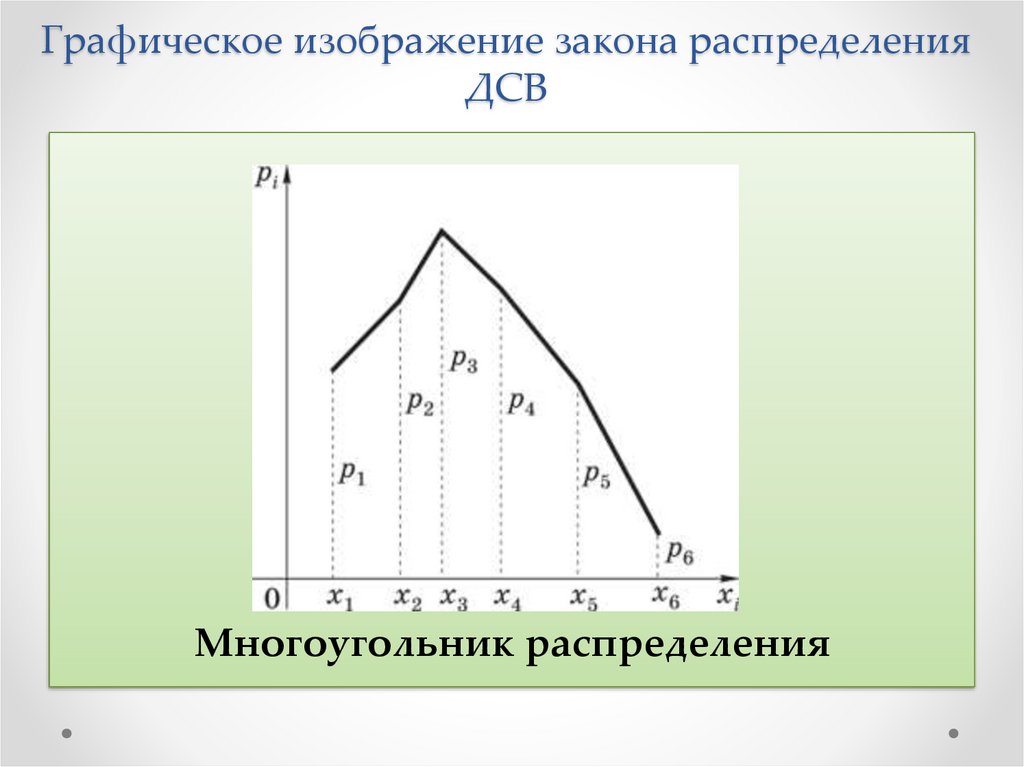
Графическое изображение закона распределенияДСВ
Многоугольник распределения
6.
ПримерВ коробке находятся 50 лотерейных билетов, среди
которых 12 выигрышных, причём 2 из них выигрывают
по 1000 рублей, а остальные – по 100 рублей. Составить
закон распределения случайной величины Х – размера
выигрыша, если из коробки наугад извлекается один
билет.
Решение:
х1=0 рублей
х2=100 рублей
х3=1000
7.
ПримерПроверка:
Закон распределения ДСВ Х:
8.
ПримерОхотник, имеющий 4 патрона, стреляет по дичи до
первого попадания или расходования всех патронов.
Вероятность попадания при первом выстреле равна 0,7,
при каждом следующем выстреле уменьшается на 0,1.
Составить закон распределения числа патронов,
израсходованных охотником.
случайная величина X – число патронов,
израсходованных охотником
Х=1,2,3,4
Событие Аi - попадание при i – ом выстреле
Событие Аi – промах при i – ом выстреле
9.
ПримерP(A1)=0,7
P(A1)=1-0,7=0,3
P(A2)=0,6
P(A2)=1-0,6=0,4
P(A3)=0,5
P(A3)=1-0,5=0,5
P(A4)=0,4
P(A4)=1-0,4=0,6
охотник попал
в
цель
с
охотник
в
цель
со
первого выстрела
попал
второго выстрела
охотник попал в цель с
третьего выстрела
10.
Примерохотник попал в цель с четвертого выстрела либо
промахнулся все четыре раза
Проверка:
xi
pi
1
0,7
2
0,18
3
0,06
4
0,06
11.
Задачи12.
Задача 1. Вероятность того, что стрелок поразитмишень, равна 0,7. Составить закон распределения
случайной величины Х – количества попаданий после 2
выстрелов.
Задача 2. Рабочий обслуживает три станка. Вероятность
того, что в течение часа первый станок не потребует
регулировки – 0,9, второй – 0,8, третий – 0,7. Составить
закон распределения числа станков, которые в течение
часа потребуют регулировки.
13.
Функцияраспределения
14.
Основные понятияФункцией распределения называют функцию
F(x), определяющую вероятность того, что случайная
величина X в результате испытания примет значение,
меньшее некоторого фиксированного значения x.
15.
Свойства функции распределения1.
2. F(x) - неубывающая функция, т.е.
, если
3.
4. F(x) непрерывна слева в любой точке x, т.е.
5.
Функция распределения ДСВ имеет вид
где суммирование ведется по всем индексам i, для
которых
16.
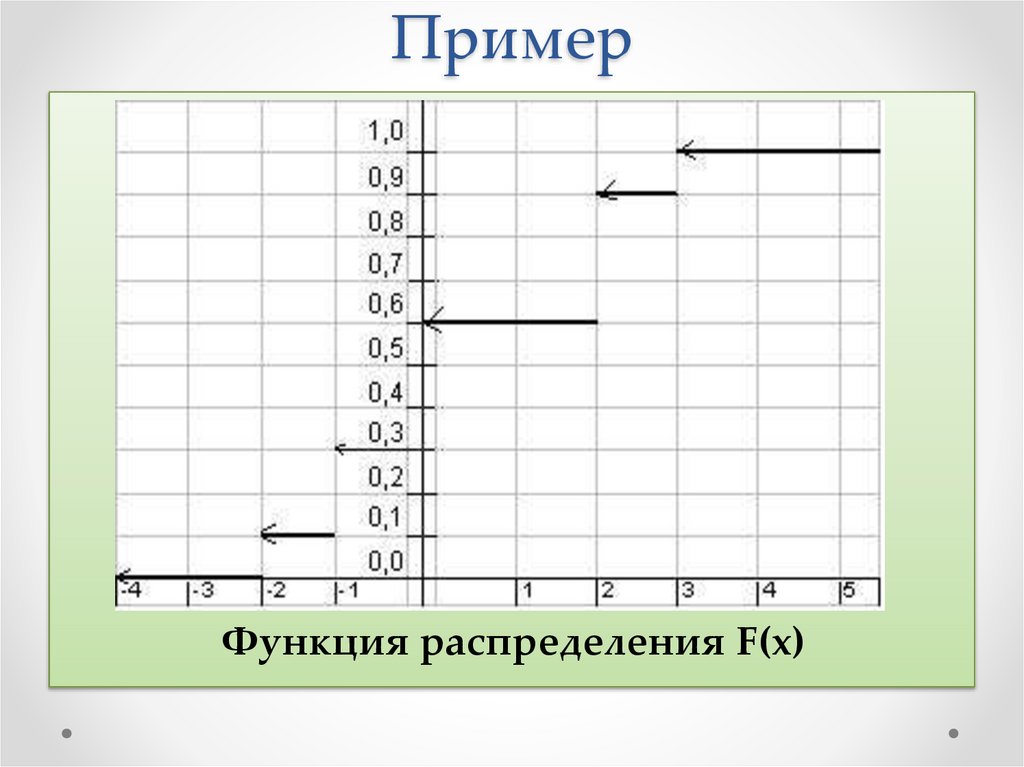
ПримерЗадан закон распределения ДСВ Х
Xi
pi
-2
0,1
-1
0,2
0
0,3
2
0,3
3
0,1
Найти функцию распределения и построить ее
график.
17.
Пример18.
ПримерФункция распределения F(x)














 mathematics
mathematics








