§6. Векторная алгебра

1.

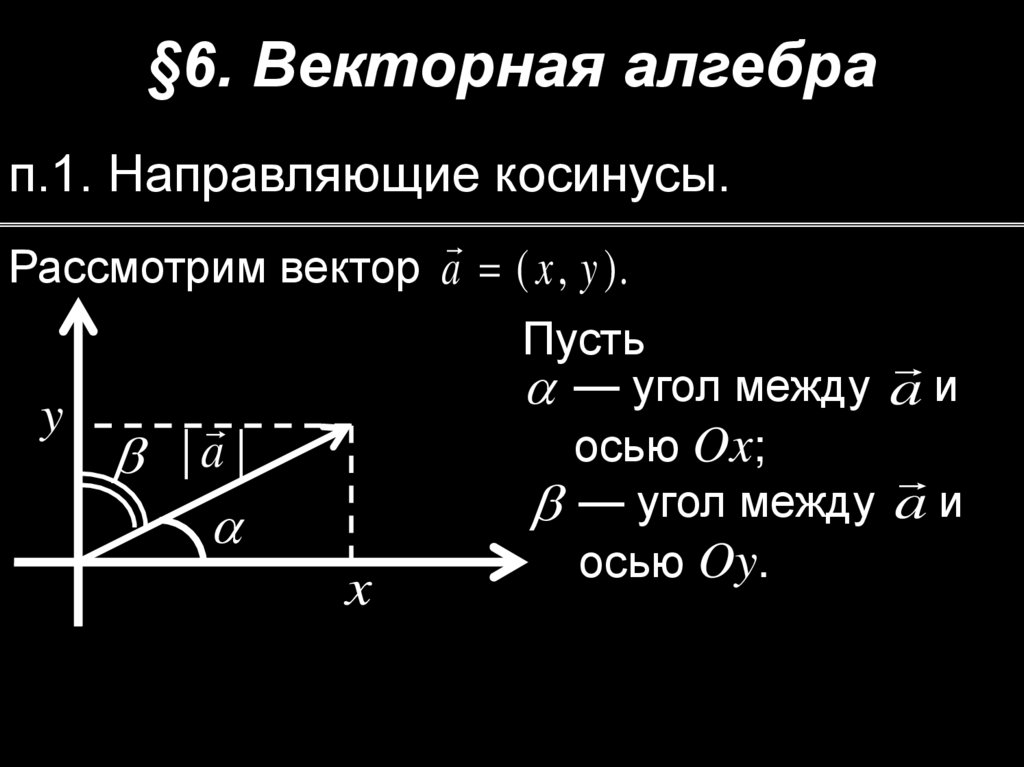
§6. Векторная алгебра
п.1. Направляющие косинусы.
Рассмотрим вектор a ( x , y ).
y
|a|
x
Пусть
— угол между a и
осью Ox;
— угол между a и
осью Oy.

2.

Очевидно
или
x | a | co s , y | a | co s
x
y
cos , cos .
|a|
|a|
Числа cos , cos называются направляющими
косинусами вектора a.
Так как
то
т.е.
2 2
2
|a | x y ,
2 2
2
2
2
| a | | a | cos | a | cos ,
cos cos 1 .
2
2

3.

Замечание.
Если
то
a ( x , y , z ),
x
y
z
cos , cos , cos .
|a|
|a|
|a|
При этом
cos cos cos 1 .
2
2
2

4.

Разложение вектора по ортам координатных
осей
Рассмотрим случай на плоскости.
Векторы
i (1, 0 ),
j ( 0 ,1)
называются ортами координатных осей.
Пусть a ( x , y ) —
произвольный вектор.
y N
j
O i
Рассмотрим векторы
a
M
x
OM ( x , 0 ), ON ( 0 , y ).

5.

Очевидно
Так как
то
OM x i , ON y j .
a OM ON ,
a xi yj
— формула разложения вектора по ортам
координатных осей.
Замечание.
Запись
a xi yj
равносильна записи
a ( x , y ).

6.

Замечание.
В пространстве ортами координатных осей
являются
векторы
i (1, 0 , 0 ),
j ( 0 ,1, 0 ), k ( 0 , 0 ,1).
Формула разложения вектора по ортам
координатных осей примет вид
a xi yj zk .
Пример. Найти направляющие косинусы
вектора
a i 2 j 2k .
Решение.
2
2
2
a (1, 2 , 2 ), | a | 1 ( 2 ) 2 3 ,
1
2
2
cos , cos , cos .
3
3
3

7.

п.2. Скалярное произведение.
Скалярным произведением
двух ненулевых
векторов a и b называется число, равное
произведению длин этих векторов на косинус
угла между ними
b
a
a b | a | | b | cos .
Угол между векторами
ab
cos .
| a || b |

8.

Свойства скалярного произведения
a b b a.
2)
( a ) b ( a b ), R .
Доказательство. Пусть 0 .
Тогда углы между векторами a , b и a , b равны,
( a ) b | a || b | cos | a || b | cos ( a b ).
Пусть 0 .
Тогда углы между векторами a , b и a , b
1)
являются смежными,
( a ) b | a || b | cos( ) | a || b | ( cos ) ( a b ).

9.

a (b c ) a b a c .
2 2
a | a | .
3)
4)
Доказательство.
2
2
a | a || a | cos 0 | a | .
Векторы называются ортогональными, если
угол между ними равен 900.
5) (критерий ортогональности).
Два вектора ортогональны тогда и только тогда,
когда их скалярное произведение
равно
нулю.
Доказательство. Пусть a b , т.е. 90 .
a b | a | | b | cos
90 0 .
ab
Если a b 0 , то cos 0, 90 .
| a || b |

10.

Выражение скалярного произведения через
координаты векторов
Замечание.
i i 1; i j 0; i k 0;
j j 1; j k 0 ; k k 1 .
Пусть
a ( x1 , y 1 , z 1 ) x1 i y 1 j z 1 k ,
b ( x2 , y2 , z2 ) x2i y2 j z2k .
Тогда

11.

a b ( x 1 i y 1 j z 1 k )( x 2 i y 2 j z 2 k )
x1 x 2 i i x1 y 2 i j x1 z 2 i k
y1 x 2 j i y1 y 2 j j y1 z 2 j k
z 1 x 2 k i z 1 y 2 k j z 1 z 2 k k x1 x 2 y 1 y 2 z 1 z 2 ,
a b x1 x 2 y 1 y 2 z 1 z 2 .
Пример. Найти угол между
векторами
a (1, 2 ,1), b ( 4 ,1, 1).
Решение. a b 1 4 ( 2 ) 1 1 ( 1) 1,
2
2
2
| a | 1 ( 2 ) 1 6 ,
ab
1
3
cos
.
| a || b |
6 3 2 18
| b | 4 2 1 2 ( 1) 2 3 2 ,

12.

п.3. Векторное произведение.
Три вектора в пространстве называются
компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.

13.

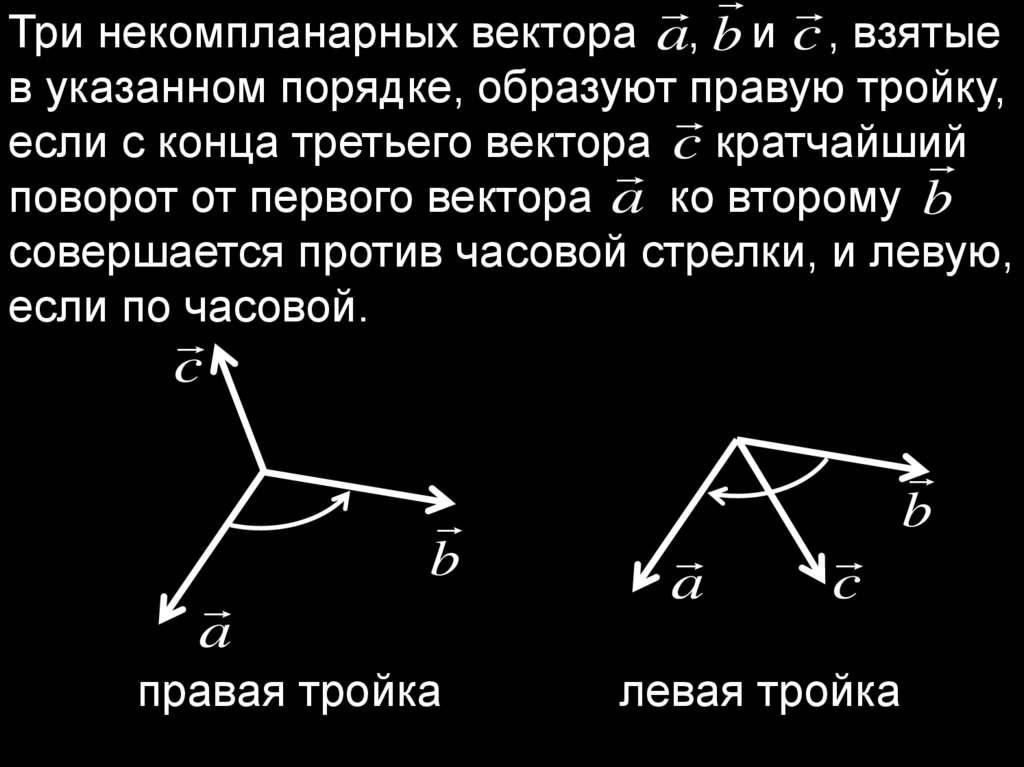
Три некомпланарных вектора a, b и c , взятые
в указанном порядке, образуют правую тройку,
если с конца третьего вектора c кратчайший
поворот от первого вектора a ко второму b
совершается против часовой стрелки, и левую,
если по часовой.
c
a
b
правая тройка
a
c
левая тройка
b

14.

Векторным
на
a
произведением вектора
вектор b называется вектор c,
удовлетворяющий условиям:
1) c a , c b ;
2) | c | | a | | b | sin( a , b );
3) a , b , c — правая тройка.
Обозначается:
a b , [ a , b ].

15.

Свойства векторного произведения
1)
Доказательство.
a b ( b a ).
a b || ( b a );
| a b | | ( b a ) | .
Так как
a , b , a b — правая тройка,
a , b , b a — левая тройка,
то
a b , ( b a ) противоположно направлены.
Значит,
a b ( b a ).

16.

2)
3)
( a b ) ( a ) b a ( b ), R .
a || b
a b 0.
Доказательство самостоятельно.
4)
(a b ) c a c b c .

17.

Выражение векторного произведения через
координаты векторов
k
Замечание.
i
i i 0;
i j k;
i k j;
j
j i k ;
j j 0;
j k i;
k i j;
k j i ;
k k 0.

18.

Пусть
Тогда
a ( x1 , y 1 , z 1 ) x1 i y 1 j z 1 k ,
b ( x2 , y2 , z2 ) x2i y2 j z2k .
a b ( x1 i y 1 j z 1 k ) ( x 2 i y 2 j z 2 k )
x1 x 2 ( i i ) x1 y 2 ( i j ) x1 z 2 ( i k )
y1 x 2 ( j i ) y1 y 2 ( j j ) y1 z 2 ( j k )
z1 x 2 ( k i ) z1 y 2 ( k j ) z1 z 2 ( k k )

19.

0 x1 y 2 k x1 z 2 j y 1 x 2 k 0 y 1 z 2 i z 1 x 2 j z 1 y 2 i 0
( y 1 z 2 z 1 y 2 ) i ( x1 z 2 j z 1 x 2 ) j ( x1 y 2 k y 1 x 2 ) k
y1
y2
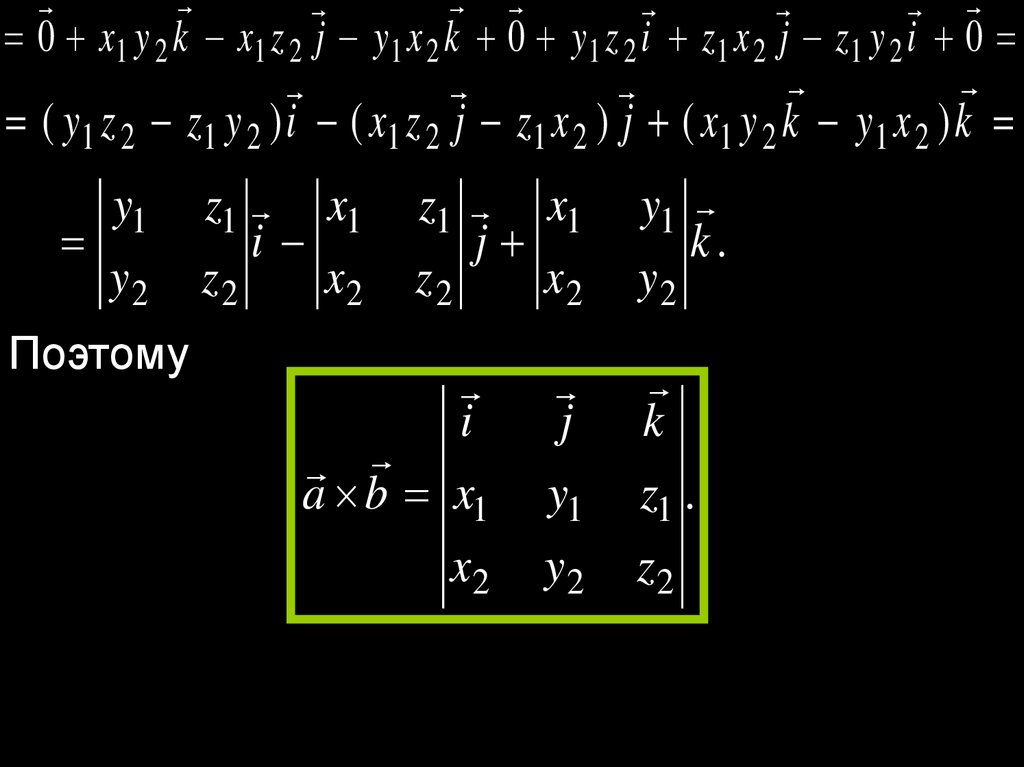
Поэтому
z1 x1
i
z2
x2
z1 x1
j
z2
x2
i
a b x1
x2
j
y1
y2
y1
k.
y2
k
z1 .
z2

20.

Геометрический смысл векторного
произведения
a
b
S | a | | b | sin
S | a b |
a
b
1
S | a | | b | sin
2
1
S | a b |
2

21.

п.4. Смешанное произведение.
Смешанным произведением векторов a ,b и c,
взятых в указанном порядке называется
скалярное произведение векторного
произведения первых двух векторов a и b на
третий вектор c .
Обозначается:
Таким образом
ab c.
a b c (a b ) c .

22.

Свойства смешанного произведения
1)
( a b ) c (b c ) a (c a ) b .
2)
( a b ) c a ( b c ).
3)
4)
ab c acb ;
a b c b a c ;
ab c c b a.
a , b , c ко м пла на р н ы
ab c 0.

23.

Выражение смешанного произведения через
координаты векторов
Пусть
Тогда
a ( x1 , y 1 , z 1 ) x1 i y 1 j z 1 k ,
b ( x2 , y2 , z2 ) x2i y2 j z2k .
c ( x3 , y3 , z3 ) x3i y3 j z3 k .

24.

a b c (a b ) c
y1
y2
z1 x1
i
z2
x2
z1 x1
j
z2
x2
y1 z1
x1
x3
y2 z2
x2
Поэтому
y1
k ( x3 i y 3 j z 3 k )
y2
z1
x1
y3
z2
x2
x1
a b c x2
x3
y1
y2
y3
y1
z3 .
y2
z1
z2 .
z3

25.

Приложения смешанного произведения
1) Если
то
a,b , c
если
то
a b c 0,
— правая тройка;
a b c 0,
a , b , c — левая тройка.

26.

2)
d
Пусть
тогда
c
b
a
d a b,
a b c ( a b ) c d c | d | п р d c .

27.

Но
| d | | a b | S ,
прd c H .
Значит,
a b c S H V
V | a b c | .
или
Объем треугольной пирамиды
1
1
V SH | a b c | .
3
6