Similar presentations:
Спектры периодических и непериодических сигналов. Лекция 3
1. Дисциплина «Цифровая обработка сигналов»
Тема: Спектры периодических инепериодических сигналов
Лекция 3
1
2. Цель лекции: Изучить спектры периодических и непериодических сигналов
План:1. Ряды Фурье
2. Спектры периодических сигналов
3. Преобразование Фурье
4. Спектры непериодических сигналов
3. Ряд Фурье. Спектры периодических сигналов
Периодические негармонические функции можноразложить в ряд Фурье. Для этого периодическая
функция должна удовлетворять условиям Дирихле:
1. Иметь конечное число разрывов первого рода
(скачков) на периоде Т,
2. Иметь конечное число экстремумов (максимумов и
минимумов).
Ряд Фурье имеет несколько форм записи:
1. Синусно-косинусная,
2. Вещественная,
3. Комплексная.
4. Периодические негармонические функции:
5. Синусно-косинусная форма ряда Фурье:
a0f (t ) аk cos k 1t bk sin k 1t.
2 k 1
k 1
6.
Ta0 1
f (t ) dt
2 Т 0
- постоянный коэффициент ряда Фурье
Т
2
ak f (t ) cos( k 1 t )dt
T 0
T
2
bk f t sin( k 1 t ) dt
T 0
-коэффициенты косинусной
составляющей ряда Фурье
-коэффициенты синусной
составляющей ряда Фурье
7.
номер гармоники,k
–
k 1
– основная гармоника;
a0
2
– постоянная составляющая,
нулевая гармоника ряда Фурье;
ak , bk
2
1
Т
T
– коэфициенты ряда Фурье(амплитуды гармоник);
– частота основной гармоники
– период периодической функции.
k 1,2,3..., – номер гармоники
8. Вещественная форма ряда Фурье
a0f (t ) ck sin k 1t k
2 k 1
9.
сk a b2
k
2
k
ak
k arctg
bk
10.
Комплексная форма ряда ФурьеКомплексная форма:
f (t ) Ak e
jk 1 t
k
Комплексные коэффициенты ряда Фурье:
T
1
jk 1t
Ak f (t )e
dt Ak ( jk 1 )
T 0
Ak A(k 1 )e
j ( k 1 )
- комплексным частотным спектром
11.
Составляющие:A(k 1 )
- амплитудным спектром
(k 1 ) - фазовым спектром
Периодические функции имеют дискретный или
линейчатый спектр
12.
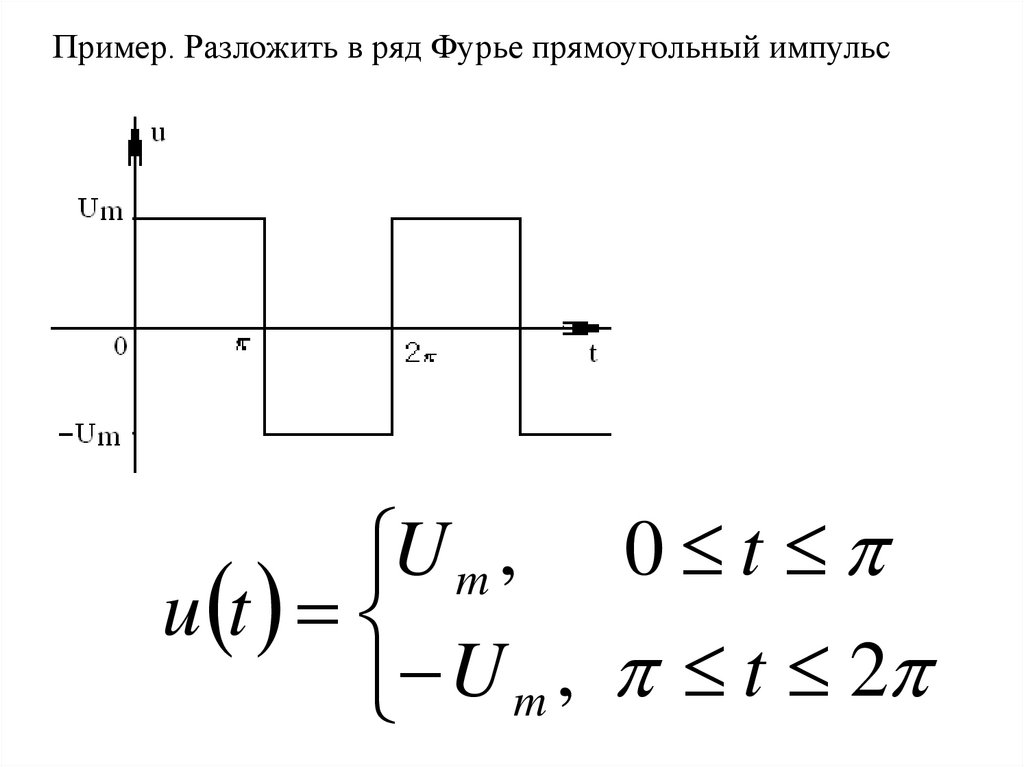
Пример. Разложить в ряд Фурье прямоугольный импульсU m , 0 t
u t
U m , t 2
13.
a0f t ak cos k 1t bk sin k 1t
2 k 1
k 1
T
2
2
а0 1
1
1
f (t )dt
f (t )dt
U m dt U m dt 0.
2 T 0
2 0
2 0
0
14.
T2
2
2
ak f (t ) cos ktdt
U m cos ktdt U m cos ktdt
T 0
2 0
2
Um
cos ktdt cos ktdt
0
Um 1
1
2
sin kt 0 sin kt 0;
k
k
ak 0 при любом k .
15.
22
2
bk f (t ) sin ktdt
U m sin k tdt U m sin k tdt
T 0
2 0
T
Um 1
1
2
cos kt 0 cos kt
k
k
Um
cos k cos 0 cos 2k cos k
k
k четное, bk 0
4U m
k нечетное, bk k k 1,3,5,7
16.
4 U mf (t ) bk sin 1t
sin 1t
k 1, 3, 5....
k 1, 3, 5.... k
4U m
4U m
4U m
f (t )
sin 1t
sin 3 1t
sin 5 1t...
3
5
u 63,66 sin 1t 21,22 sin 3 1t 12,73 sin 5 1t ...
17.
ПРИМЕР №1. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ ДВУПОЛЯРНОГО ИМПУЛЬСА ПРЯМОУГОЛЬНОЙ ФОРМЫu ( t)
Um if 0 t
( Um) if t 2
100
u( t)
0
100
0
2
4
6
8
t
2
1
a0
T 0
u ( t) dt 0
2
ak ( k)
T 0
2
u ( t) cos ( k t) dt
2
b ( k)
T 0
2
u ( t) sin ( k t) dt
18.
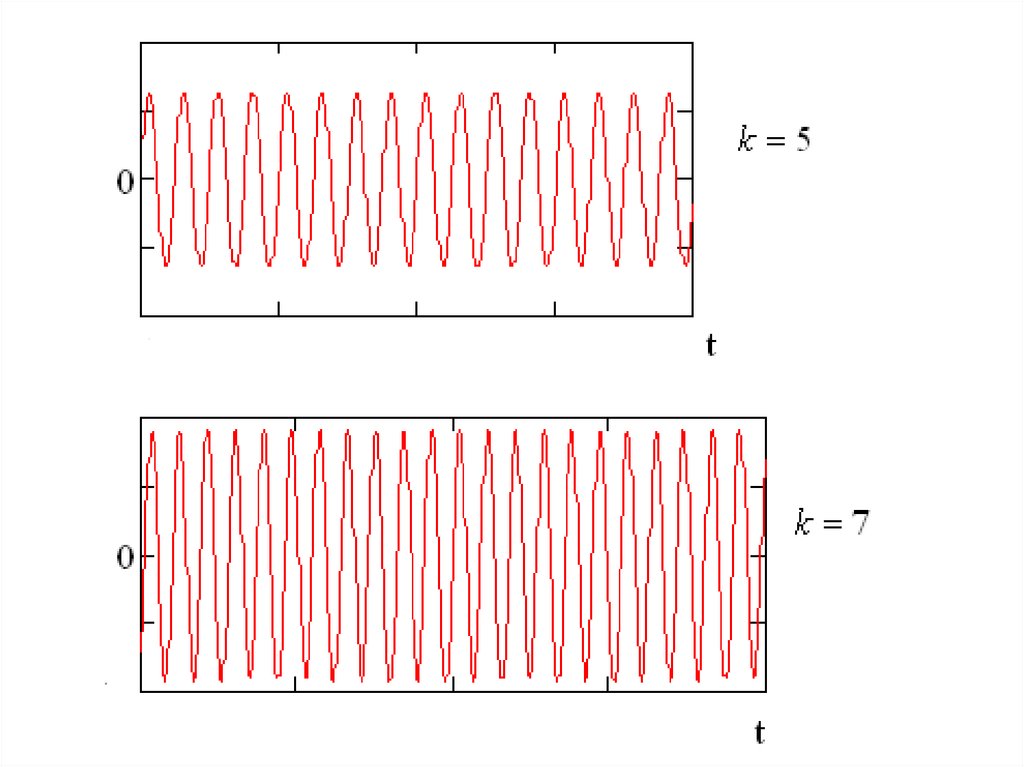
u1 ( t) 63.662 sin ( t)u3 ( t) 21.221 sin ( 3 t)
u5 ( t) 12.732 sin ( 5 t)
u7 ( t) 9.095 sin ( 7 t)
u9 ( t) 7.074 sin ( 9 t)
u11 ( t) 5.787 sin ( 11 t)
k 1 3 11
19.
20.
21.
22.
23.
Периодические функции имеют линейчатый спектр, т.е.спектр периодических функций дискретный.
24.
Спектр непериодических сигналов можно получить спомощью преобразования Фурье.
Преобразование Фурье позволяет получить спектральные
функции непериодических функций.
Непериодическую функцию времени, удовлетворяющую
условиям Дирихле и абсолютно интегрируемая в
бесконечных пределах может быть преобразована в
частотную область с помощью преобразования Фурье.
25. Преобразование Фурье
F ( j ) f (t ) ej t
dt
прямое двухстороннее
преобразование Фурье
Если выполняется условие:
0, t 0
f (t )
f (t ), t 0
преобразование Фурье называется односторонним
преобразование Фурье
26.
F ( j ) f (t ) ej t
dt
0
f (t )
непериодическая функция времени
F ( j ) спектральная плотность, спектральная функция,
спектр непериодической функции
1
j t
f (t )
F ( j ) e d
2
обратное преобразование Фурье
27.
f (t ) абсолютно интегрируемые функции вбесконечном интервале
Преобразование Фурье – частный случай преобразования
Лапласа при p j
F ( j ) F ( p ) p j
F ( p) f (t )e p t dt ,
p j
28.
F ( j ) f (t ) ej t
dt
0
f (t )
непериодическая функция времени
F ( j ) спектральная плотность, спектральная функция,
спектр непериодической функции
1
j t
f (t )
F ( j ) e d
2
обратное преобразование Фурье
29.
Эти формулы позволяют преобразоватьнепериодическую функцию времени f (t )
в
функцию частоты F ( j ).
Так
как
спектральная F ( j )функция
комплексная величина, ее можно показать в
показательной и в алгебраической форме.
30.
F ( j ) F ( j ) ej ( )
A( ) jB( )
F ( j ) Модуль называется амплитудный спектр,
четная функция
( )
Аргумент называется фазовый спектр,
нечетная функция.
31.
1. Определить спектр функцииf (t ) e
t
Изображение по Лапласу функции f (t ) e
e
t
1
p
1
F ( p)
p p j
.
t
:
32.
Спектральная функция:1
1
F ( j )
e
j
2 2
j arctg
Амплитудный спектр:
S ( ) F ( j )
1
2
Фазовый спектр:
( ) arctg .
2
.
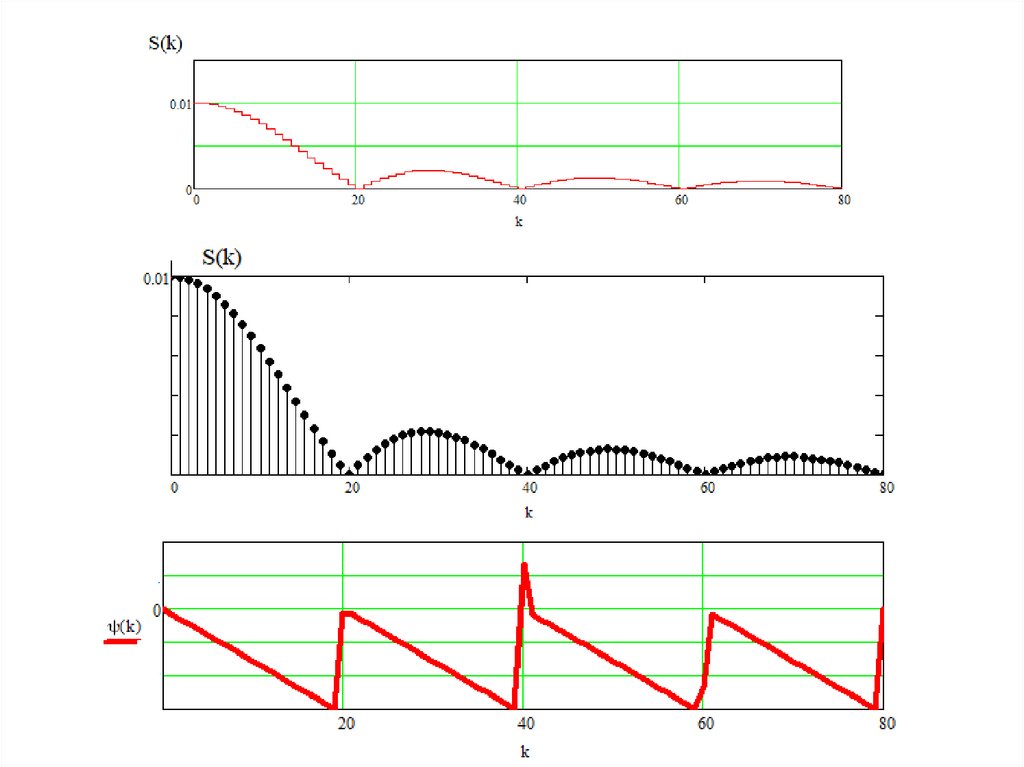
33. Графики
S ( ), ( )Спектр непериодической функции сплошной
34.
Пример. Спектр прямоугольного импульса15
15
10
u( t )
5
0
0
0
0
5 10
3
0.01
t
0.015
0.02
0.02
35.
36.
37.
Спектр непериодической функции сплошной.38. Контрольные вопросы
1. Из каких тригонометрических функций формируетсяпериодический сигнал?
2. Что такое постоянная составляющая ряда Фурье?
3. Какие формы ряда Фурье используются для описания
периодических сигналов?
4. Что такое амплитудный спектр и фазовый спектр?
5. Какой вид имеет амплитудный и фазовый спектр
периодических сигналов?
6. Какой вид имеет амплитудный и фазовый спектр
непериодических сигналов?
7. Какие функции могут быть разложены в
тригонометрический ряд Фурье?
38








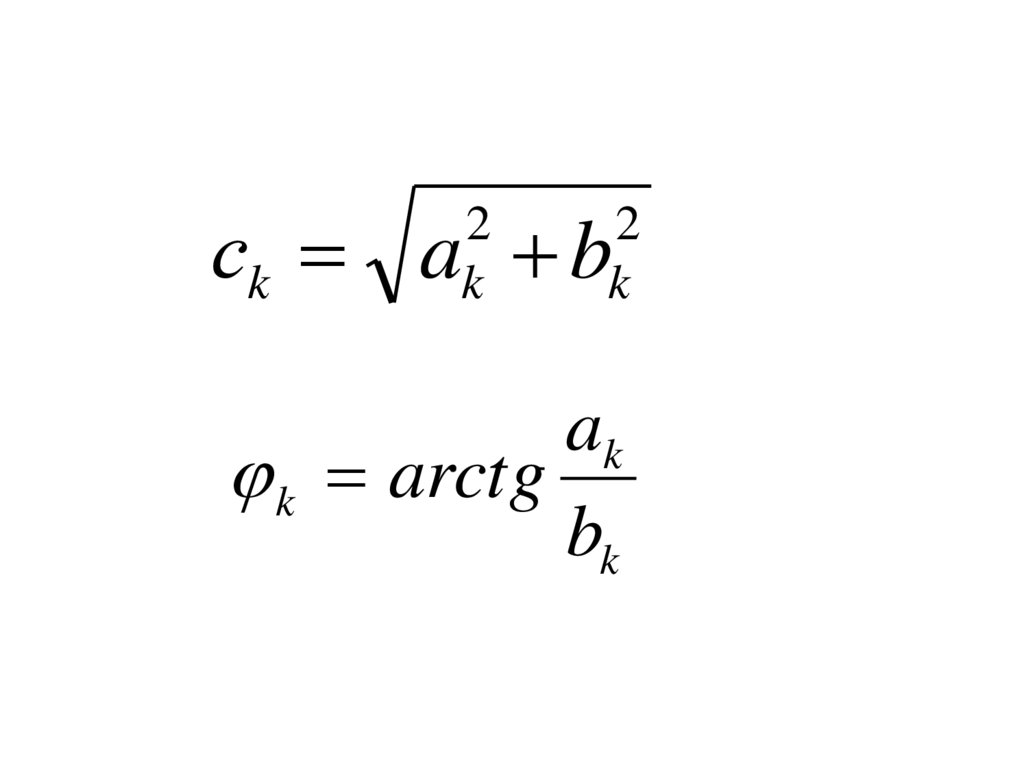


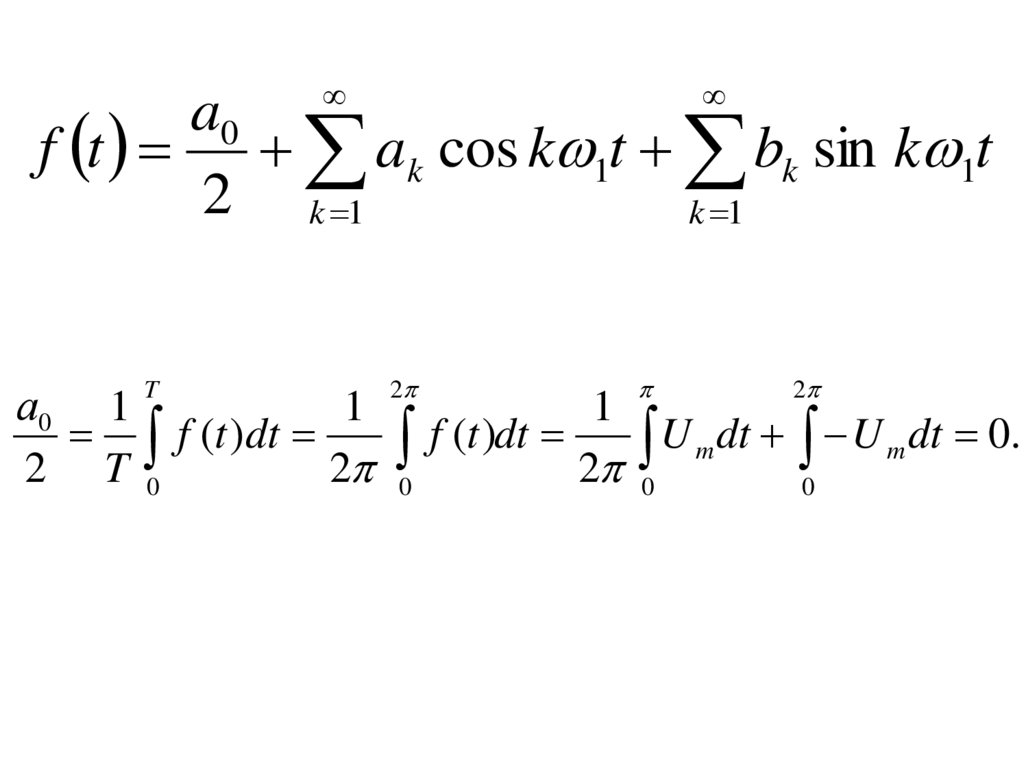
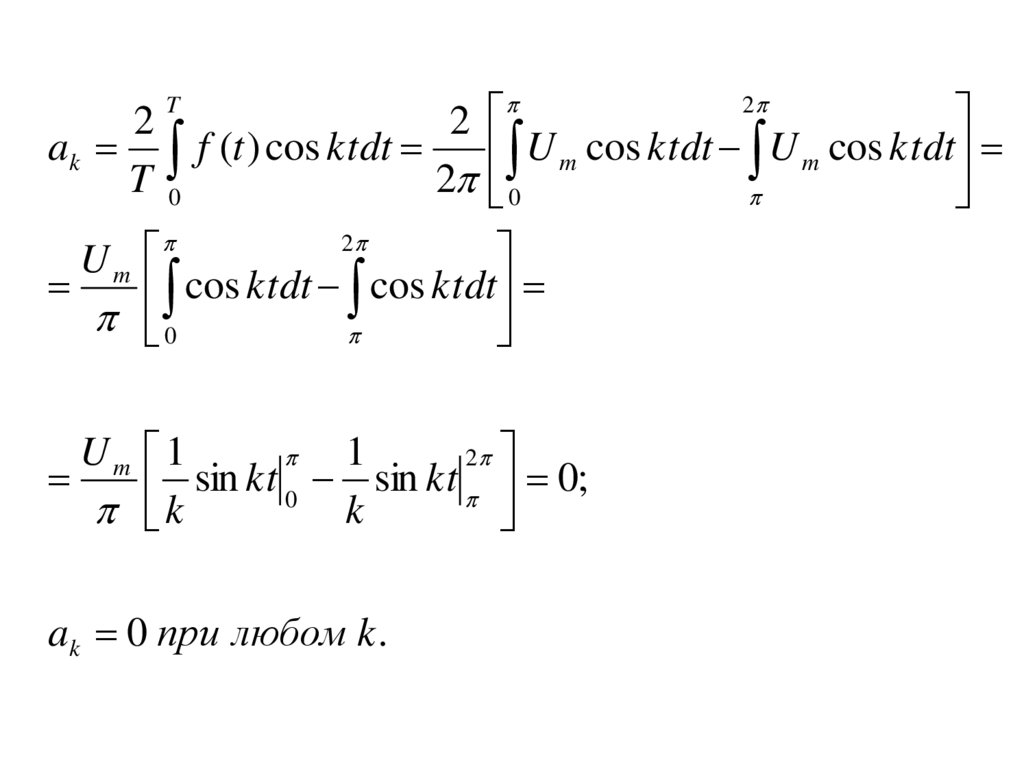
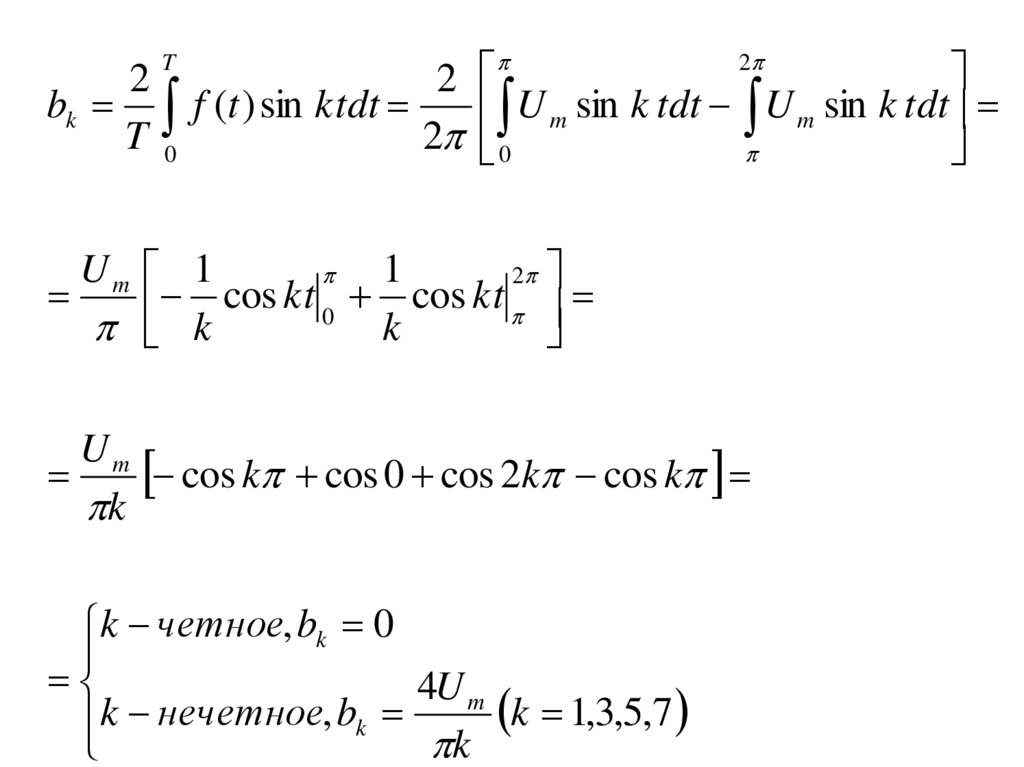





















 electronics
electronics








