Матрицы. Виды матриц. Операции над матрицами (тема 1)

1. Тема 1. Матрицы. Виды матриц. Операции над матрицами.

К.э.н., ассоц.проф.Мадиярова К.З.

2.

ПЛАН ЛЕКЦИИ
1. ПОНЯТИЕ И ВИДЫ МАТРИЦ
2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ
И РАЗМЕР МАТРИЦ
3. ОПЕРАЦИИ НАД МАТРИЦАМИ

3.

ОПРЕДЕЛЕНИЯ
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА,
ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ,
НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.

4.

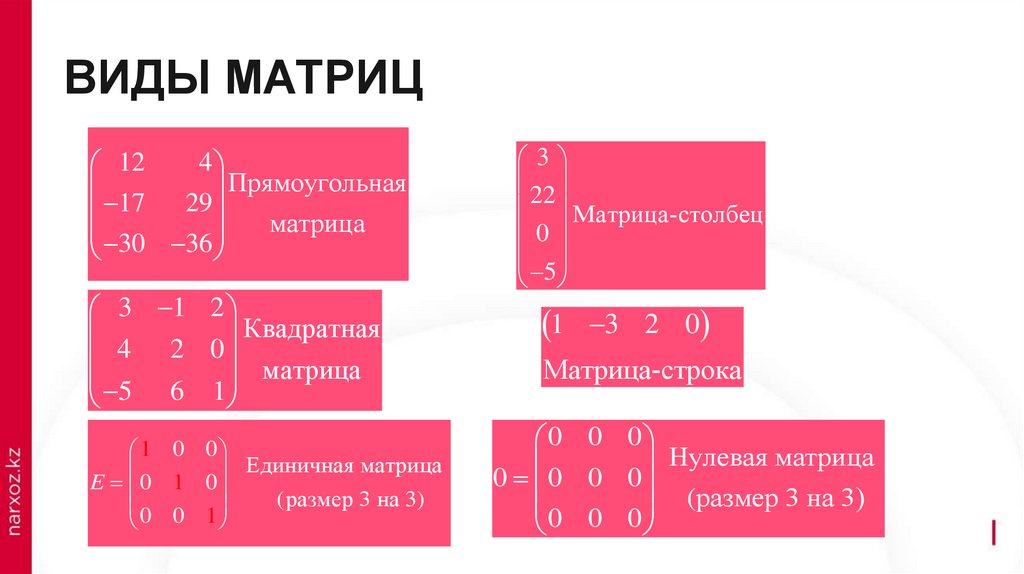
ВИДЫ МАТРИЦ
4
12
17 29 Прямоугольная
матрица
30 36
3 1 2
4 2 0 Квадратная
матрица
5 6 1
1 0 0
Единичная матрица
E 0 1 0
(размер 3 на 3)
0 0 1
3
22
Матрица-столбец
0
5
1 3 2
0
Матрица-строка
0 0 0
Нулевая матрица
0 0 0 0
(размер 3 на 3)
0 0 0

5.

РАЗМЕР МАТРИЦЫ
МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n
СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ
РАЗМЕРА m НА n.
4
12
17 29 Матрица размера 3 на 2
(3 строки, 2 столбца)
30 36

6.

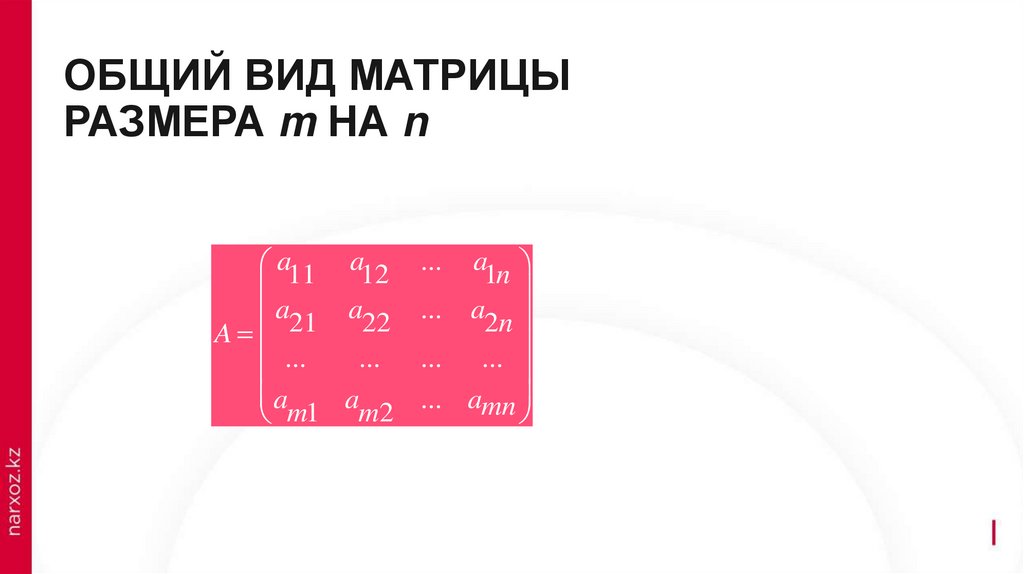
ОБЩИЙ ВИД МАТРИЦЫ
РАЗМЕРА m НА n
a11 a12
a21 a22
A
...
...
a
m1 am2
a1n
... a2n
... ...
... amn
...

7.

ЭЛЕМЕНТ МАТРИЦЫ
4 Элемент a31 a-три-один 30
12
17 29
(3-я строка,1-й столбец)
30 36

8.

ОПЕРАЦИИ НАД
МАТРИЦАМИ
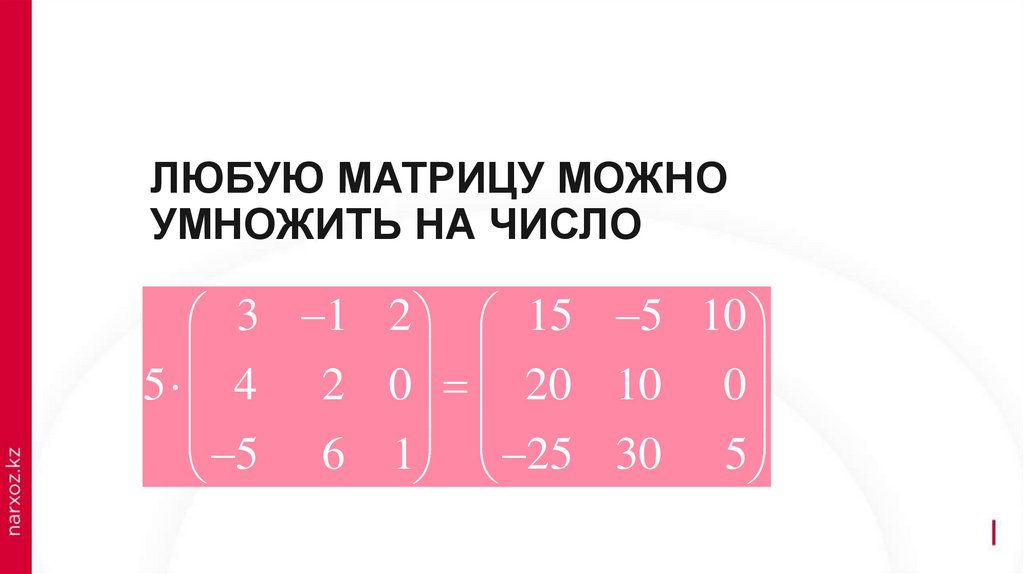
ЛЮБУЮ МАТРИЦУ МОЖНО
УМНОЖИТЬ НА ЧИСЛО
3 1 2 15 5 10
5 4 2 0 20 10 0
5 6 1 25 30 5

9.

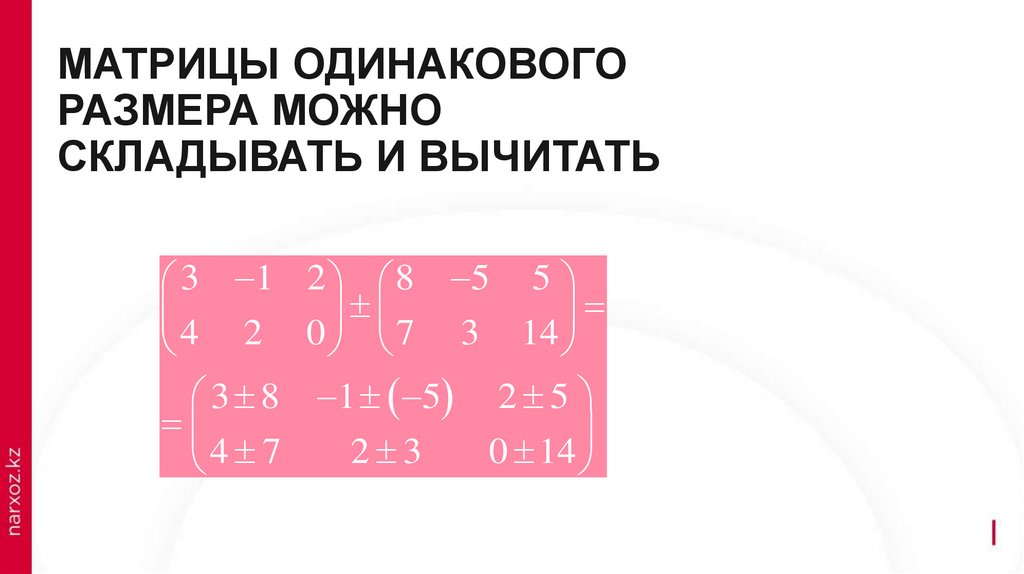
МАТРИЦЫ ОДИНАКОВОГО
РАЗМЕРА МОЖНО
СКЛАДЫВАТЬ И ВЫЧИТАТЬ
3 1 2 8 5 5
4 2 0 7 3 14
3 8 1 5 2 5
2 3
0 14
4 7

10.

ТРАНСПОНИРОВАНИЕ
МАТРИЦЫ
4
12
Исходная
A 17
29
матрица (размер 3 на 2)
30 36
12 17 30 Транспонированная
A
матрица (размер 2 на 3)
4
29
36
T

11.

ВОЗМОЖНОСТЬ УМНОЖЕНИЯ
МАТРИЦЫ НА МАТРИЦУ
МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА,
МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА
И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО
СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ
СТРОК МАТРИЦЫ B
(m x n)•(n x m) = (m x m)

12.

УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ
(СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
7
2 5 3 0 2 7 5 0 3 4 2
4

13.

ПРАВИЛО УМНОЖЕНИЯ
МАТРИЦЫ НА МАТРИЦУ
КАЖДАЯ СТРОКА ЛЕВОЙ
МАТРИЦЫ СКАЛЯРНО
УМНОЖАЕТСЯ НА КАЖДЫЙ
СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
С A B
A левая матрица, B правая матрица

14.

ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
3 1 2 8 1
4 2 0 7 2
5 6 1 2 3
3 8 1 7 2 2 3 1 1 2 2 3 21 5
4 8 2 7 0 2
4 1 2 2 0 3 46 8
5 8 6 7 1 2 5 1 6 2 1 3 4 4

15.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Определитель (детерминант) матрицы — некоторое число,
с которым можно сопоставить любую квадратную матрицу

16.

ОБРАТНАЯ МАТРИЦА
Обра́тная ма́трица — такая матрица A−1, при умножении на
которую исходная матрица A даёт в результате единичную
матрицу E:

17.

Правила ввода табличных
формул в EXCEL
Перед вводом табличной формулы следует выделить
ячейку (интервал ячеек), в которой будет содержаться
результат. Если результат вычисления по формуле
множественный, то выделенный интервал должен
иметь в точности требуемый размер и форму.
Далее следует напечатать формулу и для завершения
ее ввода нажать клавиши Crtl +Shift+Enter . Введенная
формула в строке формул заключается в фигурные
скобки, что свидетельствует о том, что это - табличная
формула, Никогда не вводите фигурные скобки сами,
так как в этом случае формула будет восприниматься
как текст.

18.

Встроенные функции для
операций с матрицами
Для выполнения некоторых операций с
матрицами в Excel есть ряд встроенных
функций:
• МОПРЕД Возвращает определитель матрицы
(матрица хранится в массиве).
• МОБР Возвращает обратную матрицу для
матрицы, хранящейся в массиве.
• МУМНОЖ Возвращает произведение матриц
• ТРАНСП Возвращает транспонированный
массив

19.

Спасибо за внимание!