Similar presentations:
Обыкновенные дроби
1. ОБЫКНОВЕННЫЕ ДРОБИ
2.
2 35 5
из двух дробей с одинаковыми
знаменателями меньше та, у которой
меньше числитель, и больше та, у
которой больше числитель
3.
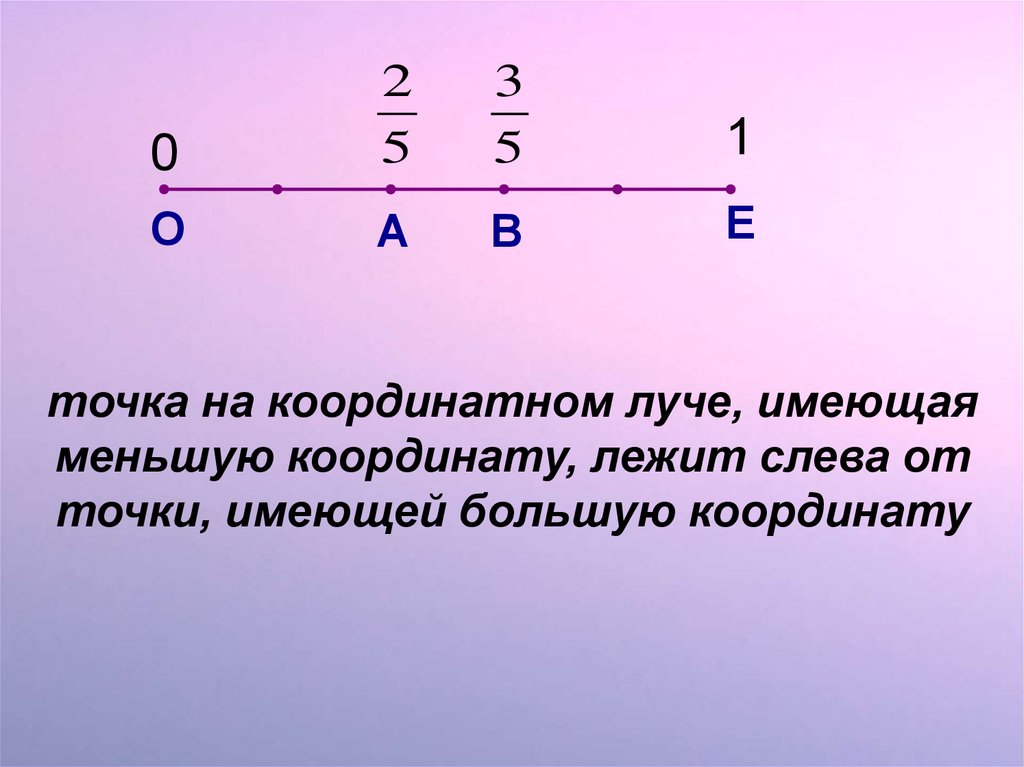
02
5
3
5
1
О
А
В
Е
точка на координатном луче, имеющая
меньшую координату, лежит слева от
точки, имеющей большую координату
4.
38
- ПРАВИЛЬНАЯ ДРОБЬ
ПРАВИЛЬНАЯ ДРОБЬ – ЭТО ДРОБЬ, В КОТОРОЙ
ЧИСЛИТЕЛЬ МЕНЬШЕ ЗНАМЕНАТЕЛЯ
8 11
,
8 8
- НЕПРАВИЛЬНЫЕ ДРОБИ
НЕПРАВИЛЬНАЯ ДРОБЬ – ЭТО ДРОБЬ, В
КОТОРОЙ ЧИСЛИТЕЛЬ БОЛЬШЕ ЗНАМЕНАТЕЛЯ
ИЛИ РАВЕН ЕМУ
5.
03
8
О
А
8
1=
8
Е
11
8
В
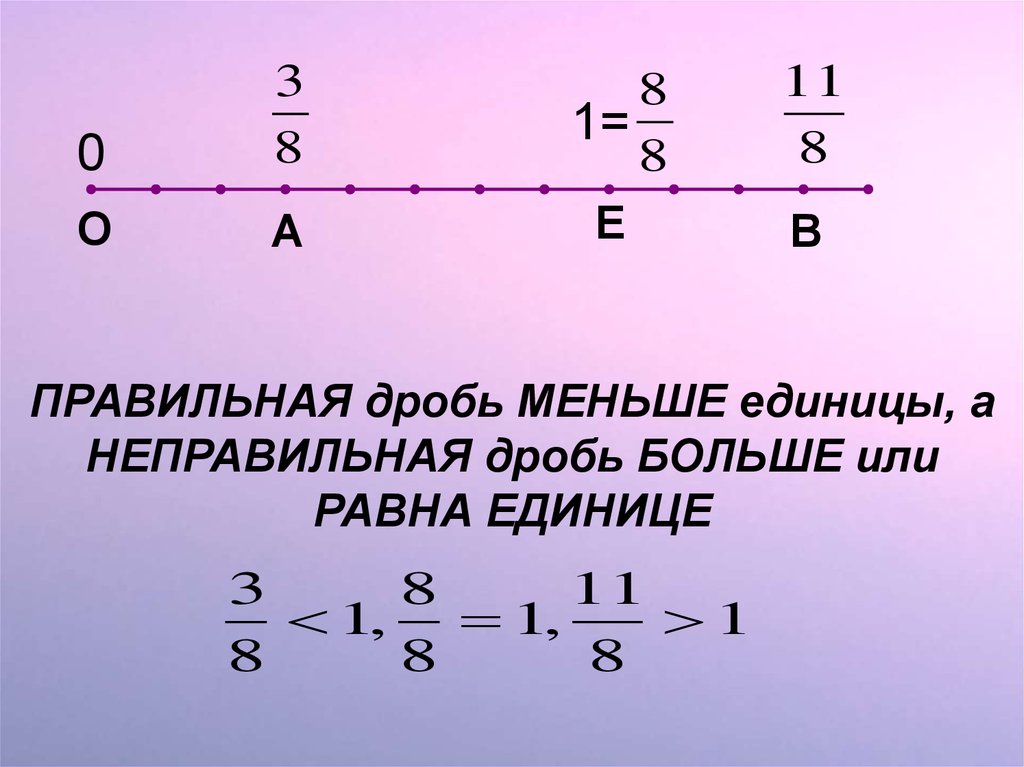
ПРАВИЛЬНАЯ дробь МЕНЬШЕ единицы, а
НЕПРАВИЛЬНАЯ дробь БОЛЬШЕ или
РАВНА ЕДИНИЦЕ
3
8
11
1,
1,
1
8
8
8
6.
2 52 5
7
8 8
8
8
при СЛОЖЕНИИ ДРОБЕЙ С
ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
числители складывают, а
знаменатель оставляет тот же
a
b
a b
c
c
c
7.
7 47 4
3
8 8
8
8
при ВЫЧИТАНИИ ДРОБЕЙ С
ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ из
числителя уменьшаемого вычитают
числитель вычитаемого, а знаменатель
оставляет тот же
a b
a b
c
c
c
8.
ЧЕРТУ ДРОБИ можно приниматьКАК ЗНАК ДЕЛЕНИЯ:
2
2:3
3
9.
с помощью дробей можно записать результатделения двух любых натуральных чисел
если деление выполняется НАЦЕЛО, то ЧАСТНОЕ
является НАТУРАЛЬНЫМ ЧИСЛОМ
если разделить НАЦЕЛО НЕЛЬЗЯ, то ЧАСТНОЕ
является ДРОБНЫМ ЧИСЛОМ
27
27 : 3
9
3
5
5:6
6
3
3 :1 3
1
9
9:4
4
10.
22
сумму 1 принято записывать короче: 1
3
3
одна целая две третьих
целая часть
2
1
3
дробная часть
5
2
1
3
3
5
чтобы перейти от записи
3
2
к записи 1
, надо разделить 5 на 3.
3
получим неполное частное 1 и остаток 2.
число 1 дает целую часть, а остаток 2 –
числитель дробной части
11. ЧТОБЫ ИЗ НЕПРАВИЛЬНОЙ ДРОБИ ВЫДЕЛИТЬ ЦЕЛУЮ ЧАСТЬ, надо:
1.2.
3.
разделить с остатком числитель на
знаменатель;
неполное частное будет целой частью;
остаток (если он есть) дает числитель, а
делитель – знаменатель дробной части.
знаменатель
47
9
47 9
45 .5
числитель
2
47
2
5
9
9
целая
часть
12. ЧТОБЫ ПРЕДСТАВИТЬ СМЕШАННОЕ ЧИСЛО В ВИДЕ НЕПРАВИЛЬНОЙ ДРОБИ нужно:
1.2.
3.
умножить его целую часть на знаменатель
дробной части;
к полученному произведению прибавить
числитель дробной части;
записать полученную сумму числителем
дроби, а знаменатель дробной части
оставить без изменения.
13.
ПРИ СЛОЖЕНИИ (И ВЫЧИТАНИИ) чисел всмешанной записи целые части складывают
(вычитают) отдельно, а дробные - отдельно
если в дробной части неправильная дробь, то
из нее выделяют целую часть и добавляют ее
к уже имеющейся целой части
7
4
11
11
2
2
3 2 5 5
5 1 6
9
9
9
9
9
9
14.
если при вычитании смешанных чисел дробнаячасть уменьшаемого меньше дробной части
вычитаемого, поступают так:
3
5
3
5
3
5
6 2 6 2 5 1 2
7
7
7
7
7
7
3
5
10
5
10
5
5
5 1 2 5
2 3
2 5
7
7
7
7
7
7
7
3
5
10
5
5
6 2 5
2 3
7
7
7
7
7
15.
таким же образом поступают привычитании дроби из натурального
числа, и при вычитании смешанного
числа из натурального числа
5
8 5
3
4 3 3
8
8 8
8
5
6
5
1
8 3 7 3 4
6
6
6
6
16.
15 3=
20 4
ДЕЛЕНИЕ ЧИСЛИТЕЛЯ И
ЗНАМЕНАТЕЛЯ НА ИХ ОБЩИЙ
ДЕЛИТЕЛЬ, ОТЛИЧНЫЙ ОТ
ЕДИНИЦЫ, НАЗЫВАЮТ
СОКРАЩЕНИЕМ ДРОБИ.
17.
3 6=
4 8
ЧИСЛО, НА КОТОРОЕ НАДО УМНОЖИТЬ
ЗНАМЕНАТЕЛЬ ДРОБИ, ЧТОБЫ ПОЛУЧИТЬ
НОВЫЙ ЗНАМЕНАТЕЛЬ НАЗЫВАЮТ
ДОПОЛНИТЕЛЬНЫМ МНОЖИТЕЛЕМ.
ПРИ ПРИВЕДЕНИИ ДРОБИ К НОВОМУ
ЗНАМЕНАТЕЛЮ ЕЁ ЧИСЛИТЕЛЬ И
ЗНАМЕНАТЕЛЬ УМНОЖАЮТ НА
ДОПОЛНИТЕЛЬНЫЙ МНОЖИТЕЛЬ
18.
ЧТОБЫ СРАВНИТЬ (СЛОЖИТЬ, ВЫЧЕСТЬ)ДРОБИ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ,
НАДО:
1. ПРИВЕСТИ ДАННЫЕ ДРОБИ К
ОБЩЕМУ ЗНАМЕНАТЕЛЮ;
1. СРАВНИТЬ (СЛОЖИТЬ, ВЫЧЕСТЬ)
ПОЛУЧЕННЫЕ ДРОБИ.
19.
ЧТОБЫ УМНОЖИТЬ ДРОБЬ НА НАТУРАЛЬНОЕЧИСЛО, НАДО ЕЁ ЧИСЛИТЕЛЬ УМНОЖИТЬ НА
ЭТО ЧИСЛО, А ЗНАМЕНАТЕЛЬ ОСТАВИТЬ БЕЗ
ИЗМЕНЕНИЯ.
c
20.
ЧТОБЫ УМНОЖИТЬ ДРОБЬ НА ДРОБЬ,НАДО:
1. НАЙТИ ПРОИЗВЕДЕНИЕ
ЧИСЛИТЕЛЕЙ И ПРОИЗВЕДЕНИЕ
ЗНАМЕНАТЕЛЕЙ ЭТИХ ДРОБЕЙ;
2. ПЕРВОЕ ПРОИЗВЕДЕНИЕ ЗАПИСАТЬ
ЧИСЛИТЕЛЕМ, А ВТОРОЕ –
ЗНАМЕНАТЕЛЕМ.
x
=
21.
ДЛЯ ТОГО, ЧТОБЫ ВЫПОЛНИТЬУМНОЖЕНИЕ СМЕШАННЫХ
ЧИСЕЛ,
НАДО ИХ ЗАПИСАТЬ В ВИДЕ
НЕПРАВИЛЬНЫХ ДРОБЕЙ, А
ЗАТЕМ ВОСПОЛЬЗОВАТЬСЯ
ПРАВИЛОМ УМНОЖЕНИЯ ДРОБЕЙ.
22.
ЧТОБЫ УМНОЖИТЬ СМЕШАННОЕЧИСЛО НА НАТУРАЛЬНОЕ ЧИСЛО,
МОЖНО:
1. УМНОЖИТЬ ЦЕЛУЮ ЧАСТЬ НА
НАТУРАЛЬНОЕ ЧИСЛО;
2. УМНОЖИТЬ ДРОБНУЮ ЧАСТЬ НА
НАТУРАЛЬНОЕ ЧИСЛО;
3. СЛОЖИТЬ ПОЛУЧЕННЫЕ
РЕЗУЛЬТАТЫ.
23.
ЧТОБЫ разделитьДРОБЬ на
натуральное число,
НАДО:
1. Если числитель делится нацело на
это число , то разделить и
записать в числитель, а
знаменатель переписать;
2. Если числитель не делится нацело
на это число , то числитель
переписать, а знаменатель
умножить на это число и записать
в знаменатель.
















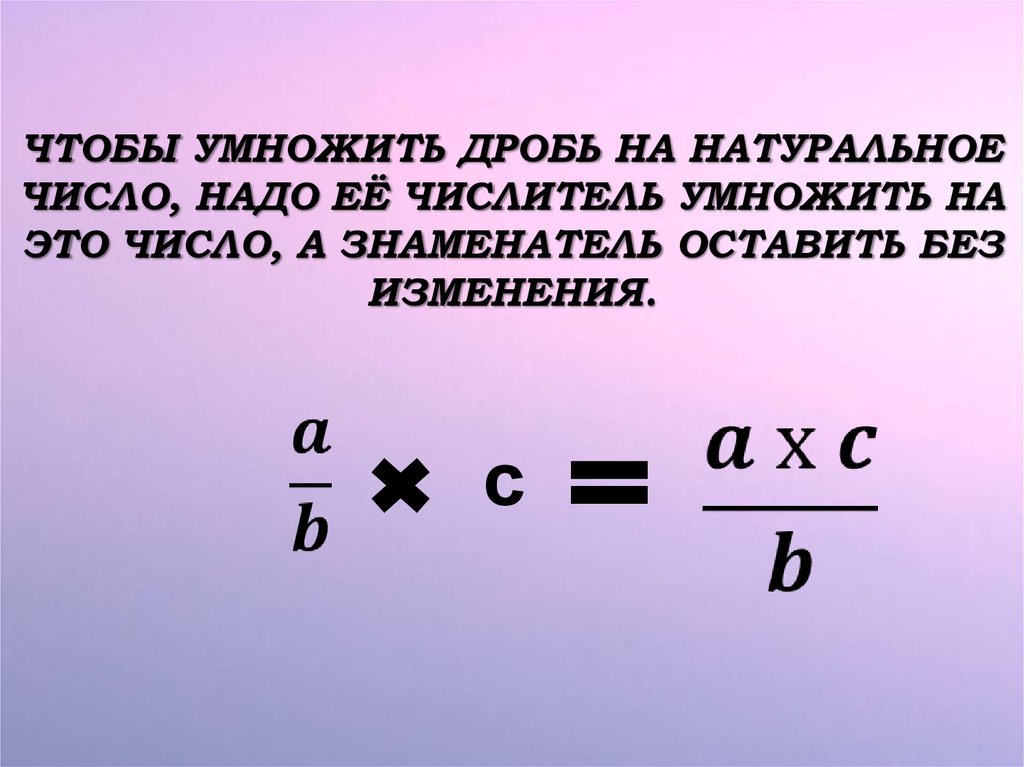




 mathematics
mathematics








