Similar presentations:
Алгоритмы решения задания № 9 «Графики функций»
1. Алгоритмы решения задания № 9 «Графики функций»
Алгоритмы решения задания № 9«Графики функций»
ЕГЭ по математике 2022, профильный уровень
2. Материалы по теме
• https://ege.sdamgia.ru/• https://mat-ege.ru/ege-profile/profile-9-funkcii-i-ih-grafiki/
• https://ege-study.ru/ru/ege/podgotovka/matematika/zadanie-9-ege-pomatematike-grafiki-funkcij/
• https://mathematichka.ru/school/functions/Function_Graph_Table.html
• http://mathprofi.ru/grafiki_i_svoistva_funkcij.html
• https://ege314.ru/9-funktsii-i-ih-svoystva/
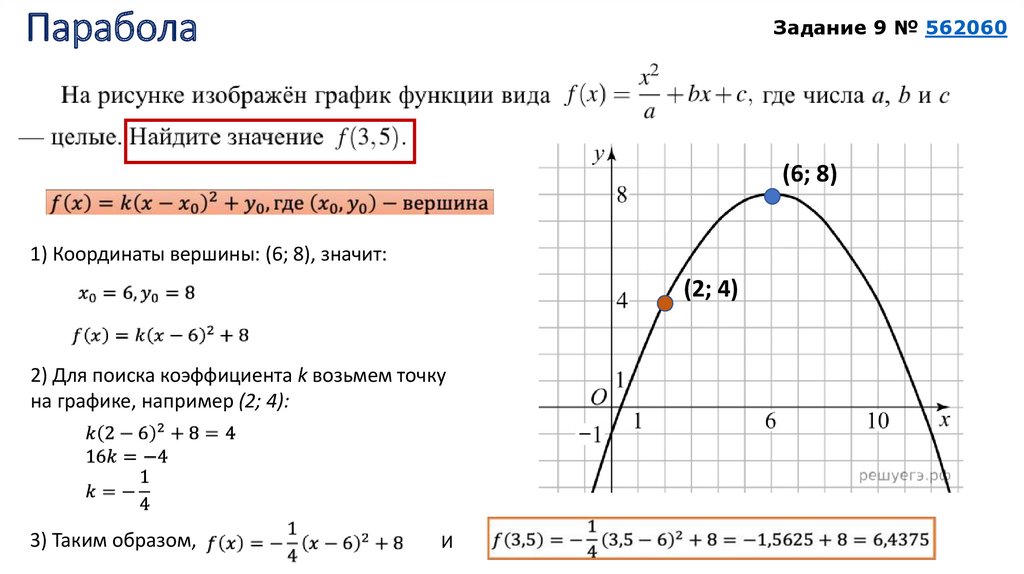
3. Парабола
Задание 9 № 562060(6; 8)
1) Координаты вершины: (6; 8), значит:
(2; 4)
2) Для поиска коэффициента k возьмем точку
на графике, например (2; 4):
3) Таким образом,
И
4. Парабола
Задание 9 № 562283(5; 7)
1)
(3; 3)
2)
3) Таким образом,
И
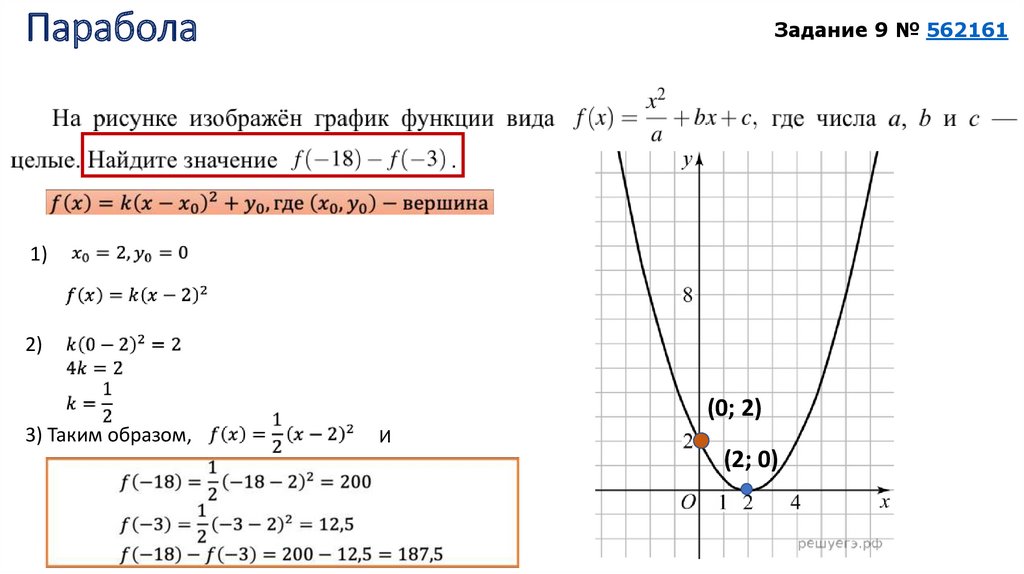
5. Парабола
Задание 9 № 5621611)
2)
(0; 2)
3) Таким образом,
И
(2; 0)
6. Парабола
Задание 9 № 564654(-1; 6)
1) Возьмем координаты трех точек и запишем в виде
Вычтем из (1) (2) и из (2) (3):
(-2; 1)
(-3; -2)
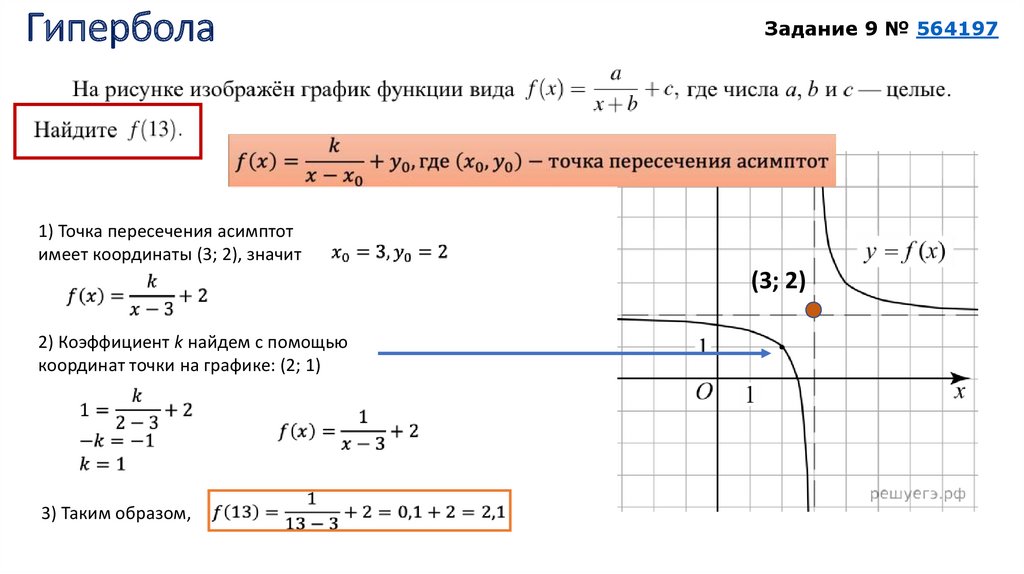
7. Гипербола
Задание 9 № 5641971) Точка пересечения асимптот
имеет координаты (3; 2), значит
(3; 2)
2) Коэффициент k найдем с помощью
координат точки на графике: (2; 1)
3) Таким образом,
8. Гипербола
Задание 9 № 5649722) Коэффициент k найдем с помощью
координат точки на графике: (6; 0)
(5; -1)
3)
Ответ: -3
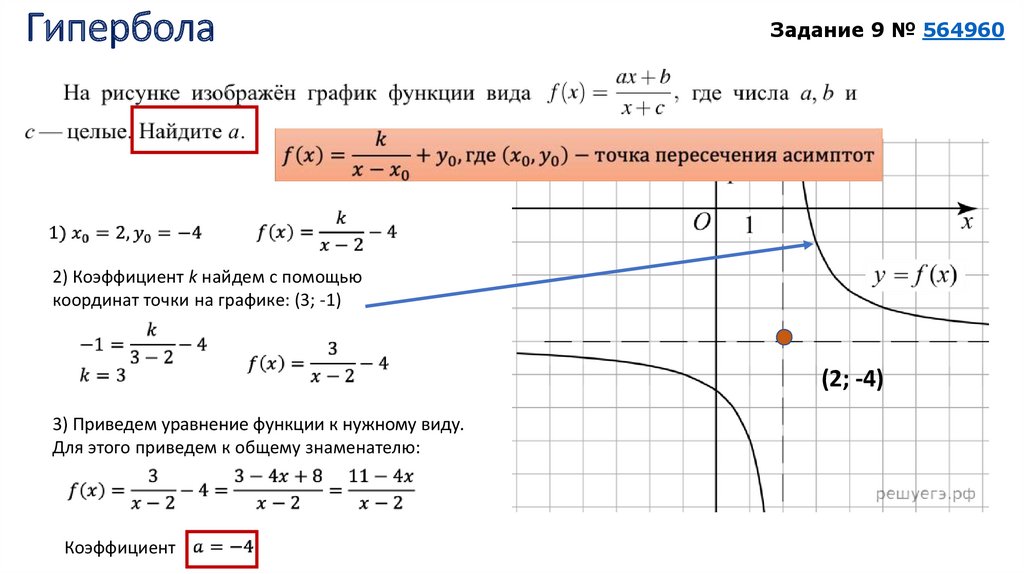
9. Гипербола
Задание 9 № 5649602) Коэффициент k найдем с помощью
координат точки на графике: (3; -1)
(2; -4)
3) Приведем уравнение функции к нужному виду.
Для этого приведем к общему знаменателю:
Коэффициент
10. Гипербола
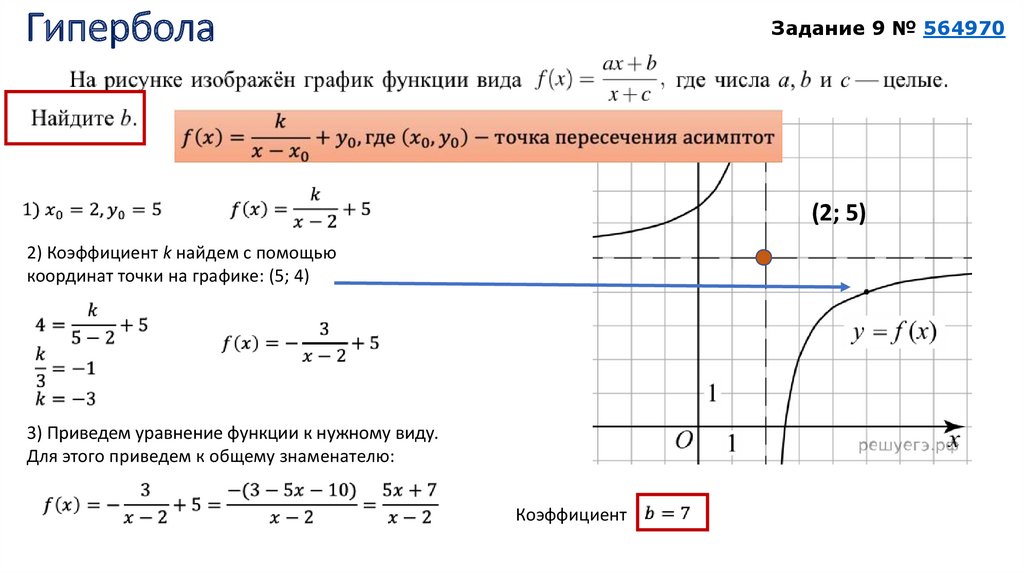
Задание 9 № 564970(2; 5)
2) Коэффициент k найдем с помощью
координат точки на графике: (5; 4)
3) Приведем уравнение функции к нужному виду.
Для этого приведем к общему знаменателю:
Коэффициент
11. Гипербола
Задание 9 № 564966(-2; 2)
12. Показательные функции
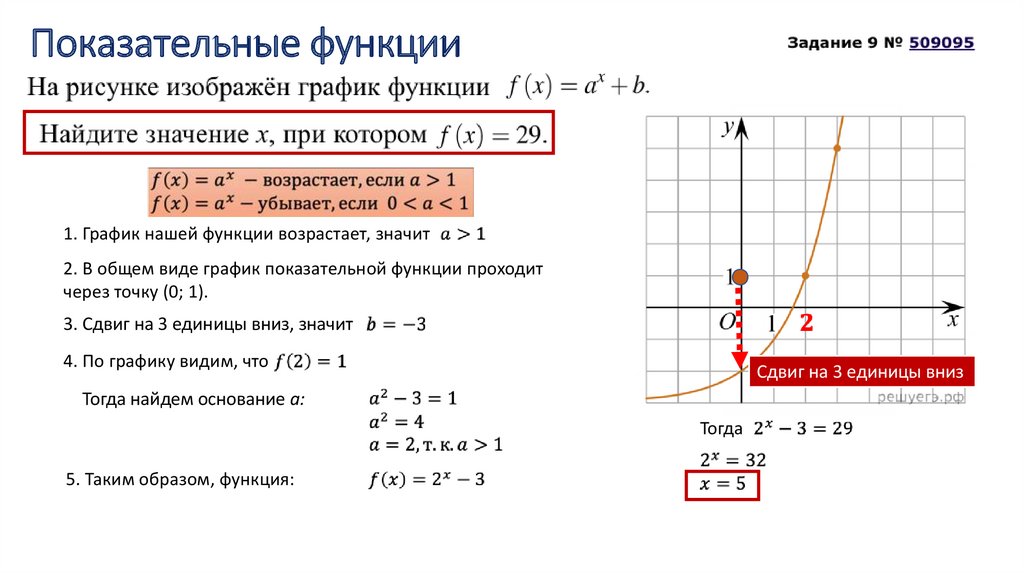
1. График нашей функции возрастает, значит2. В общем виде график показательной функции проходит
через точку (0; 1).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Тогда найдем основание а:
5. Таким образом, функция:
Тогда
Сдвиг на 3 единицы вниз
13. Показательные функции
1. График нашей функции возрастает, значит2. В общем виде график показательной функции проходит
через точку (0; 1).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Сдвиг на 3 единицы вниз
Тогда найдем основание а:
Тогда
5. Таким образом, функция:
14. Показательные функции
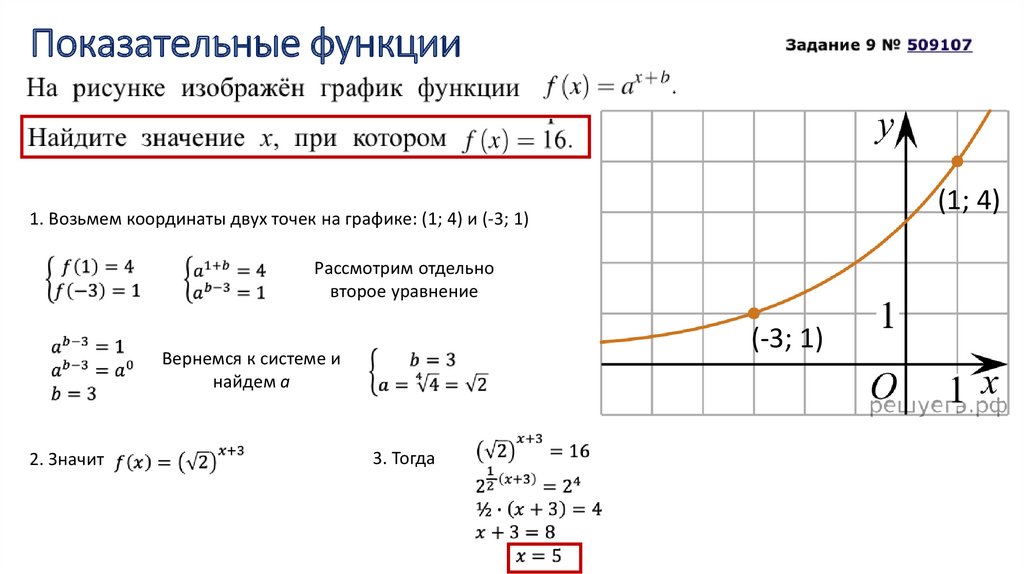
1. Возьмем координаты двух точек на графике: (1; 4) и (-3; 1)(1; 4)
Рассмотрим отдельно
второе уравнение
Вернемся к системе и
найдем a
2. Значит
3. Тогда
(-3; 1)
15. Показательные функции
(1; 4)1. Возьмем координаты двух точек на графике: (1; 4) и (-3; 1)
Рассмотрим отдельно
второе уравнение
(-3; 1)
Вернемся к системе и
найдем a
2. Значит
3. Тогда
16. Логарифмические функции
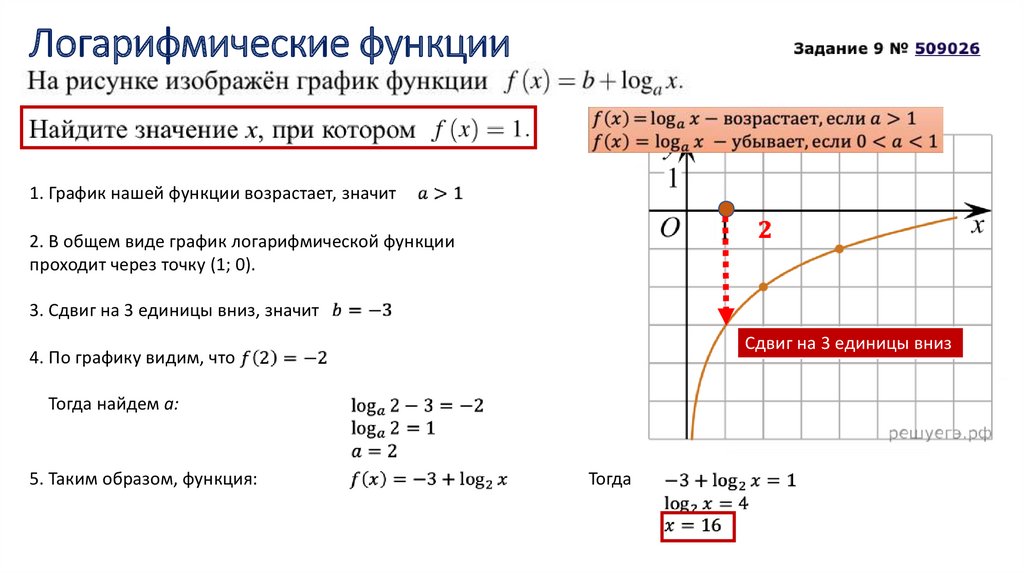
1. График нашей функции возрастает, значит2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 3 единицы вниз, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 3 единицы вниз
17. Логарифмические функции
1. График нашей функции возрастает, значит2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 3 единицы вниз, значит
Сдвиг на 3 единицы вниз
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
18. Логарифмические функции
1. График нашей функции возрастает, значит2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 5 единиц влево, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 5 единиц влево
19. Логарифмические функции
1. График нашей функции возрастает, значит2. В общем виде график логарифмической функции
проходит через точку (1; 0).
3. Сдвиг на 5 единиц влево, значит
4. По графику видим, что
Тогда найдем а:
5. Таким образом, функция:
Тогда
Сдвиг на 5 единиц влево
20.
Линейная функцияЗадание 9 № 508895
Задание 9 № 508903
1)
2)
(3; 4)
7
1)
2)
4
21.
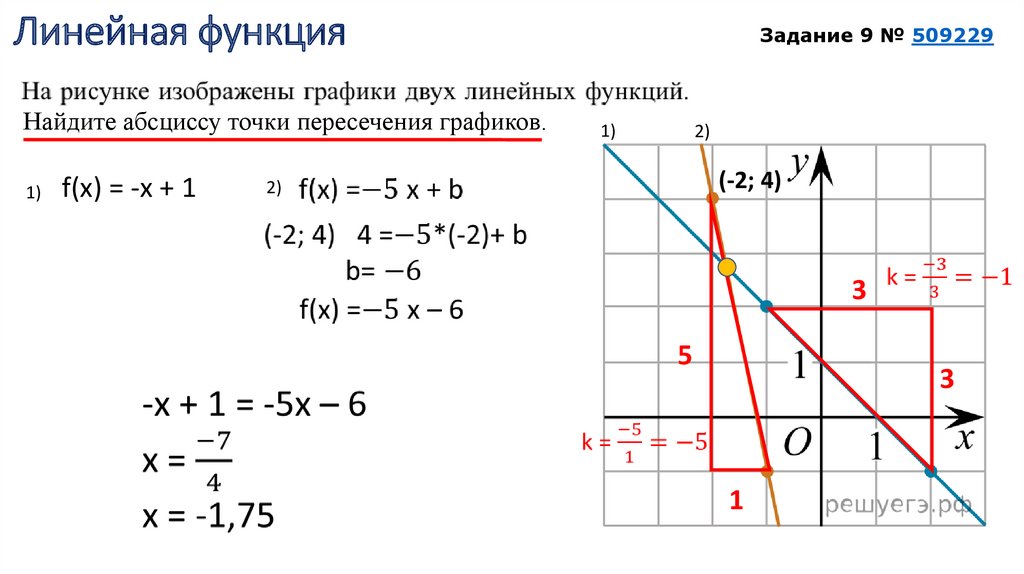
Линейная функцияНайдите абсциссу точки пересечения графиков.
1)
f(x) = -x + 1
Задание 9 № 509229
1)
2)
(-2; 4)
2)
3
5
3
1
22.
Линейная функцияЗадание 9 № 621771
Найдите абсциссу точки пересечения графиков.
2)
f(x) = x + 1
(-2; 4)
3
x + 1 = 1,5 x + 7
0,5x = -6
x = - 12
2
2
2
1)
2)
23.
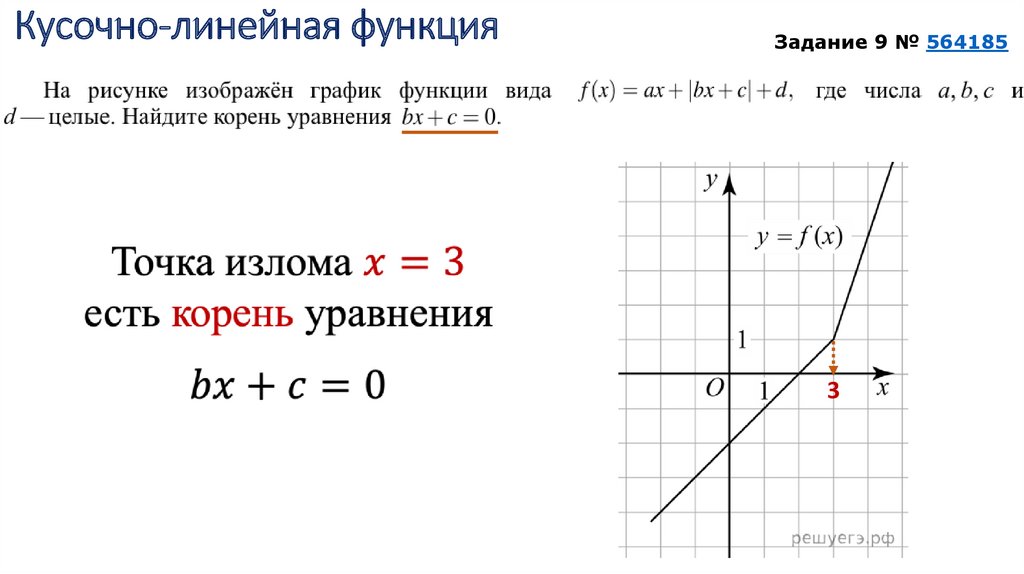
Кусочно-линейная функцияЗадание 9 № 564185
3
24.
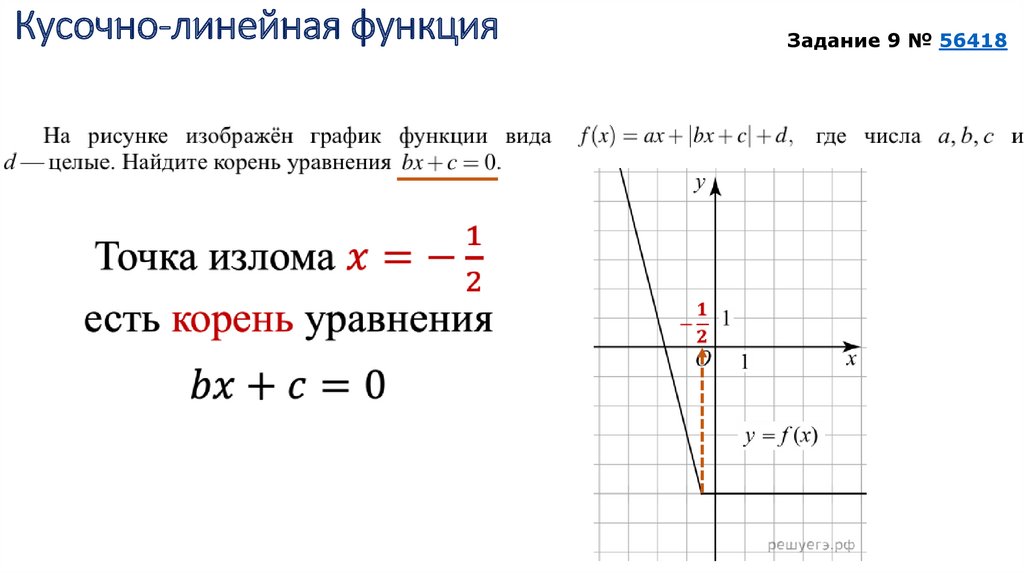
Кусочно-линейная функцияЗадание 9 № 56418
25.
kОпределим, что
m
k
m
26.
Кусочно-линейная функцияЗадание 9 № 563824
1)
1) y = -1x + 3
k=-1; m=3
2) y = 3x - 5
k=3; m=-5
k
a+b = 3
a- b = -1
2a=2
a=1
2)
m
c+d = -5
-c+d = 3
2d=-2
d=-1
2
α
3
2
3
α
1
Справочно:
y = kx + m
k=tgα
1x - 1 = 0
x=1
y = 3x + m
(2;1) 3*2 + m = 1
m=-5
27.
СинусоидыT = 2π
«горка» a > 0
«рост» 2
График симметричен
относительно Oy
28.
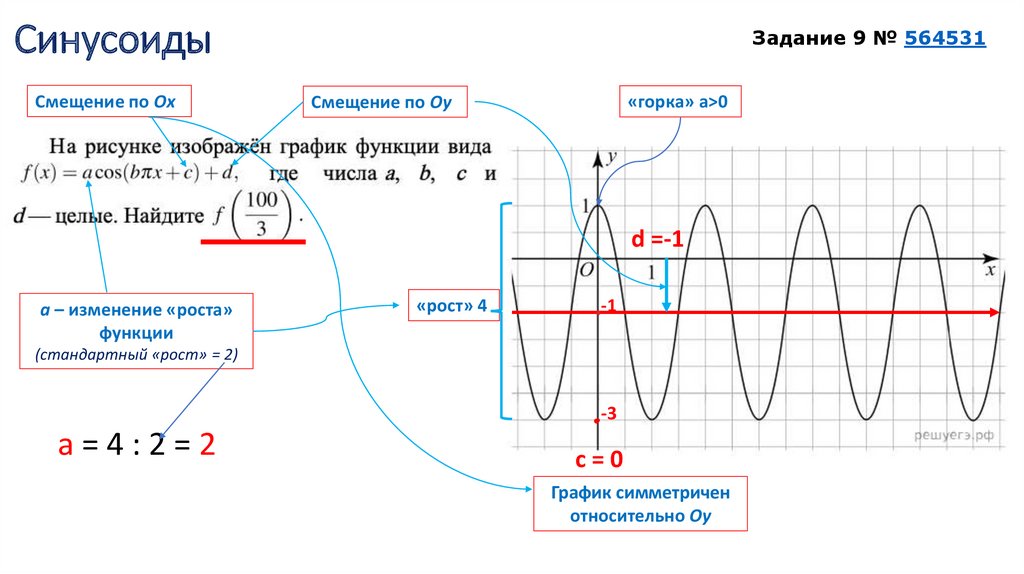
СинусоидыСмещение по Ox
Задание 9 № 564531
«горка» a>0
Смещение по Оу
d =-1
а – изменение «роста»
функции
«рост» 4
-1
(стандартный «рост» = 2)
-3
а=4:2=2
с=0
График симметричен
относительно Oy
29.
T=2f(x) = 2 cos (bπx) - 1
k = bπ;
|b| = 1
f(x) = 2 cos(πx) - 1
30.
СинусоидыЗадание 9 № 564589
T=1
а = -2 : 2 = -1
d =-1
|b| = 2
«рост» 2
f(x) = -cos (2πx) - 1
-2
с=0
«ямка»
а<0
31.
СинусоидыНа
рисунке
Задание 9 № 564556
изображён
график
функции
вида
где
«горка» a>0
T=4
числа a, b, c и d — целые. Найдите
4
а=4:2=2
|b| = 2
«рост» 4
2
с=0
d=2
32. Благодарим за внимание!
Белова Марина Александровнаbelova_ma@school509.spb.ru
Каратун Ольга Леонтьевна
karatun_ol@school509.spb.ru




















 mathematics
mathematics








