Функция у=х2 её свойства и график. Что такое функция?

1. Функция у=х2 её свойства и график

Наш девиз: «Дорогу осилит
идущий,
а математику - мыслящий

2. Цели:

• Познакомиться с новой функцией y = x2;
её свойствами ; научиться строить график
этой функции;
• воспитывать в себе аккуратность,

3. Вспомним, что проходили

1)Что такое функция?
2)Функция какого вида
называется линейной?
3)Что является графиком
линейной функции?
4)Что означает возвести в квадрат?
5)Что такое абсцисса, ордината?
6)Что такое аргумент?
7)Как называют зависимую переменную?

4.

• Функция – это зависимость переменной у
от х, если каждому х соответствует только
одно у.
• Линейная функция у = кх+m
• график линейной функции – прямая
• Возвести в квадрат- число умножить само
2
на себя х х х
• Абсцисса –это х ордината – это у
• Аргумент - независимая переменная
• зависимая переменная – это у
ВСПОМНИЛИ?
МОЛОДЦЫ!

5.

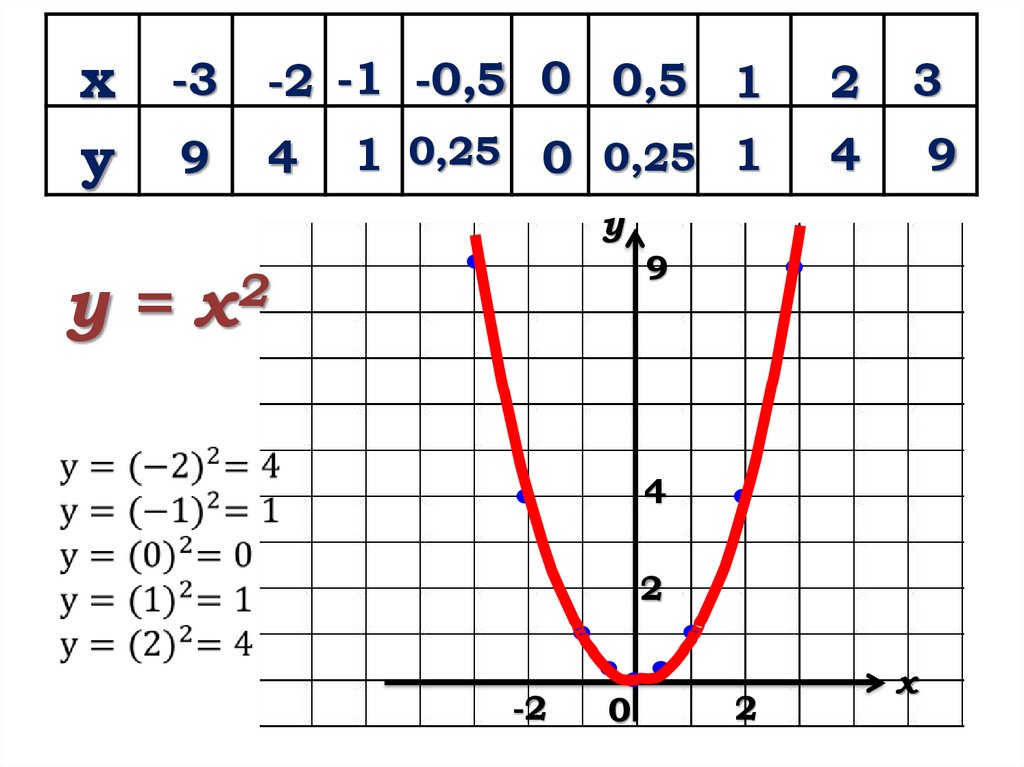
х -3 -2 -1 -0,5 0 0,5 1
у 9 4 1 0,25 0 0,25 1
2
3
4
9
у
у=
9
2
х
4
2
-2
0
2
х

6.

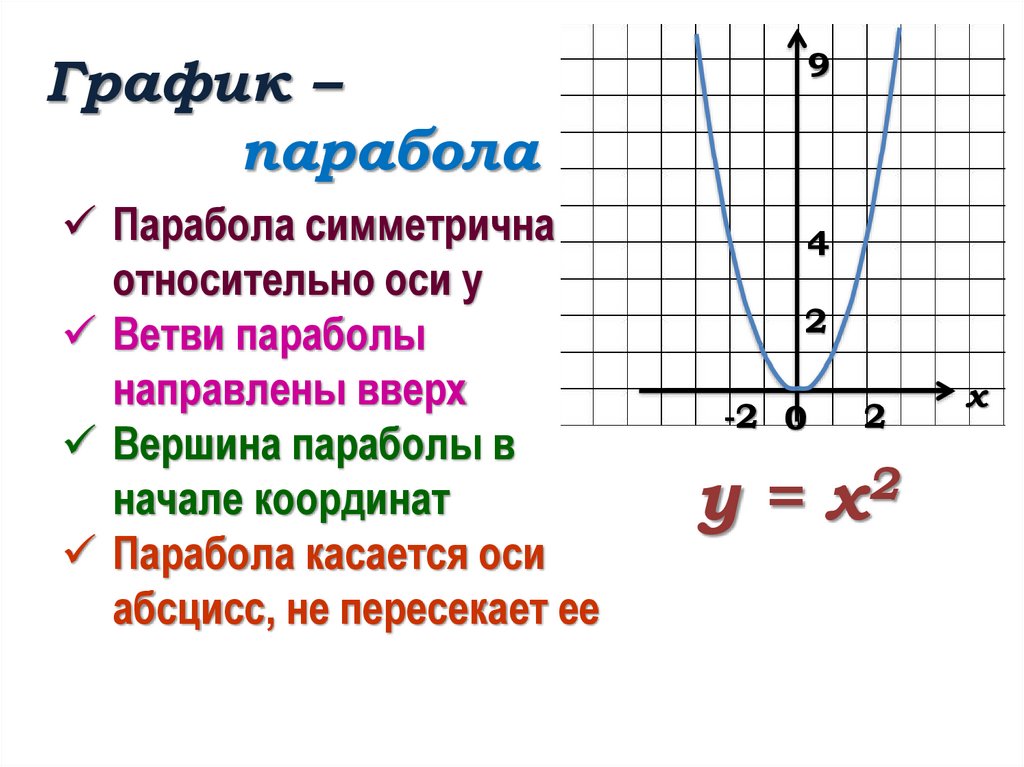
9
График –
парабола
Парабола симметрична
относительно оси у
Ветви параболы
направлены вверх
Вершина параболы в
начале координат
Парабола касается оси
абсцисс, не пересекает ее
4
2
-2 0
у=
2
2
х
х

7.

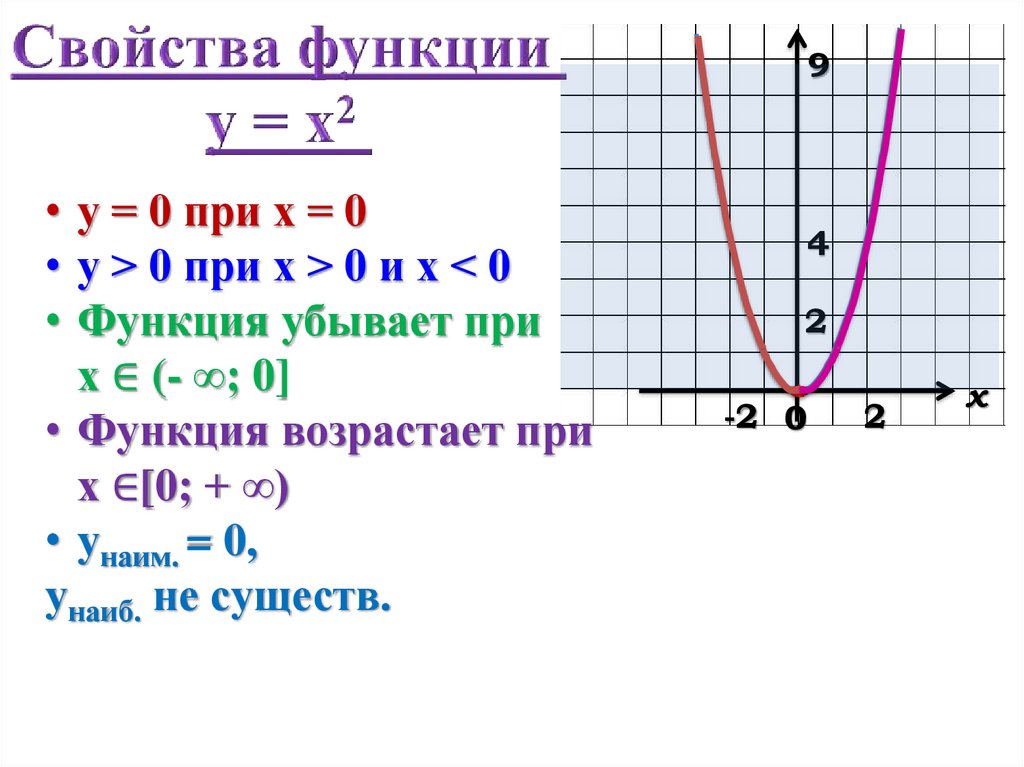
9
• у = 0 при х = 0
• у > 0 при х > 0 и х < 0
• Функция убывает при
х ∈ (- ∞; 0]
• Функция возрастает при
х ∈[0; + ∞)
• унаим. = 0,
унаиб. не существ.
4
2
-2 0
2
х

8.

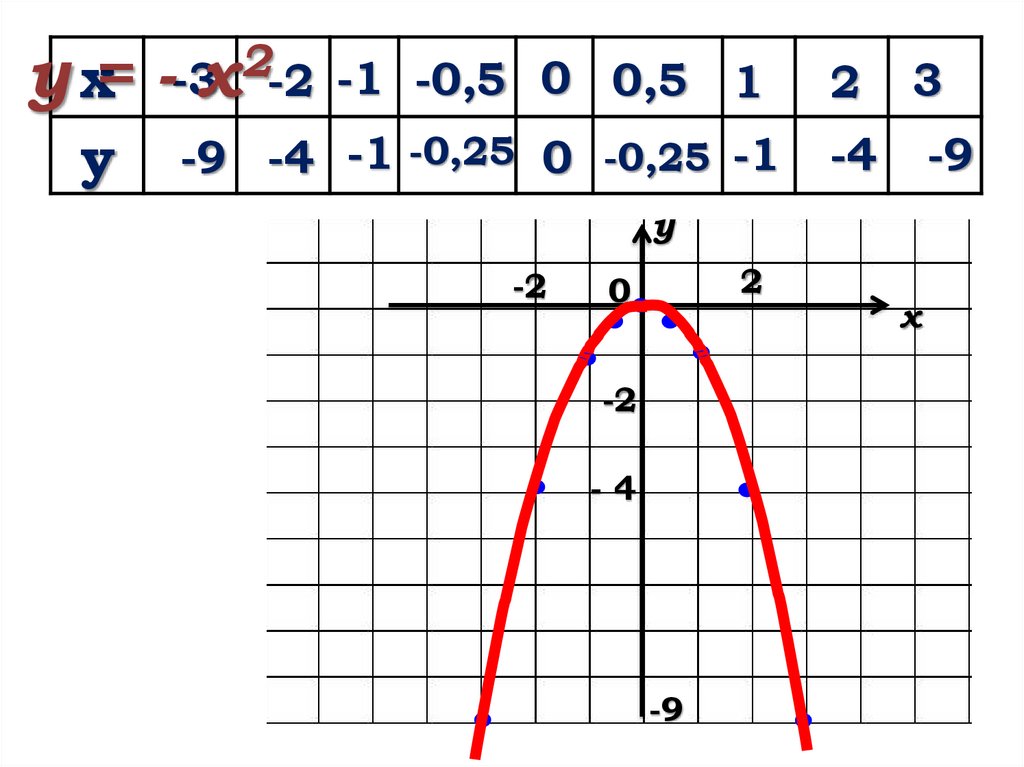
у х=
у
2
-3
- х -2 -1 -0,5 0 0,5 1
-9 -4 -1 -0,25 0 -0,25 -1
2
3
-4
-9
у
-2
2
0
-2
-4
-9
х

9.

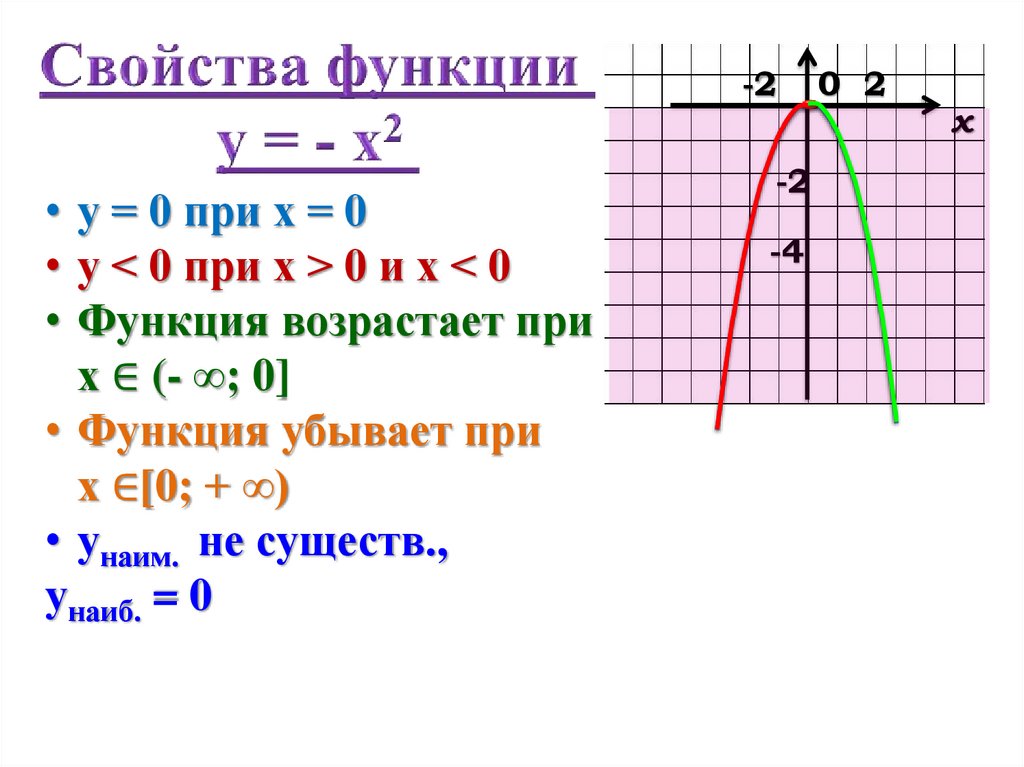
-2
• у = 0 при х = 0
• у < 0 при х > 0 и х < 0
• Функция возрастает при
х ∈ (- ∞; 0]
• Функция убывает при
х ∈[0; + ∞)
• унаим. не существ.,
унаиб. = 0
-2
-4
0 2
х

10. Практическое Применение параболы

11. Парабола в архитектуре и строительстве

Форма параболы используется в архитектуре
для строительства крыш и куполов

12.

13. Парабола в природе

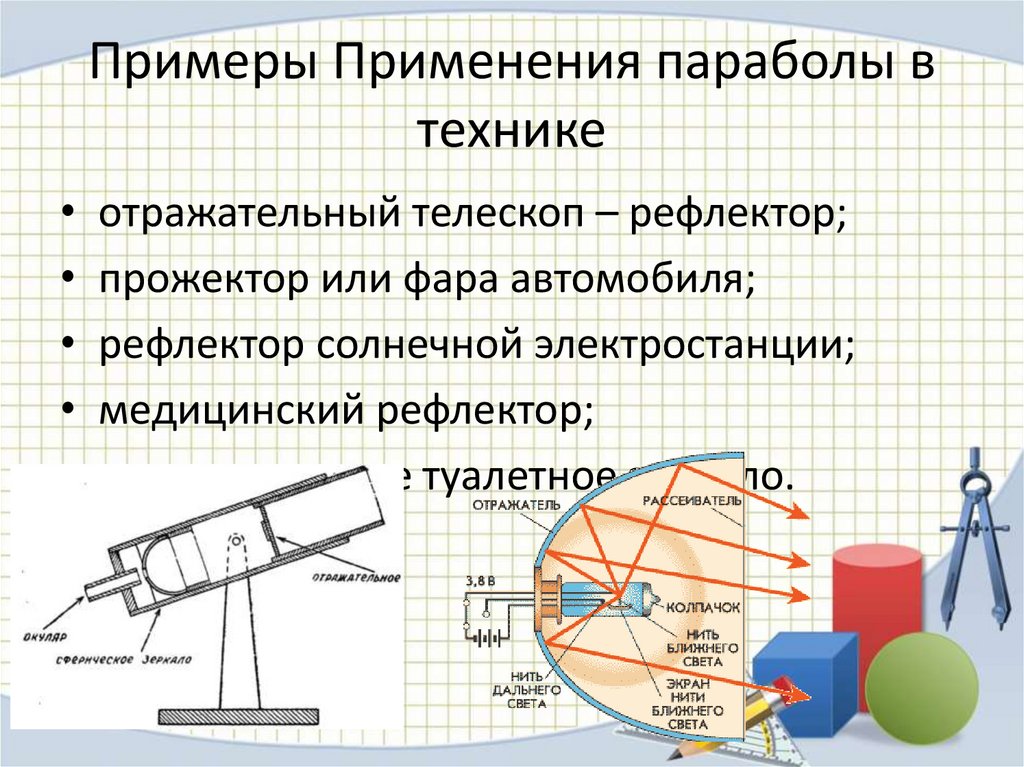
14. Примеры Применения параболы в технике

отражательный телескоп – рефлектор;
прожектор или фара автомобиля;
рефлектор солнечной электростанции;
медицинский рефлектор;
увеличительное туалетное зеркало.

15.

16.

33.8(а), 33.9(а)
+
Теорию записать
в тетрадь