Similar presentations:
Применение аксиом
1. 22.09.20 г.
Применение аксиом и ихследствий.
2. Итак, что же определяет плоскость?
3.
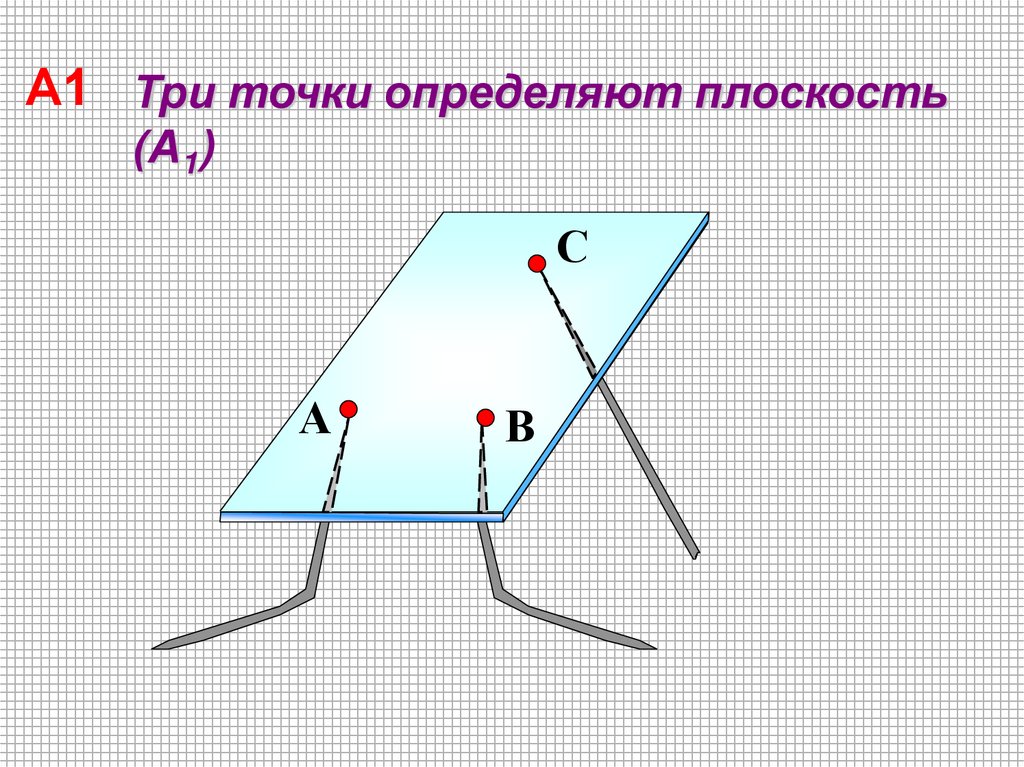
А1 Три точки определяют плоскость(А1)
С
А
В
4.
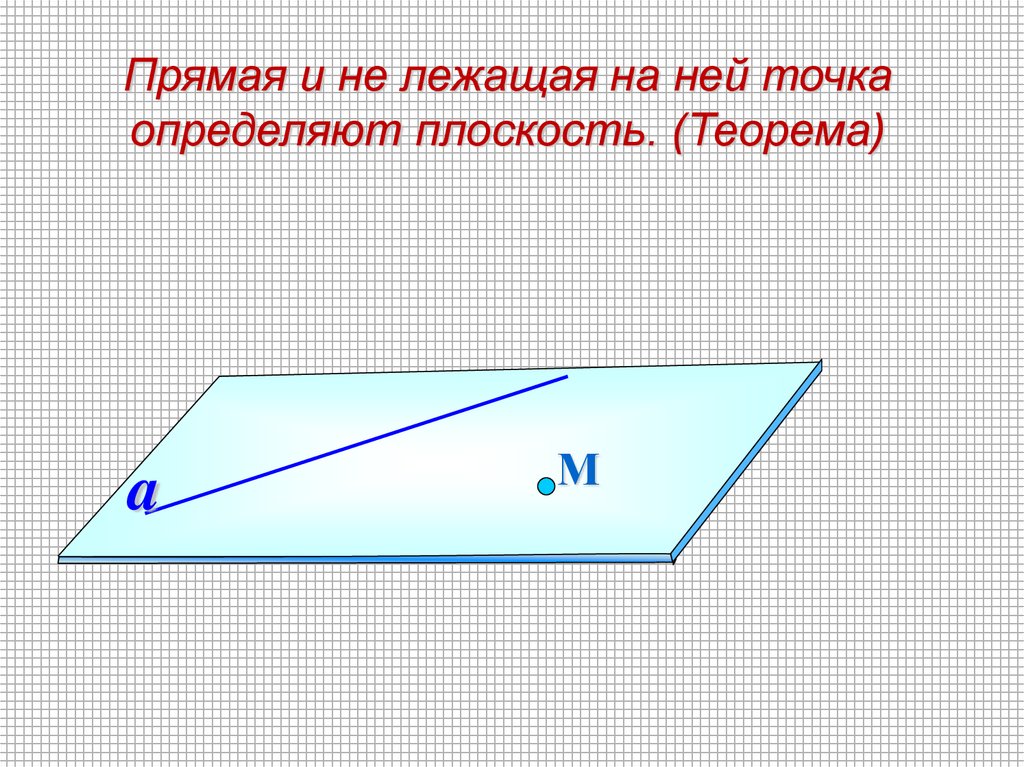
Прямая и не лежащая на ней точкаопределяют плоскость. (Теорема)
a
М
5.
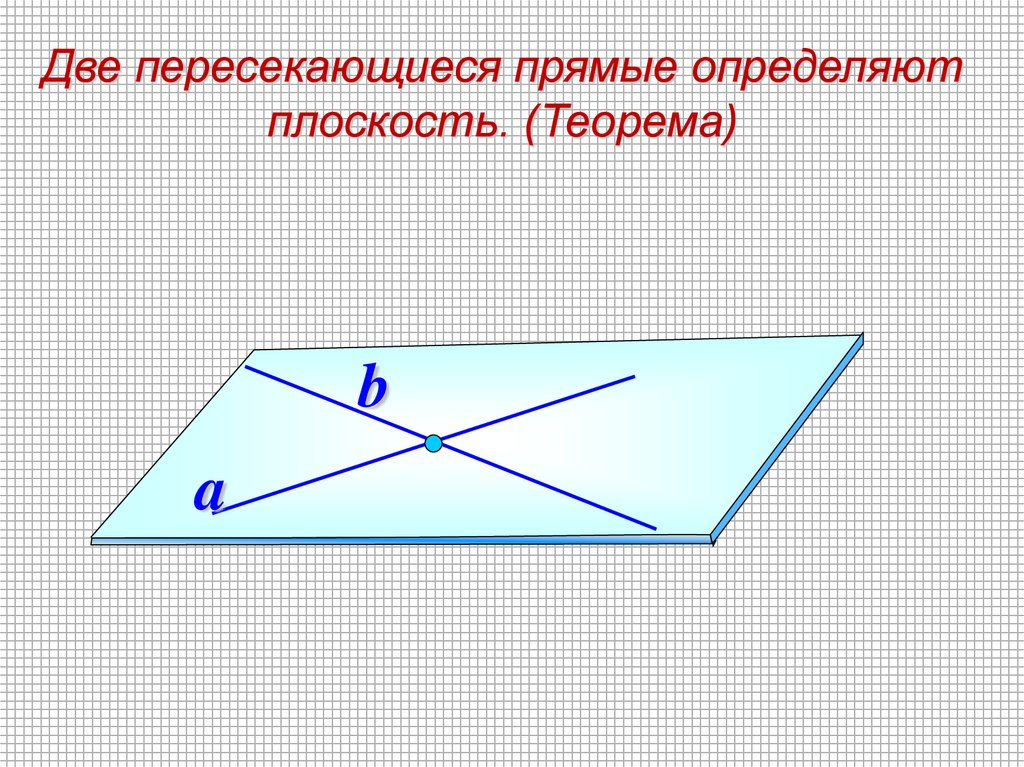
Две пересекающиеся прямые определяютплоскость. (Теорема)
b
a
6.
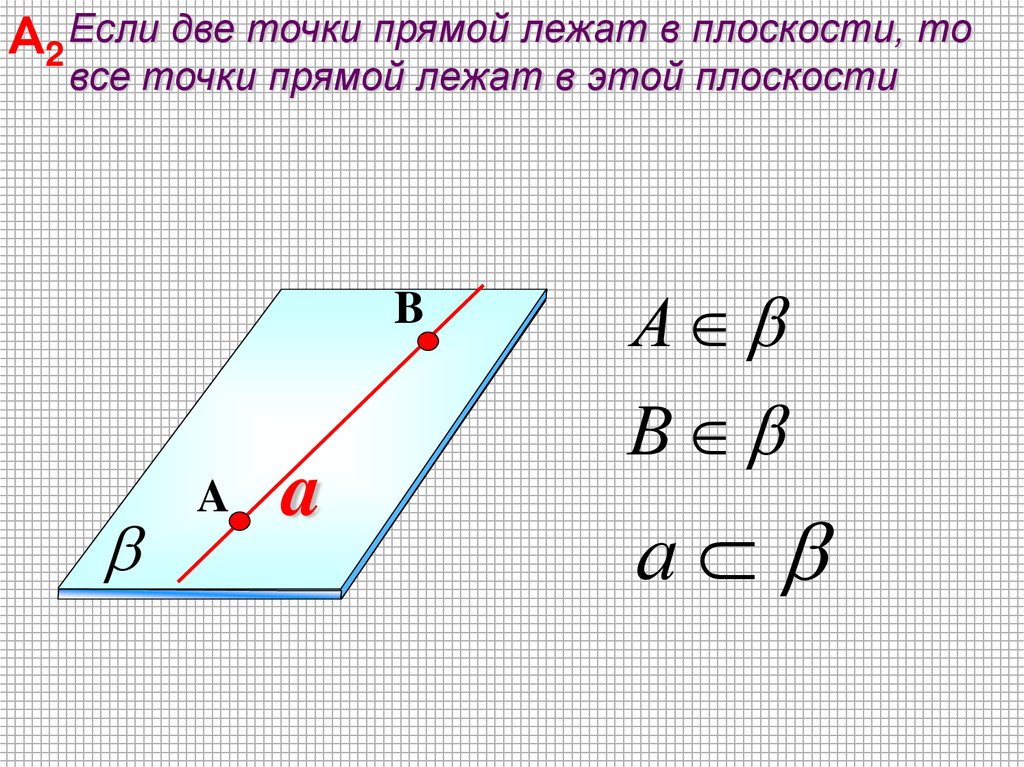
А2 Если две точки прямой лежат в плоскости, товсе точки прямой лежат в этой плоскости
B
A
a
А
В
а
7.
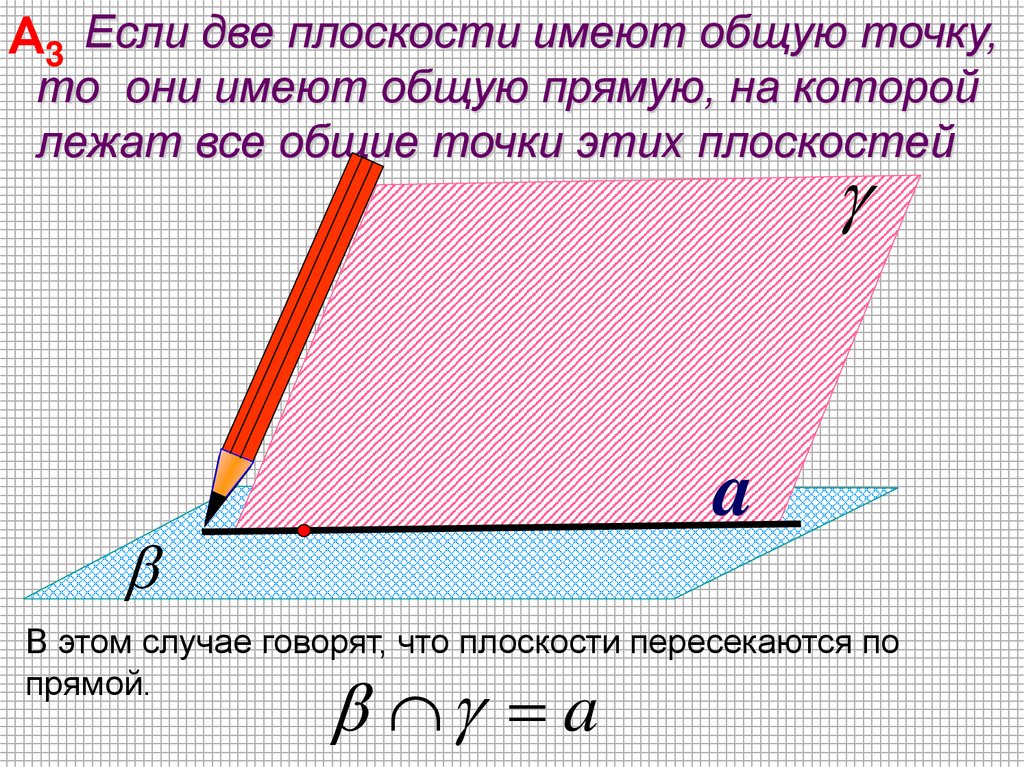
А3 Если две плоскости имеют общую точку,то они имеют общую прямую, на которой
лежат все общие точки этих плоскостей
a
В этом случае говорят, что плоскости пересекаются по
прямой.
a
8.
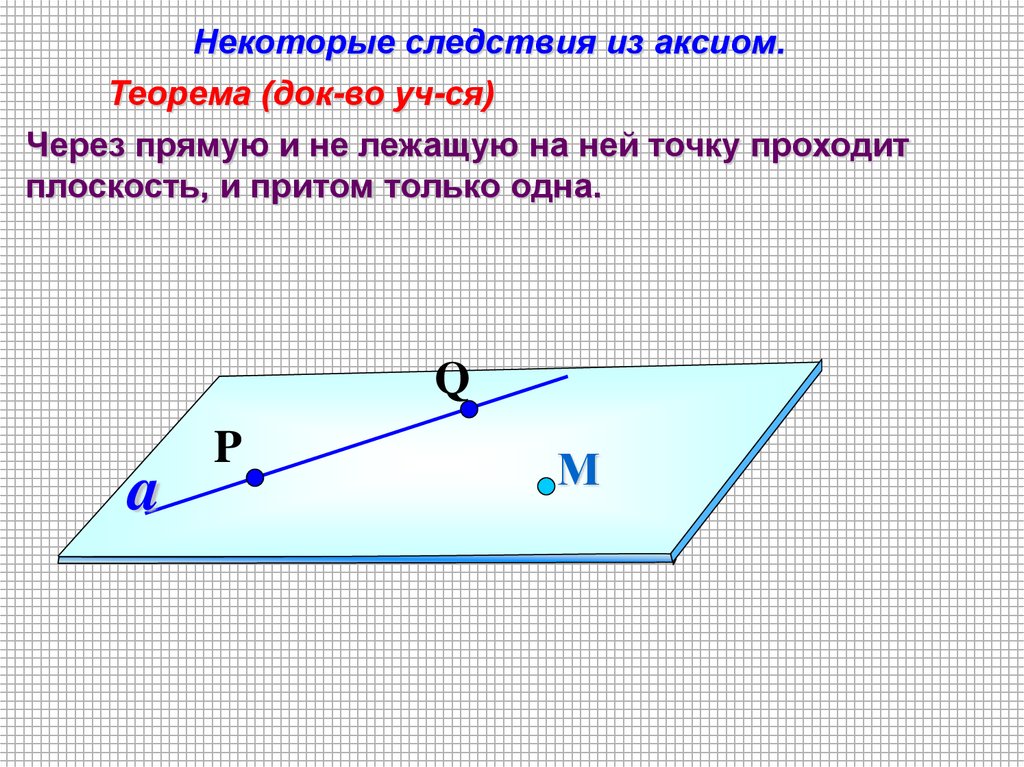
Некоторые следствия из аксиом.Теорема (док-во уч-ся)
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М
9.
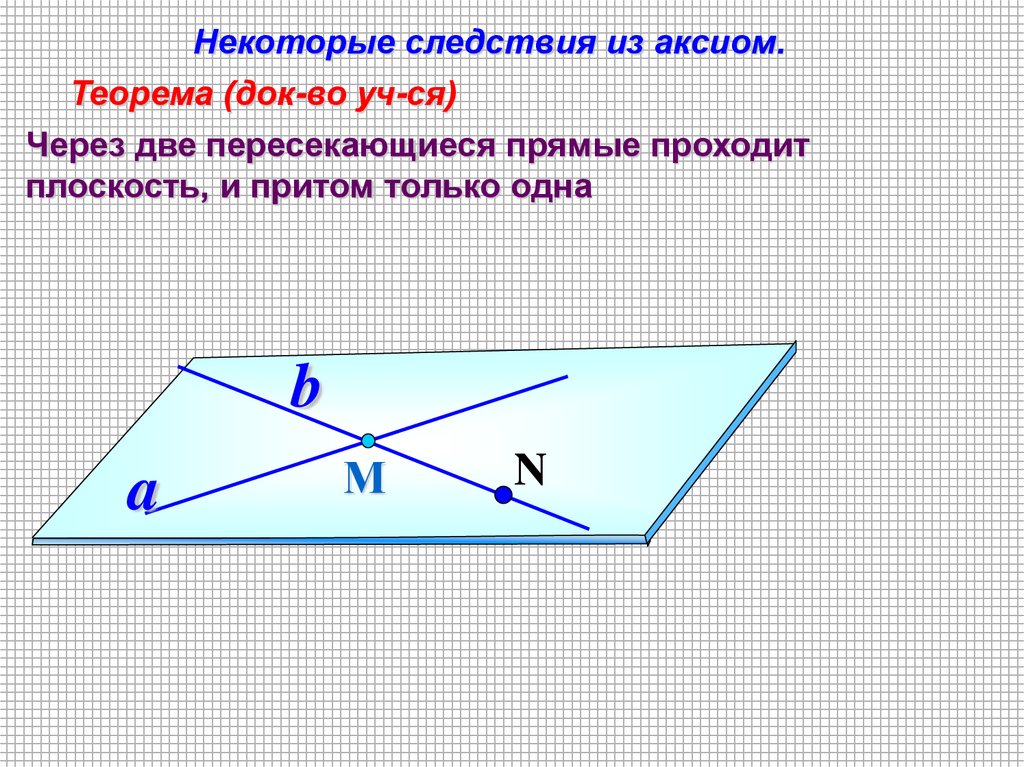
Некоторые следствия из аксиом.Теорема (док-во уч-ся)
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N
10.
МО
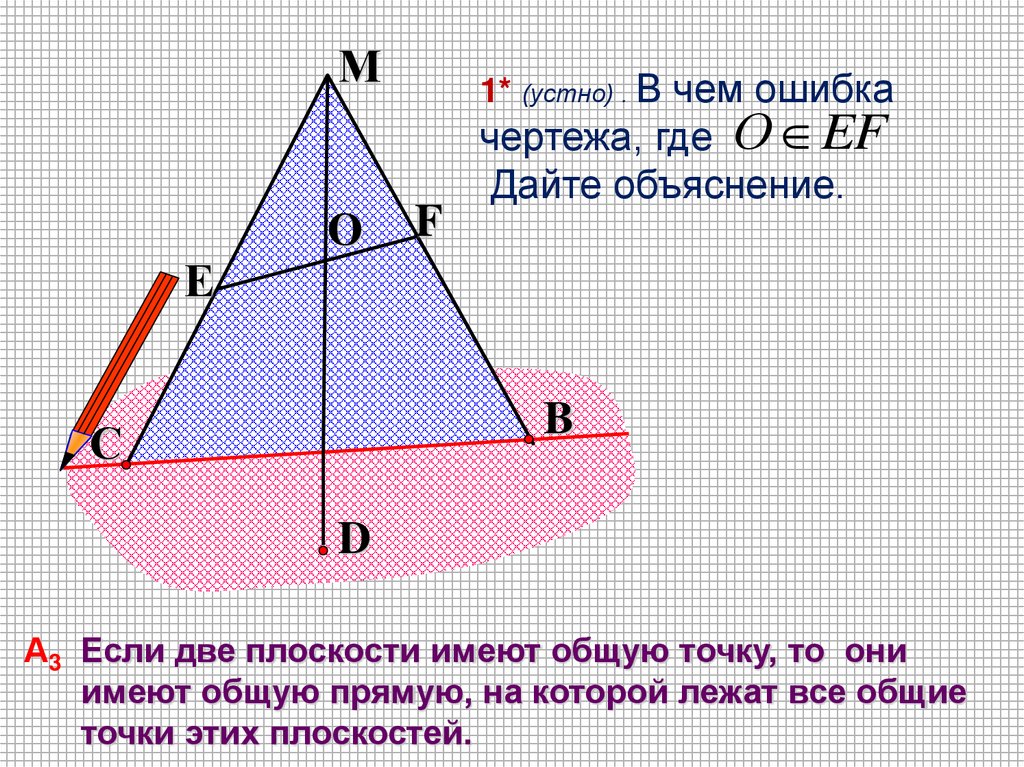
1* (устно) . В чем ошибка
F
чертежа, где О EF
Дайте объяснение.
Е
B
С
D
А3 Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
11.
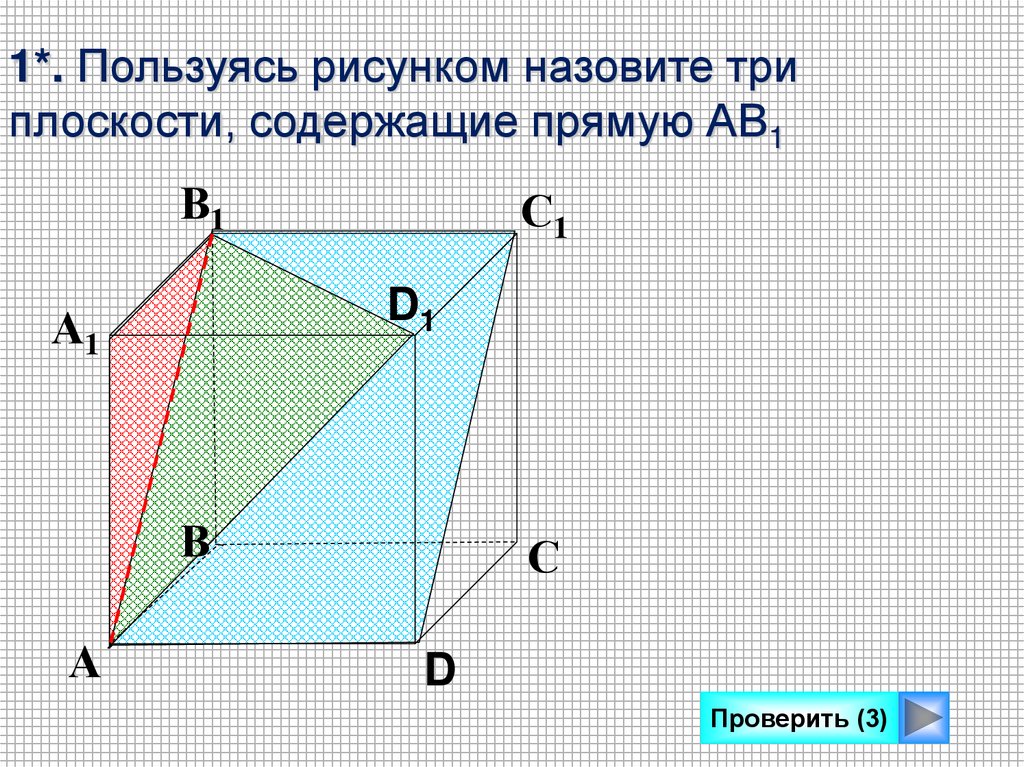
1*. Пользуясь рисунком назовите триплоскости, содержащие прямую АВ1
В1
С1
D1
А1
В
А
С
D
Проверить (3)
12.
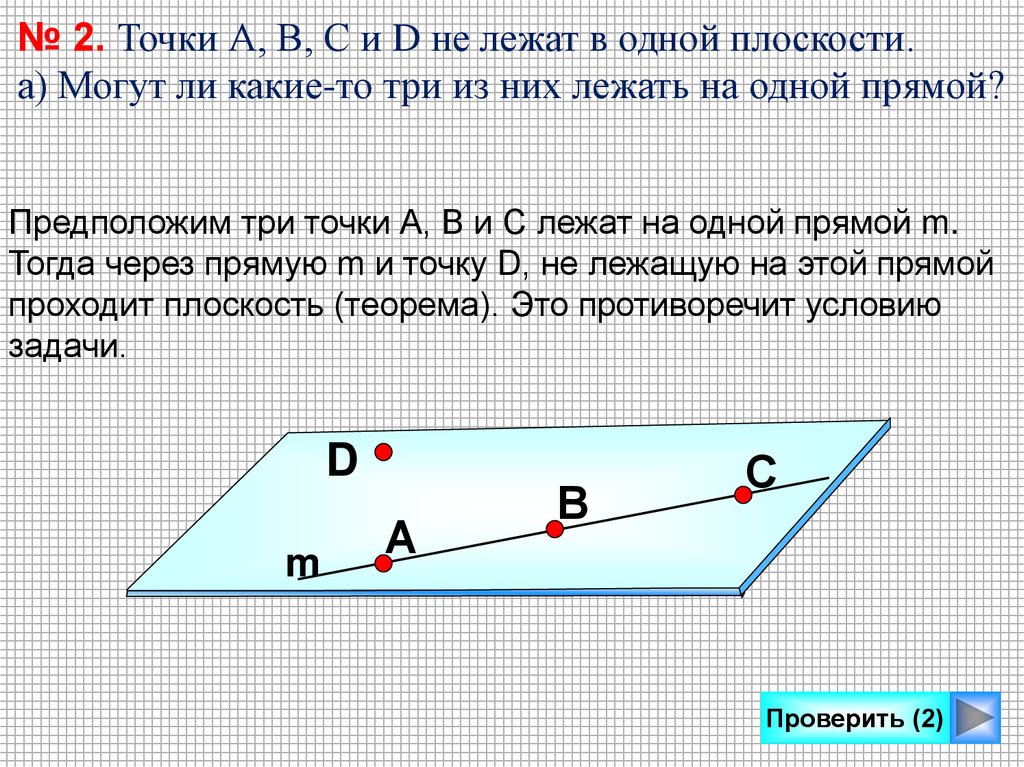
№ 2. Точки А, В, С и D не лежат в одной плоскости.а) Могут ли какие-то три из них лежать на одной прямой?
Предположим три точки А, В и С лежат на одной прямой m.
Тогда через прямую m и точку D, не лежащую на этой прямой
проходит плоскость (теорема). Это противоречит условию
задачи.
D
m
А
В
С
Проверить (2)12
13.
№ 2. Точки А, В, С и D не лежат в одной плоскости.б) Могут ли прямые АВ и СD пересекаться?
Ответ обоснуйте.
Предположим прямые АВ и СD пересекаются.
Тогда через две пересекающиеся прямые проходит плоскость
(теорема). Это противоречит условию задачи.
D
В
А
С
Проверить (2)13
14.
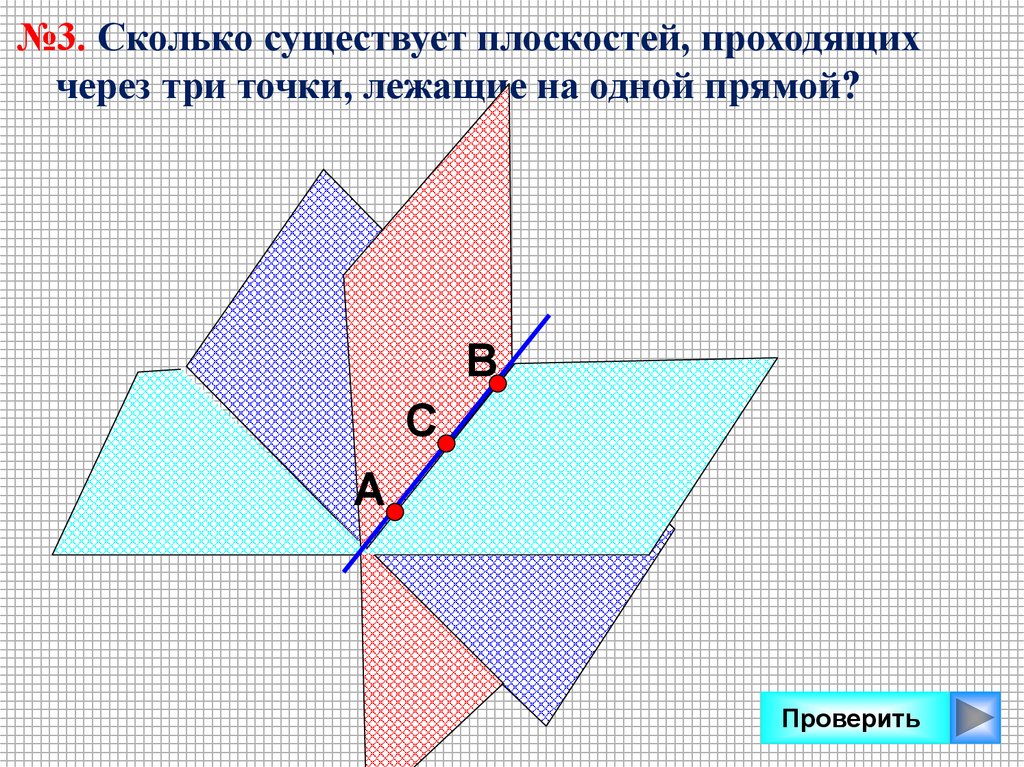
№3. Сколько существует плоскостей, проходящихчерез три точки, лежащие на одной прямой?
В
С
А
Проверить
14
15.
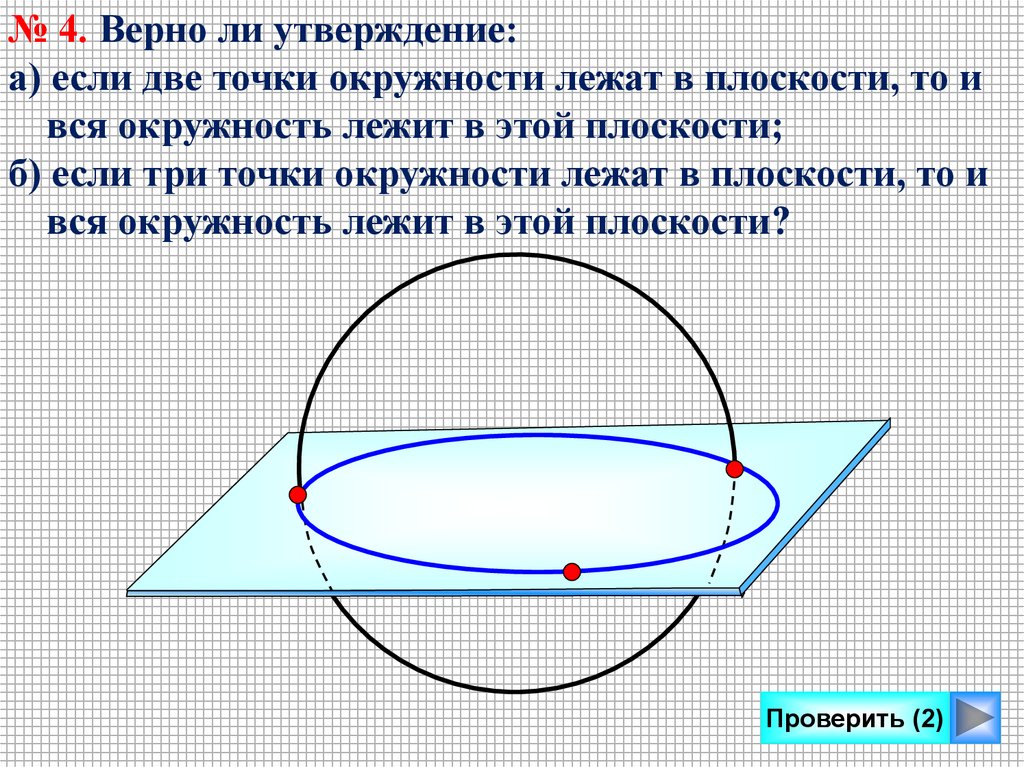
№ 4. Верно ли утверждение:а) если две точки окружности лежат в плоскости, то и
вся окружность лежит в этой плоскости;
б) если три точки окружности лежат в плоскости, то и
вся окружность лежит в этой плоскости?
Проверить (2)15
16.
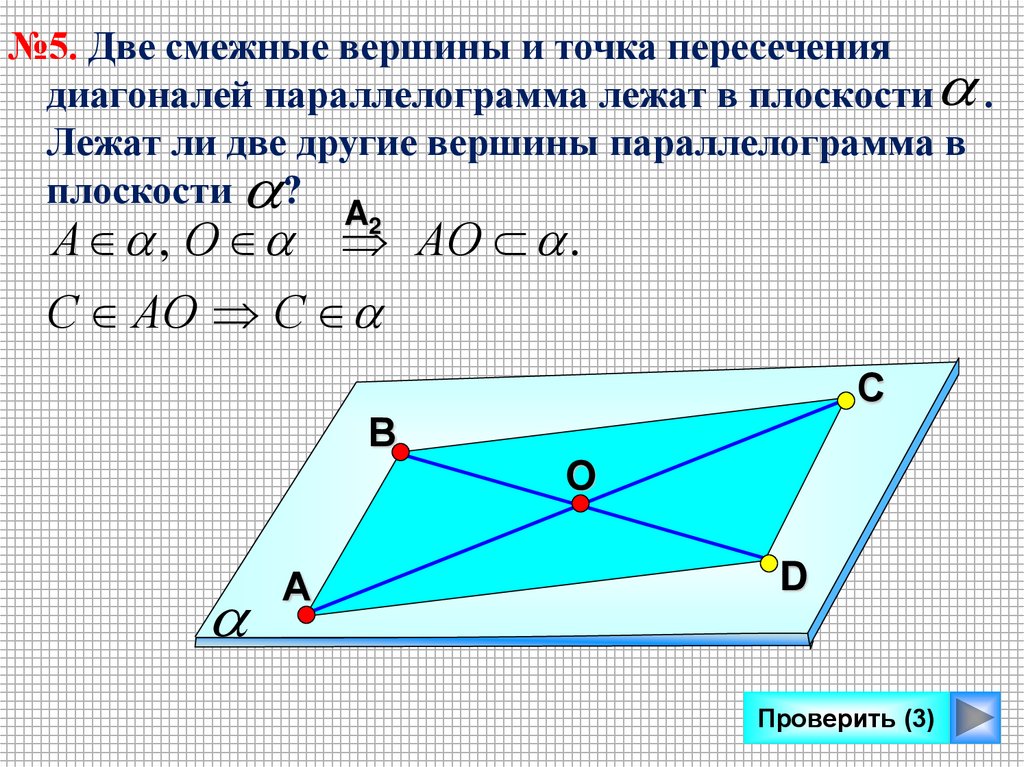
№5. Две смежные вершины и точка пересечениядиагоналей параллелограмма лежат в плоскости .
Лежат ли две другие вершины параллелограмма в
плоскости ?
A2
А , О АО .
С АО С
С
В
O
А
D
Проверить (3) 16
17.
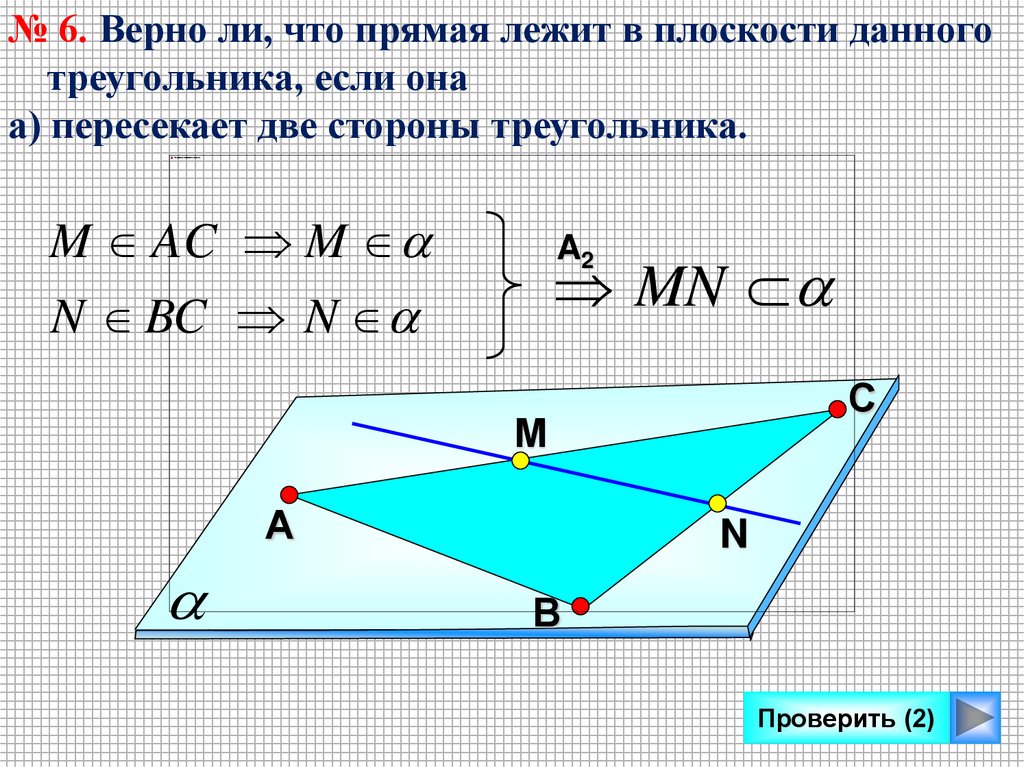
№ 6. Верно ли, что прямая лежит в плоскости данноготреугольника, если она
а) пересекает две стороны треугольника.
M AC M
A2
MN
N BC N
С
М
А
N
В
Проверить (2) 17
18.
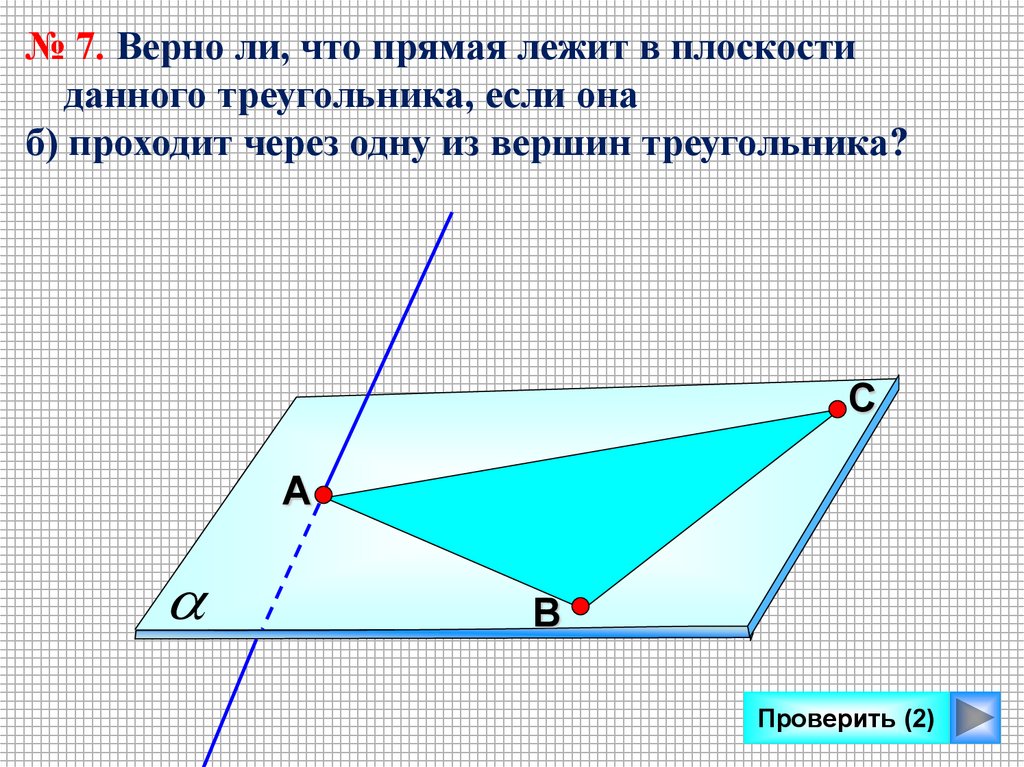
№ 7. Верно ли, что прямая лежит в плоскостиданного треугольника, если она
б) проходит через одну из вершин треугольника?
С
А
В
Проверить (2) 18
19.
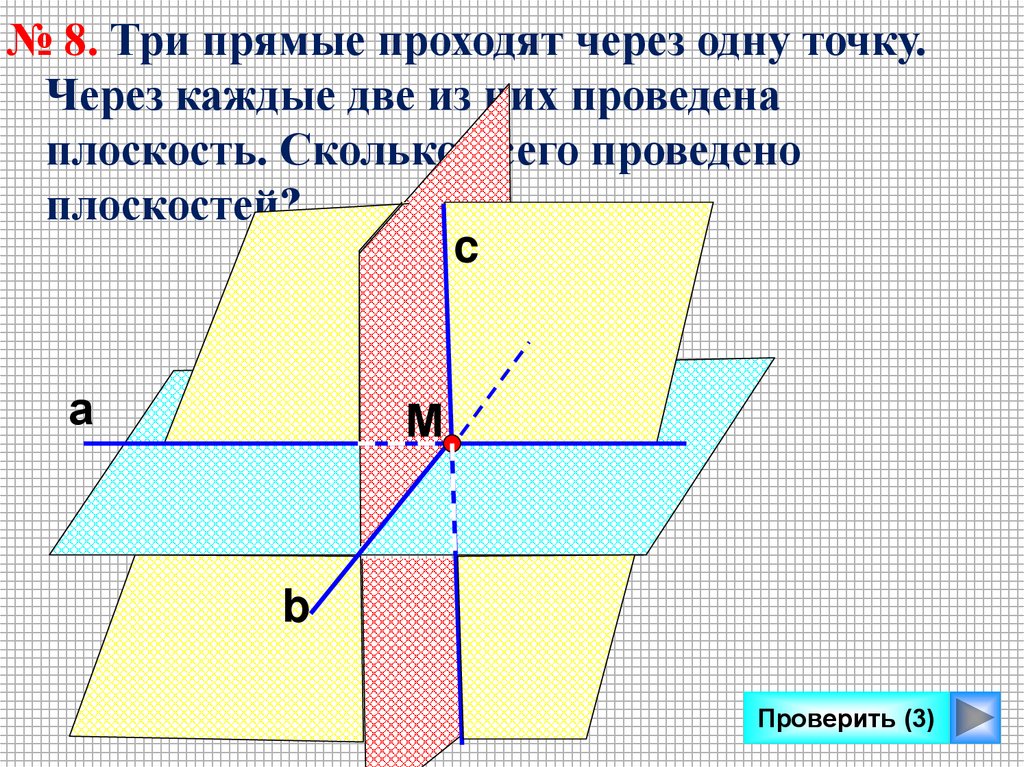
№ 8. Три прямые проходят через одну точку.Через каждые две из них проведена
плоскость. Сколько всего проведено
плоскостей?
c
а
М
b
Проверить (3) 19
20.
D1А1
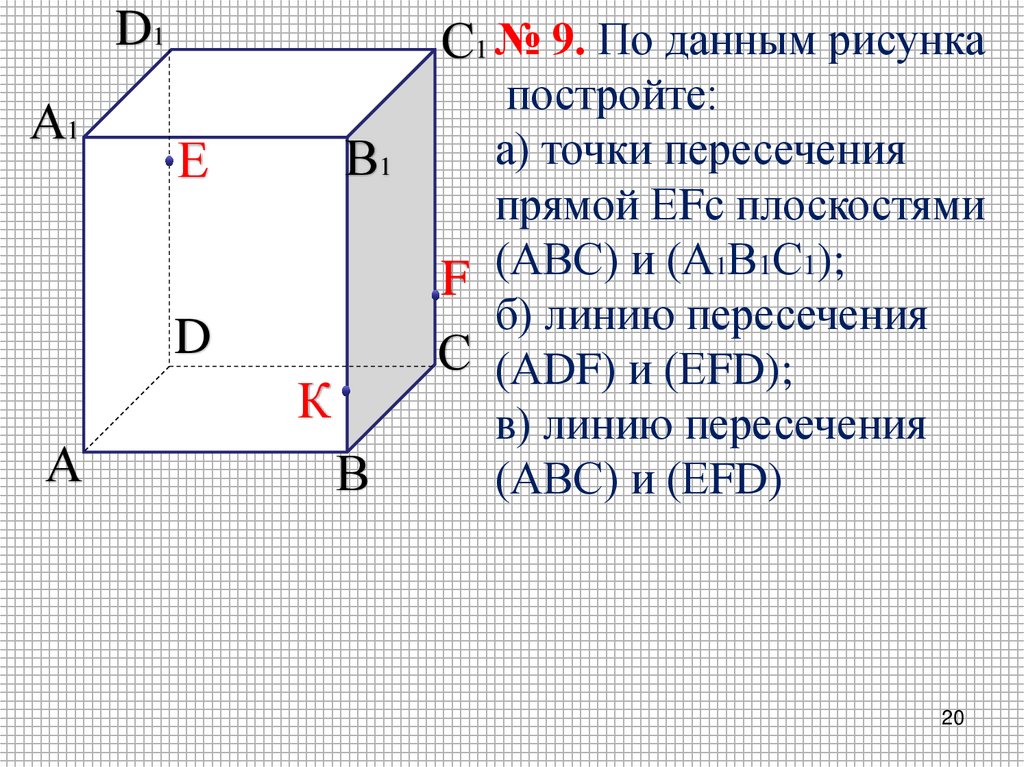
С1 № 9. По данным рисунка
В1
Е
D
К
А
В
постройте:
а) точки пересечения
прямой ЕFс плоскостями
F (АВС) и (А1В1С1);
б) линию пересечения
С (АDF) и (ЕFD);
в) линию пересечения
(АВС) и (ЕFD)
20
21.
На уроке:1) Опрос по А1-А3 и следствиям из них
2) 1* - 10*
3) Повт. тест – 10 минут
4) С/р – 12 минут
Дома:
1) п.1 - 3
2) №7, 13, 1*, 2*
1*. Док-те, что все вершины четырёхугольника лежат в одной
плоскости, если его диагонали пересекаются.
2*. Вычислите площадь четырёхугольника, если АС и ВД
перпендикулярны, АС=10см, СД=12 см.




 mathematics
mathematics