Similar presentations:
Применение аксиом стереометрии
1.
Применениеаксиом
стериометрии
2.
Решить задачу: №1а) плоскости, в которых лежат
прямые РЕ, МК, DВ, АВ, ЕС.
D
а) РЕ (ABD)
МК (BCD)
DВ (ABD); DB (BCD)
АВ (ABD); AB (ABC)
ЕС (ABC)
К
Р
А
М
Е
В
С
б) точки пересечения прямой
DK с плоскостью АВС;
Прямой СЕ с плоскостью ADB.
б) DK (ABC)=C
CE (ADB)= E
3.
Решить задачу: №1в) точки, лежащие в
плоскостях ADB и DBC.
D
в)A, B, D, Е, М, Р (ADB)
В, С, D, К, М (DBC)
(ADB) (DBC) =DB
B, D, M (ADB) и (DBC)
К
Р
А
М
Е
В
С
г) прямые, по которым
пересекаются плоскости
АВС и DCB;
ABD и CDA;
PDC и ABC.
г) АВС DCB = BC;
ABD CDA = AD;
PDC ABC = EC.
4.
Решить задачу: №2В1
Q
С1
P
А1
а) точки, лежащие в
плоскостях DCC1 и BQC.
а) C, C1, D, D1, K, M, R (DCC1 )
B,B1, C, C1, P, Q, M (BQC).
D1
К
М
В
R
б) плоскости, в которых лежит
прямая АА1.
С
б) АА1 (АА1D1D);
АА1 (АА1 В1В);
А
D
АА1 (АА1 С1С) и т.д.
в) точки пересечения прямой МК с плоскостью ABD;
прямых DK и ВР с плоскостью А1В1С1
в) МК (АВD) = R
DK (А1В1С1 ) = D1
BP (А1В1С1 ) = Q
5.
Решить задачу: №2В1
Q
С1
P
А1
D1
г) прямые, по которым
пересекаются плоскости
АА1 В1 и АСD;
РВ1 С1 и АВС
г) АА1 В1 АСD = АВ;
РВ1 С1 АВС = ВС
К
М
R
В
А
С
D
д) точки пересечения прямых
МК и DC,
В1 С1 и ВР
С1 М и DC
д) МК DC = R ,
В1 С1 ВР= Q
С1 М DC = C
6.
Решить задачу: №3а) Верно ли, что любые три точки лежат в одной плоскости?
б) Верно ли, что любые четыре точки лежат в одной
D
плоскости?
А
С
В
в) Верно ли, что любые четыре точки не лежат в одной
В1
плоскости?
С1
А1
D1
В
А
D
г) Верно ли, что через любые три точки проходит плоскость,
и притом только одна?
7.
Решить задачу: №5Докажите, что через три данные точки, лежащие на одной
прямой, проходит плоскость. Сколько существует таких
плоскостей?
Дано: А, В, С a
D
А
В
С
a
Доказать:
Доказательство:
Т1
1. D a !
2. Х a ! , , ….
8.
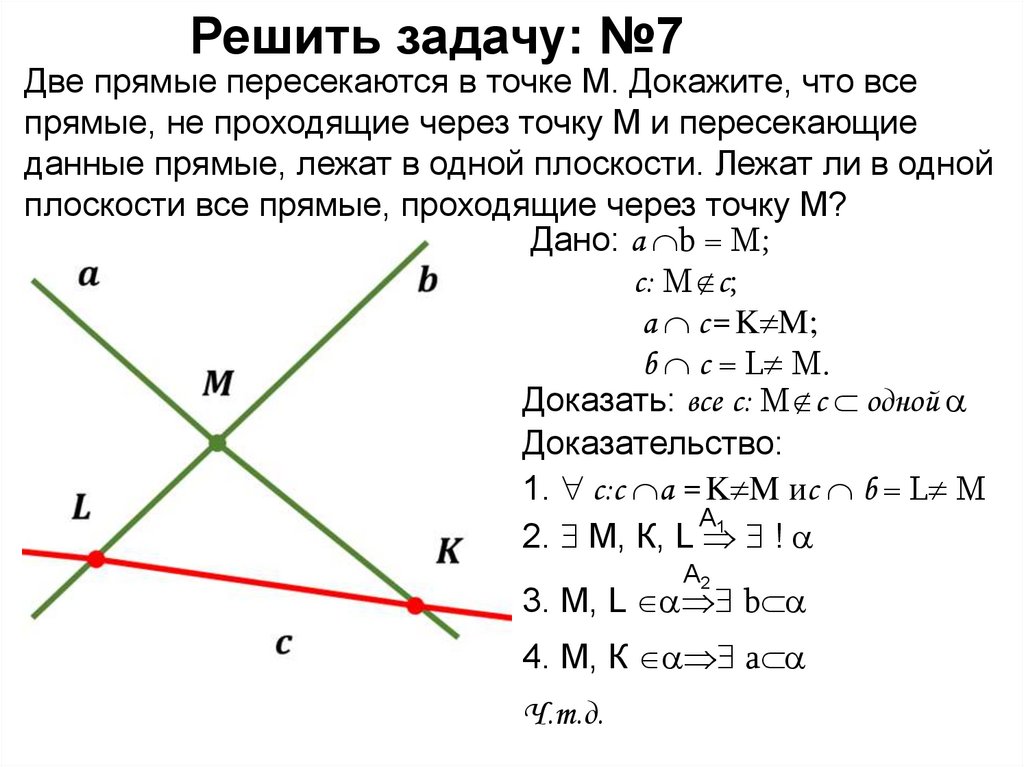
Решить задачу: №7Две прямые пересекаются в точке М. Докажите, что все
прямые, не проходящие через точку М и пересекающие
данные прямые, лежат в одной плоскости. Лежат ли в одной
плоскости все прямые, проходящие через точку М?
Дано: a b = М;
с: М с;
a с= K M;
b c = L M.
Доказать: все с: М с одной
Доказательство:
1. с:с a = K M иc b = L M
А1
2. М, К, L !
А2
3. М, L b
4. М, К a
Ч.т.д.
9.
Решить задачу: №7Две прямые пересекаются в точке М. Докажите, что все
прямые, не проходящие через точку М и пересекающие
данные прямые, лежат в одной плоскости. Лежат ли в одной
плоскости все прямые, проходящие через точку М?
Дано: a b = М;
N с
с: М с.
Доказать: все с: М с одной
a
b
М
Доказательство:
1. N MN
2. a ,b
3. a ,b, c: M a ,b, c
Ч.т.д.
Т2 : Через две пересекающиеся прямые проходит плоскость,
и притом только одна.
10.
Домашнее задание:1. Стр. 3-7 выучить аксиомы и
теоремы с доказательством
2. № 4, 6, 8, 10.









 mathematics
mathematics








