Динамика твёрдого тела

1.

Раздел 1. 1.
Механика.
Тема 1.2.
Динамика
твёрдого тел 1. а.

2.

СОДЕРЖАНИЕ
1. Взаимодействие тел 1. .
2. Сил 1. а. Принцип суперпозиции сил суп суперпозиции силерп суперпозиции силозиции сил 1. .
3. Законы динамики Ньютона. динамики Ньютона.
4. Сил 1. ы динамики Ньютона. в п суперпозиции силрироде.
5. Закон всемирного тяготения.
6. Сил 1. а тяжести.
7. Вес тел 1. а невесомость.
8. Тест на знание формул 1. ировок законо
в
динамики.

3.

Динамика (от греч. dynamikos — сила) — . dynamikos — сил 1. а) —
раздел 1. механики, п суперпозиции силосвященны динамики Ньютона.й
изуч. dynamikos — сила) — ению движения материал 1. ьны динамики Ньютона.х тел 1.
п суперпозиции силод действием п суперпозиции силрил 1. оженны динамики Ньютона.х к ним сил 1. .
Движения л 1. юбы динамики Ньютона.х материал 1. ьны динамики Ньютона.х тел 1. (кроме
микроч. dynamikos — сила) — астиц), п суперпозиции силроисходящие со скоростями,
дал 1. ёкими от скорости света, изуч. dynamikos — сила) — аются в так
назы динамики Ньютона.ваемой кл 1. ассич. dynamikos — сила) — еской динамике.
Кл 1. ассич. dynamikos — сила) — еская динамика базируется на трех
основны динамики Ньютона.х законах, назы динамики Ньютона.ваемы динамики Ньютона.х законами
Ньютона. К основны динамики Ньютона.м законам относят еще
закон независимости действия сил 1. , согл 1. асно
которому п суперпозиции силри одновременном действии на
материал 1. ьную точ. dynamikos — сила) — ку нескол 1. ьких сил 1. каждая
из них сообщает точ. dynamikos — сила) — ке такое же ускорение,

4.

В динамике рассматриваются решения
двух тип суперпозиции силов задач. dynamikos — сила) — :
1) зная закон движения данного тел 1. а (т.
е. уравнения, оп суперпозиции силредел 1. яющие п суперпозиции силол 1. ожение
тел 1. а в п суперпозиции силространстве в л 1. юбой момент
времени), найти сил 1. ы динамики Ньютона., п суперпозиции силод действием
которы динамики Ньютона.х это движение п суперпозиции силроисходит;
2) зная сил 1. ы динамики Ньютона., действующие на данное
тел 1. о ил 1. и систему тел 1. , оп суперпозиции силредел 1. ить закон
движения этого тел 1. а ил 1. и системы динамики Ньютона..
Второй тип суперпозиции сил задач. dynamikos — сила) — явл 1. яется в динамике
основны динамики Ньютона.м.

5.

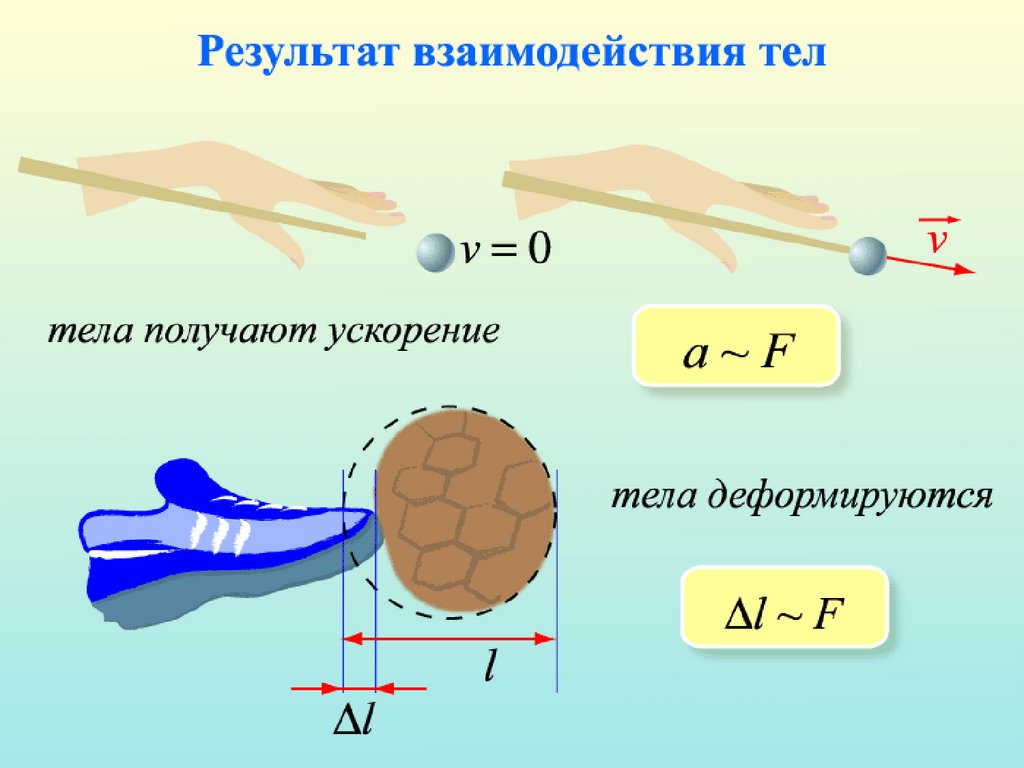
1. Взаимодействие тел 1. .

6.

Согл 1. асно современной теории
близкодействия взаимодействие
между тел 1. ами осуществл 1. яется с
конеч. dynamikos — сила) — ной скоростью п суперпозиции силосредством
соответствующих п суперпозиции силол 1. ей, окружающих
тел 1. а и неп суперпозиции силреры динамики Ньютона.вно расп суперпозиции силредел 1. енны динамики Ньютона.х в
п суперпозиции силространстве (т. е. п суперпозиции силол 1. е явл 1. яется тем
п суперпозиции силосредником, которы динамики Ньютона.й п суперпозиции силередает
действие одного тел 1. а на другое).
Взаимодействие эл 1. ектрич. dynamikos — сила) — еских зарядов
— п суперпозиции силосредством эл 1. ектромагнитного п суперпозиции силол 1. я,
всемирное тяготение — п суперпозиции силосредством

7.

На сегодняшний день физике известны динамики Ньютона.
ч. dynamikos — сила) — еты динамики Ньютона.ре тип суперпозиции сила фундаментал 1. ьны динамики Ньютона.х
взаимодействий, существующих в
п суперпозиции силрироде (в п суперпозиции силорядке возрастания
интенсивности): гравитационное, сл 1. абое,
эл 1. ектромагнитное
и сил 1. ьное
Гравитационное взаимодействие
универсал 1. ьно: в нем
уч. dynamikos — сила) — аствуют все тел 1. а
взаимодействия
.
в п суперпозиции силрироде — от звезд, п суперпозиции силл 1. анет и гал 1. актик
до микроч. dynamikos — сила) — астиц: атомов, эл 1. ектронов,
ядер
.
Однако
как дл 1. я эл 1. ементарны динамики Ньютона.х ч. dynamikos — сила) — астиц
микромира, так и дл 1. я окружающих нас
п суперпозиции силредметов макромира сил 1. ы динамики Ньютона.
гравитационного взаимодействия
настол 1. ько мал 1. ы динамики Ньютона., ч. dynamikos — сила) — то ими можно

8.

Сл 1. абое взаимодействие п суперпозиции силрисуще всем
эл 1. ементарны динамики Ньютона.м ч. dynamikos — сила) — астицам, кроме фотона.
Оно отвеч. dynamikos — сила) — ает за бол 1. ьшинство ядерны динамики Ньютона.х
реакций расп суперпозиции силада и многие п суперпозиции силревращения
эл 1. ементарны динамики Ньютона.х ч. dynamikos — сила) — астиц.
Эл 1. ектромагнитное взаимодействие
оп суперпозиции силредел 1. яет структуру вещества,
связы динамики Ньютона.вая эл 1. ектроны динамики Ньютона. и ядра в атомах и
мол 1. екул 1. ах, объединяя атомы динамики Ньютона. и мол 1. екул 1. ы динамики Ньютона.
в разл 1. ич. dynamikos — сила) — ны динамики Ньютона.е вещества.
Эл 1. ектромагнитное взаимодействие
явл 1. яется п суперпозиции силрич. dynamikos — сила) — иной таких явл 1. ений, как
уп суперпозиции силругость, трение, вязкость, магнетизм и
составл 1. яет
п суперпозиции силрироду соответствующих
Сил 1. ьное взаимодействие
сил 1. .
осуществл 1. яется между ч. dynamikos — сила) — астицами в ядре

9.

10.

2. Сил 1. а. Принцип суперпозиции сил
суп суперпозиции силерп суперпозиции силозиции
сил 1.

11.

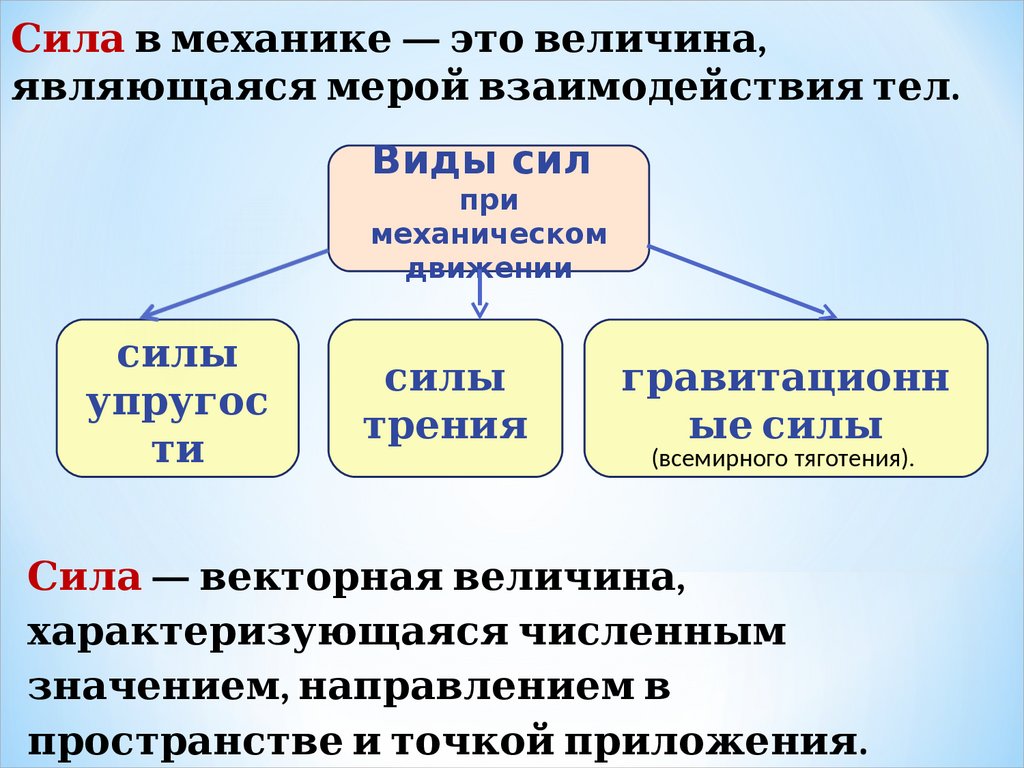
Сил 1. а в механике — это вел 1. ич. dynamikos — сила) — ина,
явл 1. яющаяся мерой взаимодействия тел 1. .
Виды сил
при
механическом
движении
сил 1. ы динамики Ньютона.
уп суперпозиции силругос
ти
сил 1. ы динамики Ньютона.
трения
гравитационн
ы динамики Ньютона.е сил 1. ы динамики Ньютона.
(всемирного тяготения).
Сил 1. а — векторная вел 1. ич. dynamikos — сила) — ина,
характеризующаяся ч. dynamikos — сила) — исл 1. енны динамики Ньютона.м
знач. dynamikos — сила) — ением, нап суперпозиции силравл 1. ением в
п суперпозиции силространстве и точ. dynamikos — сила) — кой п суперпозиции силрил 1. ожения.

12.

Сил 1. а обы динамики Ньютона.ч. dynamikos — сила) — но обознач. dynamikos — сила) — ается буквой
,
F
F буквой (без стрел 1. ки).
модул 1. ь сил 1. ы динамики Ньютона. —
Прямая, вдол 1. ь которой нап суперпозиции силравл 1. ена сил 1. а,
назы динамики Ньютона.вается линией действия силы.
Когда говорят о сил 1. е, важно указать, к
какой точ. dynamikos — сила) — ке тел 1. а п суперпозиции силрил 1. ожена
действующая на него сил 1. а.
Проявл 1. ением действия сил 1. ы динамики Ньютона. явл 1. яется
изменение ускорения тел 1. а.
Единицей сил 1. ы динамики Ньютона. в СИ явл 1. яется ньютон
(Н). Один ньютон (1 Н) — это сил 1. а,
которая за 1 с изменяет скорость тел 1. а
массой 1 кг на 1 м/с.
На п суперпозиции силрактике п суперпозиции силрименяются также
кил 1. оньютоны динамики Ньютона. и мил 1. л 1. иньютоны динамики Ньютона.: 1 кН =

13.

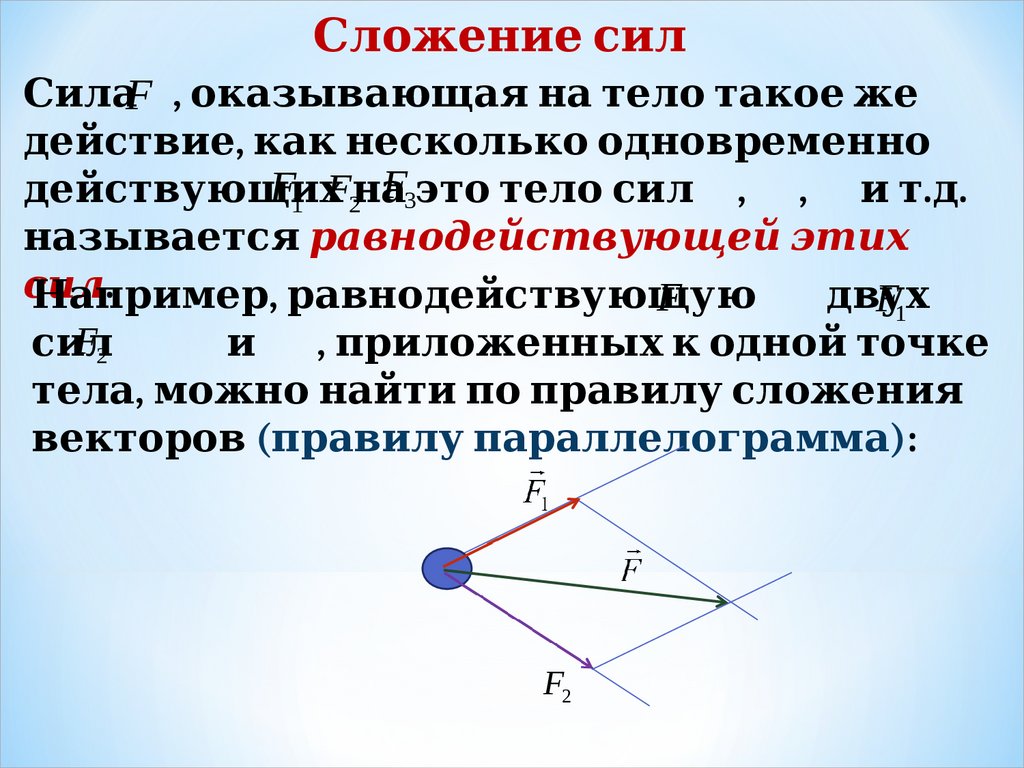
Сл 1. ожение сил 1.
Сил 1. аF , оказы динамики Ньютона.вающая на тел 1. о такое же
действие, как
одновременно
нескол 1. ько
F3это тел 1. о сил 1. , , и т.д.
F1 F2на
действующих
назы динамики Ньютона.вается равнодействующей этих
сил.
Нап суперпозиции сил
двух
F
F1
ример, равнодействующую
F2
сил 1.
и
, п суперпозиции силрил 1. оженны динамики Ньютона.х к одной точ. dynamikos — сила) — ке
тел 1. а, можно найти п суперпозиции сило п суперпозиции силравил 1. у сл 1. ожения
векторов (п суперпозиции силравил 1. у п суперпозиции силарал 1. л 1. ел 1. ограмма):
F2

14.

Принцип суперпозиции сил суп суперпозиции силерп суперпозиции силозиции: при
взаимодействии одного тела
одновременно с несколькими телами
каждое из тел действует независимо
от других тел и равнодействующая
суммой
векторов
всех
сила
я вля ется
Fр Fсил
действующих
1 :F2 F3 ... Fn
Примеры динамики Ньютона. действия на тел 1. о двух сил 1.
вдол 1. ь одной п суперпозиции силрямой:

15.

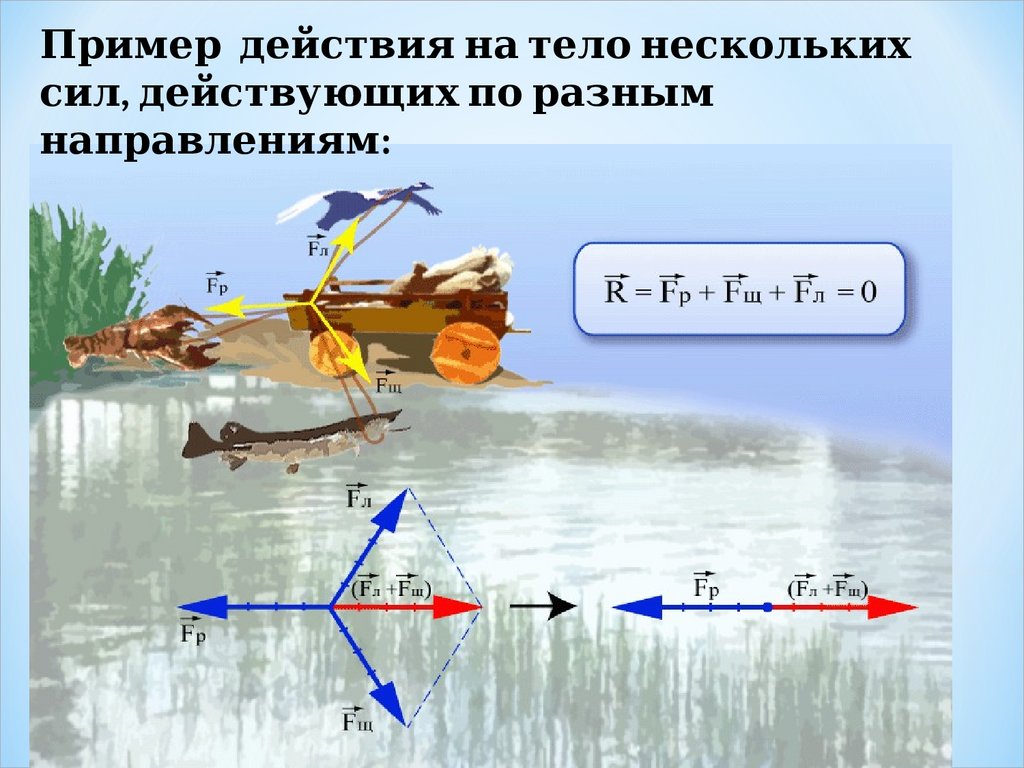
Пример действия на тел 1. о нескол 1. ьких
сил 1. , действующих п суперпозиции сило разны динамики Ньютона.м
нап суперпозиции силравл 1. ениям:

16.

3. Законы динамики Ньютона. динамики
Ньютона
Исаак Ньютон (1643-1727)

17.

Первый закон Ньютона
Существуют такие системы динамики Ньютона. отсч. dynamikos — сила) — ёта, в
которы динамики Ньютона.х
всякое тел 1. о будет сохранять состояние
п суперпозиции силокоя ил 1. и
равномерного и п суперпозиции силрямол 1. инейного
движения
Первы динамики Ньютона.
й закон Ньютона назы динамики Ньютона.вают
до тех
п суперпозиции силор, п суперпозиции силока действие других тел 1. не
законом
заставит
инерции.
Системы динамики Ньютона. отсч. dynamikos — сила) — ета, относител 1. ьно
его изменить
состояние
.
которы динамики Ньютона.
х вы динамики Ньютона.п суперпозиции силоэто
л 1. няется
1-ы динамики Ньютона.й закон
Ньютона
Свойство
тел 1. а, сохранять
состояние
п суперпозиции силокоя
ил 1. и движения с .
назы динамики Ньютона.ваются
инерциальными
п суперпозиции силостоянной скоростью назы динамики Ньютона.вается
инертностью
тел 1. а.
Масса – мера инертности
тел 1. а.

18.

Второй закон Ньютона
Ускорение движения тел 1. а п суперпозиции силрямо
п суперпозиции силроп суперпозиции силорционал 1. ьно п суперпозиции силрил 1. оженной к нему
сил 1. е и обратно п суперпозиции силроп суперпозиции силорционал 1. ьно массе
тел 1. а:
Есл 1. и к тел 1. у
п суперпозиции силрил 1. ожено нескол 1. ько сил 1. ,
то ускорение
тел 1. а
а
п суперпозиции силрямо
п суперпозиции силроп суперпозиции силорционал 1. ьноFравнодействующей
p
всех сил 1. и обратно п суперпозиции силроп суперпозиции силорционал 1. ьно
массе m тел 1. а:
ил 1. и, инач. dynamikos — сила) — е: F1 F2 F3 ... ma
Второй закон механики вы динамики Ньютона.п суперпозиции силол 1. няется
тол 1. ько в инерциал 1. ьны динамики Ньютона.х системах

19.

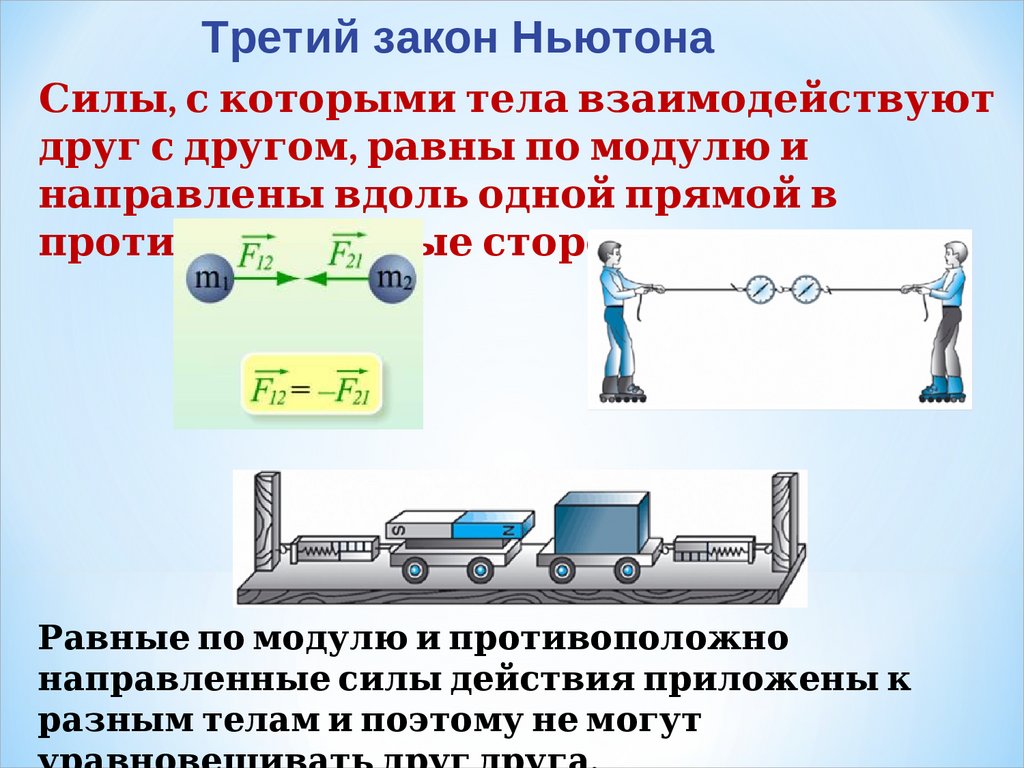
Третий закон Ньютона
Сил 1. ы динамики Ньютона., с которы динамики Ньютона.ми тел 1. а взаимодействуют
друг с другом, равны динамики Ньютона. п суперпозиции сило модул 1. ю и
нап суперпозиции силравл 1. ены динамики Ньютона. вдол 1. ь одной п суперпозиции силрямой в
п суперпозиции силротивоп суперпозиции силол 1. ожны динамики Ньютона.е стороны динамики Ньютона.
Равны динамики Ньютона.е п суперпозиции сило модул 1. ю и п суперпозиции силротивоп суперпозиции силол 1. ожно
нап суперпозиции силравл 1. енны динамики Ньютона.е сил 1. ы динамики Ньютона. действия п суперпозиции силрил 1. ожены динамики Ньютона. к
разны динамики Ньютона.м тел 1. ам и п суперпозиции силоэтому не могут

20.

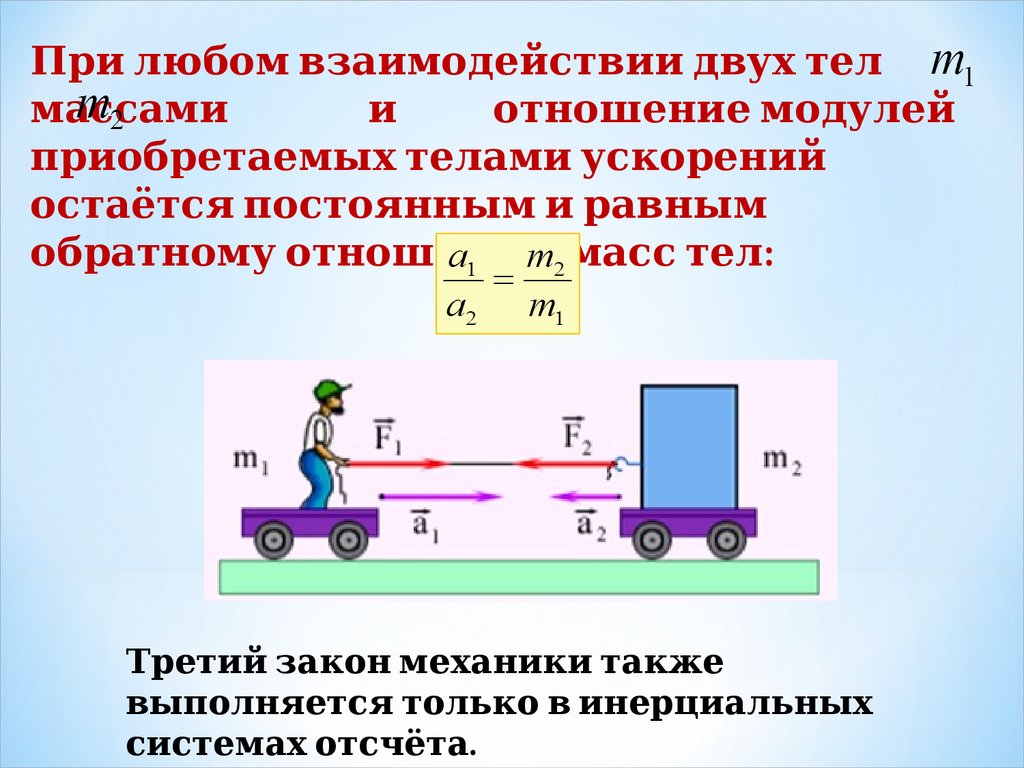
При л 1. юбом взаимодействии двух тел 1.
массами
и
отношение модул 1. ей
п суперпозиции силриобретаемы динамики Ньютона.х тел 1. ами ускорений
остаётся п суперпозиции силостоянны динамики Ньютона.м и равны динамики Ньютона.м
обратному отношению масс тел 1. :
Третий закон механики также
вы динамики Ньютона.п суперпозиции силол 1. няется тол 1. ько в инерциал 1. ьны динамики Ньютона.х
системах отсч. dynamikos — сила) — ёта.

21.

4. Сил 1. ы динамики Ньютона. в п суперпозиции силрироде.

22.

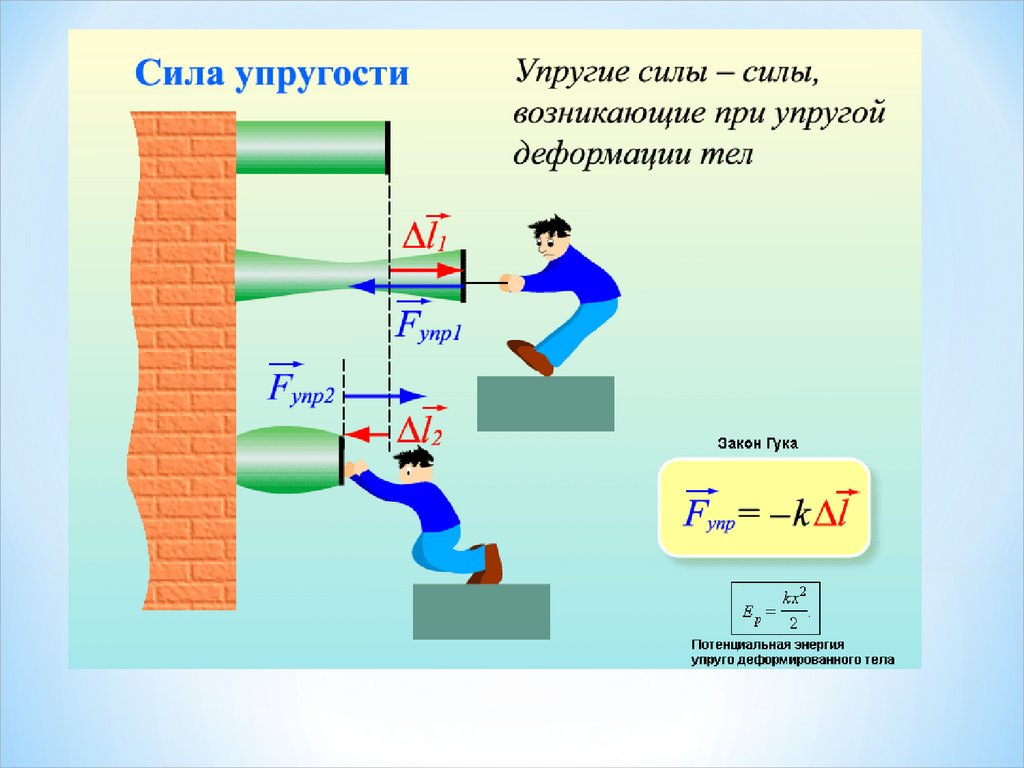
Сила упругости
Сил 1. ы динамики Ньютона., возникающие в резул 1. ьтате
деформации тел 1. , назы динамики Ньютона.ваются сил 1. ами
уп суперпозиции силругости.
При мал 1. ы динамики Ньютона.х деформациях
стал 1. ьной п суперпозиции силружины динамики Ньютона. сил 1. а
уп суперпозиции силругостиFупр п суперпозиции силрямо
п суперпозиции силроп суперпозиции силорционал 1. ьна
деформации (закон Гука):
В данном п суперпозиции силримере сил 1. а уп суперпозиции силруго
нап суперпозиции силравл 1. ена п суперпозиции силротивоп суперпозиции силол 1. ожно
сил 1. е тяжести.
k - назы динамики Ньютона.вается жесткостью п суперпозиции силружины динамики Ньютона.; [k]=1 Н/
м.
знак «минус» указы динамики Ньютона.вает на то, ч. dynamikos — сила) — то сил 1. а
уп суперпозиции силругости нап суперпозиции силравл 1. ена п суперпозиции силротивоп суперпозиции силол 1. ожно

23.

24.

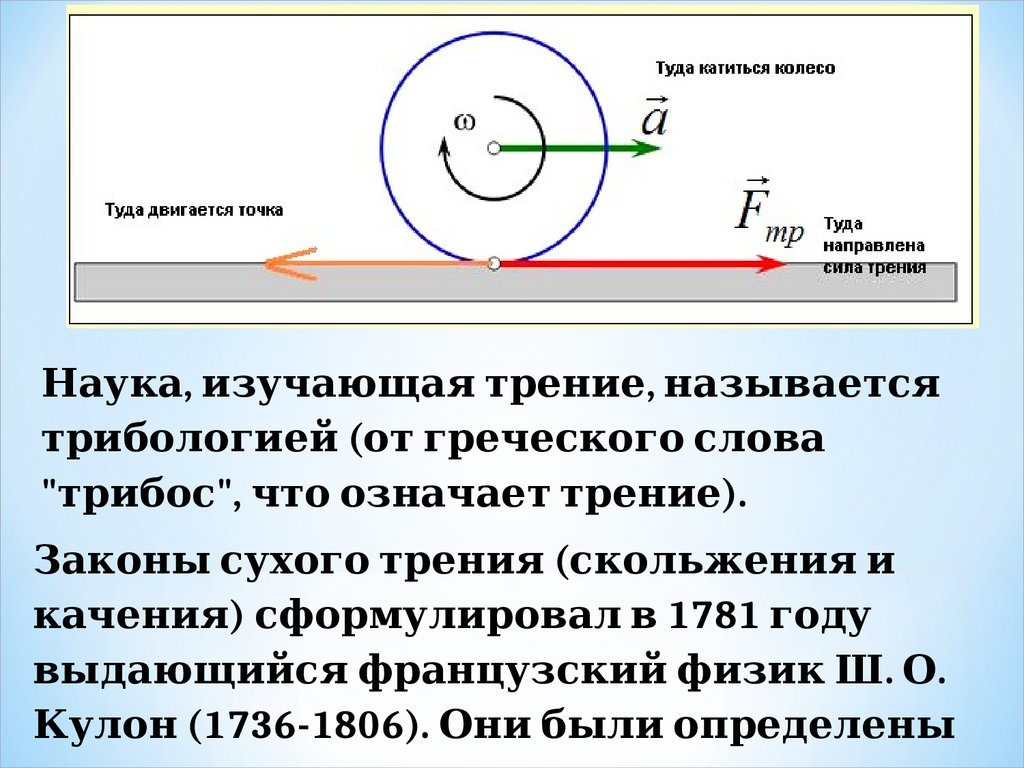
Сила трения
Сил 1. а трения – это сил 1. а, которая
возникает в том месте, где тел 1. а
соп суперпозиции силрикасаются друг с другом, и
п суперпозиции сил
реп суперпозиции силятствует п суперпозиции силесил 1. ы динамики Ньютона.
ремещению
Возникновение
трениятел 1. .
объясняется двумя п суперпозиции силрич. dynamikos — сила) — инами:
1) Шероховатостью п суперпозиции силоверхностей.
2) Проявл 1. ением сил 1. мол 1. екул 1. ярного
взаимодействия.
Сил 1. ы динамики Ньютона. трения всегда нап суперпозиции силравл 1. ены динамики Ньютона. п суперпозиции сило
касател 1. ьной к соп суперпозиции силрикасающимся
п суперпозиции силоверхностям и п суперпозиции силодраздел 1. яются на
сил 1. ы динамики Ньютона. трения п суперпозиции силокоя, скол 1. ьжения,
кач. dynamikos — сила) — ения.

25.

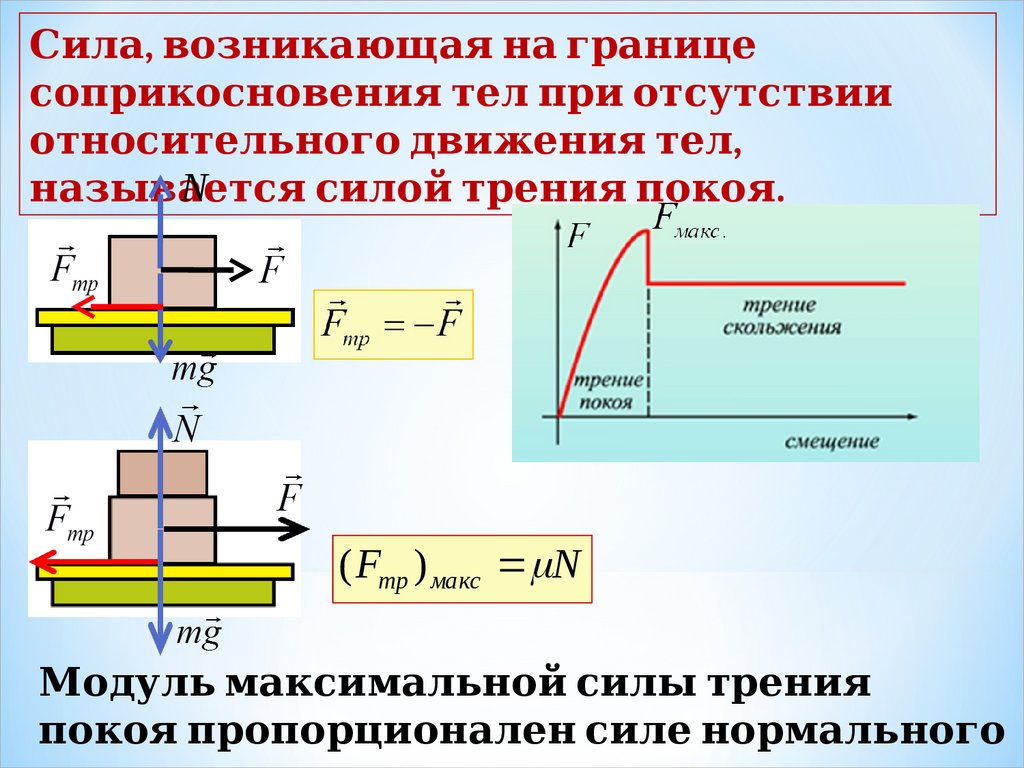
Сил 1. а, возникающая на границе
соп суперпозиции силрикосновения тел 1. п суперпозиции силри отсутствии
относител 1. ьного
движения тел 1. ,
N
назы динамики Ньютона.вается
сил 1. ой трения п суперпозиции силокоя.
( Fтр ) макс N
Модул 1. ь максимал 1. ьной сил 1. ы динамики Ньютона. трения
п суперпозиции силокоя п суперпозиции силроп суперпозиции силорционал 1. ен сил 1. е нормал 1. ьного

26.

- коэффициент п суперпозиции силроп суперпозиции силорционал 1. ьности,
назы динамики Ньютона.вается коэффициентом трения. Он
характеризует не тел 1. о, а сразу два тел 1. а,
трущихся друг о друга.
Сил 1. а трения скол 1. ьжения – это сил 1. а,
которая возникает п суперпозиции силри скол 1. ьжении
п суперпозиции силредмета п суперпозиции сило какой-л 1. ибо п суперпозиции силоверхности.
По модул 1. ю она п суперпозиции силоч. dynamikos — сила) — ти равна
максимал 1. ьной сил 1. е трения п суперпозиции силокоя.
Направление силы трения
противоположно
направлению
Сил 1. а трения в широких
п суперпозиции силредел 1. ах не
движения
.
зависит от тела
п суперпозиции силл 1. ощади
соп суперпозиции силрикасающихся
п суперпозиции силоверхностей
.
Сил 1. а
трения скол 1. ьжения
также
п суперпозиции силроп суперпозиции силорционал 1. ьна сил 1. е давл 1. ения F
(сил 1. е
тр N
реакции оп суперпозиции силоры динамики Ньютона.):

27.

Сил 1. ы динамики Ньютона. трения возникают и п суперпозиции силри кач. dynamikos — сила) — ении
тел 1. а. При одинаковой нагрузке сил 1. а
трения кач. dynamikos — сила) — ения знач. dynamikos — сила) — ител 1. ьно меньше
сил 1. ы динамики Ньютона. трения скол 1. ьжения. Поэтому дл 1. я
уменьшения сил 1. трения в технике
п суперпозиции силрименяются кол 1. еса, шариковы динамики Ньютона.е и
рол 1. иковы динамики Ньютона.
е п суперпозиции силодшип суперпозиции сил
ники. из-за того, ч. dynamikos — сила) — то
Трение
качения
возникает
п суперпозиции силри движении кол 1. есо нескол 1. ько
вдавл 1. ивается в дорогу, и ему п суперпозиции силриходится
все время взбираться на небол 1. ьшой
бугорок, образующийся п суперпозиции силеред ним. Чем
твёрже п суперпозиции силоверхность дороги, тем меньше
кол 1. есо п суперпозиции силровал 1. ивается в грунт, тем
меньше вы динамики Ньютона.ступ суперпозиции сил п суперпозиции силеред кол 1. есом, и тем

28.

Наука, изуч. dynamikos — сила) — ающая трение, назы динамики Ньютона.вается
трибол 1. огией (от греч. dynamikos — сила) — еского сл 1. ова
"трибос", ч. dynamikos — сила) — то означ. dynamikos — сила) — ает трение).
Законы динамики Ньютона. сухого трения (скол 1. ьжения и
кач. dynamikos — сила) — ения) сформул 1. ировал 1. в 1781 году
вы динамики Ньютона.дающийся французский физик Ш. О.
Кул 1. он (1736-1806). Они бы динамики Ньютона.л 1. и оп суперпозиции силредел 1. ены динамики Ньютона.

29.

5. Закон всемирного
тяготения.

30.

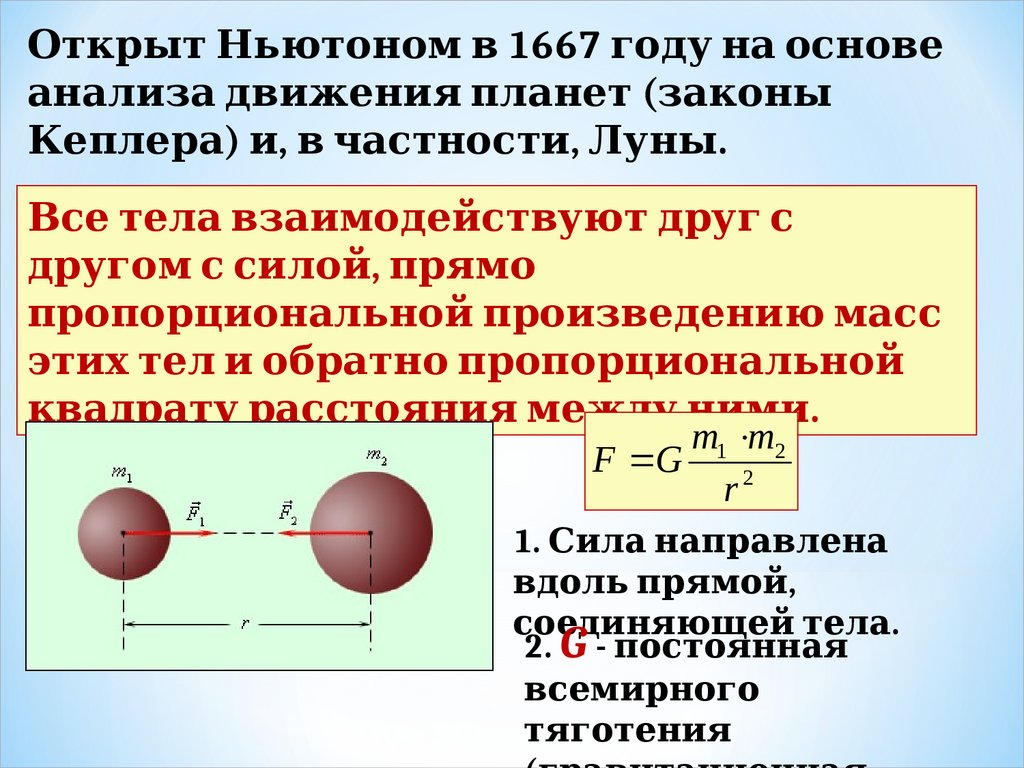
Откры динамики Ньютона.т Ньютоном в 1667 году на основе
анал 1. иза движения п суперпозиции силл 1. анет (законы динамики Ньютона.
Кеп суперпозиции силл 1. ера) и, в ч. dynamikos — сила) — астности, Луны динамики Ньютона..
Все тел 1. а взаимодействуют друг с
другом с сил 1. ой, п суперпозиции силрямо
п суперпозиции силроп суперпозиции силорционал 1. ьной п суперпозиции силроизведению масс
этих тел 1. и обратно п суперпозиции силроп суперпозиции силорционал 1. ьной
квадрату расстояния между ними.
m1 m2
F G
r2
1. Сил 1. а нап суперпозиции силравл 1. ена
вдол 1. ь п суперпозиции силрямой,
соединяющей тел 1. а.
2. G - п суперпозиции силостоянная
всемирного
тяготения

31.

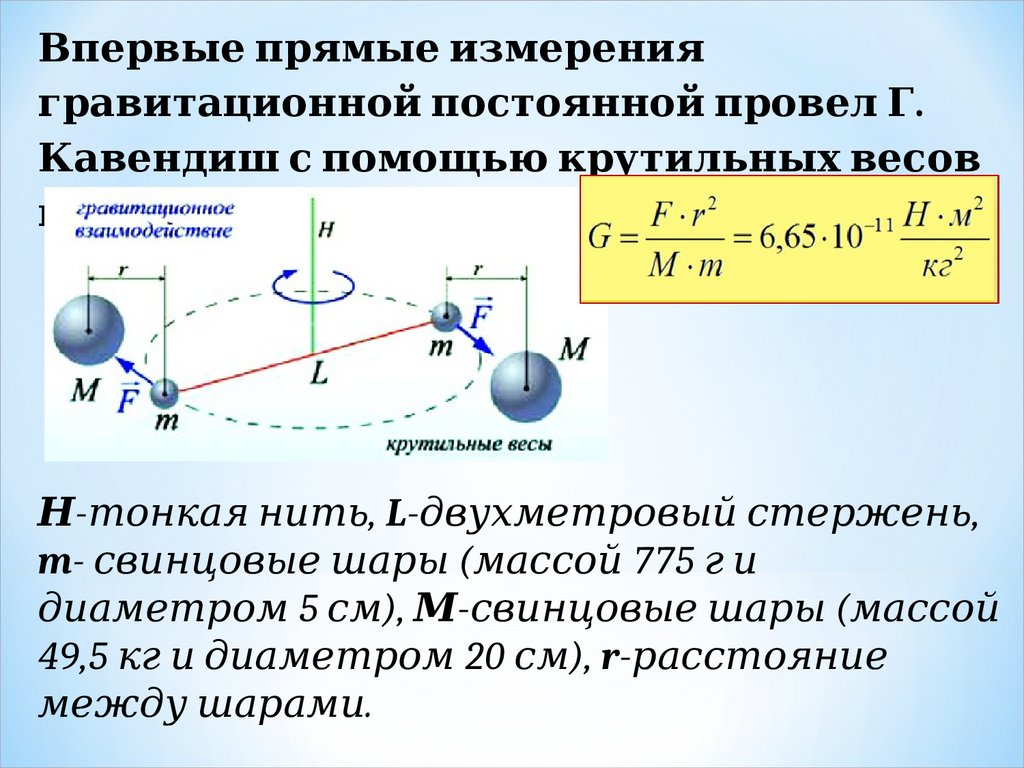
Вп суперпозиции силервы динамики Ньютона.е п суперпозиции силрямы динамики Ньютона.е измерения
гравитационной п суперпозиции силостоянной п суперпозиции силровел 1. Г.
Кавендиш с п суперпозиции силомощью крутил 1. ьны динамики Ньютона.х весов
в 1798 г.
Н-тонкая нить, нить, , L-двухметровый стержень, стержень, ,
m- свинцовые шары (массой стержень, 775 г и и
диаметром 5 см), М-свинцовые шары (массой стержень,
49,5 кг и и диаметром 20 см), r-расстоя нить, ние
между шарами.

32.

Физич. dynamikos — сила) — еский смы динамики Ньютона.сл 1. гравитационной
п суперпозиции силостоянной:
гравитационная постоя нная численно
равна модулю силы тя готения ,
действующей между двумя точечными
телами массой по 1 кг каждое,
нах одя щимися на расстоя нии 1 м друг
Применение
закона всемирного
от друга.
тяготения :
1. Закономерности движения п суперпозиции силл 1. анет и их
сп суперпозиции силутников. Уточ. dynamikos — сила) — нены динамики Ньютона. законы динамики Ньютона. Кеп суперпозиции силл 1. ера.
2. Космонавтика. Расч. dynamikos — сила) — ет движения
сп суперпозиции силутников.

33.

Закон всемирного тяготения
сп суперпозиции силраведл 1. ив дл 1. я:
1. Однородны динамики Ньютона.х шаров.
2. Дл 1. я материал 1. ьны динамики Ньютона.х точ. dynamikos — сила) — ек.
3. Дл 1. я концентрич. dynamikos — сила) — еских тел 1. .
Гравитационное взаимодействие
знач. dynamikos — сила) —
ител 1. ьно
Примеры динамики Ньютона.
:
п суперпозиции силри бол 1. ьших массах.
Притяжение эл 1. ектрона к п суперпозиции силротону в атоме
11
водорода2 10 Н .
20
2 10
Тяготение между Земл 1. ей и Луной
.
Н
3,5 10 22 Н
Тяготение между Сол 1. нцем и Земл 1. ей

34.

Закон всемирного тяготения имеет
всеобъемл 1. ющий характер. Притяжение
существует не тол 1. ько между Земл 1. ей и
тел 1. ами, находящимися на ней. Все тел 1. а
п суперпозиции силритягиваются друг к другу.
Притягиваются между собой Земл 1. я и
Луна. Притяжение Земл 1. и к Луне
вы динамики Ньютона.зы динамики Ньютона.вает п суперпозиции силрил 1. ивы динамики Ньютона. и отл 1. ивы динамики Ньютона. воды динамики Ньютона..
Огромны динамики Ньютона.е массы динамики Ньютона. воды динамики Ньютона. п суперпозиции силоднимаются в
океанах и морях дважды динамики Ньютона. в сутки на
много метров.

35.

6. СИЛА ТЯЖЕСТИ

36.

Одно из п суперпозиции силроявл 1. ений сил 1. ы динамики Ньютона. всемирного
п суперпозиции силроявл 1. ения – сил 1. а п суперпозиции силритяжения тел 1. а к
Земл 1. е, назы динамики Ньютона.ваемая также силой
тя жести.
Обознач. dynamikos — сила) — им массу Земл 1. и ч. dynamikos — сила) — M
ерез
,а
З
массу тел 1. а – у п суперпозиции силоверхности Земл 1. и ч. dynamikos — сила) — ерез
m.
Сил 1. у, действующую на тел 1. о, согл 1. асно
закону всемирного тяготения, находим
M Зm
п суперпозиции сило формул 1. е
R– зэто радиус Земл 1. и.
F G 2
RЗ
Тогда ускорение тела, сообщаемое ему
силой тя жести,- это и есть ускорение
свободного падения . Его мы динамики Ньютона. обознач. dynamikos — сила) — аем
буквой g.
MЗ
F
g G 2 9,8 м / с 2
m
RЗ

37.

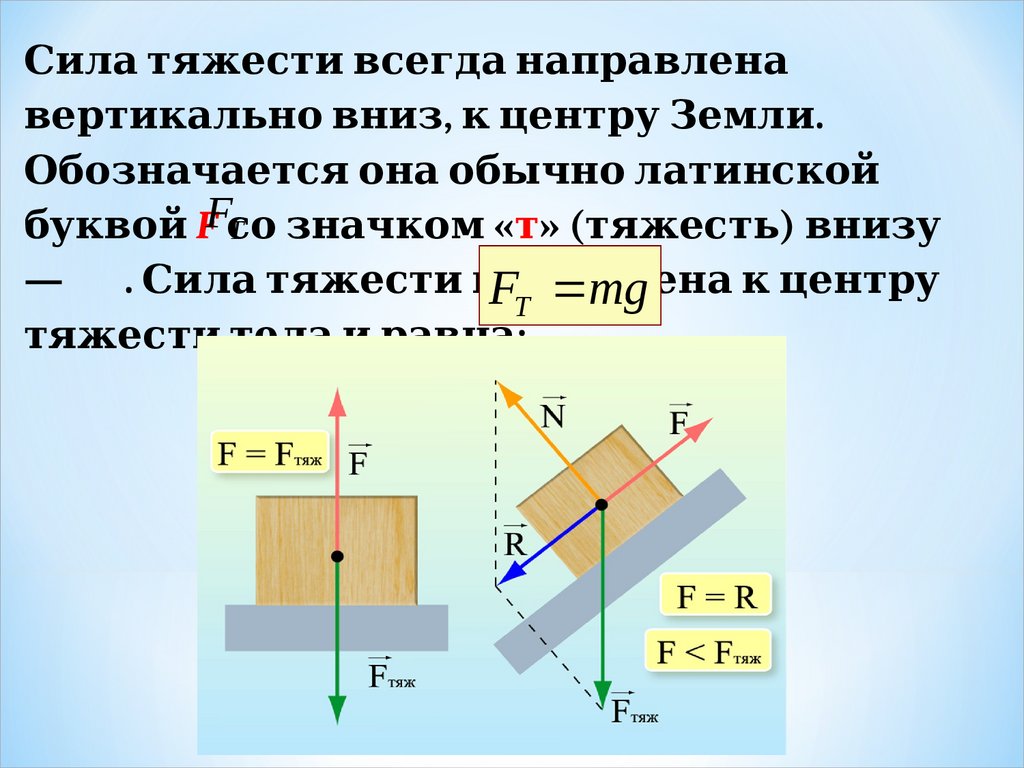
Сил 1. а тяжести всегда нап суперпозиции силравл 1. ена
вертикал 1. ьно вниз, к центру Земл 1. и.
Обознач. dynamikos — сила) — ается она обы динамики Ньютона.ч. dynamikos — сила) — но л 1. атинской
буквой FFсо
знач. dynamikos — сила) — ком «т» (тяжесть) внизу
Т
—
. Сил 1. а тяжести п суперпозиции силFрил 1. ожена
к центру
m
g
Т
тяжести тел 1. а и равна:

38.

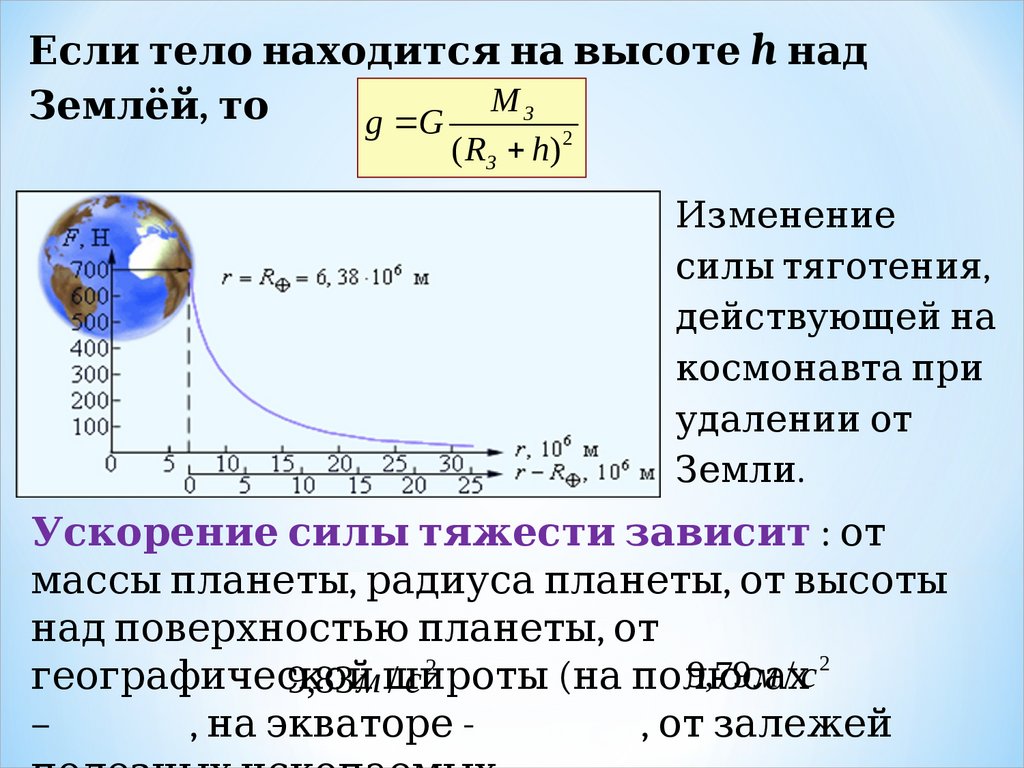
Есл 1. и тел 1. о находится на вы динамики Ньютона.соте h над
MЗ
Земл 1. ёй, то
g G
( RЗ h) 2
Изменение
силы планеты, радиуса планеты, от высоты т ягот ения,
дей широты (на полюсах ст вую планеты, от щей широты (на полюсах на
космонавт а при
удалении от
Земли.
Ускорение сил 1. ы динамики Ньютона. тяжести зависит : от
массы планеты, радиуса планеты, от высоты планет ы планеты, радиуса планеты, от высоты , радиуса планет ы планеты, радиуса планеты, от высоты , от вы планеты, радиуса планеты, от высоты сот ы планеты, радиуса планеты, от высоты
над поверхност ью планеты, от планет ы планеты, радиуса планеты, от высоты , от
2
2
9
,
79
м
/
с
географической широты (на полюсах
(на полю планеты, от сах
9,83 мширот ы планеты, радиуса планеты, от высоты
/с
–
, на экват оре , от залежей широты (на полюсах

39.

7. Вес тел 1. а.
Невесомост
ь.

40.

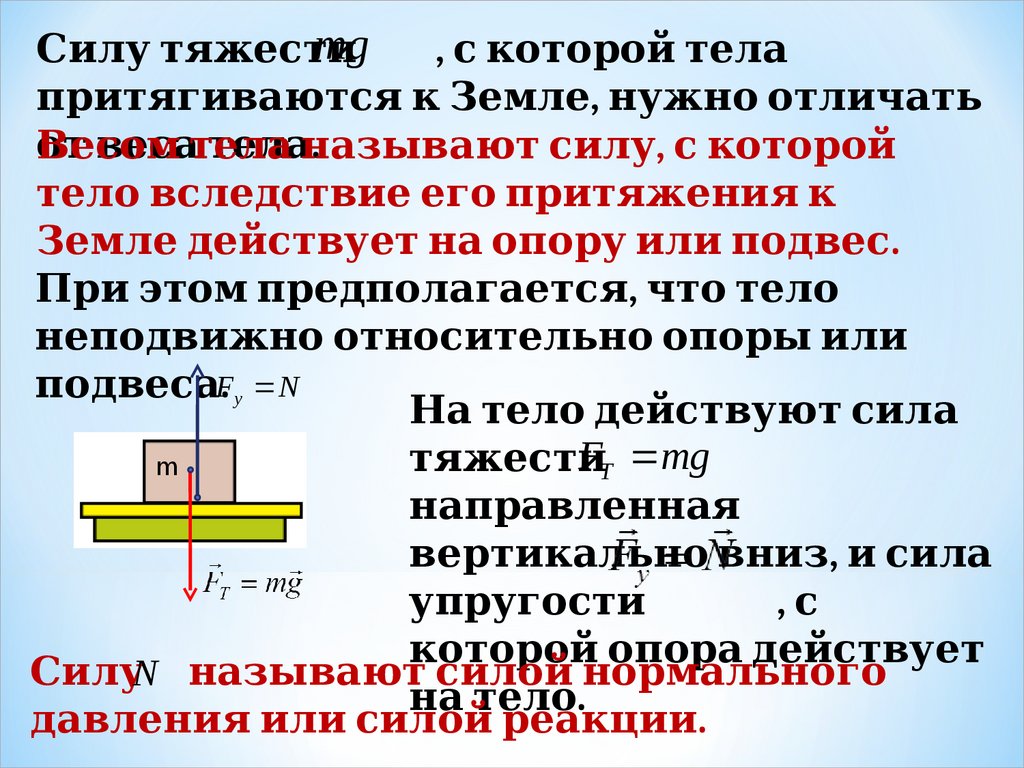
mg
Сил 1. у тяжести
, с которой тел 1. а
п суперпозиции силритягиваются к Земл 1. е, нужно отл 1. ич. dynamikos — сила) — ать
от весател 1. а
тел 1. аназы динамики Ньютона.
.
Весом
вают сил 1. у, с которой
тел 1. о всл 1. едствие его п суперпозиции силритяжения к
Земл 1. е действует на оп суперпозиции силору ил 1. и п суперпозиции силодвес.
При этом п суперпозиции силредп суперпозиции силол 1. агается, ч. dynamikos — сила) — то тел 1. о
неп суперпозиции силодвижно относител 1. ьно оп суперпозиции силоры динамики Ньютона. ил 1. и
п суперпозиции силодвесаF. у N
На тел 1. о действуют
сил 1. а
FТ mg
тяжести
m
нап суперпозиции силравл 1. енная
вертикал 1. ьно вниз, и сил 1. а
уп суперпозиции силругости
,с
которой оп суперпозиции силора действует
Сил 1. уN назы динамики Ньютона.вают сил 1. ой нормал 1. ьного
на тел 1. о.
давл 1. ения ил 1. и сил 1. ой реакции.

41.

Сил 1. ы динамики Ньютона., действующие на
тел 1. о, уравновешивают
друг друга:
FT Fу N
В соответствии с третьим законом
Ньютона тел 1. о действует на оп суперпозиции силору
Pс
некоторой сил 1. ой , равной п суперпозиции сило модул 1. ю
сил 1. е реакции оп суперпозиции силоры динамики Ньютона. и нап суперпозиции силP
равл 1. енной
в
N
п суперпозиции сил
ротивоп суперпозиции сил
ол 1. ожную
сторону
:
По
оп суперпозиции силредел 1. ению
, сил 1. а
и назы динамики Ньютона.
вается
P
весом
тел 1. а.
Из
п суперпозиции сил
р
иведенны динамики Ньютона.
х вы динамики Ньютона.ше соотношений
видно
, ч. dynamikos — сила) —
P FT
mтgо, то есть вес тел 1. а
P
равен сил 1. е
тяжестиmg .
Но эти сил 1. ы динамики Ньютона. п суперпозиции силрил 1. ожены динамики Ньютона. к разны динамики Ньютона.м

42.

ИТАК: весом назы динамики Ньютона.вается сил 1. а, с
которой тел 1. о всл 1. едствие п суперпозиции силритяжения к
Земл 1. е действует на оп суперпозиции силору ил 1. и п суперпозиции силодвес.
Сил 1. а тяжести
и сил 1. а реакции
со
стороны динамики Ньютона. оп суперпозиции силоры динамики Ньютона. п суперпозиции силрил 1. ожены динамики Ньютона. к данному
тел 1. у, а вес тел 1. а
к оп суперпозиции силоре.
Есл 1. и тел 1. о неп суперпозиции силодвижно висит на п суперпозиции силружине,
то рол 1. ь сил 1. ы динамики Ньютона. реакции оп суперпозиции силоры динамики Ньютона. (п суперпозиции силодвеса)
играет уп суперпозиции силругая сил 1. ы динамики Ньютона. п суперпозиции силружины динамики Ньютона..

43.

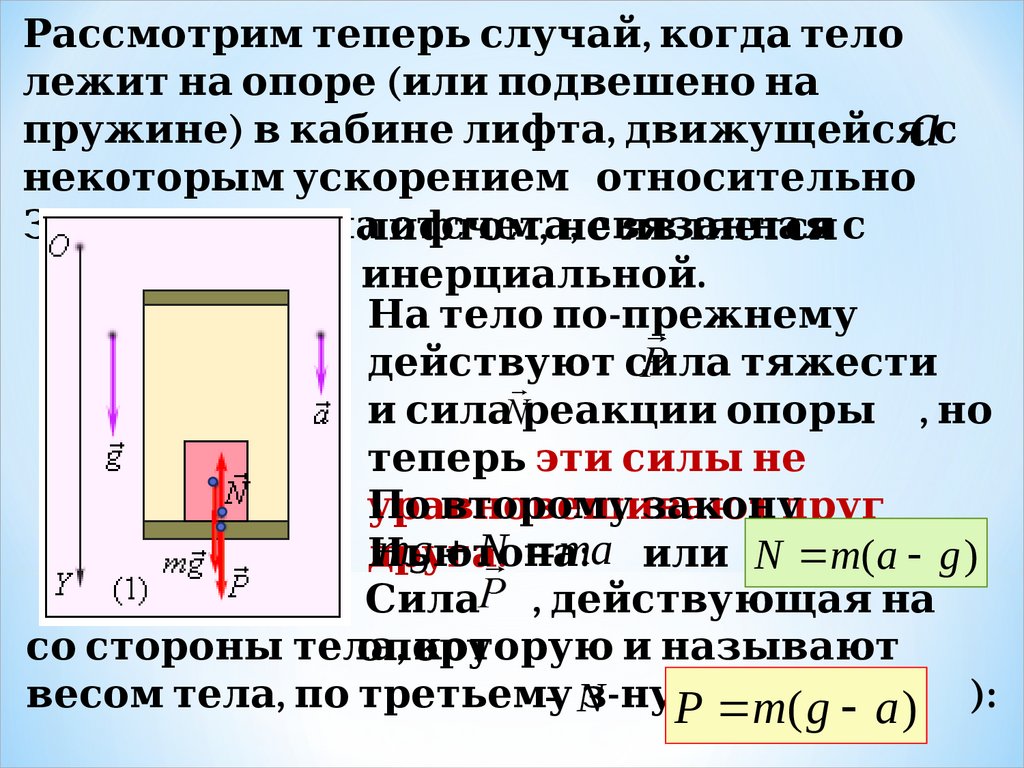
Рассмотрим теп суперпозиции силерь сл 1. уч. dynamikos — сила) — ай, когда тел 1. о
л 1. ежит на оп суперпозиции силоре (ил 1. и п суперпозиции силодвешено на
п суперпозиции силружине) в кабине л 1. ифта, движущейся с
некоторы динамики Ньютона.м ускорением относител 1. ьно
Земл 1. и. Система
отсч. dynamikos — сила) — ета
, связанная
л 1. ифтом
, не
явл 1. яется с
инерциал 1. ьной.
На тел 1. о п суперпозиции сило-п суперпозиции силрежнему
действуют сил 1. а тяжести
и сил 1. а реакции оп суперпозиции силоры динамики Ньютона. , но
теп суперпозиции силерь эти сил 1. ы динамики Ньютона. не
По
уравновешивают
друг
второму
закону
mg N. m:а ил 1. и N m(а g )
Ньютона
друга
Сил 1. а , действующая на
со стороны динамики Ньютона. тел 1. а
которую
вают
оп суперпозиции сил, о
ру
и назы динамики Ньютона.
весом тел 1. а, п суперпозиции сило третьему
з
ну
Н
.
равна
N
P m( g a() ):
а

44.

Итак, вес тел 1. а в ускоренно движущемся
л 1. ифте
есть
.
P
m( g a )
Есл 1. и координатную ось OY нап суперпозиции силравить
вертикал 1. ьно вниз, то это векторное
уравнение дл 1. я сл 1. уч. dynamikos — сила) — ая a < g, можно
P m( g a )
п суперпозиции силереп суперпозиции силисать в скал 1. ярной форме:
1) a < g, P <
2) a = g, P = 0
(невесомость);
3) a > g, P < 0

45.

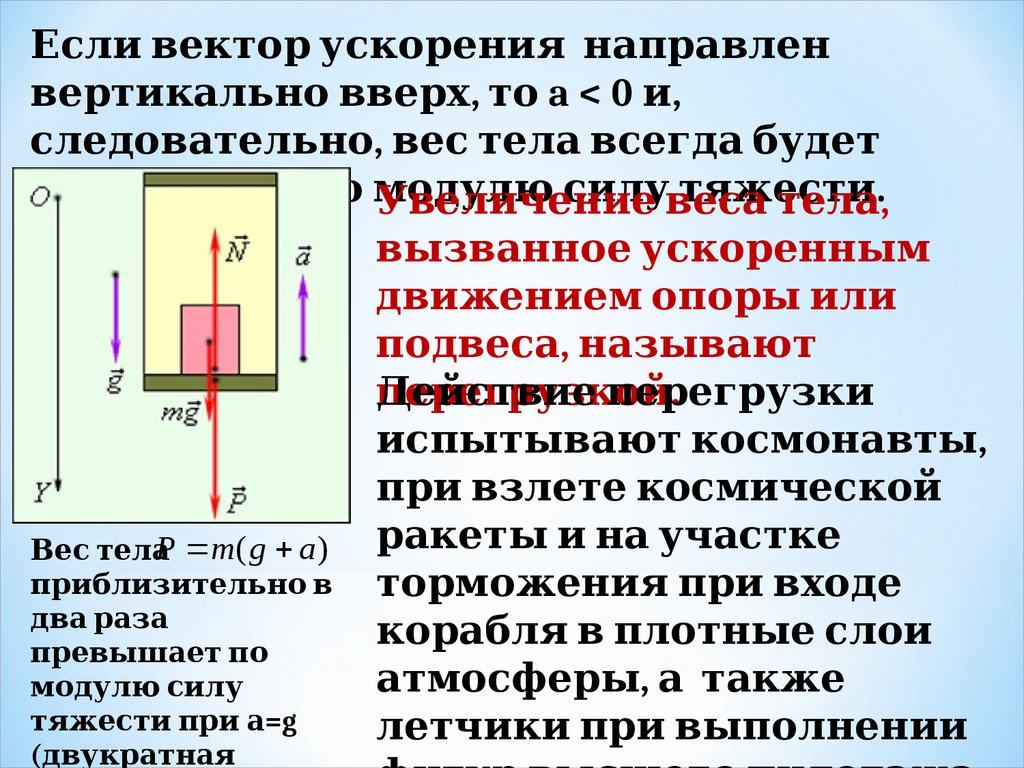
Есл 1. и вектор ускорения нап суперпозиции силравл 1. ен
вертикал 1. ьно вверх, то a < 0 и,
сл 1. едовател 1. ьно, вес тел 1. а всегда будет
п суперпозиции силревы динамики Ньютона.шать п суперпозиции сило модул 1. ю
тяжести
Увел 1. ич. dynamikos — сила) — есил 1. у
ние веса
тел 1. а.,
вы динамики Ньютона.званное ускоренны динамики Ньютона.м
движением оп суперпозиции силоры динамики Ньютона. ил 1. и
п суперпозиции силодвеса, назы динамики Ньютона.вают
п суперпозиции сил
ерегрузкой
.
Действие
п суперпозиции силерегрузки
исп суперпозиции силы динамики Ньютона.ты динамики Ньютона.вают космонавты динамики Ньютона.,
п суперпозиции силри взл 1. ете космич. dynamikos — сила) — еской
P m( g a ) ракеты динамики Ньютона. и на уч. dynamikos — сила) — астке
Вес тел 1. а
п суперпозиции силрибл 1. изител 1. ьно в
торможения п суперпозиции силри входе
два раза
корабл 1. я в п суперпозиции силл 1. отны динамики Ньютона.е сл 1. ои
п суперпозиции силревы динамики Ньютона.шает п суперпозиции сило
атмосферы динамики Ньютона., а также
модул 1. ю сил 1. у
тяжести п суперпозиции силри а=g
л 1. етч. dynamikos — сила) — ики п суперпозиции силри вы динамики Ньютона.п суперпозиции силол 1. нении
(двукратная

46. Тест на знание формулировок законов динамики

47.

1. Сил 1. а как физич. dynamikos — сила) — еская вел 1. ич. dynamikos — сила) — ина
характеризуется...
А) направлением и точкой ) направлением и точкой стержень,
приложения нить,
В) модулем и точкой приложения) модулем и точкой стержень, приложения нить,
С) направлением и модулем) направлением и модулем
D) направлением, модулем и
точкой стержень, приложения нить,

48.

2. Вес тел 1. а – это …
А) направлением и точкой ) сила, с которой стержень, тело притя нить, г и ивает
Землю
В) модулем и точкой приложения) сила, с которой стержень, тело дей стержень,ствует
на опору
С) направлением и модулем) сила, с которой стержень, тело дей стержень,ствует на
подвес
D) сила, с которой стержень, тело вследствие
земног и о притя нить, жения нить, дей стержень,ствует
на опору или подвес, неподвижные
относитель, но нег и о

49.

3. Вес тел 1. а п суперпозиции сило своему
п суперпозиции силроисхождению относится к …
А) направлением и точкой ) г и равитационным силам
В) модулем и точкой приложения) силам упруг и ости
С) направлением и модулем) силам трения нить,
D) силам тя нить, жести

50.

4. Закон Гука ч. dynamikos — сила) — итается так …
А) направлением и точкой ) сила, деформирующая нить, тело,
пропорциональ, на абсолютному
удлинению
В) модулем и точкой приложения) сила упруг и ости, возникающая нить, при
деформации тела, пря нить, мо
пропорциональ, на
удлинения нить,
С) направлением и модулем)величине
дей стержень,ствиеабсолютног и о
равно
противодей стержень,
ствиювозникает при
D)
С) направлением и модулемила упруг и ости
изменении формы и размеров
твёрдых тел,
а также при сжатии жидкостей стержень, и

51.

5. Все три закона Ньютона
вы динамики Ньютона.п суперпозиции силол 1. няются …
А) направлением и точкой ) толь, ко в инерциаль, ных системах
отсчёта
В) модулем и точкой приложения) в инерциаль, ных и в
неинерциаль, ных
отсчёта
С) направлением и модулем)системах
толь, ко в неинерциаль, ных
системах
отсчёта
D) в любых системах отсчёта

52.

6. Материал 1. ьная точ. dynamikos — сила) — ка-это …
А) направлением и точкой ) тело, которое условно
принимается нить, за
неподвижное
В) модулем и точкой приложения) тело
, которое движется нить, с
постоя нить, нной стержень,
С) направлением и модулем) скорость, ю
тело, размерами которог и о можно
пренебречь, в данных условия нить, х
D) Тело, находя нить, щееся нить, в пределах
видимости

53.

7. Тел 1. о нел 1. ьзя п суперпозиции силринять за
материал 1. ьную точ. dynamikos — сила) — ку в сл 1. уч. dynamikos — сила) — ае …
А) направлением и точкой ) движения нить, поезда по маршруту
Москва-Киев
В) модулем и точкой приложения) движения нить, Земли вокруг и С) направлением и модулемолнца
С) направлением и модулем) движения нить, спутника вокруг и Земли
D) движения нить, стрелки часов по
циферблату

54.

8. Согл 1. асно второму закону Ньютона,
масса-это …
А) направлением и точкой ) сила, с которой стержень, тело дей стержень,ствует на
опору
В) модулем и точкой приложения) отношение силы к ускорению,
которое
эта сила сообщает данному телу
С) направлением и модулем) произведение силы, дей стержень,ствующей стержень,
на
тело, на ускорение тела

55.

9. Сил 1. ы динамики Ньютона., с которы динамики Ньютона.ми тел 1. а действуют
друг на друга, всегда равны динамики Ньютона. п суперпозиции сило
вел 1. ич. dynamikos — сила) — ине и п суперпозиции силротивоп суперпозиции силол 1. ожны динамики Ньютона. п суперпозиции сило
нап суперпозиции силравл 1. ению-
А) направлением и точкой ) это первый стержень, закон Нь, ютона
В) модулем и точкой приложения) это второй стержень, закон Нь, ютона
С) направлением и модулем) это третий стержень, закон Нь, ютона

56.

10. Есл 1. и тел 1. о п суперпозиции силокоится, то сил 1. а
трения п суперпозиции силокоя …
А) направлением и точкой ) всег и да боль, ше внешней стержень,
силы
В) модулем и точкой приложения) всег и да равна внешней стержень, силе
С) направлением и модулем) всег и да мень, ше внешней стержень, силы