Similar presentations:
Уравнение решение задач
1.
2.
х х0 у - у0 z z02
2
2
2
х - х 0 у - у0 z z0 r
d
2
2
2
3. Упражнение 1. В данных уравнениях определите координаты центра сферы и радиус
• 1.( х 2) ( у 4) z 7 9
• 2.
( х 6) ( у 0,5) z 5
• 3.
х у ( z 1) 6
• 4.
х у z 49
2
2
2
2
2
2
2
2
2
2
2
2
4.
Упражнение 2.Составьте уравнение сферы по следующим
данным центра и радиуса сферы:
1.Дано: С(-2;8;1);
R=11
2.Дано: А(3;-2;0);
R=0,7
3.Дано: О(0;0;0);
R=1
Проверяем ответы:
х 2 у 8 z 1 121
2
2
2
х 3 у 2 z 0,49
2
2
х у z 1
2
2
2
2
5.
6. Общее уравнение плоскости
7. Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору
Если известна какая-нибудь точкаn (A;B;C)
плоскости M0 и какой-нибудь
вектор нормали к ней, то через
M0
заданную точку можно провести
единственную плоскость,
перпендикулярную данному
вектору. Общее уравнение
плоскости будет иметь вид:
8. Упражнение 3. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .
: Используем формулуA(x-x0)+B(y-y0)+C(z-z0)=0
9. Уравнение прямой в пространстве
eПрямую, проходящую через точку A0(x0,y0,z0) с направляющим вектором
(a,b,c) можно задавать параметрическими уравнениями.
x at x0 ,
y bt y0 ,
z ct z .
0
В случае, если прямая в пространстве задается двумя точками
A1(x1,y1,z1), A2(x2,y2,z2), то, выбирая в качестве направляющего
вектора вектор (x2-x1,y2-y1,z2-z1) и в качестве точки А0 точку А1,
получим следующие уравнения
x ( x2 x1 )t x1 ,
y ( y2 y1 )t y1 ,
z ( z z )t z .
2
1
1
10. Упражнение 4
Напишите параметрические уравнения прямой,проходящей через точку А(1,-2,3) с направляющим
вектором, имеющим координаты (2,3,-1).
Ответ:
x 1 2t ,
y 2 3t ,
z 3 t.
11. Упражнение 5
Напишите параметрические уравнения прямой,проходящей через точки А1(-2,1,-3), А2(5,4,6).
Ответ:
x 2 7t ,
y 1 3t ,
z 3 9t.

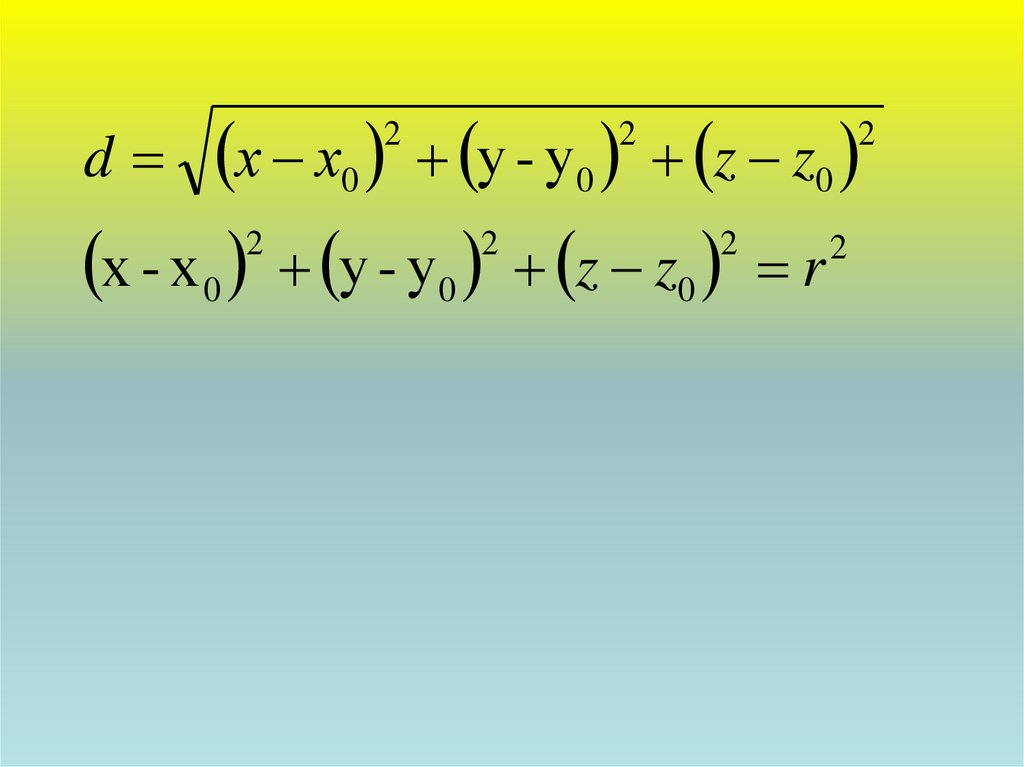









 mathematics
mathematics








