Similar presentations:
Логарифмические неравенства
1. Логарифмические неравенства
2. Вычислить (устно)
log 2 16; log 2 32; log 3 81; log 4 64;log 5 125; log 4 64; log 7 49; log 1 27;
3
1
1
log
; log
2 16
2 64
3.
• Пример №1.Решитьлогарифмическое
неравенство: log 2 х 3
4. РЕШЕНИЕ НЕРАВЕНСТВА:
1.В правой части , по определению логарифмапишем:
log2х ≥ log2 23
2. Составляем систему:(Первое неравенство: знак log
закрываем, второе: выражение всегда > 0, логарифмы
отрицательных чисел не существуют)
х 23 х 8
х 0 х 0
Смотрим на основание логарифма, оно равно 2, сраниваем его
с 1, 2 >1 значит, знак первого неравенства сохраняется, во
втором неравенстве всегда больше 0
5.
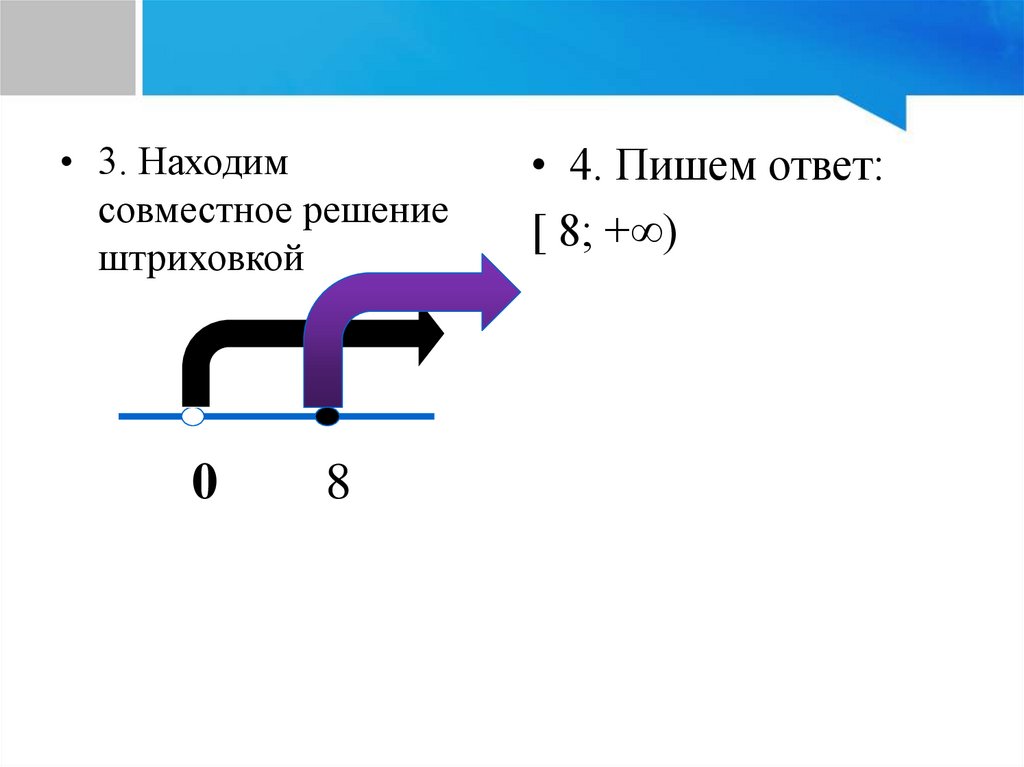
• 3. Находимсовместное решение
штриховкой
0
8
• 4. Пишем ответ:
[ 8; +∞)
6.
• Пример №2.Решитьлогарифмическое
неравенство: log 0,5 х 3
7. РЕШЕНИЕ НЕРАВЕНСТВА:
1.В правой части , по определению логарифмапишем:
log0,5х ≥ log 0,5 0,53
2. Составляем систему:(log закрываем)
3
1
1
3
х 0,5 х
х
8
2
х 0
х 0
х 0
Смотрим на основание логарифма, оно равно
0,5 , сраниваем с единицей, оно 0,5 < 1,значит
знак первого неравенства меняется на
противоположный, во втором неравенстве
всегда больше 0
8.
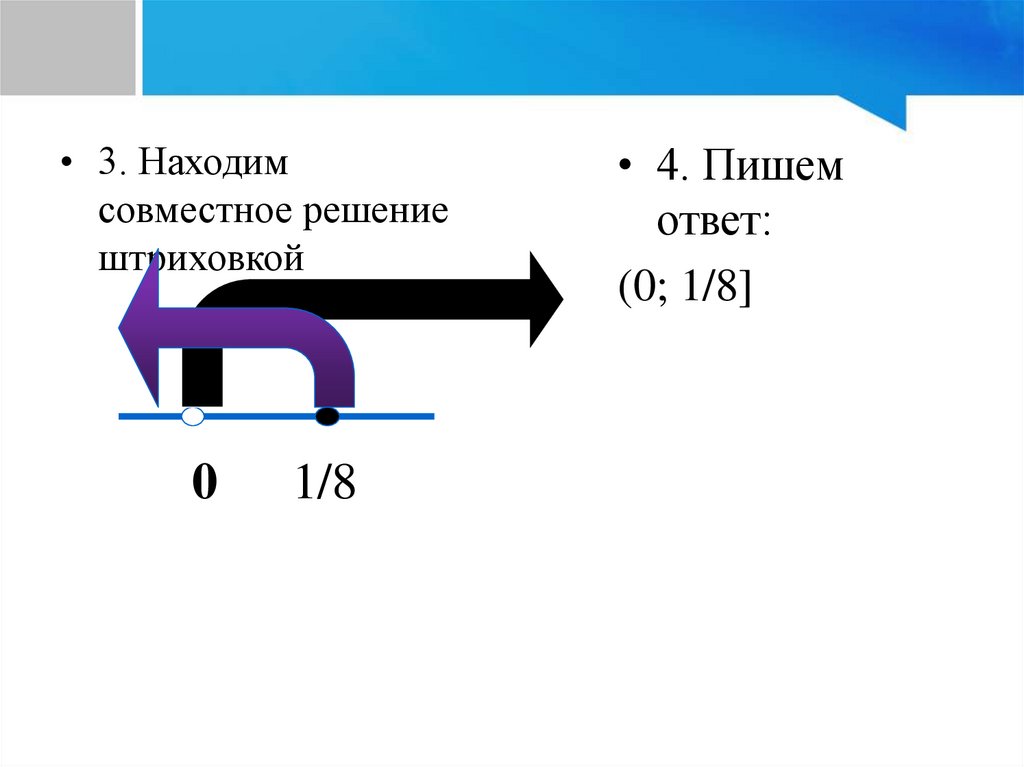
• 3. Находимсовместное решение
штриховкой
0
1/8
• 4. Пишем
ответ:
(0; 1/8]
9. Решить неравенства
1. log 5 х 12. log 4 2 х 2
3. log 0 , 5 8 х 2
4. log 0 , 25 4 х 1







 mathematics
mathematics








