Similar presentations:
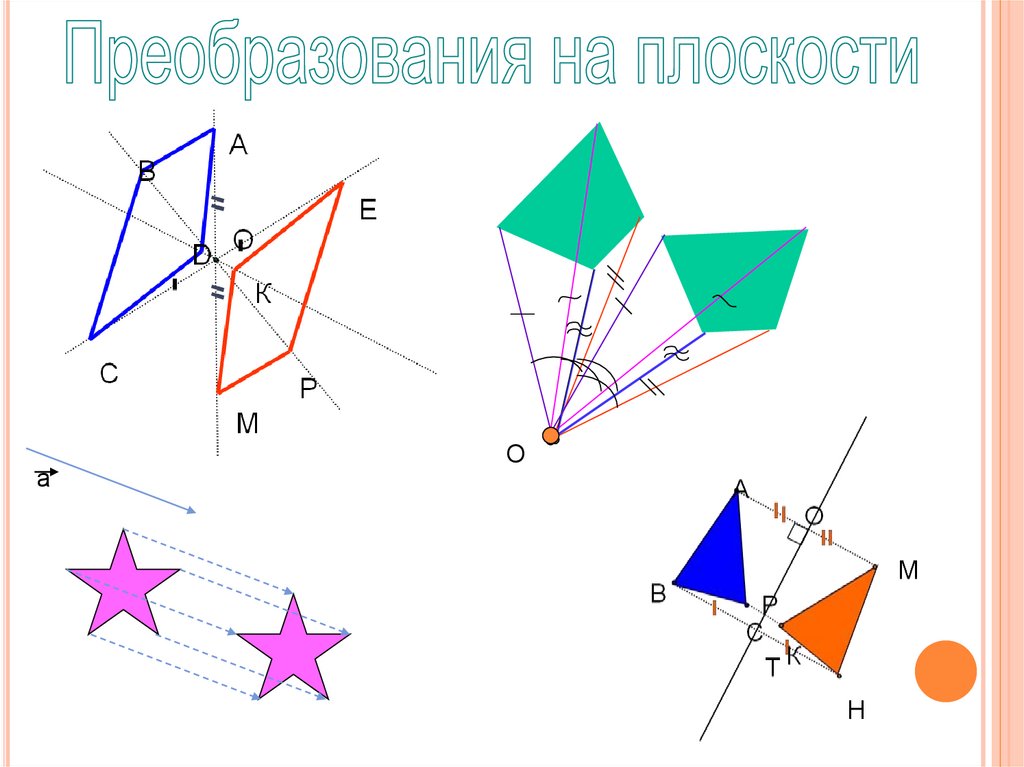
Преобразования на плоскости
1.
аО
2.
3.
Изучить, что такое поворот.Чем задаётся поворот?
Как обозначается?
Свойство поворота?
Научиться строить образы точек, фигур при
повороте вокруг т.О на угол α в заданном
направлении.
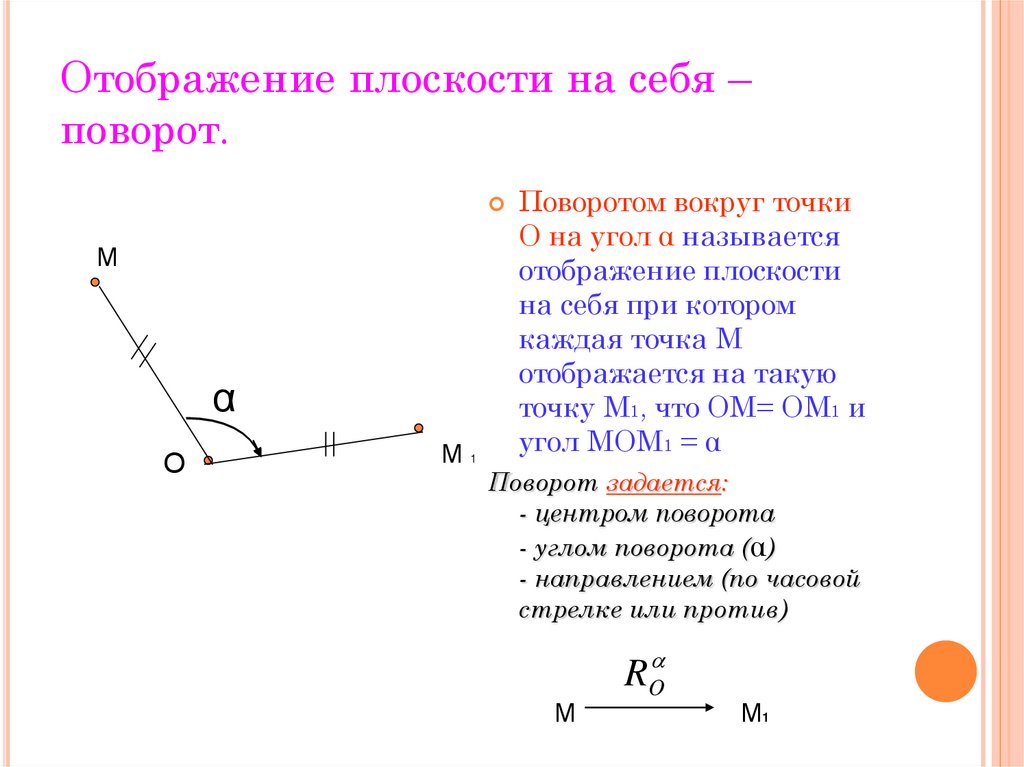
4. Отображение плоскости на себя – поворот.
Мα
О
М1
Поворотом вокруг точки
О на угол α называется
отображение плоскости
на себя при котором
каждая точка М
отображается на такую
точку М1, что ОМ= ОМ1 и
угол МОМ1 = α
Поворот задается:
- центром поворота
- углом поворота (α)
- направлением (по часовой
стрелке или против)
М
RO
М1
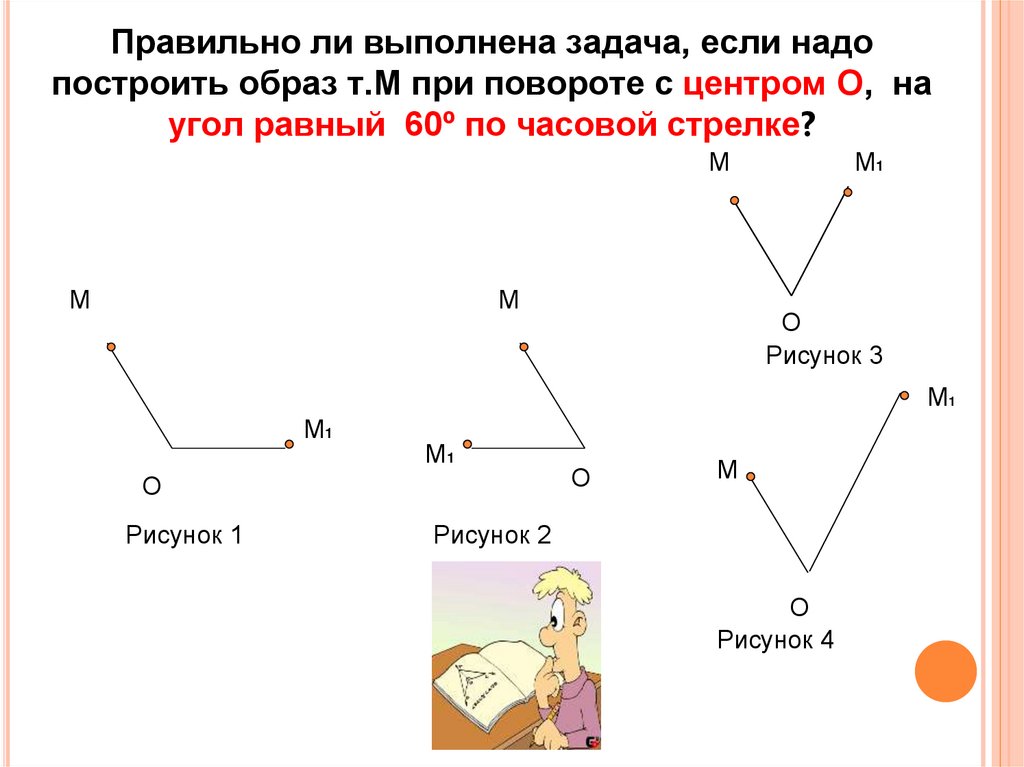
5. Правильно ли выполнена задача, если надо построить образ т.М при повороте с центром О, на угол равный 60º по часовой стрелке?
ММ
М
М1
О
Рисунок 3
М1
М1
М1
О
Рисунок 1
О
М
Рисунок 2
О
Рисунок 4
6.
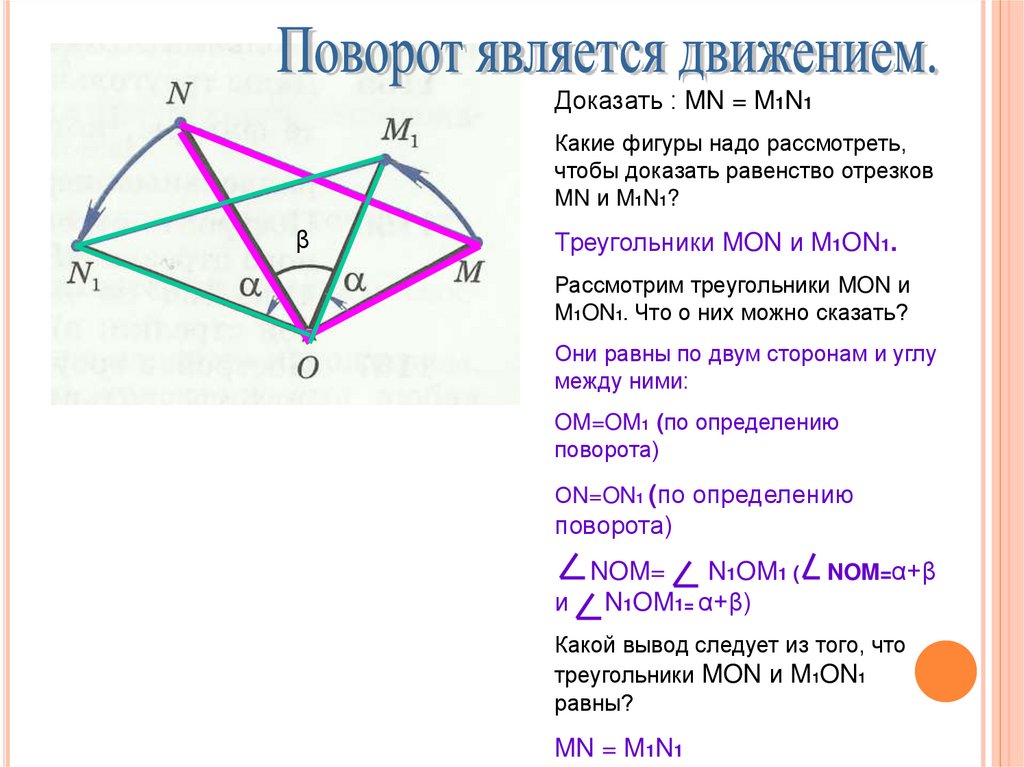
Доказать : MN = M1N1Какие фигуры надо рассмотреть,
чтобы доказать равенство отрезков
MN и M1N1?
β
Треугольники MON и M1ON1.
Рассмотрим треугольники MON и
M1ON1. Что о них можно сказать?
Они равны по двум сторонам и углу
между ними:
OM=OM1 (по определению
поворота)
ОN=ON1 (по определению
поворота)
NOM=
N1OM1 (
и N1OM1= α+β)
NOM=α+β
Какой вывод следует из того, что
треугольники MON и M1ON1
равны?
MN = M1N1
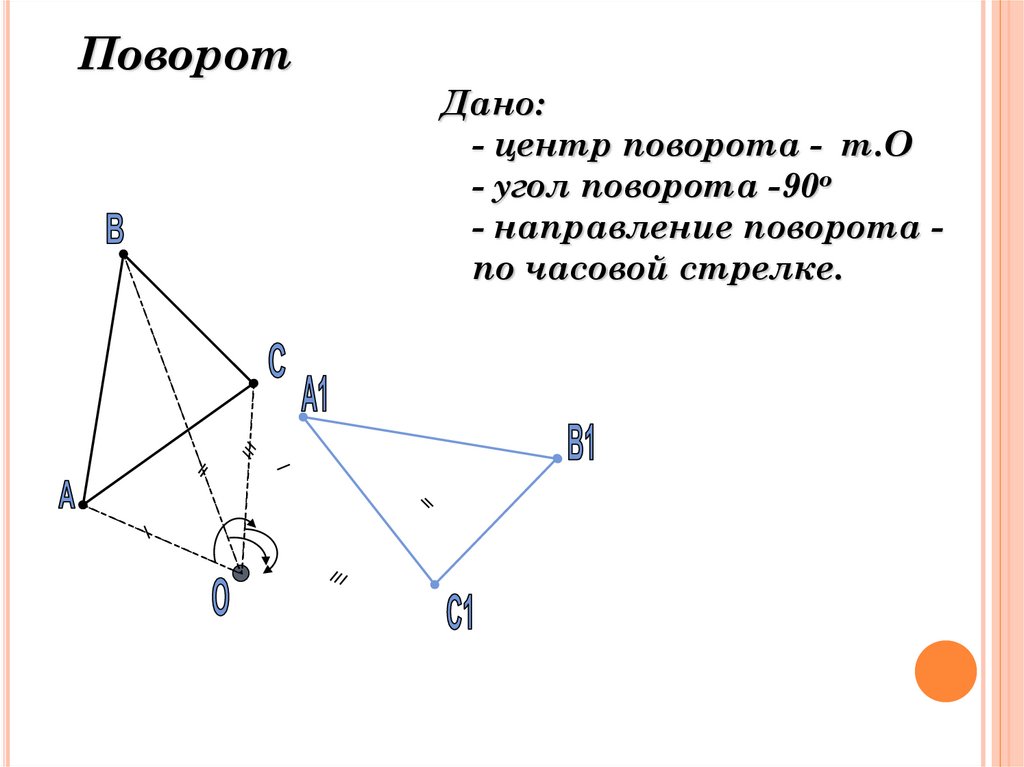
7. Поворот
Дано:- центр поворота - т.О
- угол поворота -90о
- направление поворота по часовой стрелке.
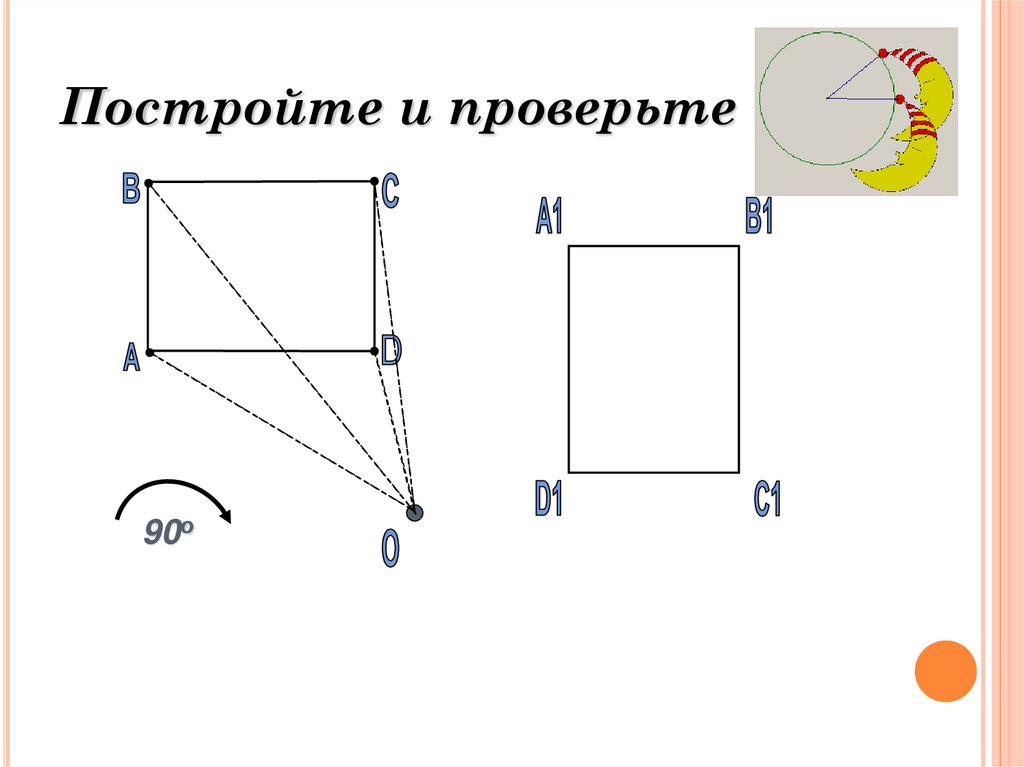
8. Постройте и проверьте
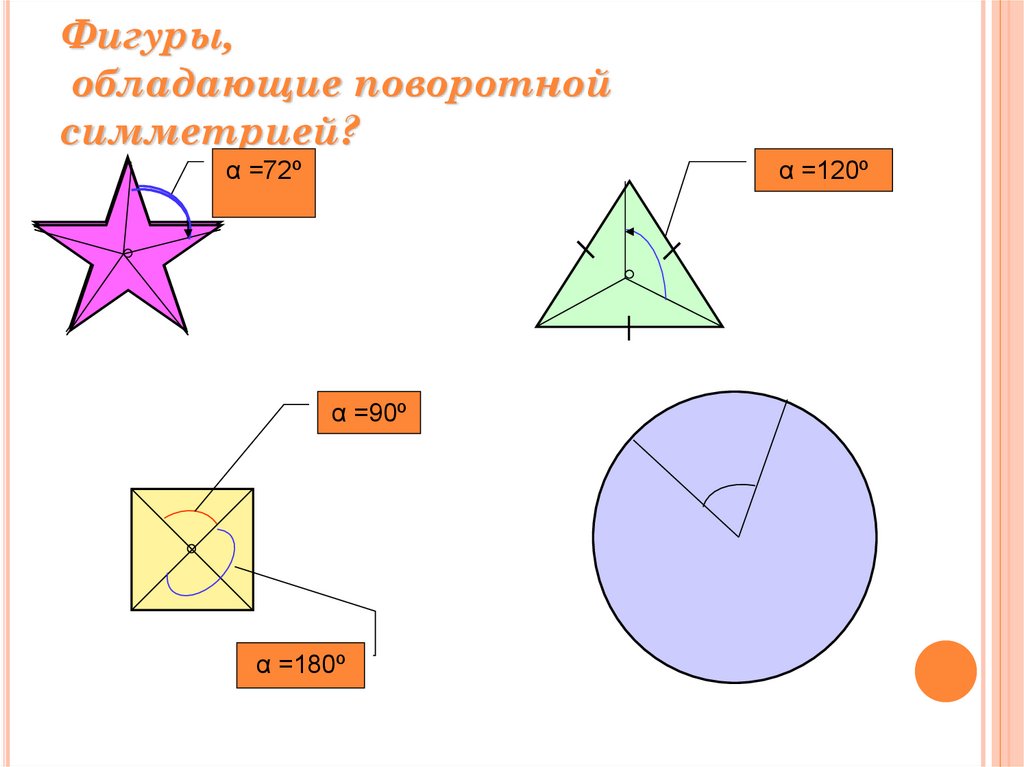
90о9. Фигуры, обладающие поворотной симметрией?
α =72ºα =120º
α =90º
α =180º
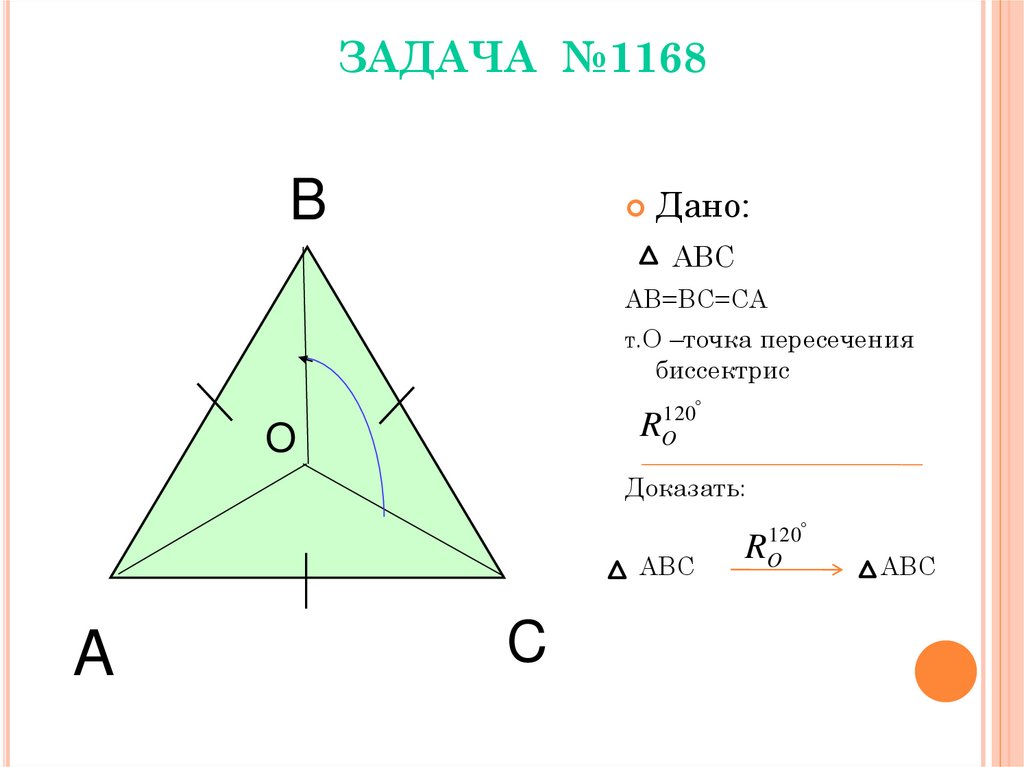
10. ЗАДАЧА №1168
BДано:
ABC
AB=BC=CA
Т
.O –точка пересечения
биссектрис
R
O
120
O
Доказать:
ABC
A
C
R
120
O
ABC
11.
Ответы к тесту№1
поворот
№2
№3
№4
№5
в, г
а
б
а, б, в
Какое впечатление получили от
урока?
Что нового для себя узнали?
Советы по построению.




 mathematics
mathematics








