Электрические трёхфазные цепи

1.

Содержание
1. Основные понятия и определения
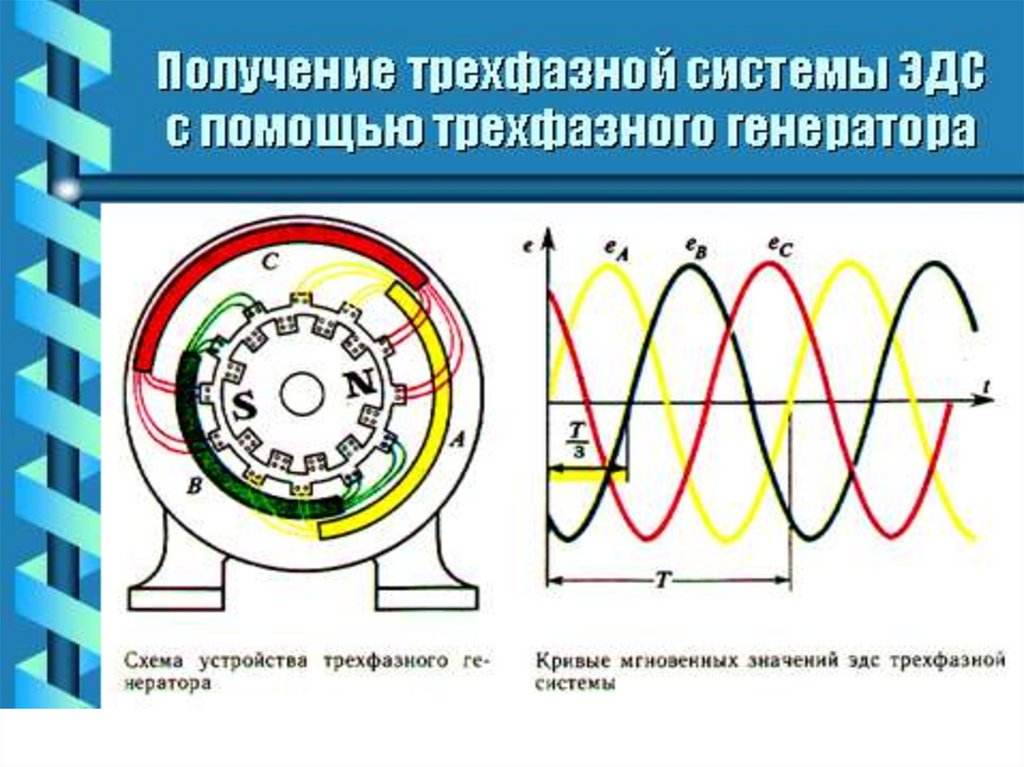
2. Получение трехфазной системы ЭДС
3. Соединение обмоток генератора и фаз приемника звездой
4. Трехфазный приемник, соединенный по схеме «звезда» (симметричный)
5. Трехфазный приемник, соединенный по схеме «звезда» (несимметричный)
6. Соединение фаз приемника звездой с нейтральным проводом
7. Соединение обмоток генератора и фаз приемника треугольником
8.Определение мощностей и коэффициента мощности 3-х фазного приемника
9. Получение вращающегося магнитного потока
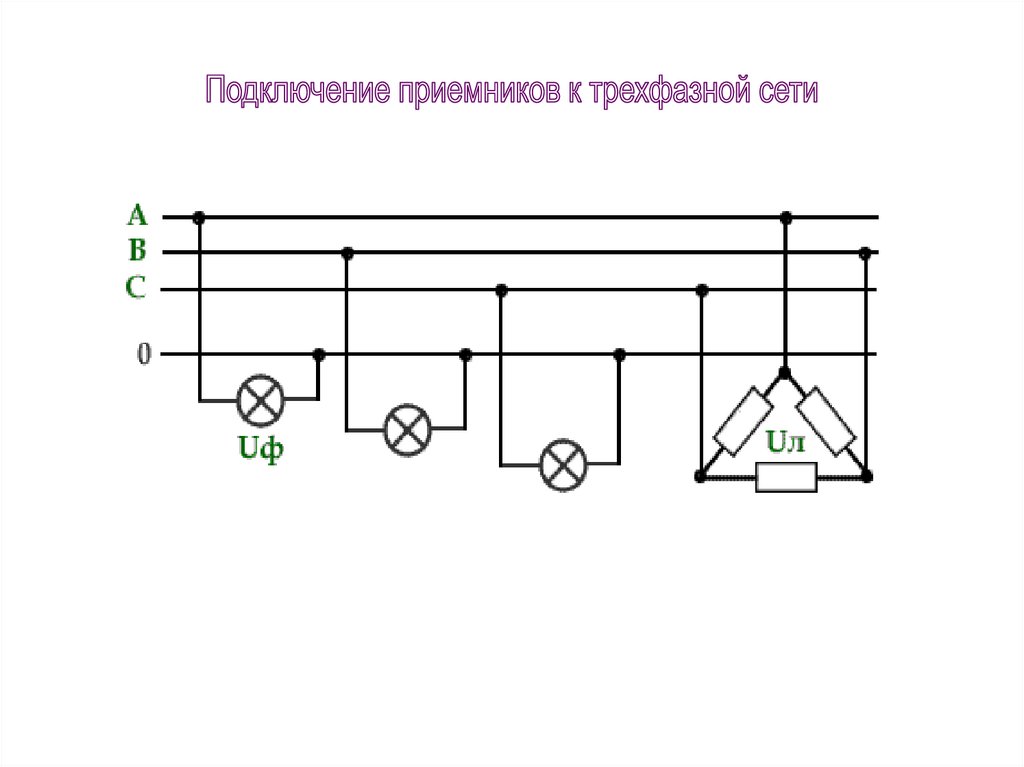
10. Подключение приемников к трехфазной сети

2.

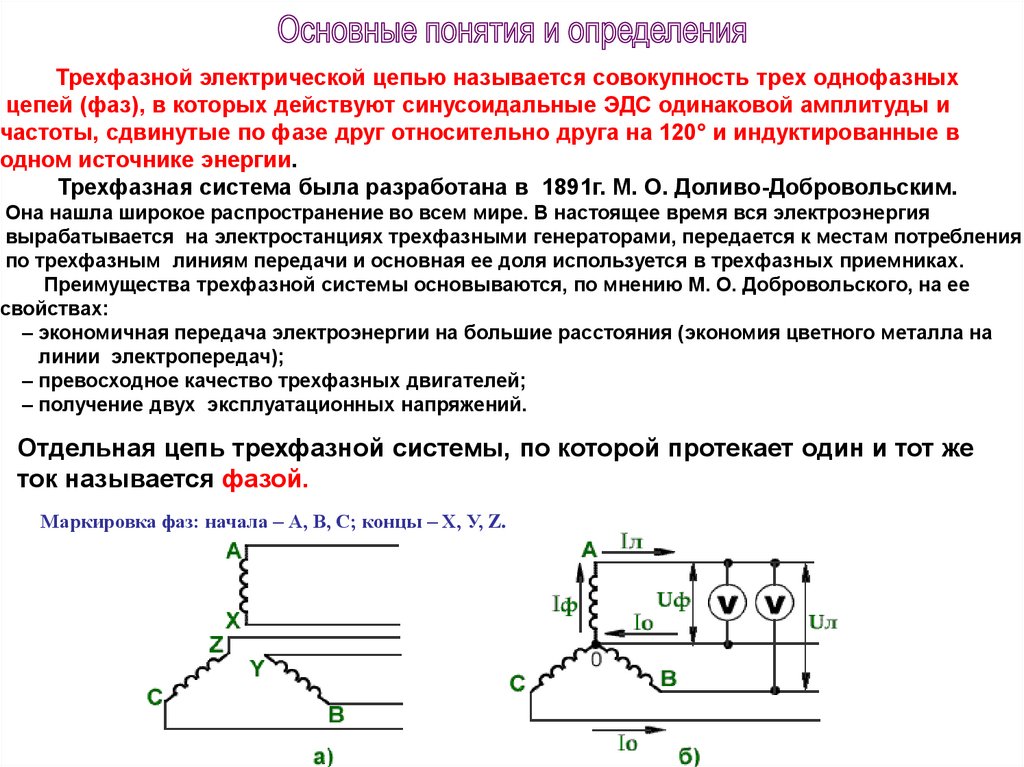
Трехфазной электрической цепью называется совокупность трех однофазных
цепей (фаз), в которых действуют синусоидальные ЭДС одинаковой амплитуды и
частоты, сдвинутые по фазе друг относительно друга на 120° и индуктированные в
одном источнике энергии.
Трехфазная система была разработана в 1891г. М. О. Доливо-Добровольским.
Она нашла широкое распространение во всем мире. В настоящее время вся электроэнергия
вырабатывается на электростанциях трехфазными генераторами, передается к местам потребления
по трехфазным линиям передачи и основная ее доля используется в трехфазных приемниках.
Преимущества трехфазной системы основываются, по мнению М. О. Добровольского, на ее
свойствах:
– экономичная передача электроэнергии на большие расстояния (экономия цветного металла на
линии электропередач);
– превосходное качество трехфазных двигателей;
– получение двух эксплуатационных напряжений.
Отдельная цепь трехфазной системы, по которой протекает один и тот же
ток называется фазой.
Маркировка фаз: начала – А, В, С; концы – Х, У, Z.

3.

4.

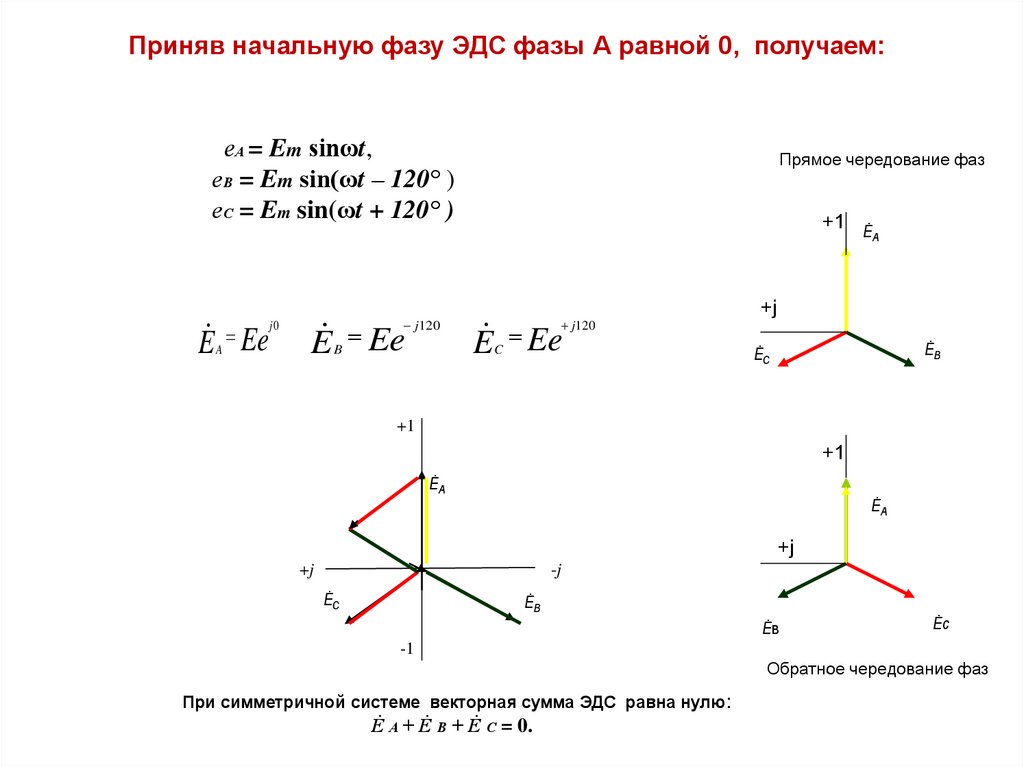
Приняв начальную фазу ЭДС фазы А равной 0, получаем:
еА = Em sinωt,
еВ = Em sin(ωt – 120° )
еС = Em sin(ωt + 120° )
E Ee
A
j0
E
j120
B
Ee
Прямое чередование фаз
+1 Ė
A
j120
E Ee
C
+j
ĖB
ĖC
+1
+1
ĖA
ĖA
+j
+j
-j
ĖC
ĖB
Ėв
Ėс
-1
Обратное чередование фаз
При симметричной системе векторная сумма ЭДС равна нулю:
Ė А + Ė В + Ė С = 0.

5.

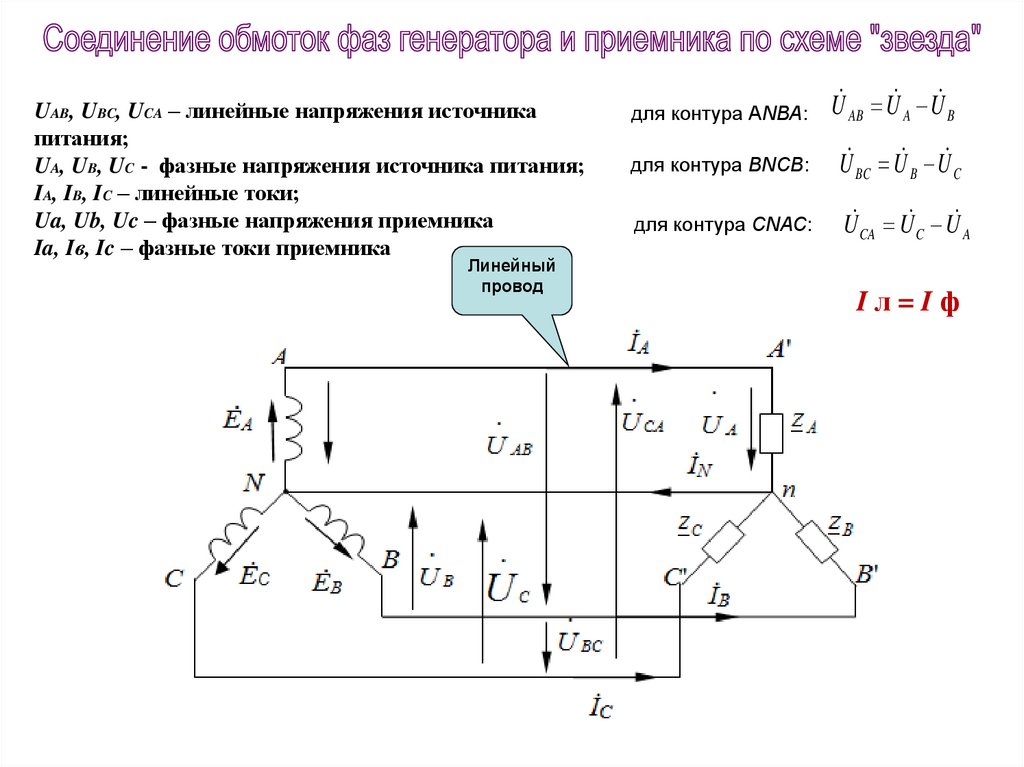
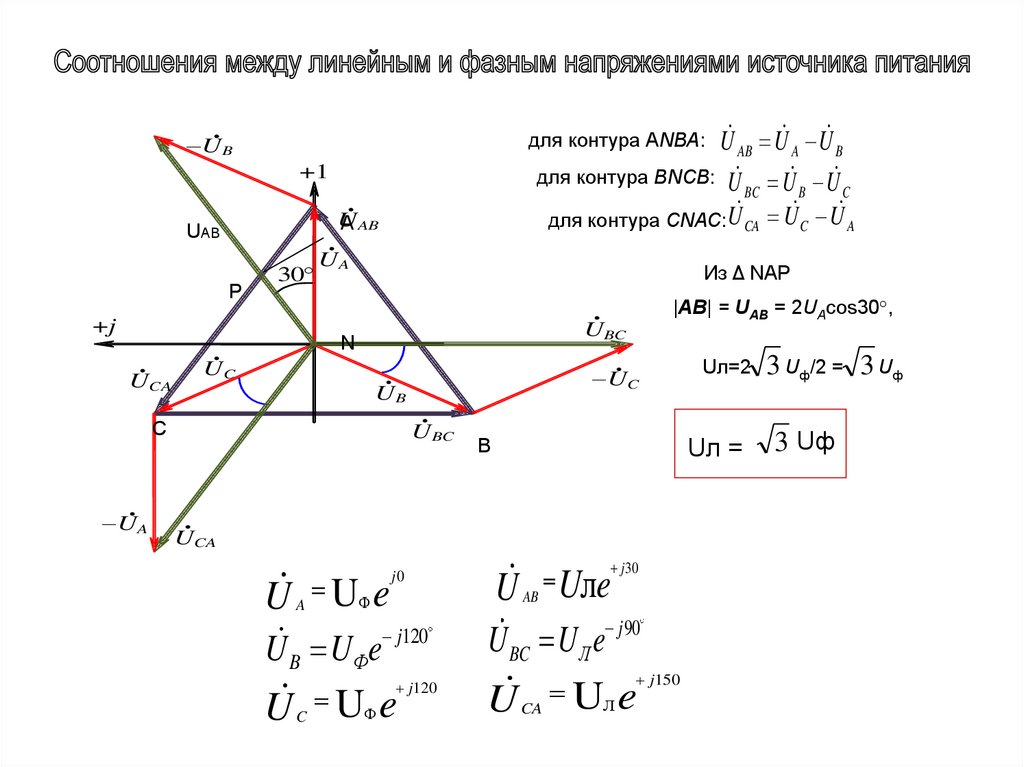
UAB, UBC, UCA – линейные напряжения источника
питания;
UA, UB, UC - фазные напряжения источника питания;
IA, IB, IC – линейные токи;
Ua, Ub, Uc – фазные напряжения приемника
Ia, Iв, Ic – фазные токи приемника
Линейный
провод
для контура АNВА:
U AB U A U B
для контура ВNСВ:
U BC U B U C
для контура СNАС:
U CA U C U A
Iл=Iф

6.

U AB U A U B
для контура ВNСВ: U U U
BC
B
C
для контура СNАС: U CA U C U A
.
–UB
для контура АNВА:
+1
.
U
А AB
UАВ
P
30
+j
.
UCA
.
UA
Из Δ NАР
N
.
UC
.
–UC
.
UB
.
UBC
С
.
–UA
|АВ| = UАВ = 2UАcos30°,
.
UBC
Uл =
В
.
UCA
U U e
A
j120
j120
C
U Uлe
j 30
AB
Ф
U B UФ e
U
j0
UФ e
Uл=2
U BC U Л e j 90
U
j150
UЛ e
CA
3 Uф/2 = 3 Uф
3 Uф

7.

В промышленности пользуются напряжением 127, 220 и 380 В.
В высоковольтных линиях электропередачи применяют напряжение 6 кВ,
10 кВ, 35 кВ, 110 кВ, 220 кВ, 400 кВ, 500 кВ и более.
В низковольтных установках применяются, как правило, четырехпроводные линии электропередачи, а в высоковольтных - трехпроводные.
Четырехпроводные линии удобны при совместном электропитании
силовых и осветительных потребителей.
Электродвигатели, например, подключаются к трем линейным проводам,
а осветительные приборы - к одному линейному и нулевому проводам.
При электроснабжении жилых домов в них вводят четырехпроводный
кабель. В квартиры же подается один нулевой провод и один линейный.
При этом линейные провода чередуются от квартиры к квартире.
Это необходимо для того, чтобы наиболее равномерно загрузить сеть
по фазам.

8.

Симметричный трехфазный приемник
это приемник, у которого
комплексные сопротивления фаз равны между собой т.е.
Za Zb Zc
C
A
Za = Zв = Zc,
= =
а
в
с.
U A U B UC 0.
B
Согласно схеме четырехпроводной системы:
IC
IA
IB
U a U nN U A 0,
Ub U nN U B 0,
Za
U c U nN UC 0.
Напряжения фаз приемника:
Z
c
Zb
n
U a U A U nN ,
Ub U B U nN ,
Так как
Ua U A
U c UC U nN .
UnN = 0,то
Ub U B
Uc UC
Фазные токи:
İа = U a / Z a
İb = U b / Z b
İс = U c / Z c
İа + İb + İс = 0
.

9.

.
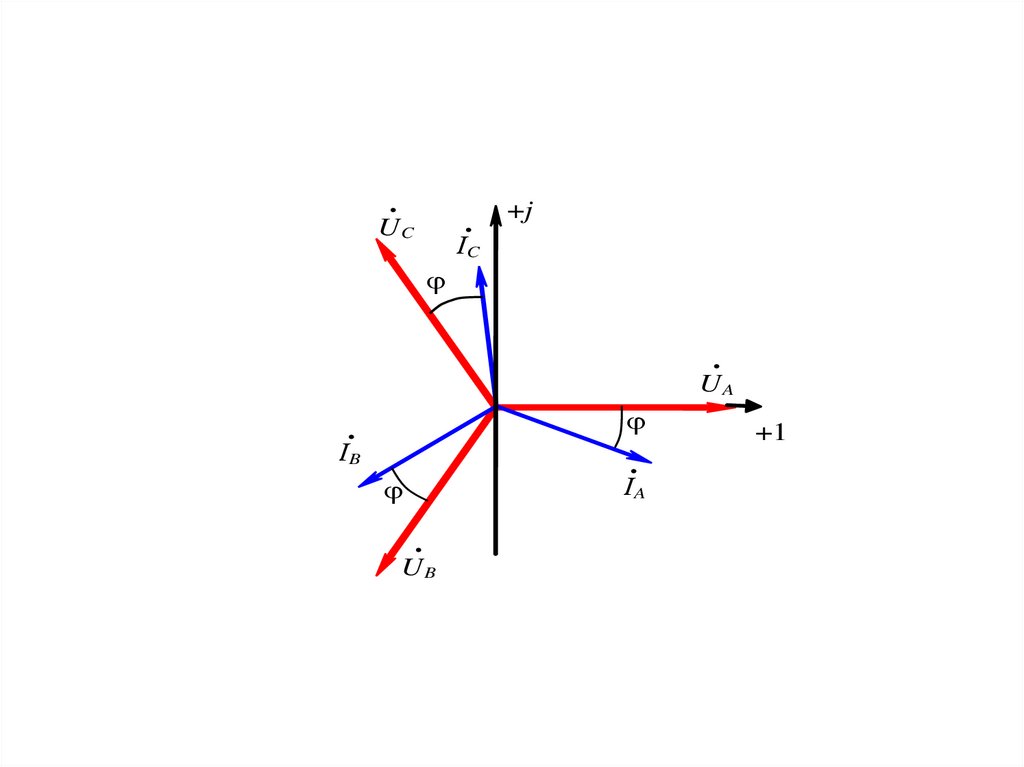
UC
.
ІC
+j
.
UA
.
ІB
.
UB
.
ІA
+1

10.

Несимметричный трехфазный приемник – это приемник, у которого
комплексные сопротивления фаз не равны между собой, т.е.
C
A
B
Za Zb Zc
Z a Zb Z c , а ≠ b ≠ c общий случай,
Z a Zb Z c , а ≠ b ≠ c равномерная несимметричная
R
Z a Zb Zc , а = b = c однородная несимметричная.
XC
n
XL
Проводимости фаз:
Y a 1/ Z a 1/ R
Y 1/ Z 1/( X Le j 90 )
b
b
Yc 1/ Zc 1/( X ce
j 90
)

11.

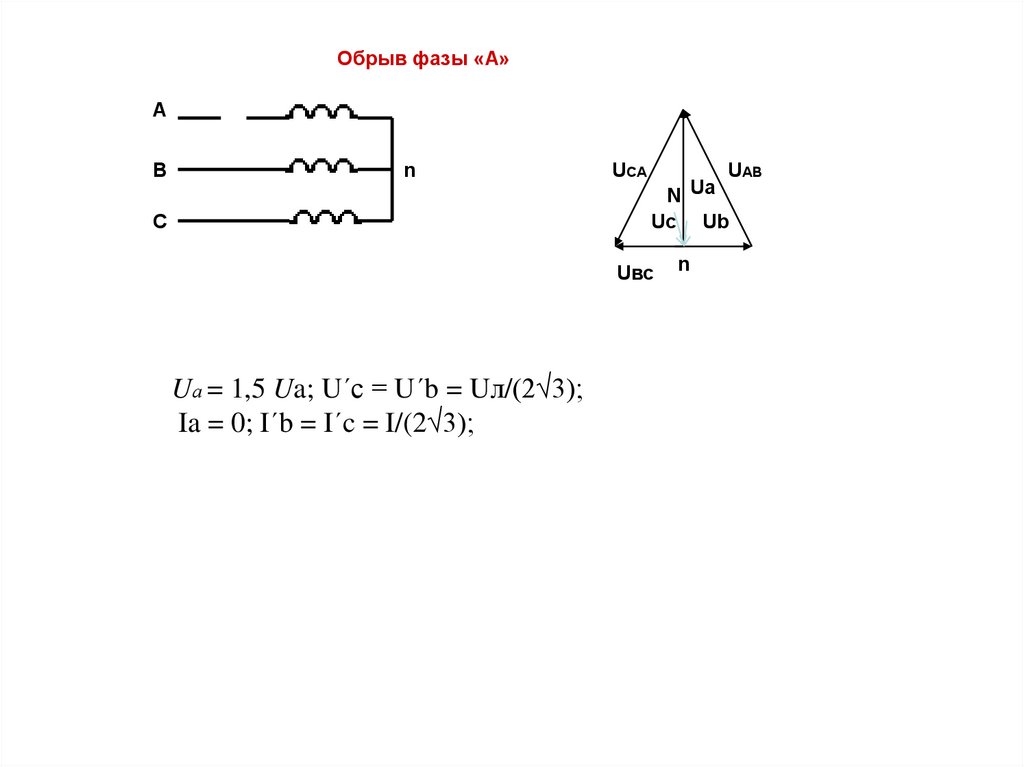
Обрыв фазы «А»
А
В
n
С
UCA
UAB
Uа
N
Uс Ub
Uвс
Uа = 1,5 Ua; U´с = U´b = Uл/(2√3);
Ia = 0; I´b = I´c = I/(2√3);
n

12.

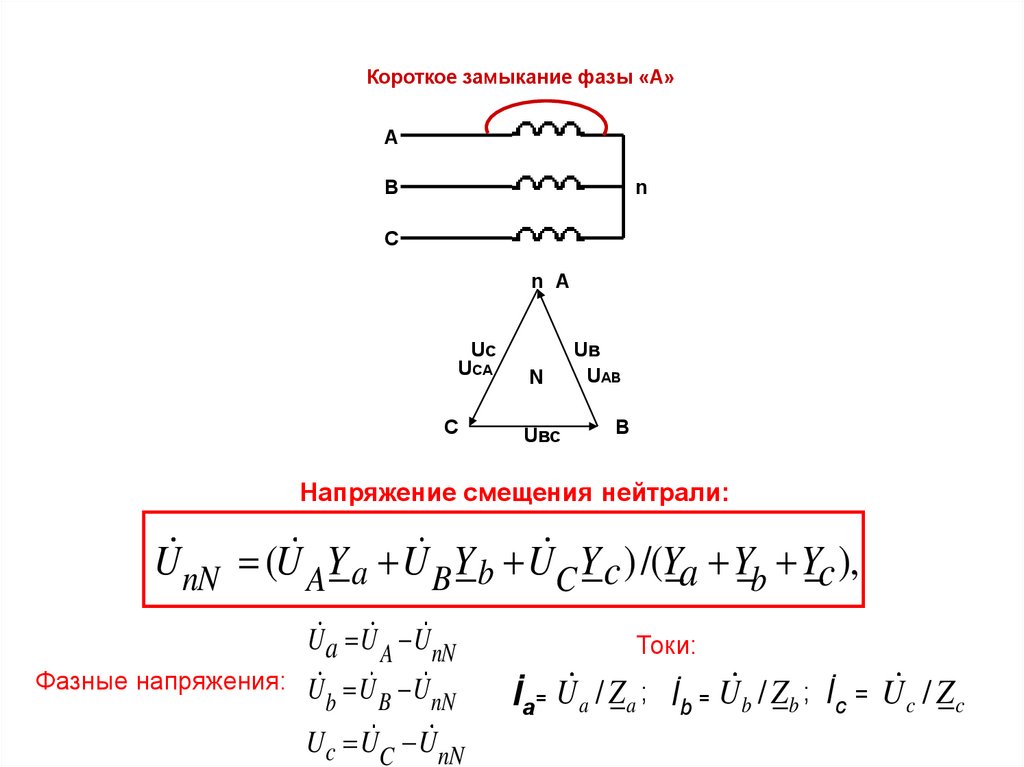
Короткое замыкание фазы «А»
А
В
n
С
n A
Uс
UCA
C
N
Uвс
Uв
UAB
B
Напряжение смещения нейтрали:
U nN (U AY a U B Y b UC Y c )/(Ya Yb Yc ),
Ua U A UnN
Фазные напряжения: U U U
B
nN
b
Uc UC UnN
Токи:
İ а= U a / Z a ; İ b = U b / Z b ; İ с = U c / Z c

13.

+j'
C
A
.
ІC
B
R
XC
n
n
XL
.
ІB
B .
ІC
+j
C .
Uc
.
UC
+1'
.
ІA
UnN
N
N
. .
ІBUb
.
UB
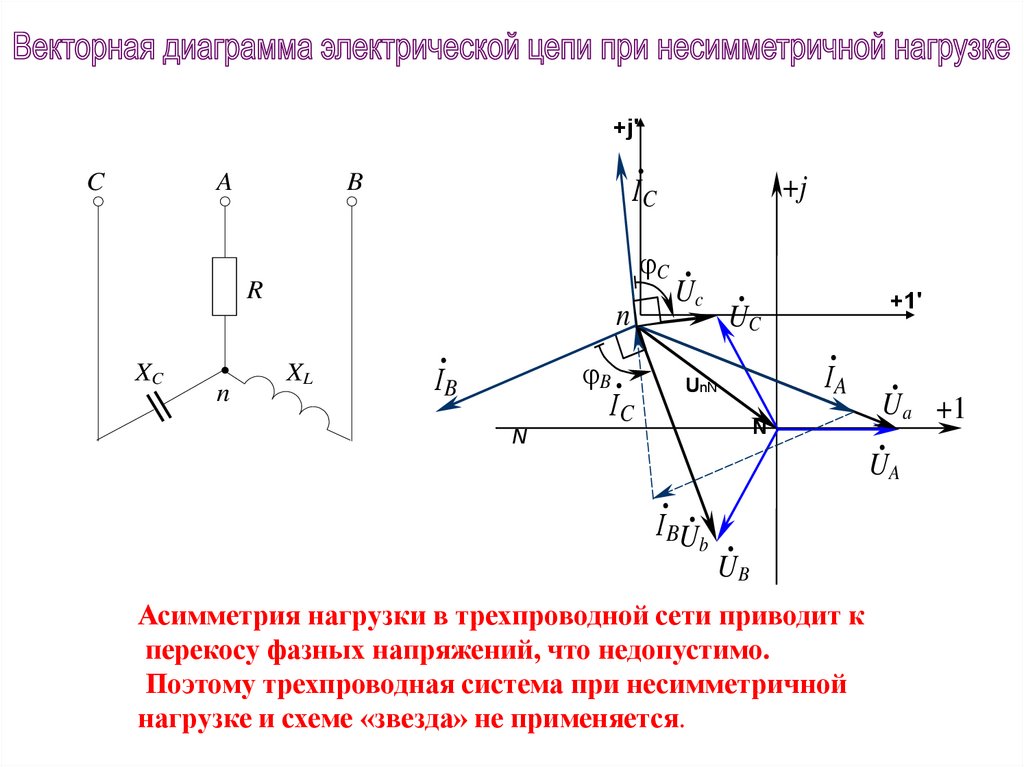
Асимметрия нагрузки в трехпроводной сети приводит к
перекосу фазных напряжений, что недопустимо.
Поэтому трехпроводная система при несимметричной
нагрузке и схеме «звезда» не применяется.
.
Ua +1
.
UA

14.

Для выравнивания фазных напряжений приемника необходимо получить
значение напряжения между нейтральными точками генератора и
приемника равное 0. Это возможно при включении нейтрального провода
между нейтралями генератора и приемника. Сопротивление этого провода
не более 4 Ом.
U AY a U B Y b UC Y c
U nN
0
Y a Y b Y c Y nN
;
C
A
B
N
Тогда:
IC
IA
IB
;
,
R
IN
n
XC
XL
Ua U A
Ub U B
U c UC

15.

.
UC
+j
.
ІB
.
ІB
.
ІC
.
Іn
C
.
UA
iN
B
.
ІC
+1
.
ІA
.
UB
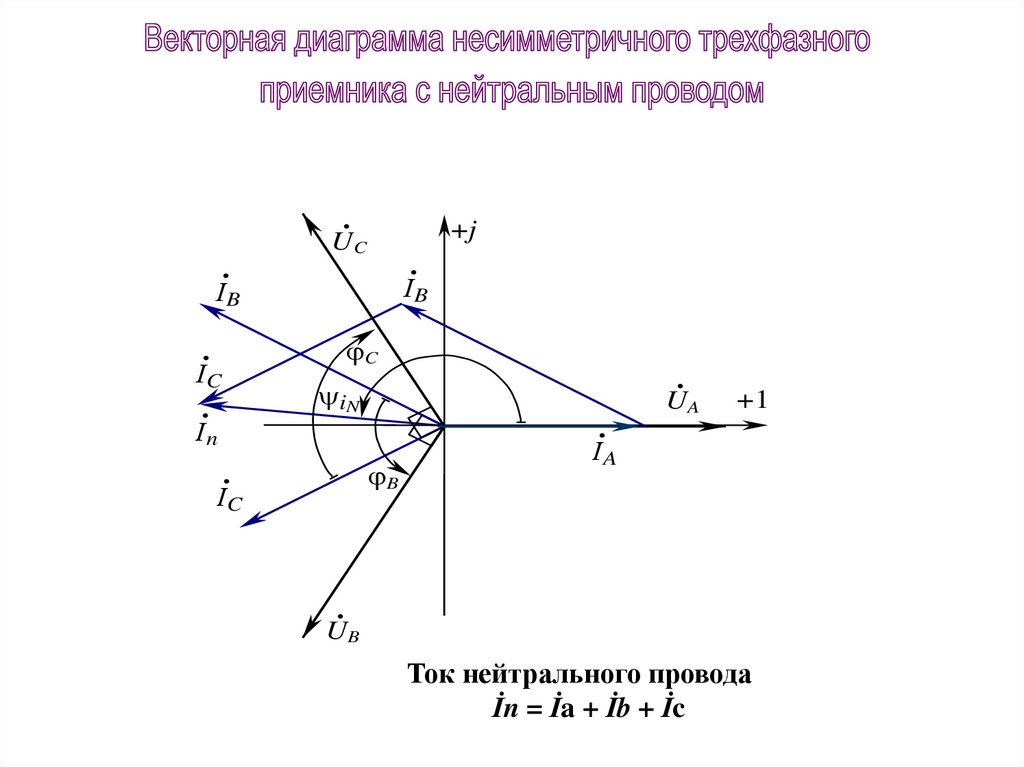
Ток нейтрального провода
İn = İa + İb + İc

16.

a
İA
İab
İca
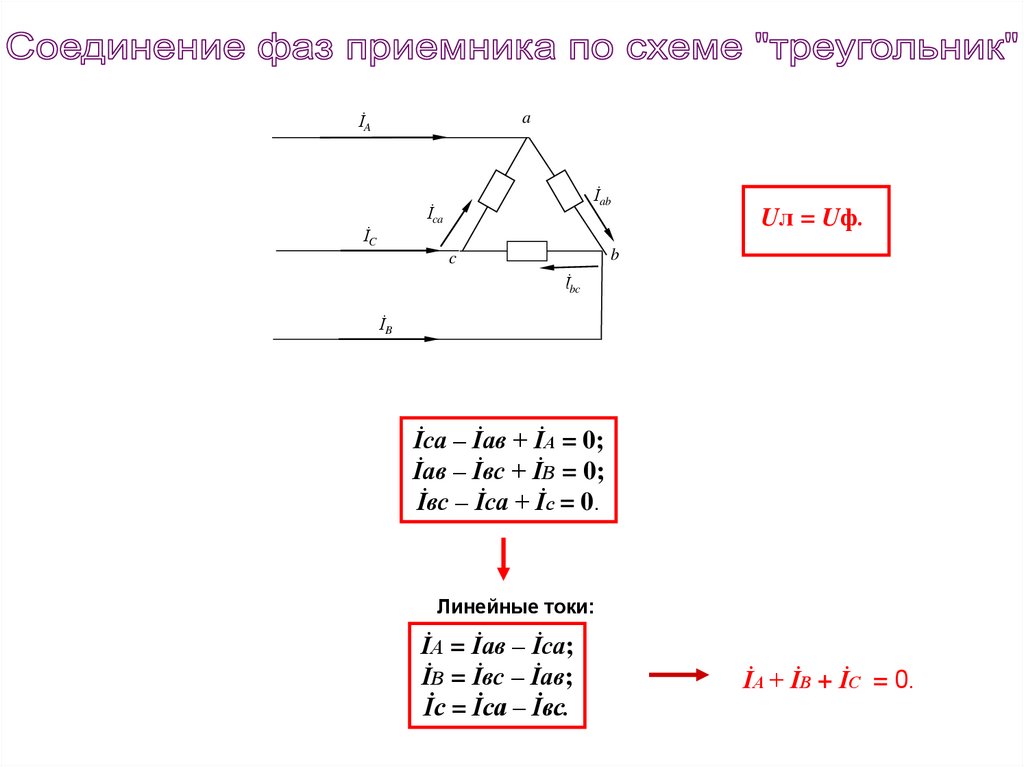
Uл = Uф.
İC
b
c
İbc
İB
İса – İав + İА = 0;
İав – İвс + İВ = 0;
İвс – İса + İс = 0.
Линейные токи:
İА = İав – İса;
İВ = İвс – İав;
İс = İса – İвс.
İА + İВ + İС = 0.

17.

A
İB
İab
İA
30˚
İca
İbc
C
B
а)
İC
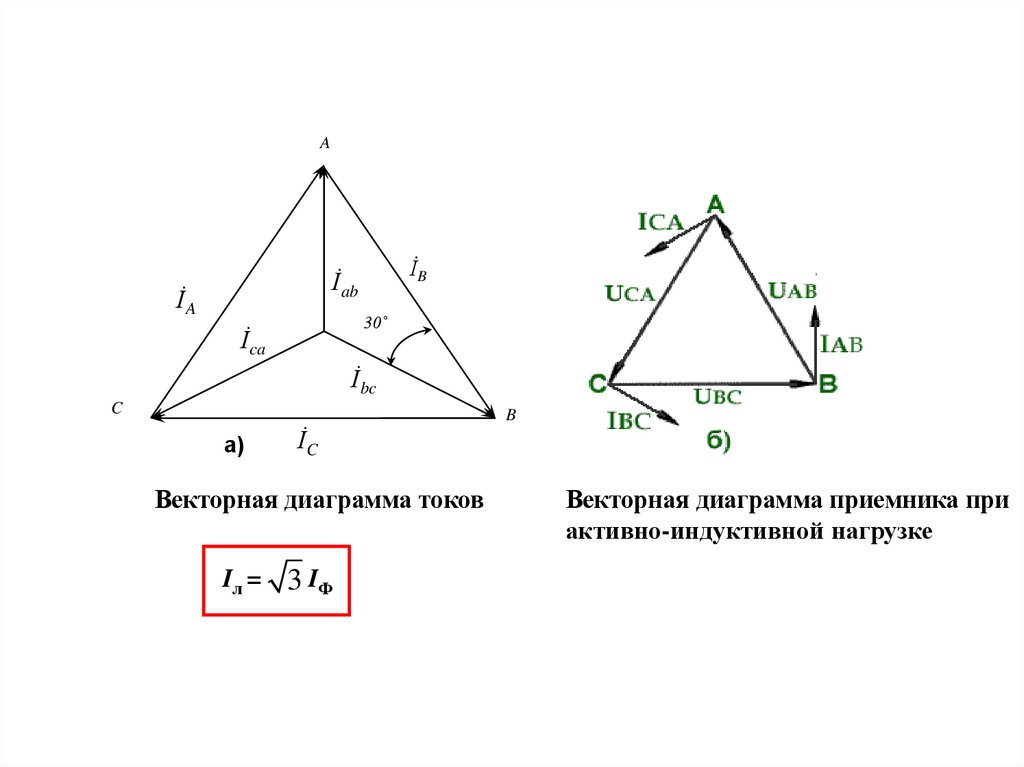
Векторная диаграмма токов
Iл =
3 IФ
Векторная диаграмма приемника при
активно-индуктивной нагрузке

18.

Трехпроводная система. При соединении треугольником Uл = Uф, а линейные
напряжения источника всегда симметричны. Поэтому соединение треугольником
применяется в трехпроводных системах при любой нагрузке, как симметричной,
так и несимметричной, если номинальное напряжение приемника равняется
линейному напряжению источника питания.
Z ab Re j 0
C
A
B
IA
IC
IB
a
Z bc X Le j 90
Z ca X C e j 90
Iab
Ica
XC
R
XL
c
U
I Z
j0
j0
U e U e
I e
j0
R
Z
Ue
U
I e
I Z
Z
ф
ab
ф
j0
ab
ab
ab
j120
ca
j 210
ф
- j90
ca
ca
b
Ibc
Примем AB 0
ca
U
I Z
j120
bc
bc
bc
Uфe
j 210
I bc e
j90
Z

19.

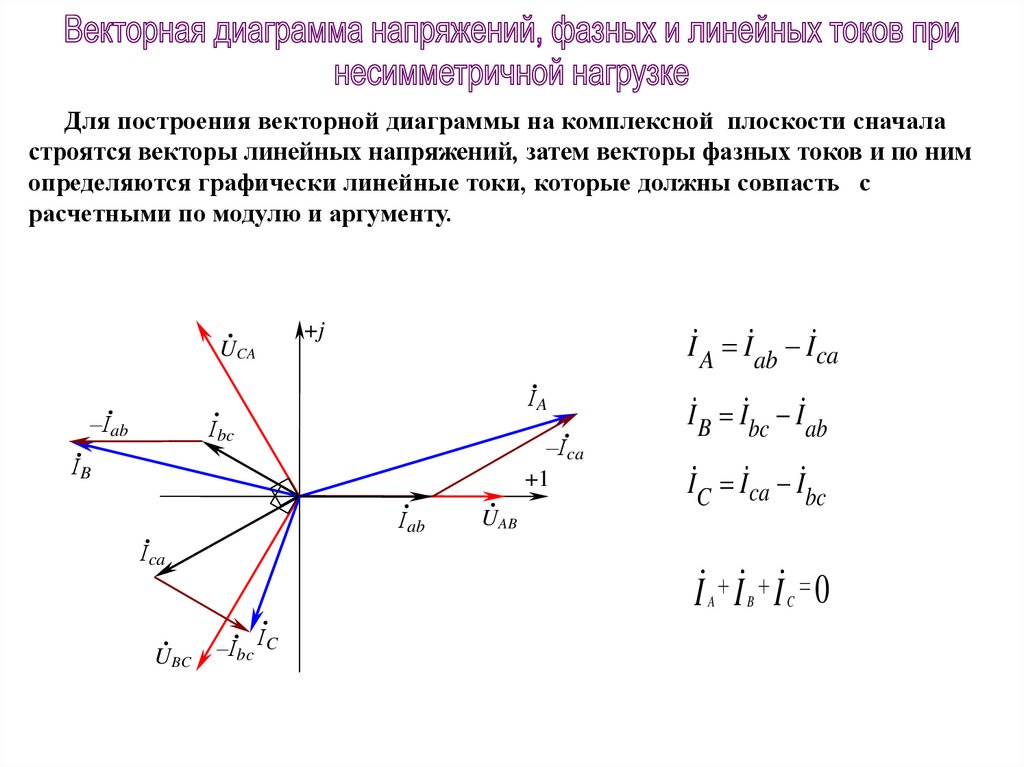
Для построения векторной диаграммы на комплексной плоскости сначала
строятся векторы линейных напряжений, затем векторы фазных токов и по ним
определяются графически линейные токи, которые должны совпасть с
расчетными по модулю и аргументу.
.
UCA
.
–Іab
+j
.
ІA
.
Іbc
.
ІB
.
Іab
.
Іca
.
UBC
.
. ІC
–Іbc
.
UAB
.
–Іca
+1
I A I ab Ica
I B Ibc I ab
IC Ica Ibc
I I I 0
A
B
C

20.

При симметричной нагрузке фаз приемника:
Za Zb Zc
Полная мощность S, ВА:
S = 3Sф = 3UфIф =
φ
Активная мощность Р, Вт: Р = 3Р3ф = 3UфIфcos
3 UлIл
=
Реактивная мощность Q, вар: Q = 3Qф =3UфIфsin
3 UлIлcos φ
=
3 UлIл sin
Коэффициент мощности соs P / S
При несимметричной нагрузке фаз
Za Zb Zc
Полная мощность трехфазной цепи определяется как геометрическая сумма мощностей
фаз:
S=
Активная мощность:
Реактивная мощность
,ВА
P Pa Pb Pc ,Вт
Q Qa Qb Qc ,вар

21.

А
Y
А
+
+
120°
Ф
Z
+
Ф
В
t1
б)
Y
+
C
120° 120°
+
Z
+
C
t2
Х
Х
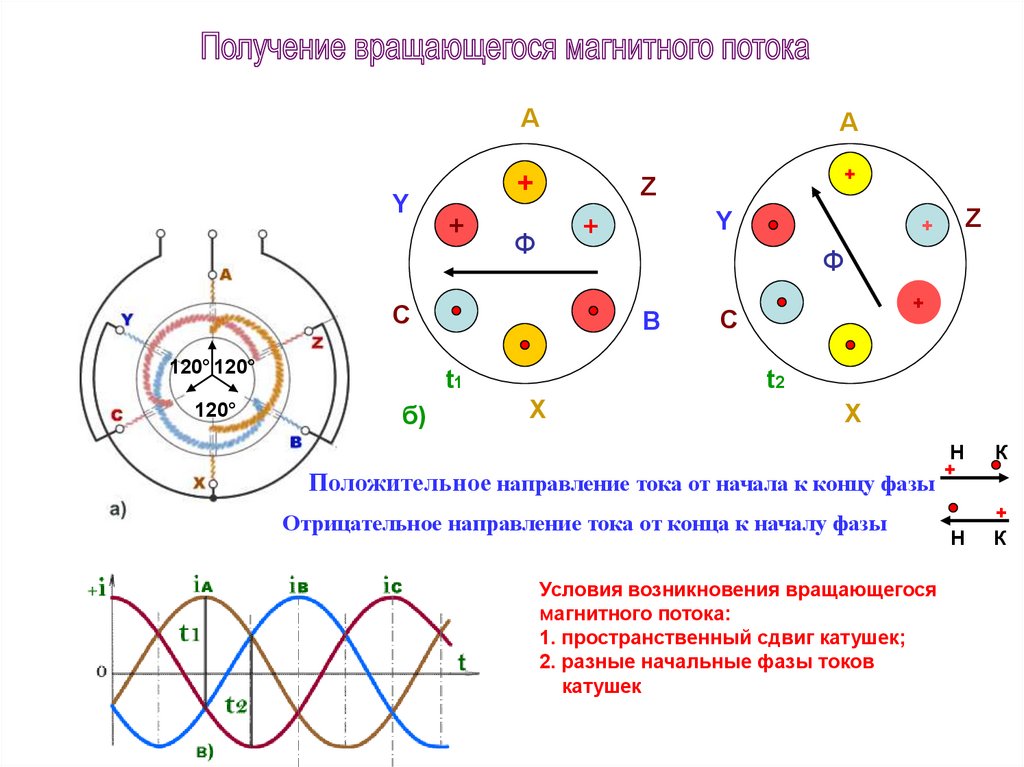
Положительное направление тока от начала к концу фазы
Отрицательное направление тока от конца к началу фазы
Условия возникновения вращающегося
магнитного потока:
1. пространственный сдвиг катушек;
2. разные начальные фазы токов
катушек
Н
+
Н
К
+
К

22.

23.

Задача .
В четырехпроводную сеть с линейным напряжением Uл =220 В ψUа=0, включен трехфазный
приемник, соединенный по схеме «звезда» с нейтральным проводом. Комплексные
сопротивления фаз приемника:
Z a 3 j 4; Z ab 3 j5,2; Z ac 4 j3;
Найти комплексные токи в линейных и нейтральном проводах.
Решение.
Фазное напряжение, В:
U
ф
U
л
3
220
3
127
Комплексные фазные напряжения, В:
0
0
0
0
U a 127e j 0 ; U b 127e j120 ; U c 127e j 240 127e j120 ;
Комплексные линейные токи равны соответственно комплексным фазным токам, А:
I I U a
A
a
za
I I U b
B
b
zb
I I U c
C
c
zc
127e j 0
3 4 e
2
2
0
jarctg
4
3
127e j120
0
32 5,2 2 e
127e
j1200
4 2 32 e
0
25,4e j 53
0
0
5e j 53
127e j120
0
5, 2
jarctg
3
jarctg
127e j 0
3
4
0
6e j 60
127e
5e
j1200
j 370
21,2e j180
0
25,4e
j 830

24.

Комплексный ток в нейтральном проводе, А:
I N I a I b I c 25,4e
j 530
21,2e
j1800
25,4e
j 830
I N (25,4 cos( 530 ) j 25,4 sin( 530 )) (21,2 cos( 1800 ) j 21,2 sin( 1800 ))
(25,4 cos 830 j 25,4 sin 830 ) 2,81 j 4,9 5,9e j120

25.

1. К трехфазной линии с Uл = 220 В подключен трехфазный приемник,
соединенный по схеме: а) «звезда» с нейтральным проводом;
б) «треугольник». Сопротивления фаз приемника Ra = 10 Ом, Rb = 3 Ом,
Хb = 4 Ом, XC = 10 Ом. Определить линейные и фазные токи,
активную, реактивную, полную мощности трехфазного приемника,
коэффициент мощности. Построить векторную диаграмму напряжений и
токов на комплексной плоскости.
2. К трехфазной линии с Uл = 220 В подключен симметричный трехфазный
приемник, активная потребляемая мощность которого P = = 5 кВт,
cosφ = 0,6. Определить токи приемника при соединении фаз по схеме
«звезда», «треугольник». Определить сопротивление фазы приемника.
Построить совмещенную векторную диаграмму токов и напряжений
3. Приемник соединен по схеме «звезда» с нейтральным проводом. В фазу
А включен реостат R, в фазу В катушка L, R, в фазу C конденсатор С.
Начертите электрическую схему и построить векторную диаграмму токов
и напряжений.
4. Вычертите электрическую схему и построить векторную диаграмму
напряжений и токов для трехфазного приемника, соединенного по схеме
«треугольник», если в первую фазу включен элемент с параметром L, во
вторую с параметром C, в третью с параметром R.