Трёхфазные электрические цепи. Лекция 7

1. БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова кафедра электротехники, О8

Лекция 7
Трёхфазные электрические цепи
1

2.

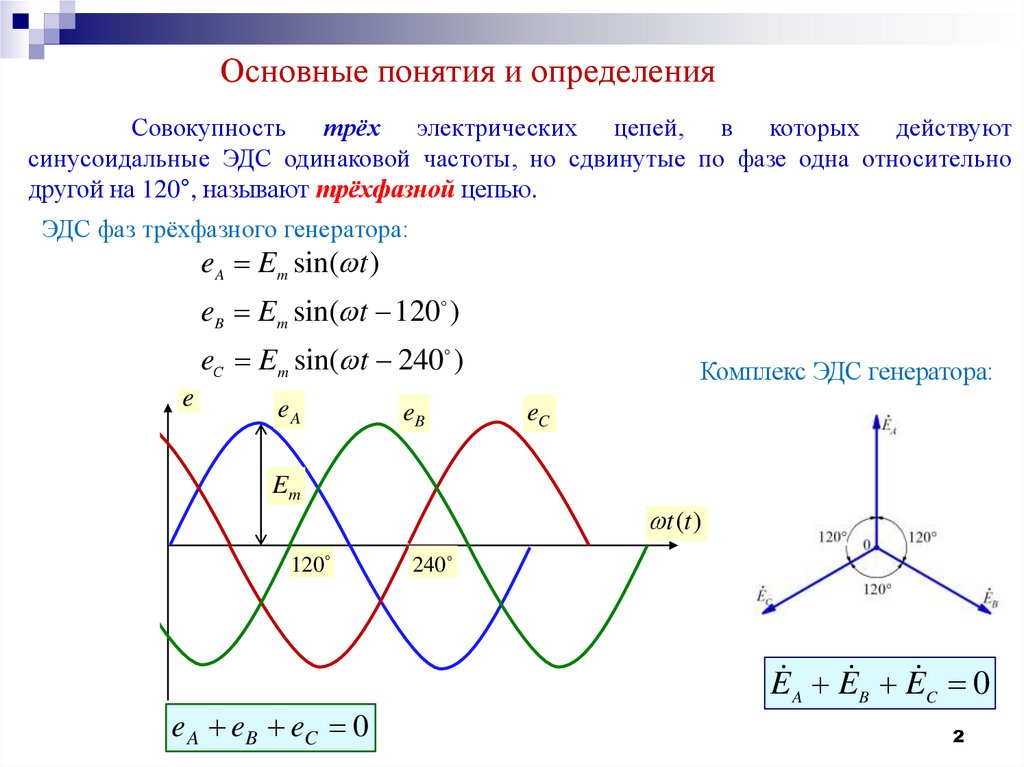
Основные понятия и определения
Совокупность трёх электрических цепей, в которых действуют
синусоидальные ЭДС одинаковой частоты, но сдвинутые по фазе одна относительно
другой на 120°, называют трёхфазной цепью.
ЭДС фаз трёхфазного генератора:
eA Em sin( t )
eB Em sin( t 120 )
eС Em sin( t 240 )
e
eA
eB
Em
120
e A eB eC 0
Комплекс ЭДС генератора:
eC
t (t )
240
E A E B E C 0
2

3.

Способы соединения источников ЭДС трёхфазного соединения
Существуют два основных способа соединения обмоток генератора и приёмника в
трехфазных цепях: звездой и треугольником.
A
A
uA
uC
eA
eC
N (0)
C
eB
eC
C
eA
B
eB
uB
Соединение источников
ЭДС звездой
B
Соединение источников ЭДС
треугольником
Концы фаз генератора (источников ЭДС) обозначают А,
В, С.
Соединенные вместе концы фаз генератора называется нейтральной (нулевой)
точкой N(0).

4.

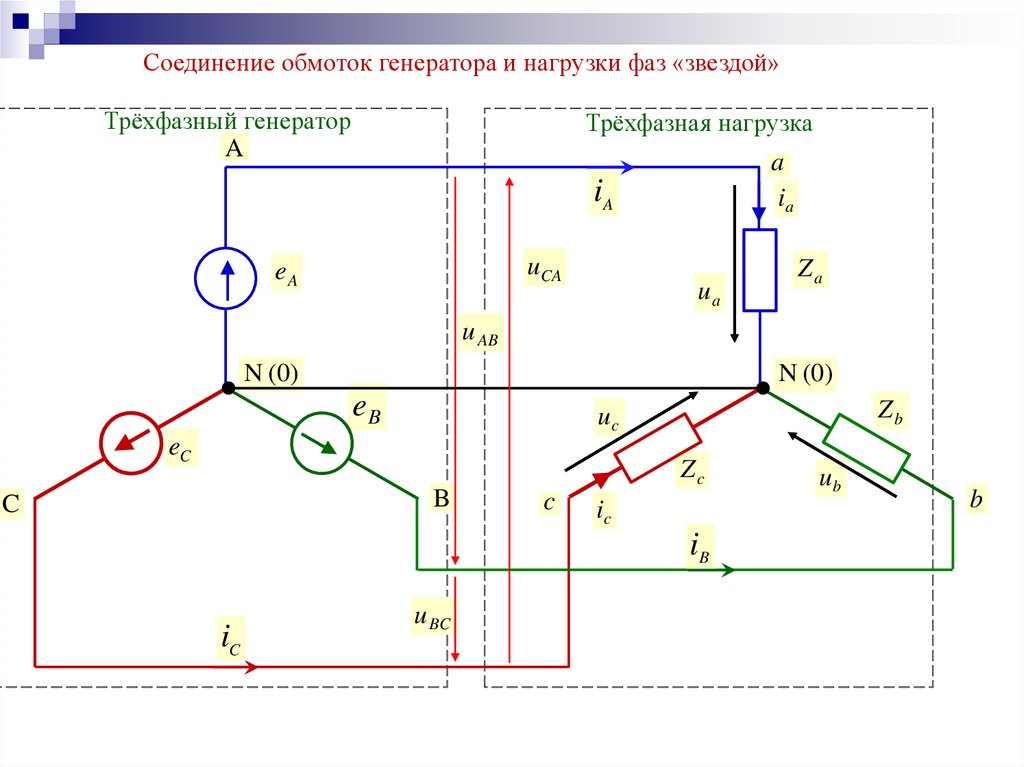
Соединение обмоток генератора и нагрузки фаз «звездой»
Трёхфазный генератор
A
Трёхфазная нагрузка
a
ia
iA
uCA
eA
ua
Za
u AB
N (0)
N (0)
eB
Zb
uc
eC
Zc
B
C
c
ic
iB
iC
u BC
ub
b

5.

Векторная диаграмма трёхфазного генератора соединенного звездой
A
Фазные ЭДС и комплексные напряжения:
j 0
UA U e
e A Em sin( t )
eB Em sin( t 120 )
j120
UB U e
eB Em sin( t 120 )
U C U e j120
Линейные напряжения определяются
параметрами ЭДС трёхфазного генератора:
U AB U A U B
U BC U B U C
U U U
CA
C
A
U A
U CA
U C
C
0
U AB
U B
U BC
Если действующие значения равны
UA = UB = UC = U,
тогда UAB = UBC = UCA = U· 3
В России фазные напряжения
UA = UB = UC = U=220 В, следовательно
линейные напряжения UAB = UBC = UCA = U· 3 = 380 В
При составлении однолинейных электрических схем фазы вместо
А,В,С обозначают L1, L2, L3.
B

6.

Четырёхпроводное соединение
4 провода:
линейный провод А-а
линейный провод B-b
линейный провод C-c
нулевой провод 0-0’
ia
ib
ic
Для потребителей линейные напряжения остаются
неизменными и их значения определяются напряжениями на
зажимах трёхфазного источника:
U AB U A U B
U BC U B U C
U U U
CA
C
A
I a I b I c I N
линейные токи: iА, iB , iC
фазные токи: ia, ib , ic
В комплексной форме:
I , I , I и I , I , I
A
B
C
a
b
I A I a ;
I B I b ;
Если считать сопротивление линейных проводов I I
C
c
нулевым, тогда U U ;
U A Ua;
A
a
U B Ub;
U U ;
При соединении фаз нагрузки звездой
линейные токи равны фазным токам:
B
b
U C U c
UC Uc
c

7.

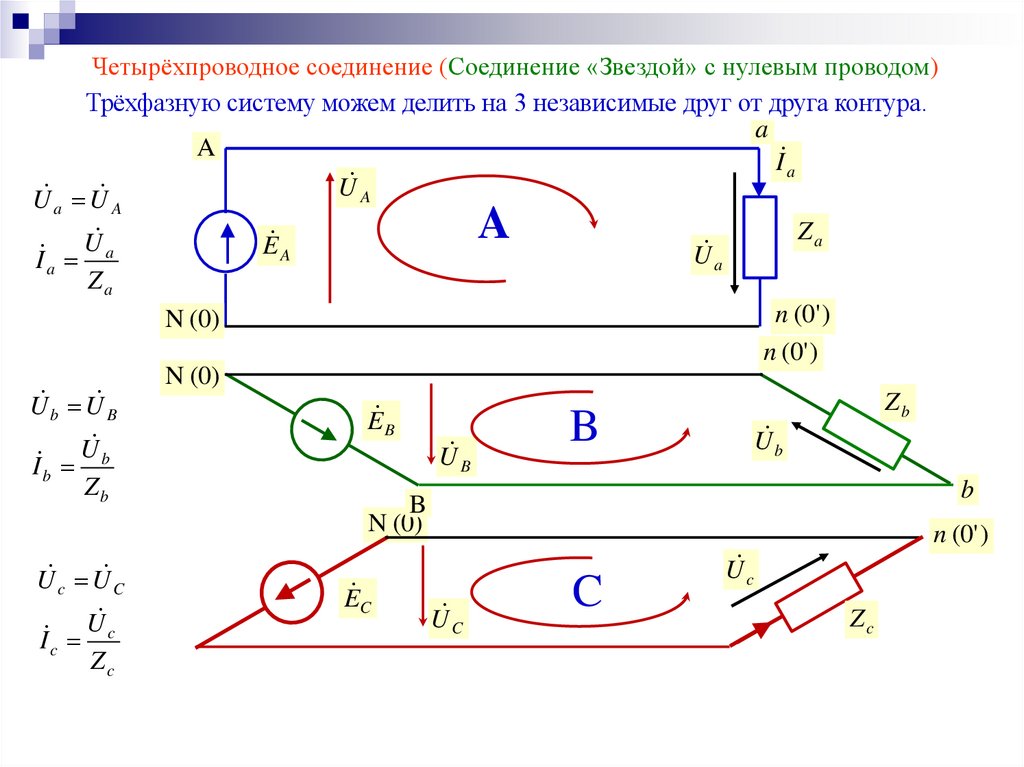
Четырёхпроводное соединение (Соединение «Звездой» с нулевым проводом)
Трёхфазную систему можем делить на 3 независимые друг от друга контура.
a
A
I a
U A
U a U A
Za
U
E
a
A
Ua
I a
Za
n (0' )
N (0)
n (0' )
N (0)
Zb
U b U B
E B
U b
U
UB
I b b
Zb
b
B
N (0)
n (0' )
A
B
U c U C
I U c
c
Zc
E C
U C
C
U c
Zc

8.

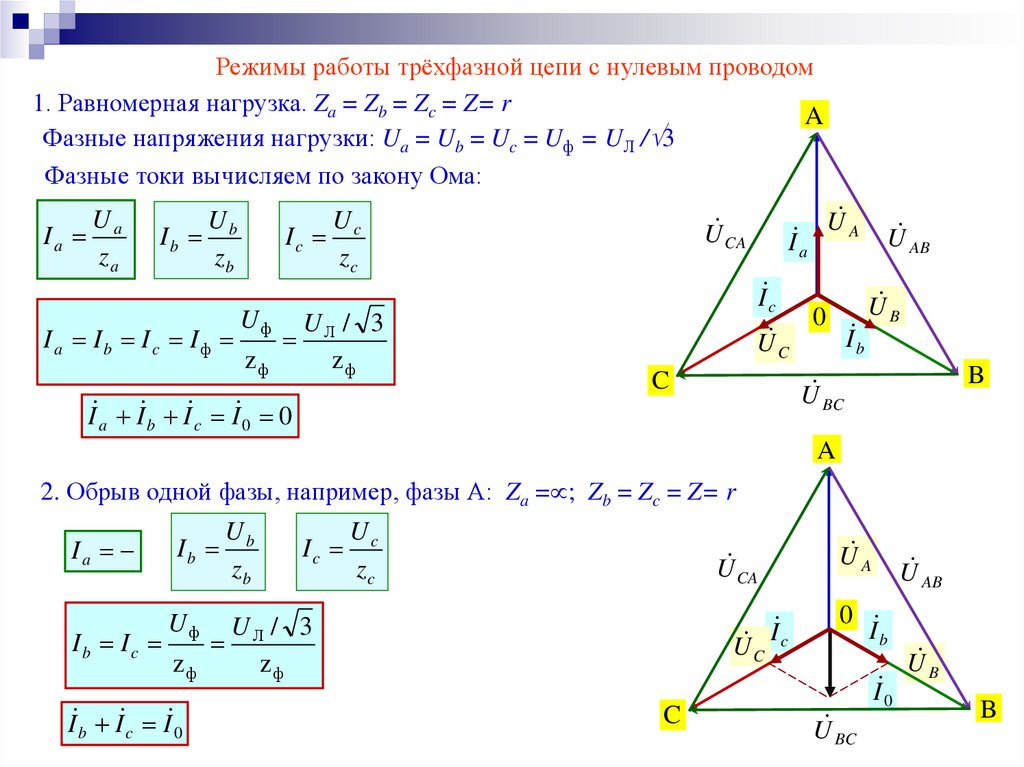
Режимы работы трёхфазной цепи с нулевым проводом
1. Равномерная нагрузка. Za = Zb = Zc = Z= r
A
Фазные напряжения нагрузки: Ua = Ub = Uc = Uф = UЛ / 3
Фазные токи вычисляем по закону Ома:
U
Ia a
za
U
Ib b
zb
I a Ib Ic Iф
U
Ic c
zc
Uф
zф
UЛ / 3
zф
U CA
U A
I a
I c
U
0
I b
C
C
U AB
U B
B
U BC
I a I b I c I 0 0
A
2. Обрыв одной фазы, например, фазы А: Za = ; Zb = Zc = Z= r
Ia
Ib
Ub
zb
Ic
Uc
zc
U CA
I
U C c
Uф
U / 3
Ib Ic
Л
zф
zф
I b I c I 0
C
U A
U AB
0
Ib
I 0
U BC
U B
B

9.

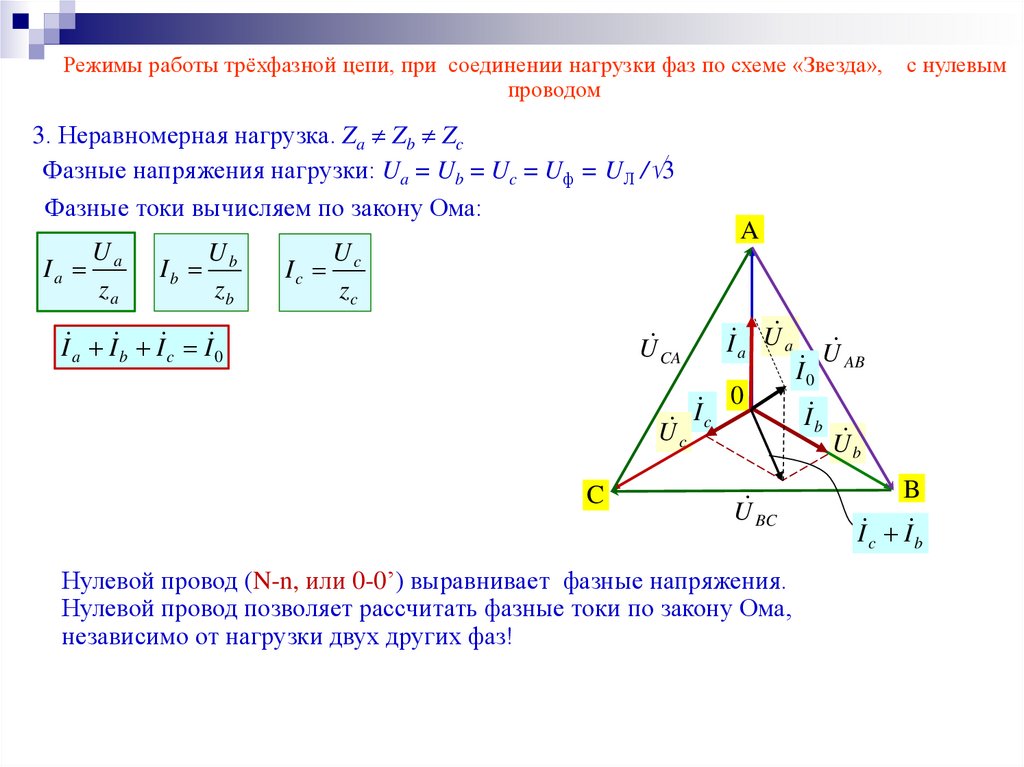
Режимы работы трёхфазной цепи, при соединении нагрузки фаз по схеме «Звезда»,
проводом
3. Неравномерная нагрузка. Za Zb Zc
Фазные напряжения нагрузки: Ua = Ub = Uc = Uф = UЛ / 3
Фазные токи вычисляем по закону Ома:
U
Ia a
za
U
Ib b
zb
U
Ic c
zc
I a I b I c I 0
U CA
A
I a U a
0
I
c
U c
C
с нулевым
U BC
Нулевой провод (N-n, или 0-0’) выравнивает фазные напряжения.
Нулевой провод позволяет рассчитать фазные токи по закону Ома,
независимо от нагрузки двух других фаз!
I U AB
0
I b
U b
B
I c I b

10.

Работа трёхфазной цепи без нулевого провода при соединении нагрузки фаз звездой
Пр
Za
I A a
Напряжение между нейтральными точками
А
фаз генератора и фаз приемника
Пр
Zb
U AYa U BYb U C Yc
I B b
U Nn
B
n
Ya Yb Yc
Пр
Zc
I C c
C
Y , Y , Y – проводимости фаз приемника
a
Схема соединения фаз приемника
без нулевого провода
b
c
1
Ya
Za
1
Yb
Zb
Yc
1
Zc
Алгебраическая сумма мгновенных значений фазных напряжений генератора равна нулю.
Сумма комплексов фазных напряжений генератора равна нулю.
U A U B U C 0

11.

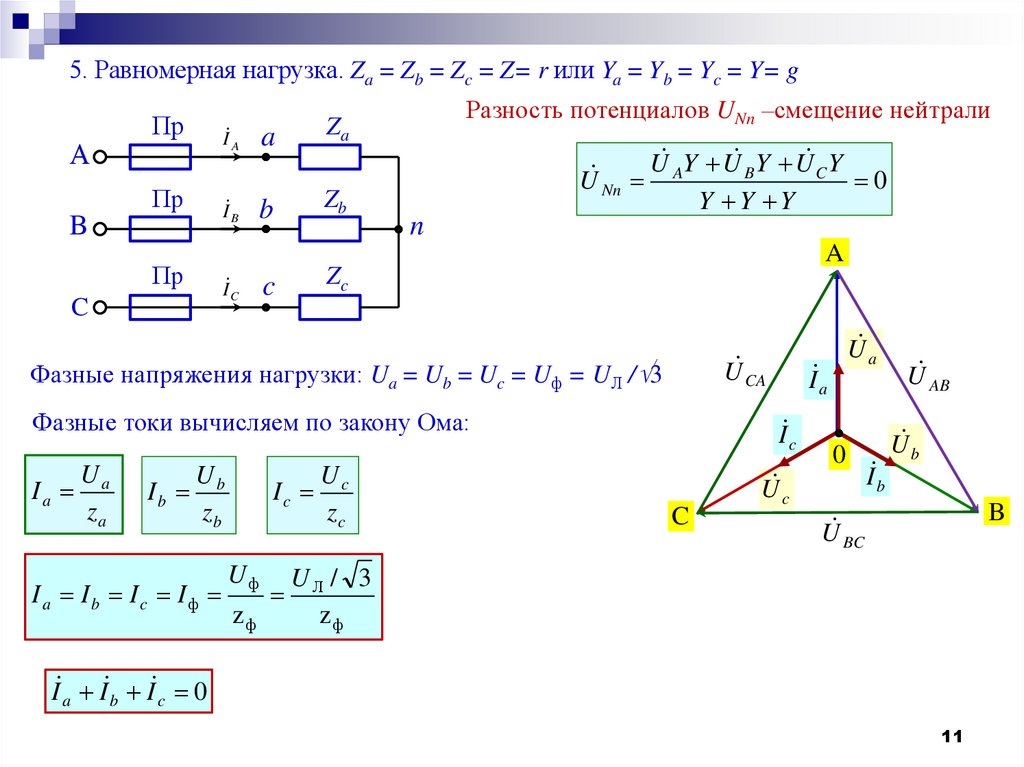
5. Равномерная нагрузка. Za = Zb = Zc = Z= r или Ya = Yb = Yc = Y= g
А
Пр
Пр
B
Пр
C
I A
a
Za
I B
b
Zb
I C
c
Разность потенциалов UNn –смещение нейтрали
n
U AY U BY U C Y
U Nn
0
Y Y Y
A
Zc
U CA
Фазные напряжения нагрузки: Ua = Ub = Uc = Uф = UЛ / 3
Фазные токи вычисляем по закону Ома:
U
Ia a
za
U
Ib b
zb
I a Ib Ic Iф
U
Ic c
zc
Uф
zф
I a
I c
C
U a
0
U c
I b
U AB
U b
B
U BC
UЛ / 3
zф
I a I b I c 0
11

12.

6. Обрыв одной фазы А: Za = ; Zb = Zc = Z= r или Ya =0; Yb = Yc = Y= g
А
Пр
Пр
B
Пр
C
Za
I A
a
I B
b
Zb
I C
c
Zc
n
(U B U C )Y U A
U Nn
Y Y
2
A, a
U A
U CA
Ia
Ib
Uф
Ub
zb
Ic
U / 3
Ib Ic
Л
zф
zф
I b I c 0
Uc
zc
U AB
0
UNn
C, c
U C
I c
U BC
I b
B, b
U B

13.

8. Короткое замыкание одной фазы без нулевого провода, например, фазы А:
Za = ; Zb = Zc = r
I a ( I b I c )
Внимание! Короткое замыкание при наличии нулевого провода,
является аварийным режимом!
Пр
А
a
A, a
Пр
b
В
Zb
I c
n
Пр
С
I C
c
U a I a Z a 0
U AB U a U b U b
U BC U b U c
U U U U
CA
Za=0
c
a
I a I b I c 0
c
Zc
I U b U AB
b
Zb
Zb
U CA
U c U CA
C, c
U c
U BC
n
U a 0
I b
U b U AB
U a
N
U b
Nn
B, b
I U c U CA
c
Zc
Zc
I a ( I b I c )
13

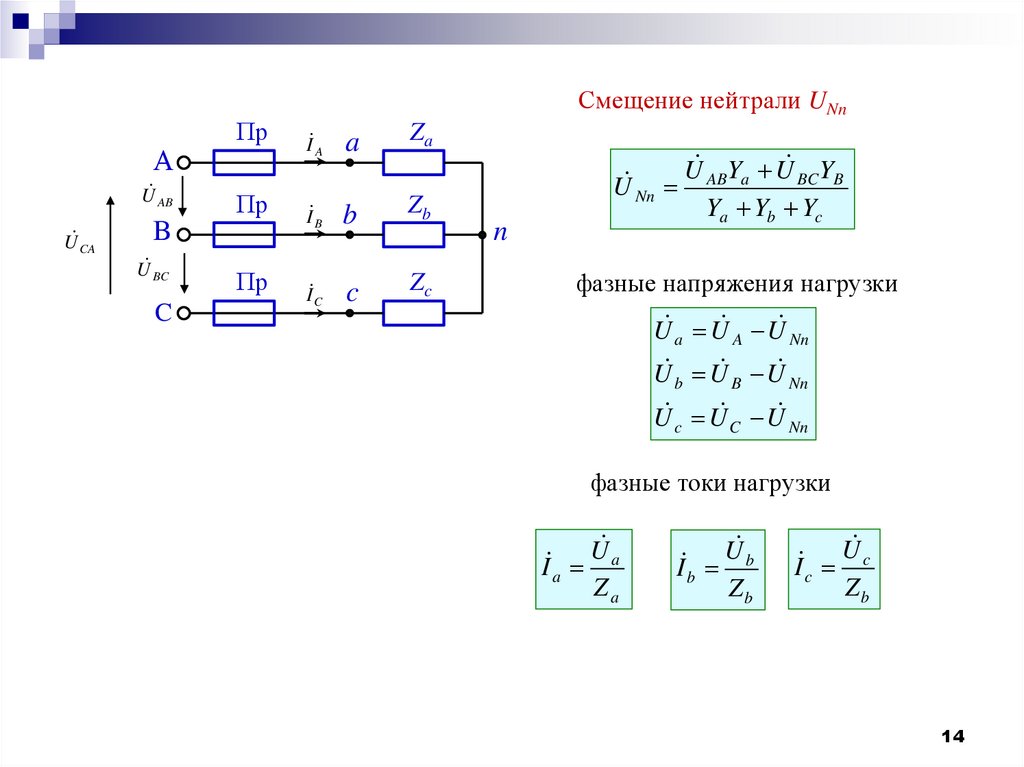
14.

А
U AB
U CA
Пр
Пр
B
U BC
C
Пр
Смещение нейтрали UNn
I A
a
Za
I B
b
Zb
I C
c
Zc
n
U ABYa U BC YB
U Nn
Ya Yb Yc
фазные напряжения нагрузки
U a U A U Nn
U b U B U Nn
U U U
c
C
Nn
фазные токи нагрузки
I U a
a
Za
I U b
b
Zb
I U c
c
Zb
14

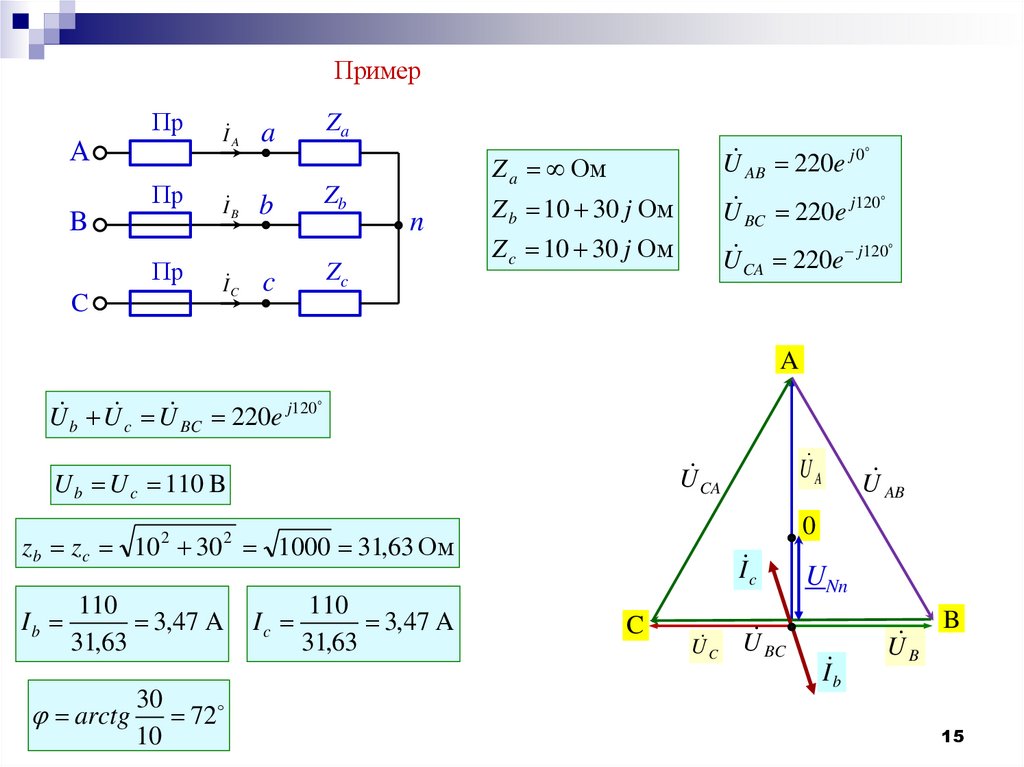
15.

Пример
А
Пр
Пр
B
Пр
C
I A
I B
I C
Za
a
Zb
b
n
Zc
c
Z a Ом
U AB 220e j 0
Z b 10 30 j Ом
U BC 220e j120
Z c 10 30 j Ом
j120
U CA 220e
A
U b U c U BC 220e j120
U b U c 110 B
Ib
2
110
3,47 A
31,63
arctg
30
72
10
Ic
110
3,47 A
31,63
U AB
0
zb zc 10 30 1000 31,63 Ом
2
U A
U CA
I c
C
U C
U BC
UNn
I b
U B
B
15