Функция y = x2

1. Функция y = x2

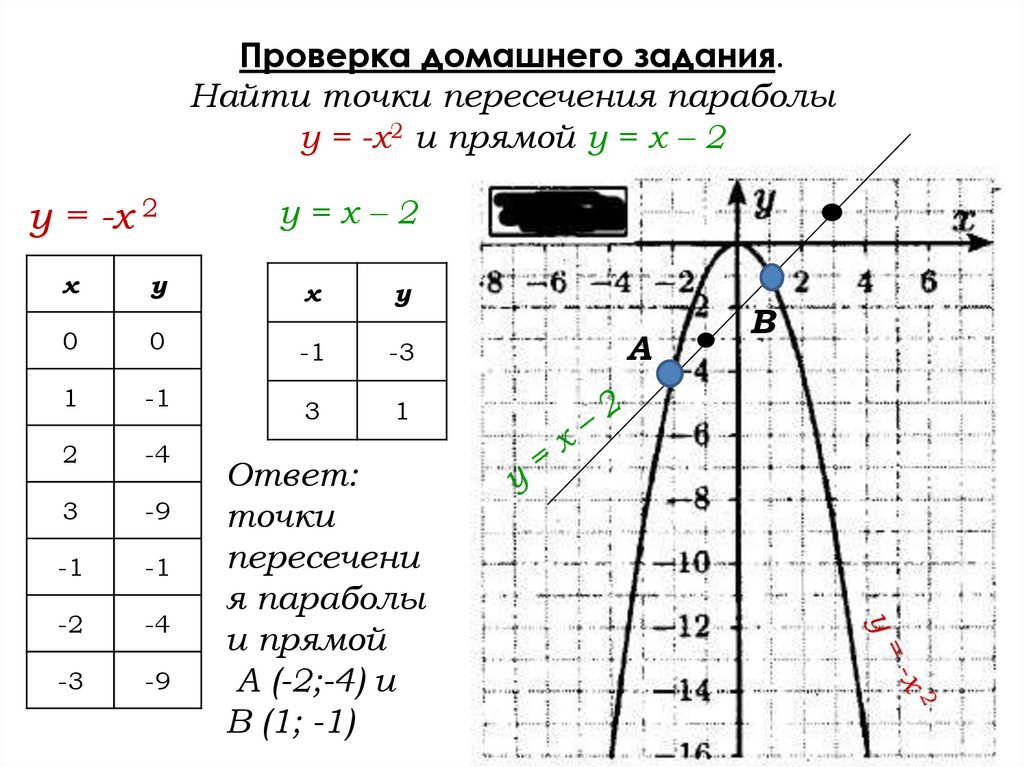
24.04.2020

2. Проверка домашнего задания:

Найти точки пересечения параболы у = -х2 и прямой
у = х - 2:
Алгоритм выполнения:
1. Составить таблицу для графика функции у = -х2 ,
отдельно составить таблицу для прямой у = х - 2.
2. Начертить координатную плоскость
3. Отметить на одной координатной плоскости
сначала точки для графика функции у = -х2 , и
соединить их последовательно, получив параболу.
4. На этой же координатной плоскости отметить
точки для прямой у = х - 2, через точки провести
прямую.
5. Подписать графики функций.
5. Отметить точки пересечения параболы и прямой
заглавными буквами.
6. Записать ответ.

3. Проверка домашнего задания. Найти точки пересечения параболы у = -х2 и прямой у = х – 2

y = -x 2
х
у
0
0
1
-1
2
-4
3
-9
-1
-1
-2
-4
-3
-9
у=х–2
х
у
-1
-3
3
1
Ответ:
точки
пересечени
я параболы
и прямой
А (-2;-4) и
В (1; -1)
А
В

4.

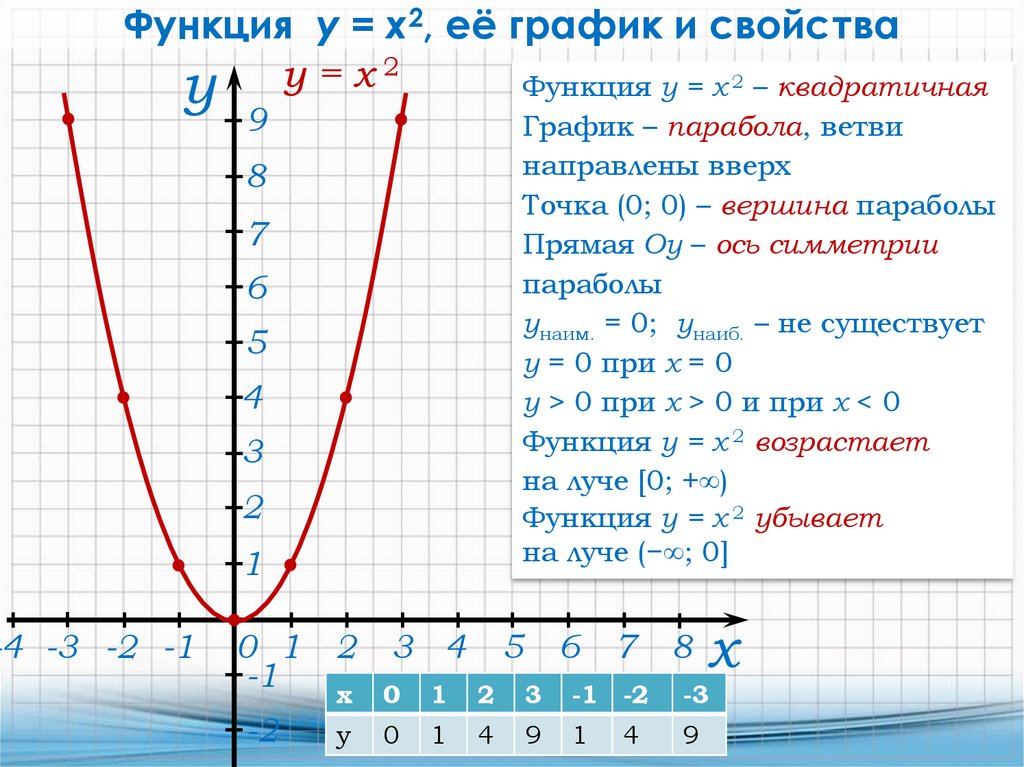
Функция y = x2, её график и свойства
2
y
=
x
Функция у = х 2 – квадратичная
у
-4 -3 -2 -1
9
График – парабола, ветви
направлены вверх
Точка (0; 0) – вершина параболы
Прямая Оу – ось симметрии
параболы
унаим. = 0; унаиб. – не существует
у = 0 при х = 0
у > 0 при х > 0 и при x < 0
Функция у = х 2 возрастает
на луче [0; +∞)
Функция у = х 2 убывает
на луче (−∞; 0]
8
7
6
5
4
3
2
1
0 1 2
-1
х
-2
у
3 4
5
6
7
8
х
0
1
2
3
-1 -2
-3
0
1
4
9
1
9
4

5.

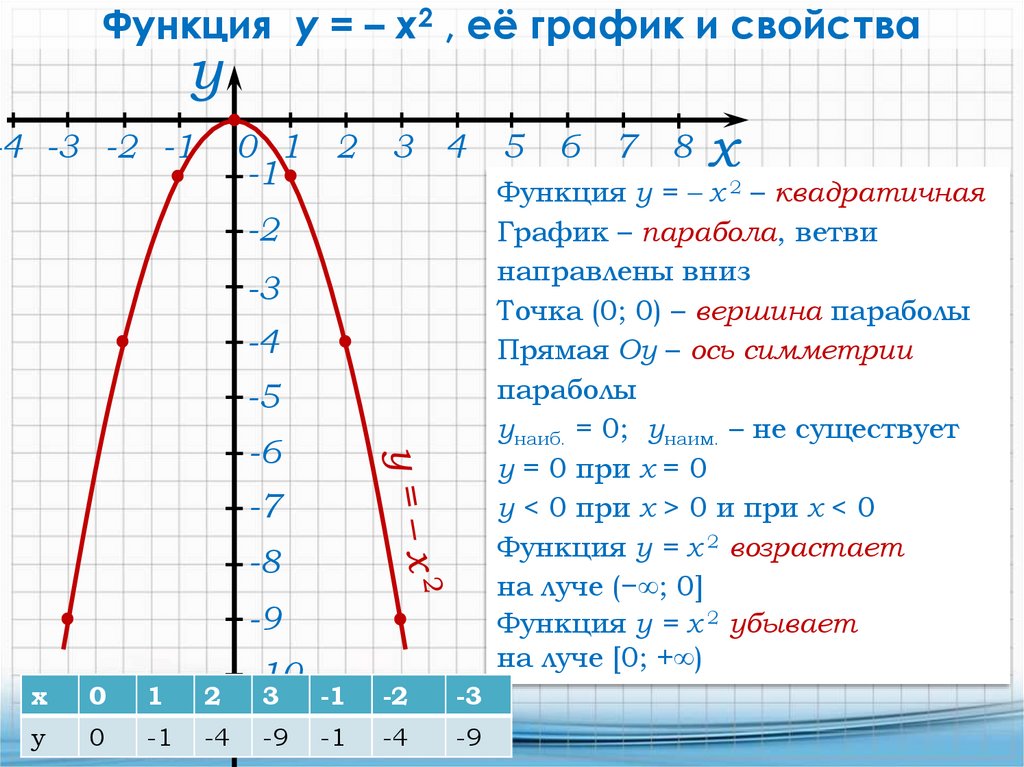
Функция y = – x2 , её график и свойства
у
-4 -3 -2 -1
0 1 2
-1
3 4
-3
-4
-5
-6
-7
-8
-9
0
1
2
у
0
-1
-4
-10
6
7
8
х
Функция у = – х 2 – квадратичная
График – парабола, ветви
направлены вниз
Точка (0; 0) – вершина параболы
Прямая Оу – ось симметрии
параболы
унаиб. = 0; унаим. – не существует
у = 0 при х = 0
у < 0 при х > 0 и при x < 0
Функция у = х 2 возрастает
на луче (−∞; 0]
Функция у = х 2 убывает
на луче [0; +∞)
-2
х
5
3
-1
-2
-3
-9
-1
-4
-9

6.

№ 37.28 (а) выполним графически
у
Строим график функция
у = х 2 , для этого нужно
составить таблицу:
9
8
7
6
4
3
А
-4 -3 -2 -1
1
В
0 1 2
-1
-2
0
1
2
3
-1 -2
-3
у
0
1
4
9
1
9
4
Строим график функция
у = 1, для этого таблица не
нужна, т.к. у нас уже есть
данные у=1, прямая будет
параллельна оси абсцисс (х).
5
2
х
y=1
3 4
5
6
7
8
х
Ответ: А ( -1;1) ; В ( 1;1).

7.

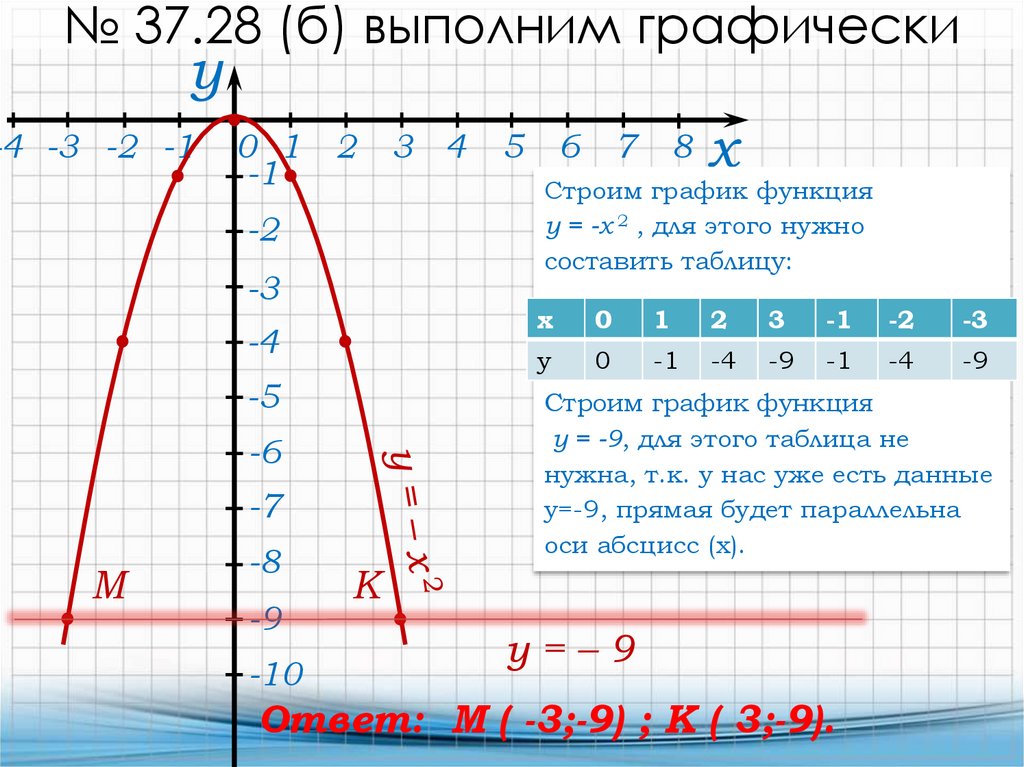
№ 37.28 (б) выполним графически
у
-4 -3 -2 -1
0 1 2
-1
-2
-3
-4
-5
-7
М
-9
-10
5
6
7
8
х
Строим график функция
у = -х 2 , для этого нужно
составить таблицу:
х
0
1
2
3
-1
-2
-3
у
0
-1
-4
-9
-1
-4
-9
Строим график функция
у = -9, для этого таблица не
нужна, т.к. у нас уже есть данные
у=-9, прямая будет параллельна
оси абсцисс (х).
-6
-8
3 4
К
y=–9
Ответ: М ( -3;-9) ; К ( 3;-9).

8.

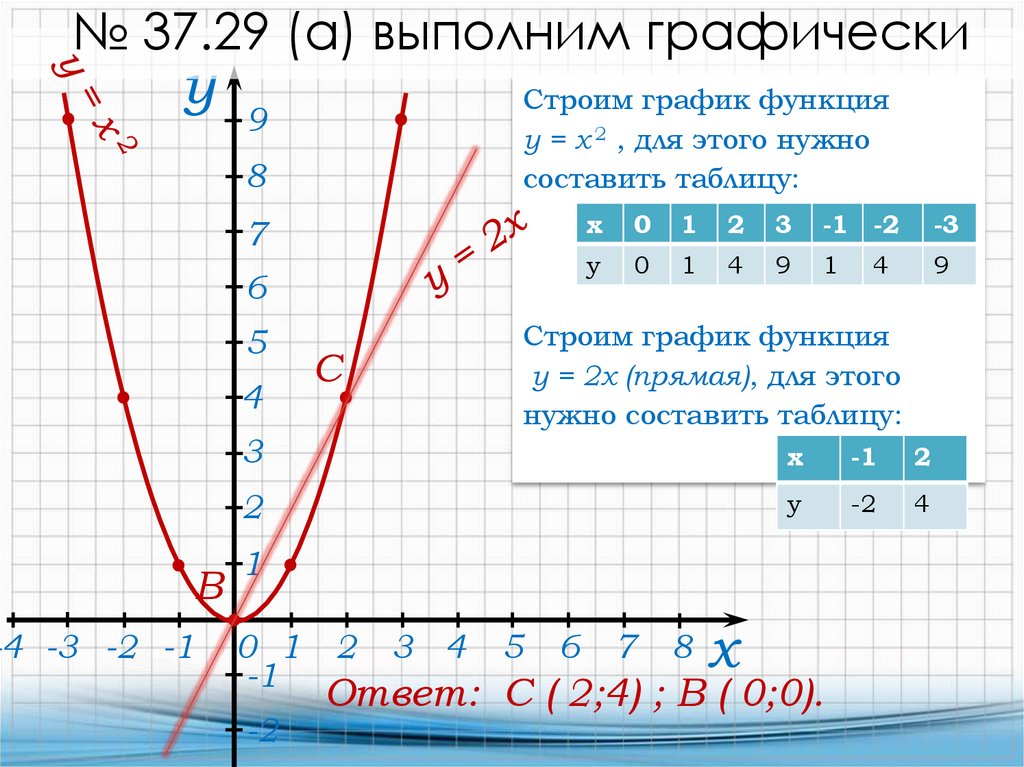
№ 37.29 (а) выполним графически
у
Строим график функция
у = х 2 , для этого нужно
составить таблицу:
9
8
7
6
5
4
х
0
1
2
3
-1 -2
-3
у
0
1
4
9
1
9
Строим график функция
у = 2х (прямая), для этого
нужно составить таблицу:
С
3
2
В
-4 -3 -2 -1
х
-1
2
у
-2
4
1
0 1 2
-1
-2
4
3 4
5
6
7
8
х
Ответ: С ( 2;4) ; В ( 0;0).

9.

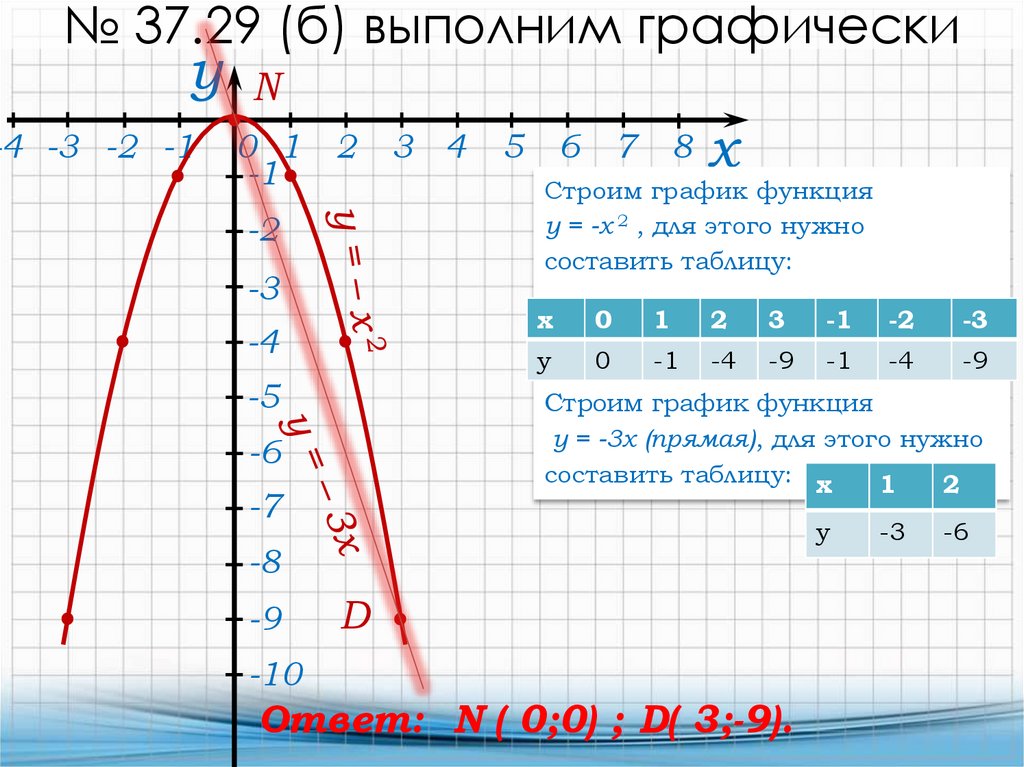
№ 37.29 (б) выполним графически
у
-4 -3 -2 -1
N
0 1 2
-1
-2
-3
-4
-5
3 4
5
6
7
8
х
Строим график функция
у = -х 2 , для этого нужно
составить таблицу:
х
0
1
2
3
-1
-2
-3
у
0
-1
-4
-9
-1
-4
-9
Строим график функция
у = -3х (прямая), для этого нужно
составить таблицу: х
1
2
-6
-7
у
-8
-9
D
-10
Ответ: N ( 0;0) ; D( 3;-9).
-3
-6

10.

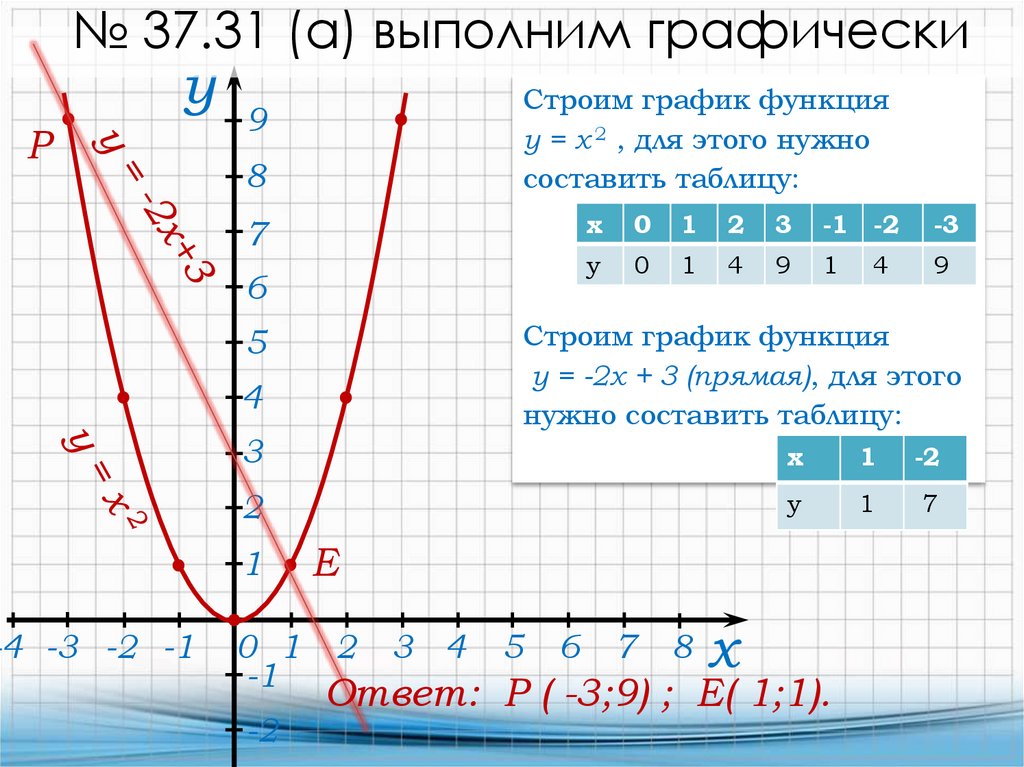
№ 37.31 (а) выполним графически
у
Р
-4 -3 -2 -1
Строим график функция
у = х 2 , для этого нужно
составить таблицу:
9
8
7
6
х
0
1
2
3
-1 -2
-3
у
0
1
4
9
1
9
Строим график функция
у = -2х + 3 (прямая), для этого
нужно составить таблицу:
5
4
3
2
1
х
1
-2
у
1
7
Е
0 1 2
-1
-2
4
3 4
5
6
7
8
х
Ответ: Р ( -3;9) ; Е( 1;1).

11.

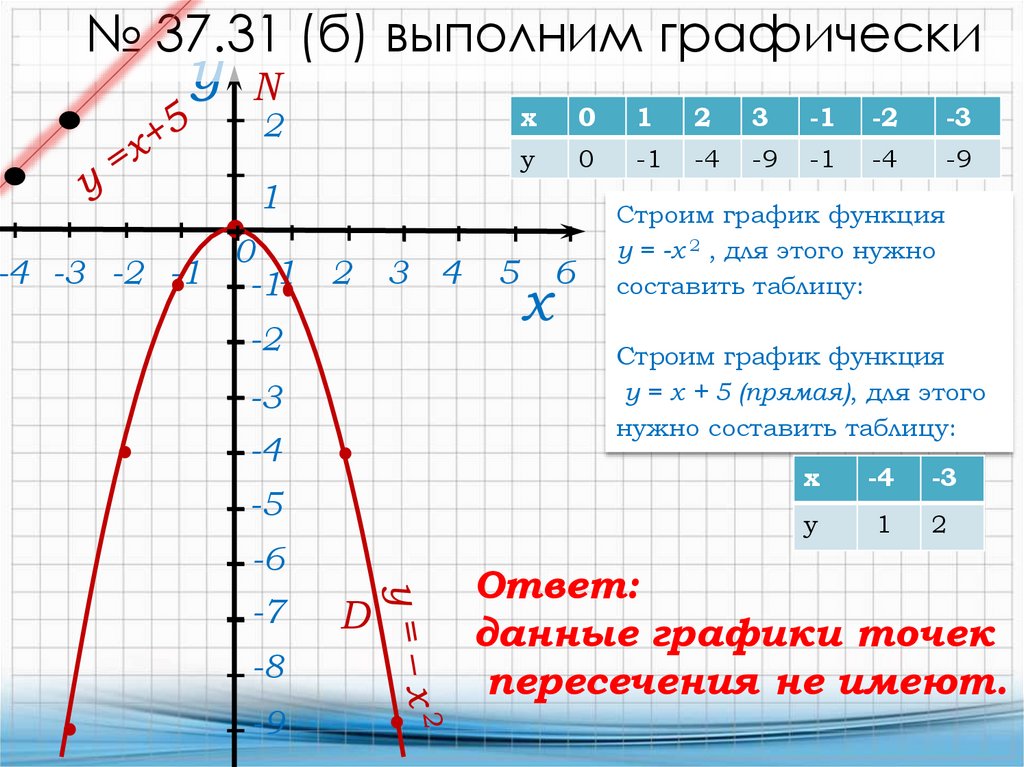
№ 37.31 (б) выполним графически
у
N
2
х
0
1
2
3
-1
-2
-3
у
0
-1
-4
-9
-1
-4
-9
1
0
-4 -3 -2 -1 -11 2
-2
-4
-5
-6
-8
-9
5
х
6
Строим график функция
у = х + 5 (прямая), для этого
нужно составить таблицу:
-3
-7
3 4
Строим график функция
у = -х 2 , для этого нужно
составить таблицу:
D
х
-4
-3
у
1
2
Ответ:
данные графики точек
пересечения не имеют.