Функция y = x2 и её график

1. Функция y = x2 и её график

Функция y =
и её график
2
x
Иванова Ю. Г.,
Учитель математики
МАОУ «Городская гимназия №1»

2. Цели урока:

• рассмотреть свойства и график функции
у = х2 ;
• научиться строить и «читать» график
данной функции;
• научиться решать уравнения
графическим способом.

3.

Назовите координаты точек, симметричных
данным точкам относительно оси y :
(- 2; 6)
(- 1; 4)
(0; 0)
(- 3; - 5)
y
( 2; 6)
(1; 4)
(0; 0)
(3; - 5)
х

4.

Найдите значение функции
y = 5x + 4, если:
х=-1
y=-1
y = 19
х=3
х=-2
y=-6
y = 29
х=5

5.

Укажите
область определения функции:
y = 16 – 5x
10
y
х
х – любое
число
х≠0
1
y
х 7
4х 1
y
5
х≠7

6.

Расшифруйте термины
Функция
Область
определения
Аргумент
Функция,
заданная
формулой
вида y независимая
= плоскости,
kx +при
b, где
Множество
Зависимость
Все значения,
всех
между
которые
точек
двумя
координатной
принимает
переменными,
которой
Независимая переменная, значения которой
абсциссы
хкаждому
переменная.
– переменная,
которых
значению
k иравны
bнезависимой
некоторые
значениям
числа,
переменной
аргумента,
её графиком
а
выбирают произвольно.
ординаты
соответствует
является
прямая.
– соответствующим
единственное значение
значениям
зависимой
функции.
переменной.
График функции
Линейная функция

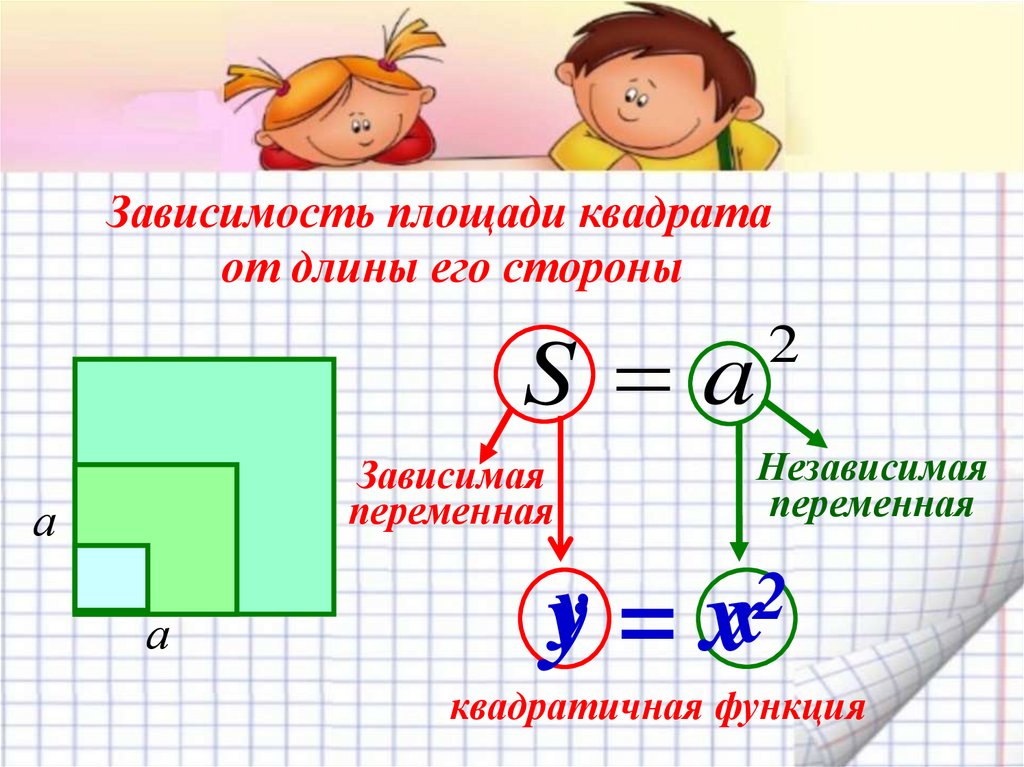
7. Зависимость площади квадрата от длины его стороны

S a
Зависимая
переменная
а
а
2
Независимая
переменная
2
y
y = xx
квадратичная функция

8.

Математическое
исследование
Функция y =
2
x

9.

Заполните таблицу значений функции y = x2:
х
y
- 3 - 2,5
- 2 - 1,5
- 1 - 0,5
0
9
6,25
4
2,25
1
0,25
0
х
y
0
0,5
1
1,5
2
2,5
3
0
0,25
1
2,25
4
6,25
9

10.

Постройте
график
функции y
= x2

11. Свойства функции y = x2

Свойства функции
y=
2
x

12.

• Область
определения
функции D(f):
х – любое число.
• Область значений
функции E(f):
все значения у ≥ 0.

13.

• Если х = 0, то у = 0.
График функции
проходит через
начало координат.

14.

II
I
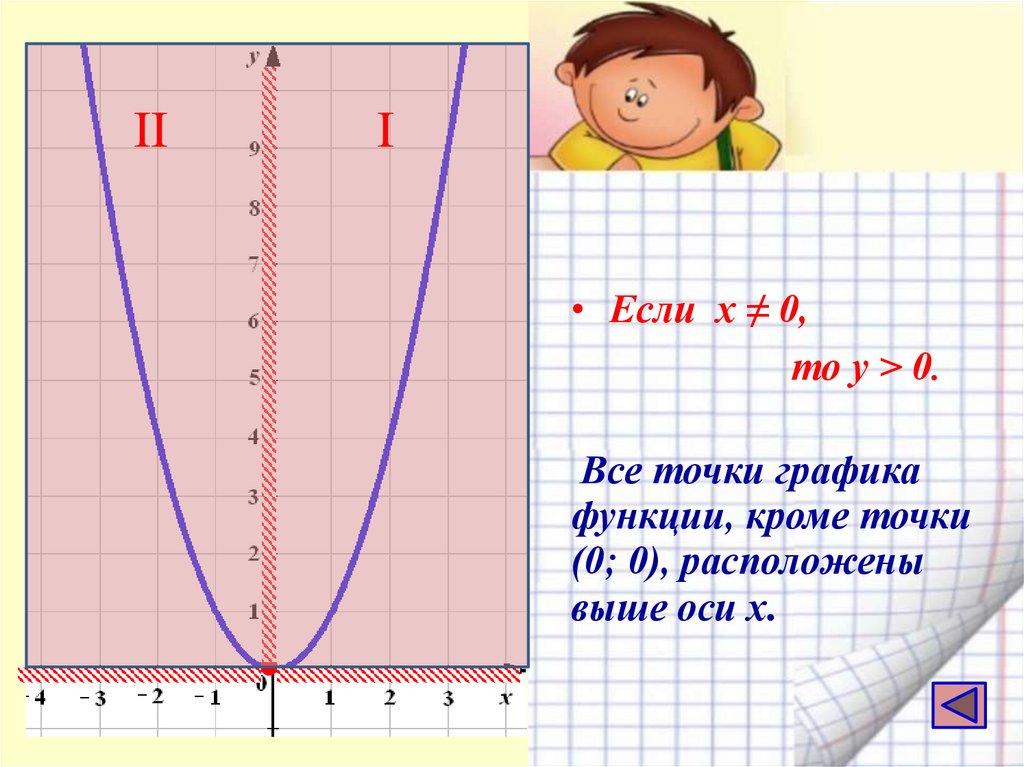
• Если х ≠ 0,
то у > 0.
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.

15.

• Противоположным
значениям х
соответствует одно
и то же значение у.
График функции
симметричен
относительно оси
ординат.
• Функция чётная.
(- х)2 = х2 при любом х

16.

Геометрические
свойства параболы
• Обладает симметрией
• Ось разрезает параболу
на две части: ветви
параболы
• Точка (0; 0) – вершина
параболы
• Парабола касается оси
абсцисс
Ось
симметрии

17.

Найдите у, если:
«Знание – орудие,
а не цель»
х = 1,4 - 1,4
у ≈ 1,9
х = - 2,6
у ≈ 6,7
х = 3,1 - 3,1
у ≈ 9,6
Найдите х, если:
Л. Н. Толстой
у=6
у=4
х ≈ 2,5 х ≈ -2,5
х=2
х=-2

18.

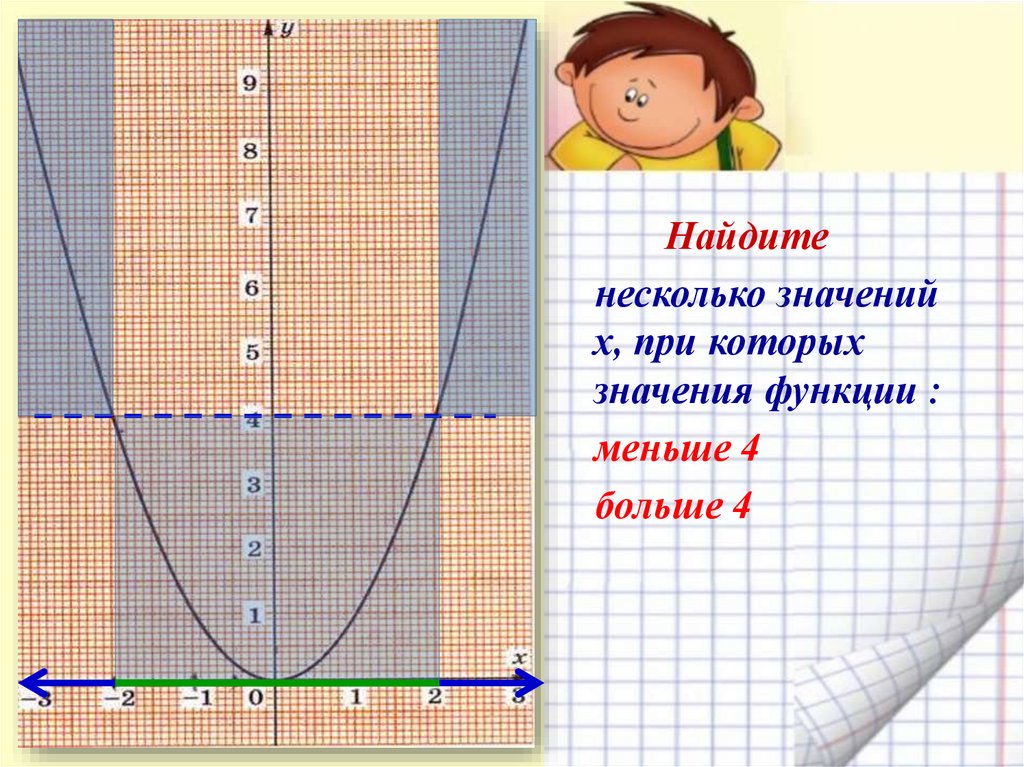
Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4

19.

• Принадлежит ли графику функции у = х2 точка:
P(-18; 324)
R(-99; -9081)
принадлежит
не принадлежит
S(17; 279)
не принадлежит
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2:
(-1; 1)
(-2; 4)
(0; 8)
(3; -9)
(1,8; 3,24)
(16; 0)
• При каких значениях а точка Р(а; 64) принадлежит
графику функции у = х2.
а = 8; а = - 8

20.

Удачи вам!