Пирамида и её элементы

1.

Математика уступает свои
крепости лишь сильным и
смелым.
(А.П. Конфорович)

2. МНОГОГРАННИКИ

ПИРАМИДА И ЕЁ ЭЛЕМЕНТЫ
Цель урока: рассмотреть еще один
многогранник – пирамиду, узнать
ее основные свойства.
Тип урока: уроки открытия нового
знания.
Метапредмет – Знак

3. Математическая разминка

1. Найдите объем параллелепипеда с длиной 8 см, шириной - 4
см и высотой – 3 см.
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

4. Ключевое слово урока

Форму пирамид имели гробницы фараонов в Древнем Египте.
Древнеегипетские пирамиды сохранились до наших дней. Одна
из самых знаменитых – пирамида Хеопса, высота которой
достигает 147 м. сооружения, похожие на египетские пирамиды,
строили и древние майя, жившие на американском континенте.
Их храмы имели форму усеченной пирамиды.
целеполагание

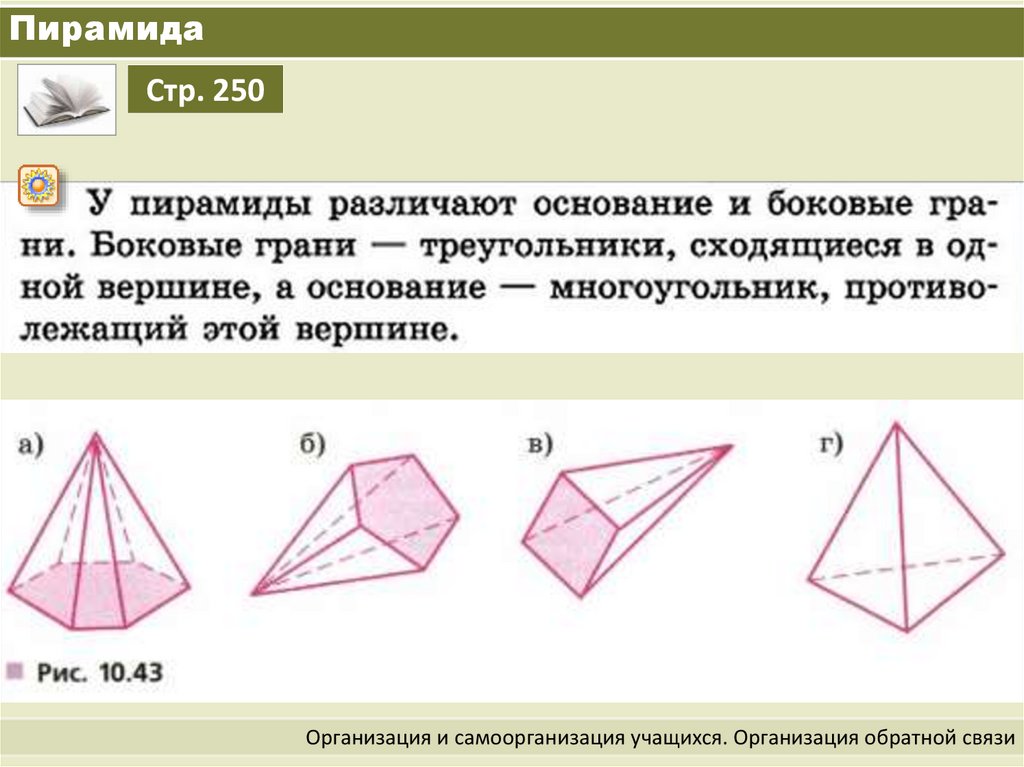
5. Пирамида

Стр. 250
Организация и самоорганизация учащихся. Организация обратной связи

6. Пирамида

Стр. 250
Организация и самоорганизация учащихся. Организация обратной связи

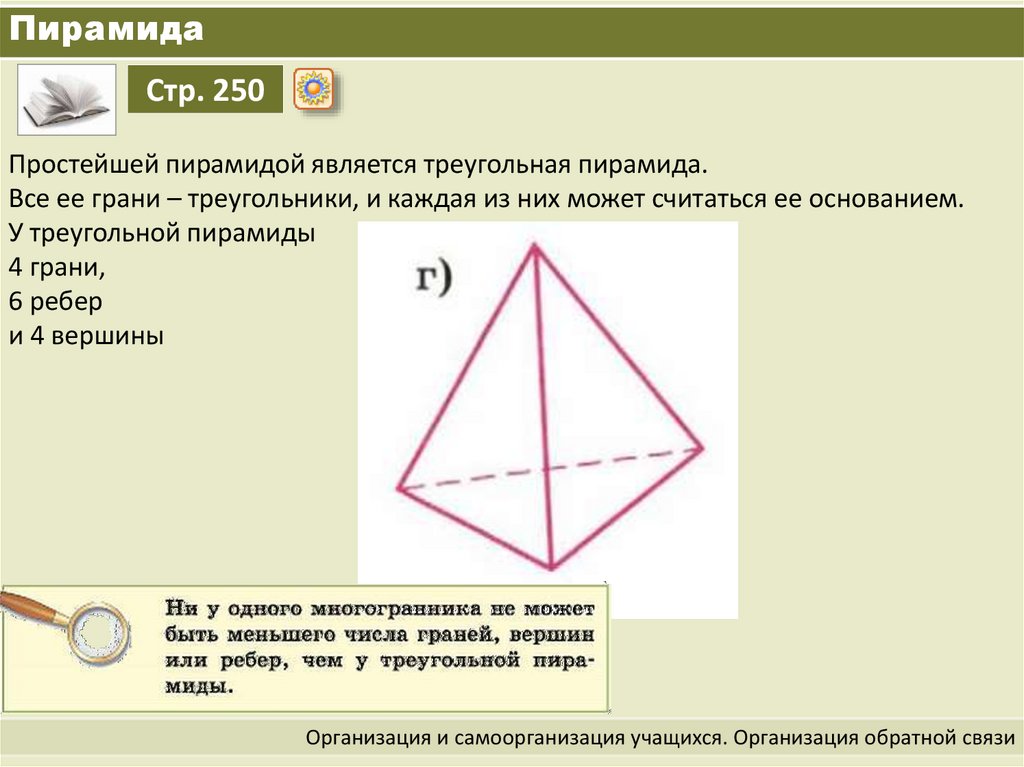
7. Пирамида

Стр. 250
Простейшей пирамидой является треугольная пирамида.
Все ее грани – треугольники, и каждая из них может считаться ее основанием.
У треугольной пирамиды
4 грани,
6 ребер
и 4 вершины
Организация и самоорганизация учащихся. Организация обратной связи

8. Изобразите пирамиду. Запишите ее обозначения

Название пирамиды начинается с буквы,
обозначающей её вершину, а потом буквы,
обозначающие основание, перечисленные по
часовой стрелке.
Пирамида MABCD.
M - вершина.
MA, MB, MC, MD – боковые
ребра.
MAB, MBC, MCD, MDA – боковые
грани.
ABCD - основание.
Организация и самоорганизация учащихся. Организация обратной связи

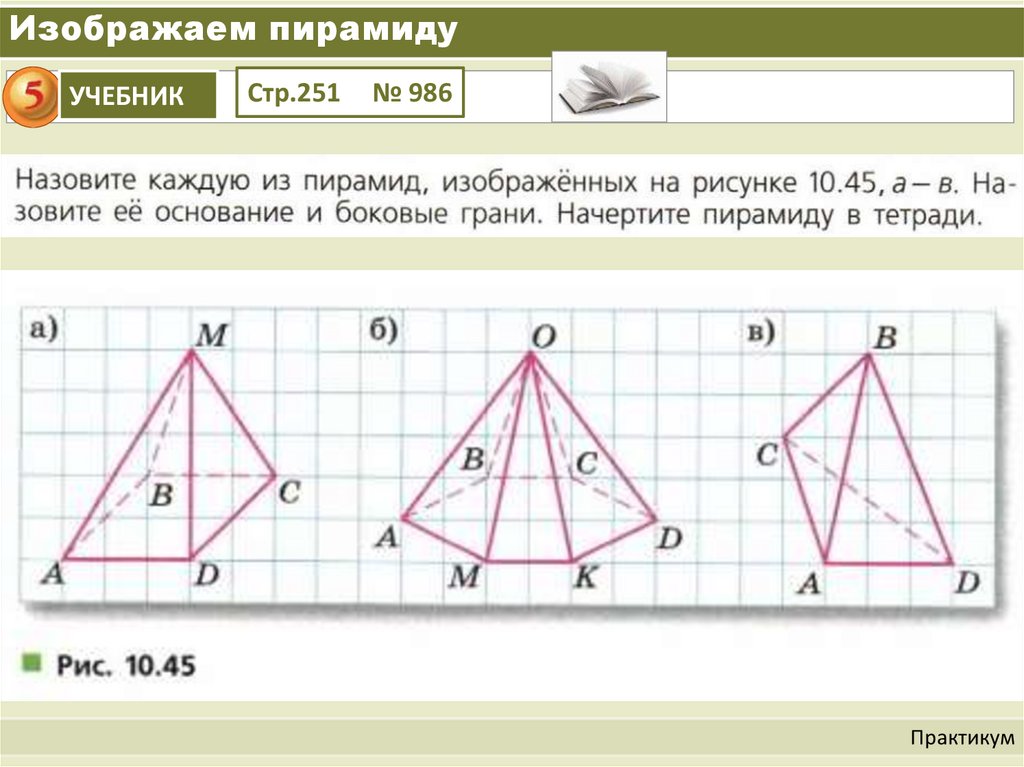
9. Изображаем пирамиду

УЧЕБНИК
Стр.251
№ 986
Практикум

10. Работаем с учебником

УЧЕБНИК
Стр.251
№ 987
5 ребер основания
5 боковых ребер
10 ребер всего
5 боковых граней
6 граней всего
6 вершин
Практикум

11. Работаем устно

УЧЕБНИК
Стр.252
№ 988
Практикум

12. Итог урока

Древнегреческий ученый Евклид говорил: «Это телесная фигура,
ограниченная плоскостями, которые от одной плоскости
(основания) сходятся к одной точке (вершине)».
Герон утверждал, что «Это фигура, ограниченная треугольниками,
сходящимися в одной точке, и основанием которой служит
многоугольник».
Английский математик Тейлор писал, что «Это многогранник, у
которого все грани, кроме одной,
сходятся в одной точке».
Что это за фигура?
Музей Лувр, Франция
Подведение итогов, рефлексия, домашнее задание.

13. Задание на дом

Домашнее задание
Учебник: тема 10.4 стр. 250 – 251 читать.
Письменно в тетрадях выполнить: № 987 (2);
№ 989.
Подведение итогов, рефлексия, домашнее задание.

14.

До свидания, ребята!
Спасибо за урок.
Хорошего Вам дня!
И успехов в учебе.