Similar presentations:
Пирамида. Элементы пирамиды
1.
Пирамида.2.
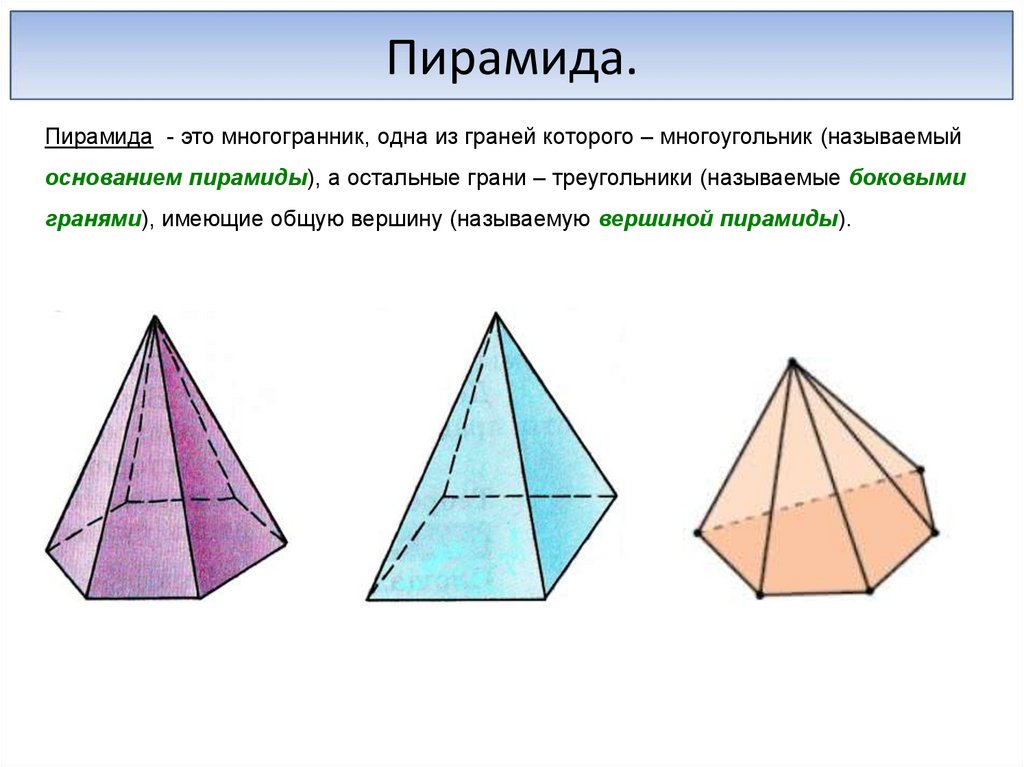
Пирамида.Пирамида - это многогранник, одна из граней которого – многоугольник (называемый
основанием пирамиды), а остальные грани – треугольники (называемые боковыми
гранями), имеющие общую вершину (называемую вершиной пирамиды).
3.
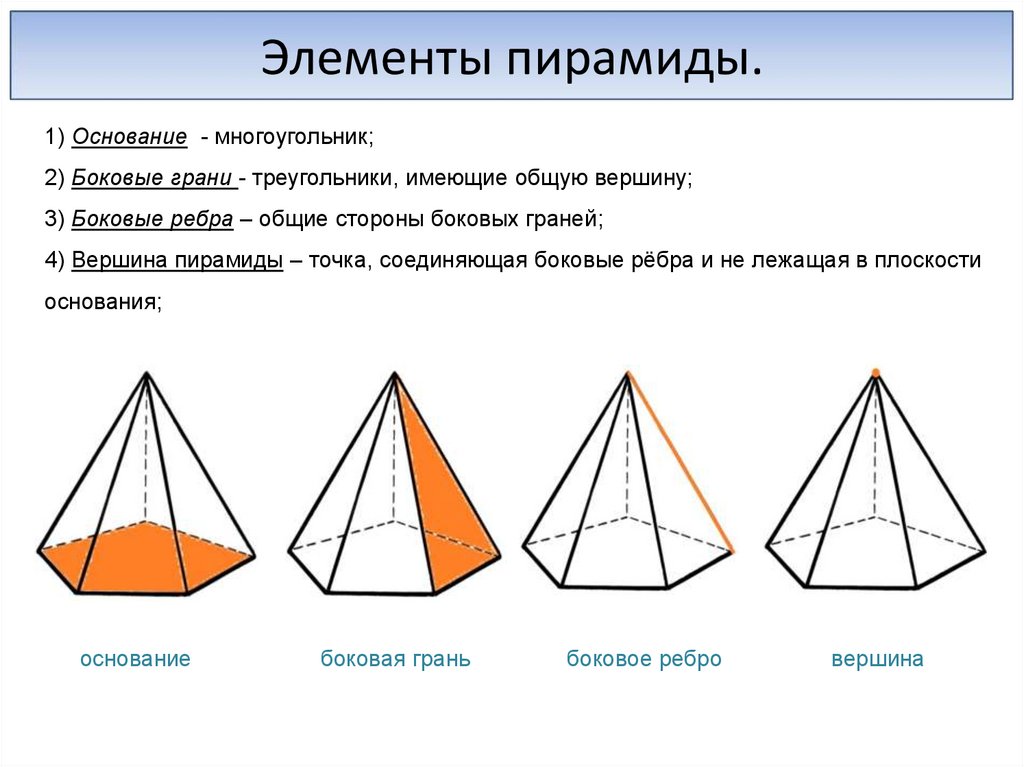
Элементы пирамиды.1) Основание - многоугольник;
2) Боковые грани - треугольники, имеющие общую вершину;
3) Боковые ребра – общие стороны боковых граней;
4) Вершина пирамиды – точка, соединяющая боковые рёбра и не лежащая в плоскости
основания;
основание
боковая грань
боковое ребро
вершина
4.
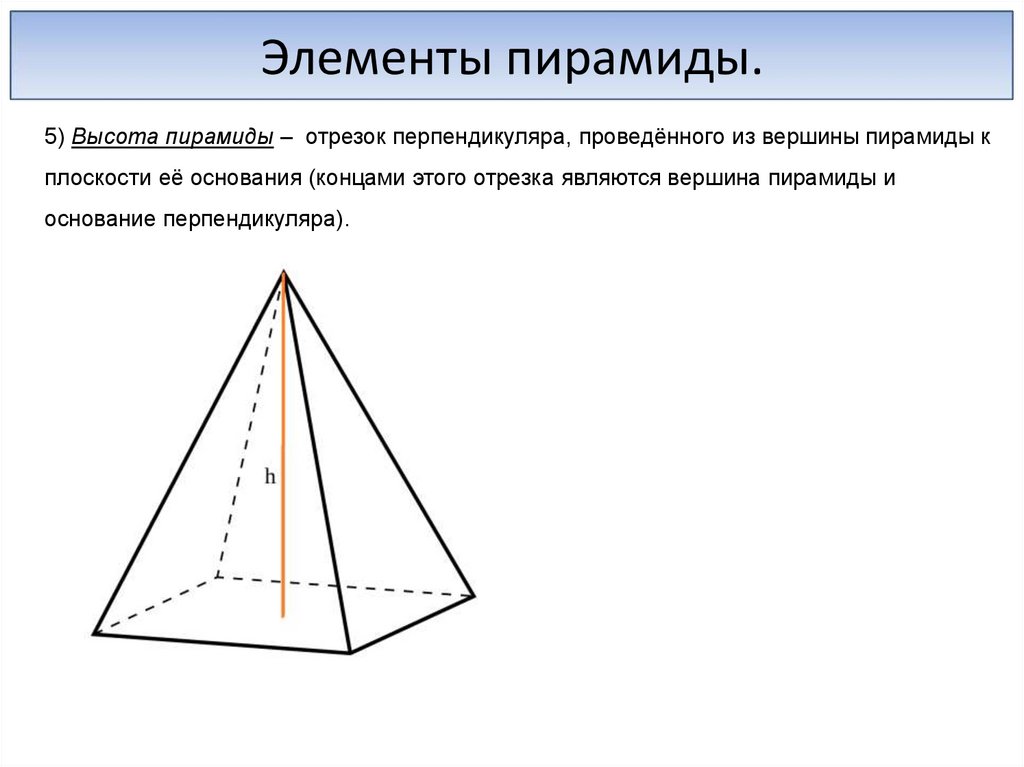
Элементы пирамиды.5) Высота пирамиды – отрезок перпендикуляра, проведённого из вершины пирамиды к
плоскости её основания (концами этого отрезка являются вершина пирамиды и
основание перпендикуляра).
5.
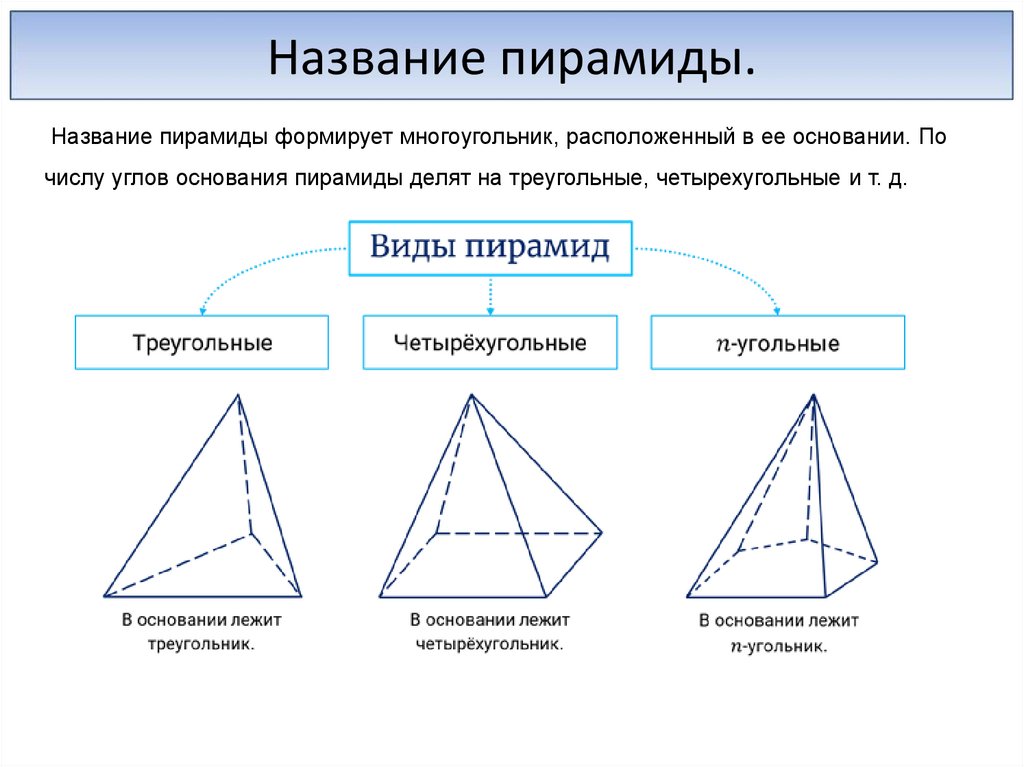
Название пирамиды.Название пирамиды формирует многоугольник, расположенный в ее основании. По
числу углов основания пирамиды делят на треугольные, четырехугольные и т. д.
6.
Особые случаи пирамид:1)
Прямоугольная пирамида – это пирамида, в которой одно из боковых рёбер
перпендикулярно основанию.
В этом случае, это ребро и будет высотой пирамиды.
h
7.
Особые случаи пирамид:2)
Наклонная пирамида – это пирамида, в которой основание высоты лежит за
пределами основания пирамиды.
h
8.
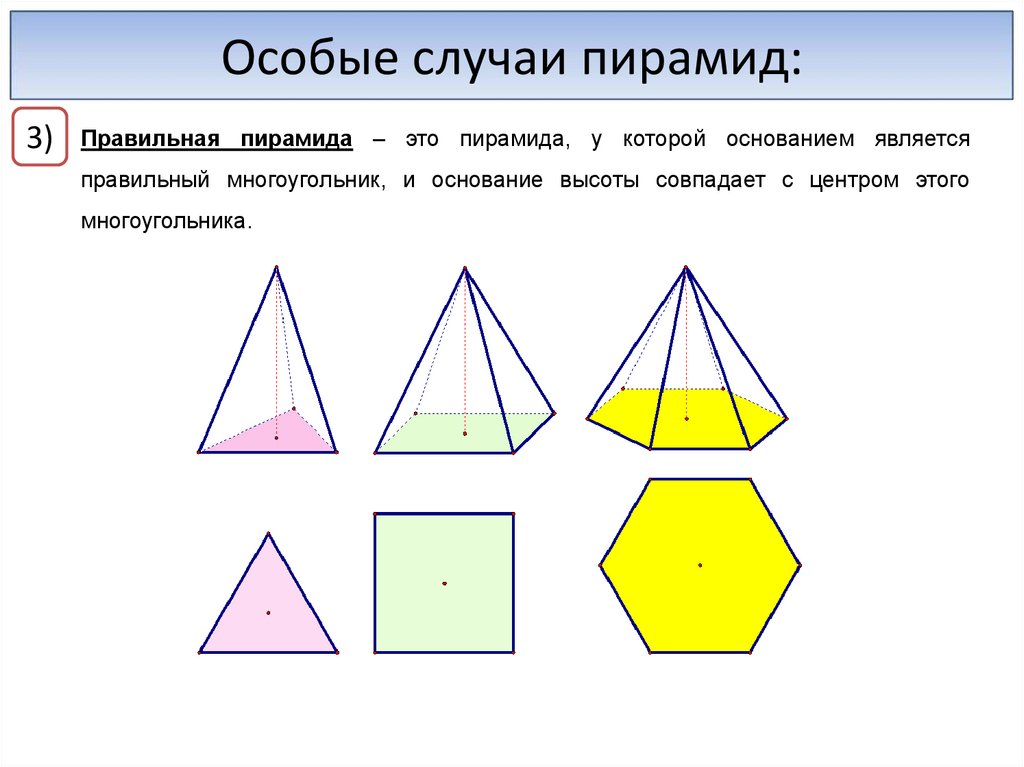
Особые случаи пирамид:3)
Правильная пирамида – это пирамида, у которой основанием является
правильный многоугольник, и основание высоты совпадает с центром этого
многоугольника.
9.
Свойства правильной пирамиды:1) Все боковые ребра правильной пирамиды равны;
2) Все боковые грани правильной пирамиды – это равные равнобедренные
треугольники;
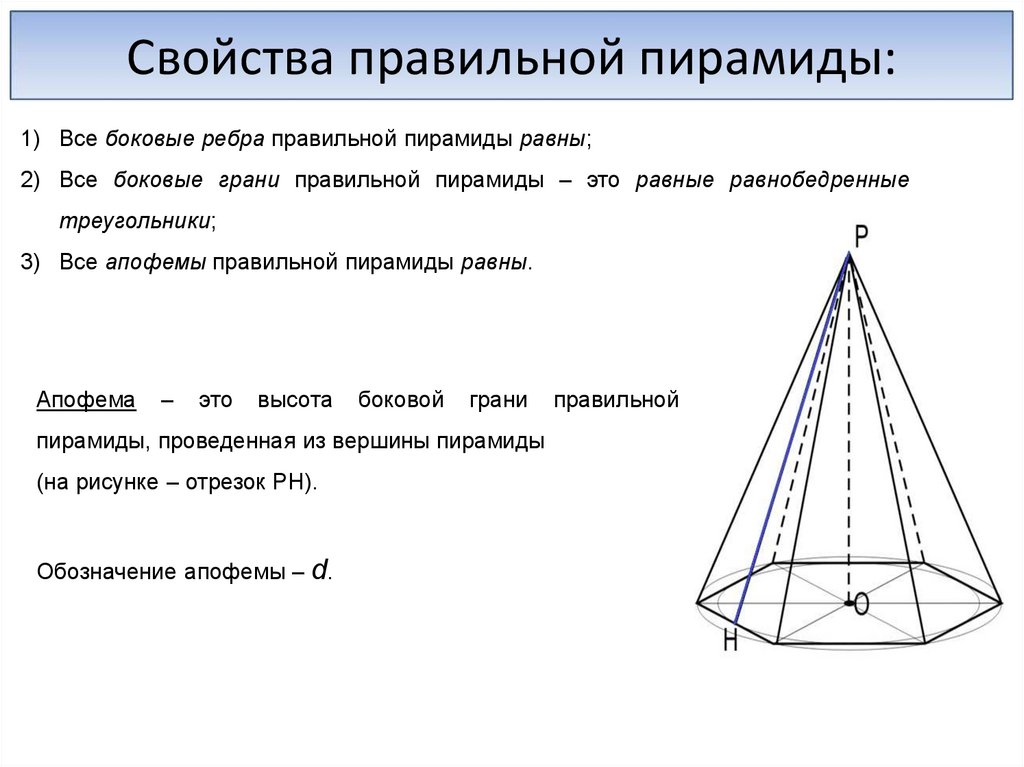
3) Все апофемы правильной пирамиды равны.
Апофема
–
это
высота
боковой
грани
пирамиды, проведенная из вершины пирамиды
(на рисунке – отрезок PH).
Обозначение апофемы – d.
правильной
10.
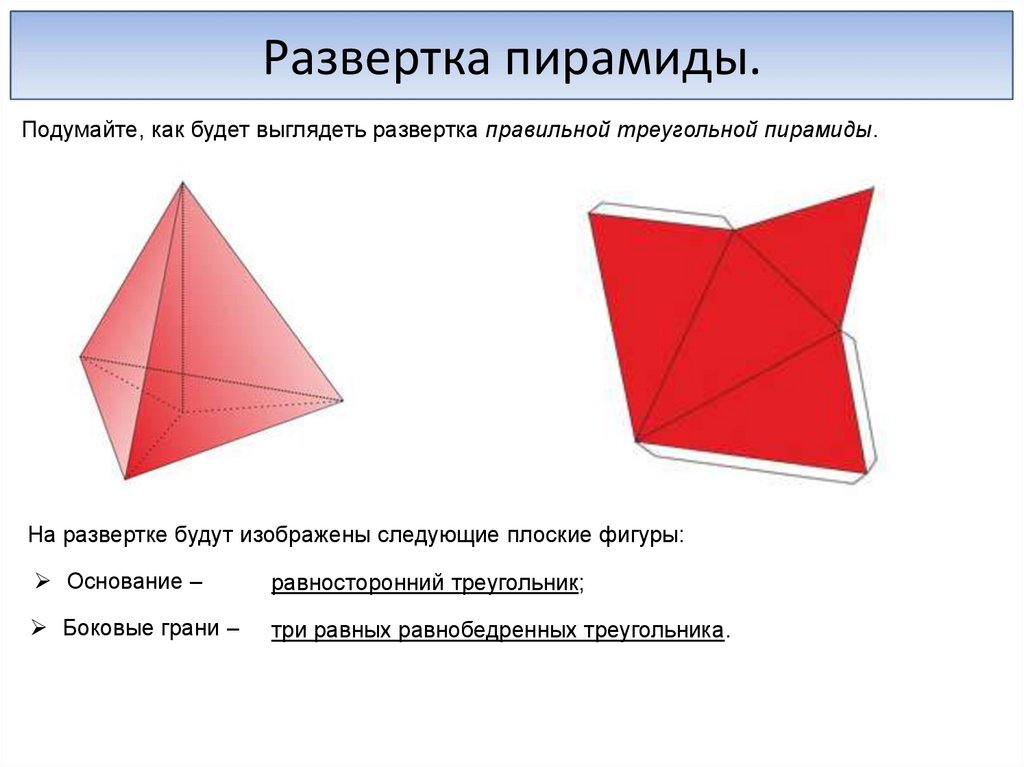
Развертка пирамиды.Подумайте, как будет выглядеть развертка правильной треугольной пирамиды.
На развертке будут изображены следующие плоские фигуры:
Основание –
равносторонний треугольник;
Боковые грани –
три равных равнобедренных треугольника.
11.
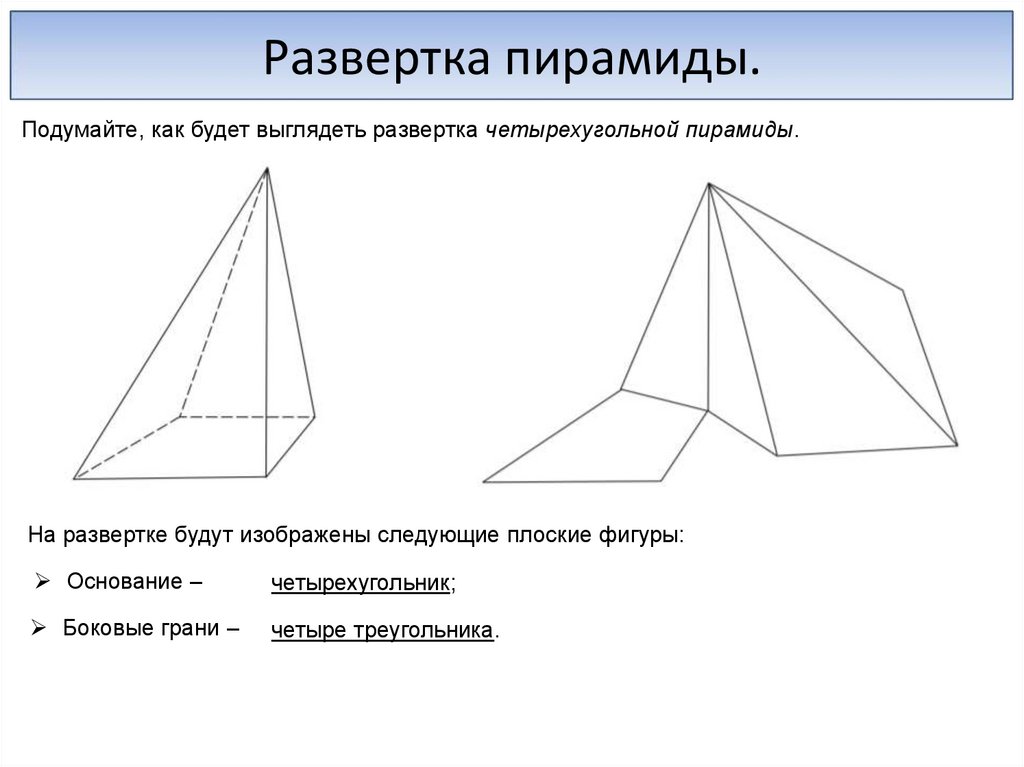
Развертка пирамиды.Подумайте, как будет выглядеть развертка четырехугольной пирамиды.
На развертке будут изображены следующие плоские фигуры:
Основание –
четырехугольник;
Боковые грани –
четыре треугольника.
12.
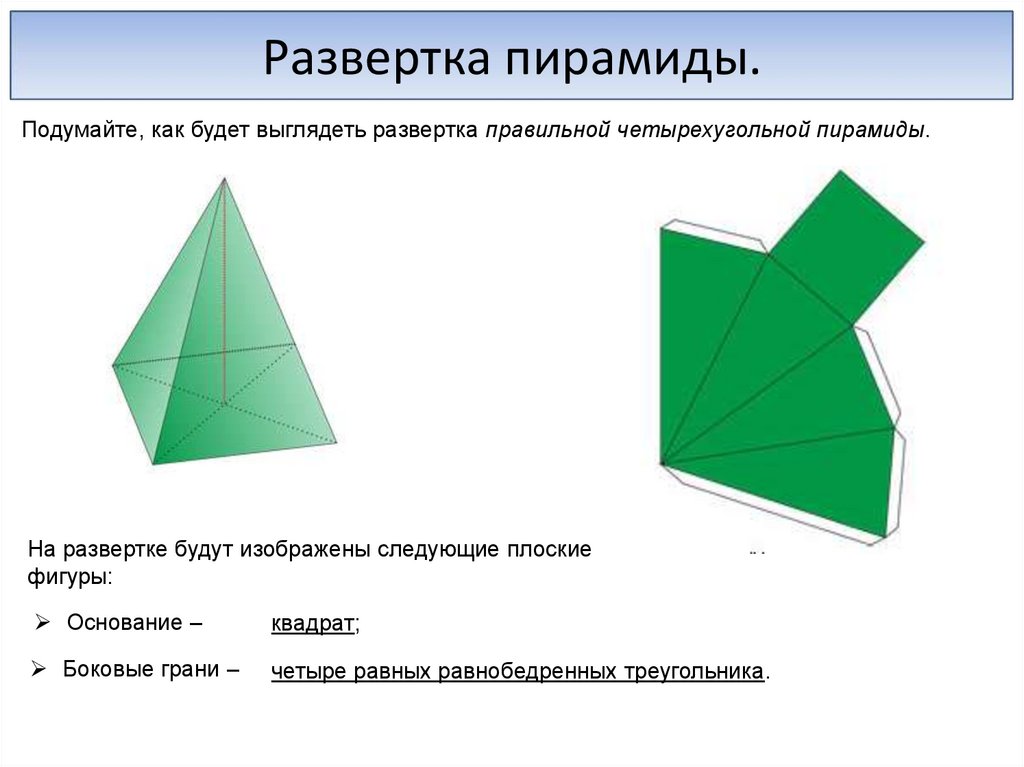
Развертка пирамиды.Подумайте, как будет выглядеть развертка правильной четырехугольной пирамиды.
На развертке будут изображены следующие плоские
фигуры:
Основание –
квадрат;
Боковые грани –
четыре равных равнобедренных треугольника.
13.
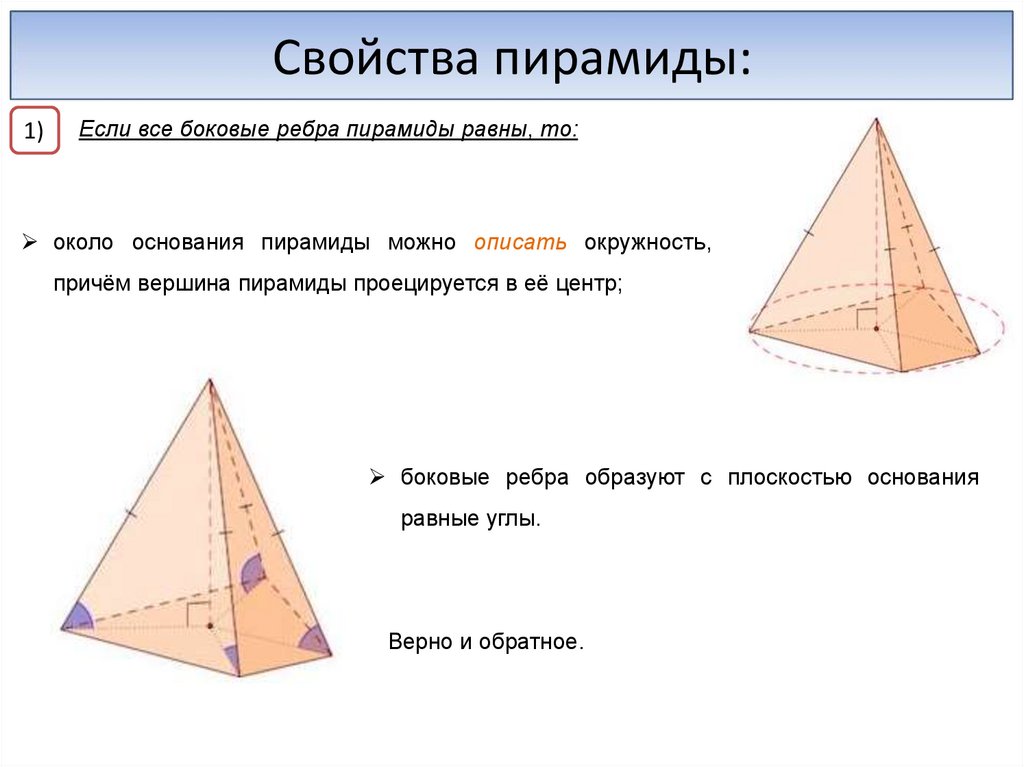
Свойства пирамиды:1)
Если все боковые ребра пирамиды равны, то:
около основания пирамиды можно описать окружность,
причём вершина пирамиды проецируется в её центр;
боковые ребра образуют с плоскостью основания
равные углы.
Верно и обратное.
14.
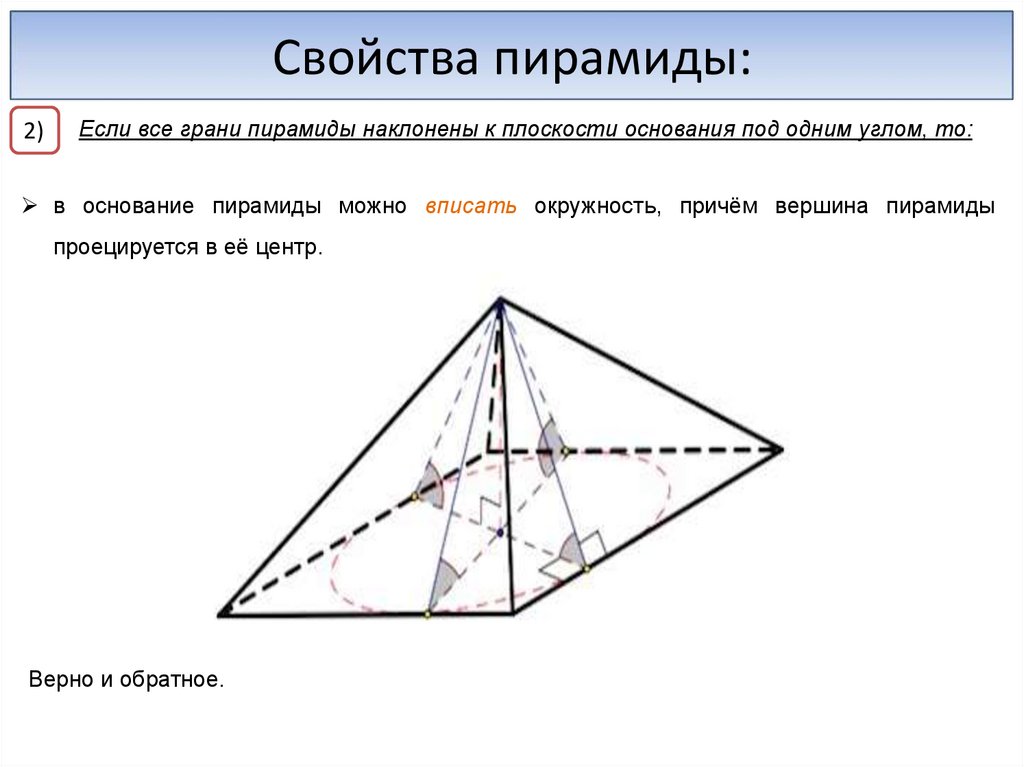
Свойства пирамиды:2)
Если все грани пирамиды наклонены к плоскости основания под одним углом, то:
в основание пирамиды можно вписать окружность, причём вершина пирамиды
проецируется в её центр.
Верно и обратное.
15.
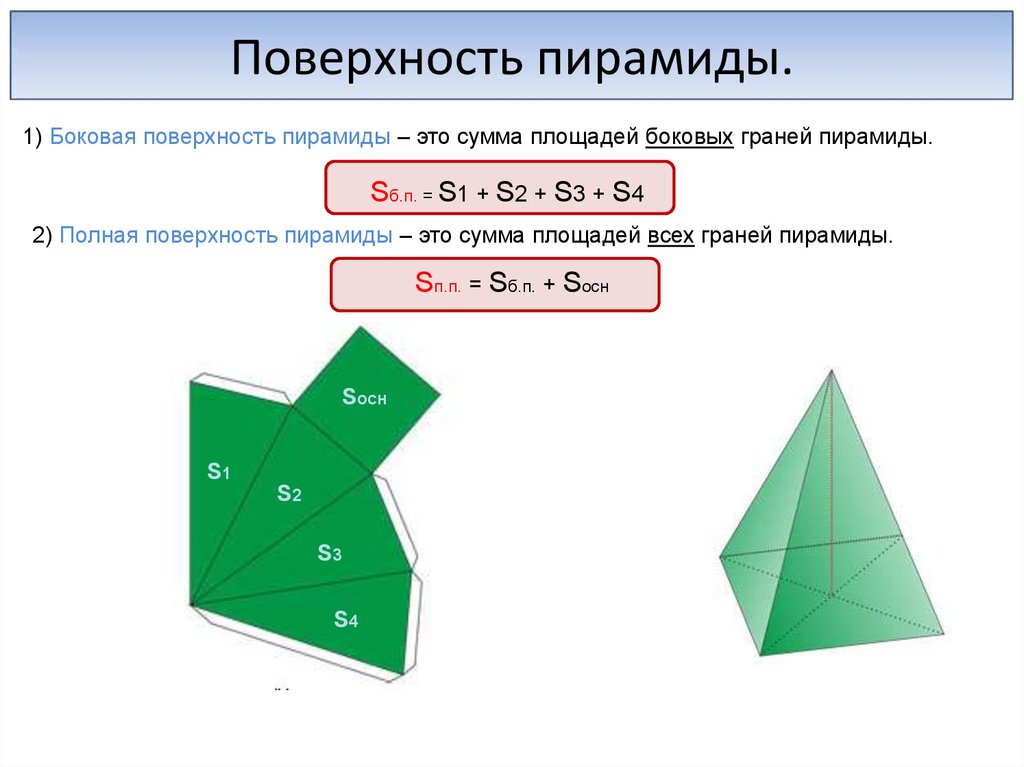
Поверхность пирамиды.1) Боковая поверхность пирамиды – это сумма площадей боковых граней пирамиды.
Sб.п. = S1 + S2 + S3 + S4
2) Полная поверхность пирамиды – это сумма площадей всех граней пирамиды.
Sп.п. = Sб.п. + Sосн
Sосн
S1
S2
S3
S4
16.
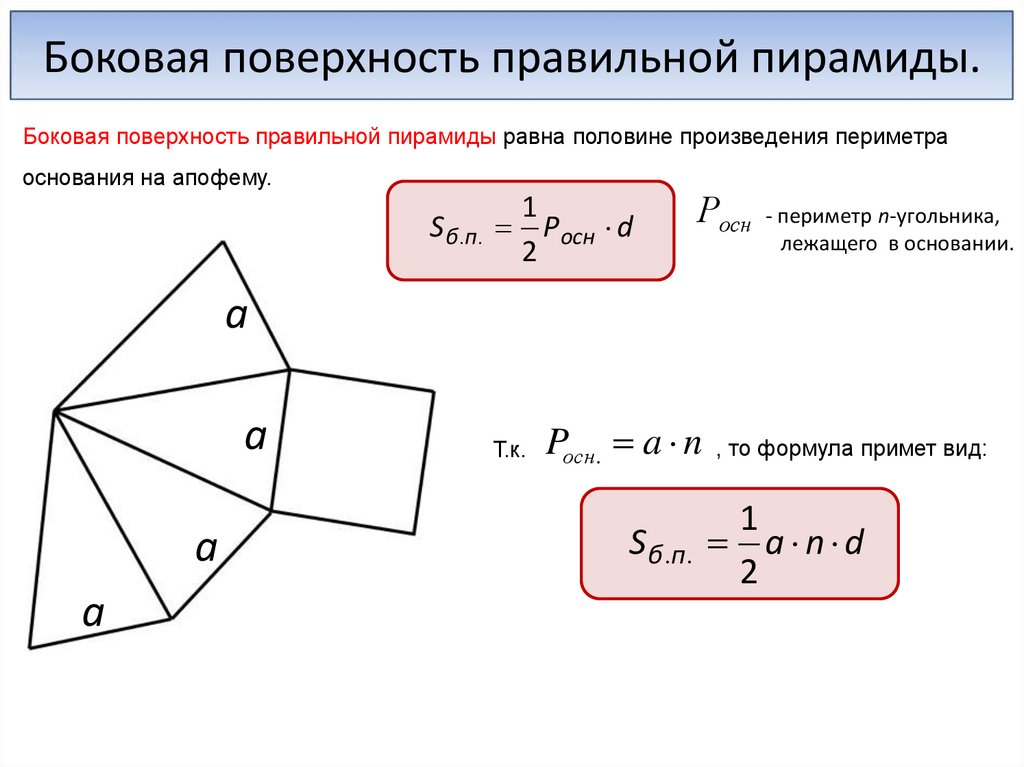
Боковая поверхность правильной пирамиды.Боковая поверхность правильной пирамиды равна половине произведения периметра
основания на апофему.
1
S б .п . Р осн d
2
Росн - периметр n-угольника,
лежащего в основании.
a
a
a
a
Т.к.
Pосн. a n , то формула примет вид:
1
Sб .п . a n d
2
17.
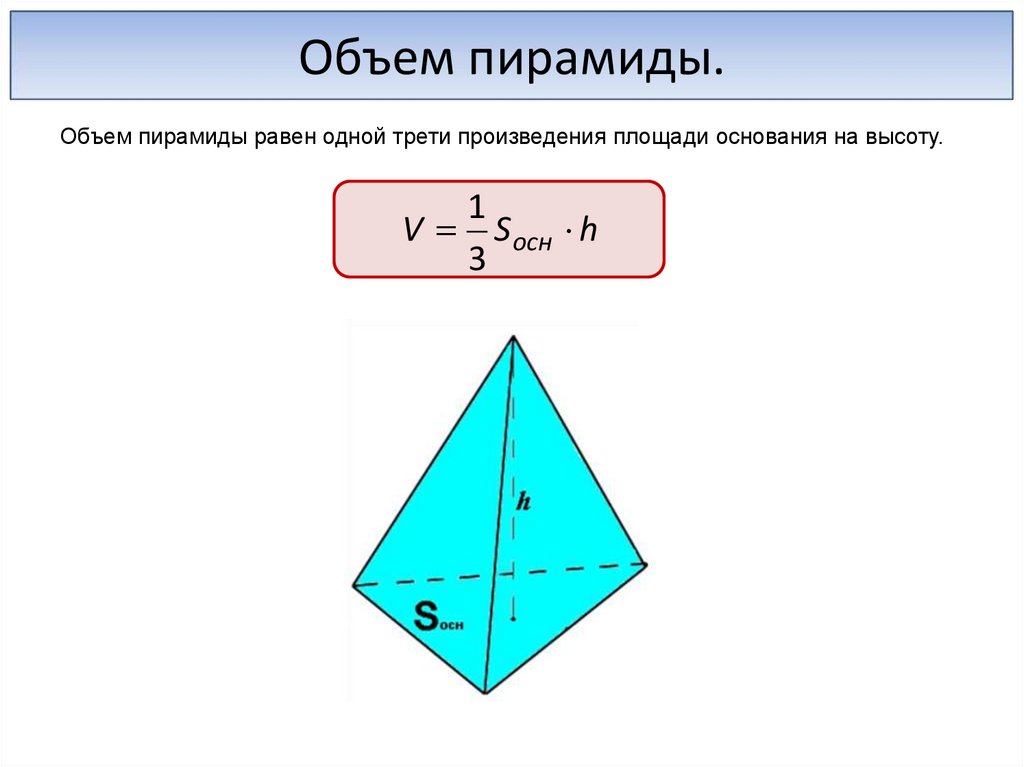
Объем пирамиды.Объем пирамиды равен одной трети произведения площади основания на высоту.
1
V S осн h
3
18.
Усеченная пирамида.19.
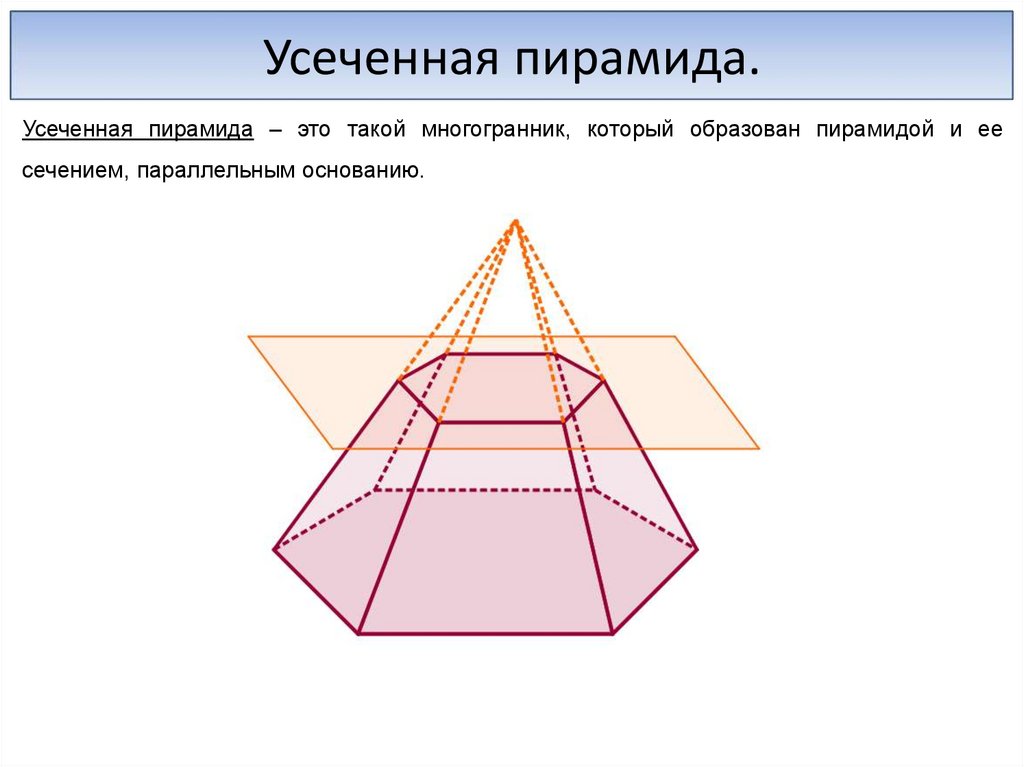
Усеченная пирамида.Усеченная пирамида – это такой многогранник, который образован пирамидой и ее
сечением, параллельным основанию.
20.
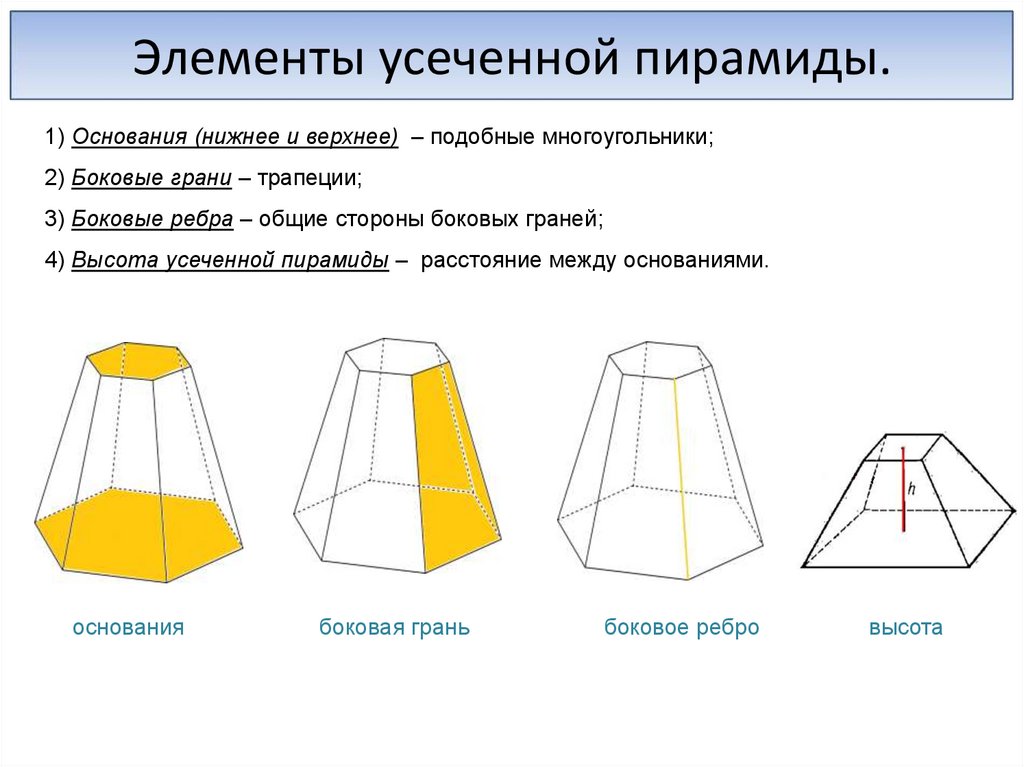
Элементы усеченной пирамиды.1) Основания (нижнее и верхнее) – подобные многоугольники;
2) Боковые грани – трапеции;
3) Боковые ребра – общие стороны боковых граней;
4) Высота усеченной пирамиды – расстояние между основаниями.
основания
боковая грань
боковое ребро
высота
21.
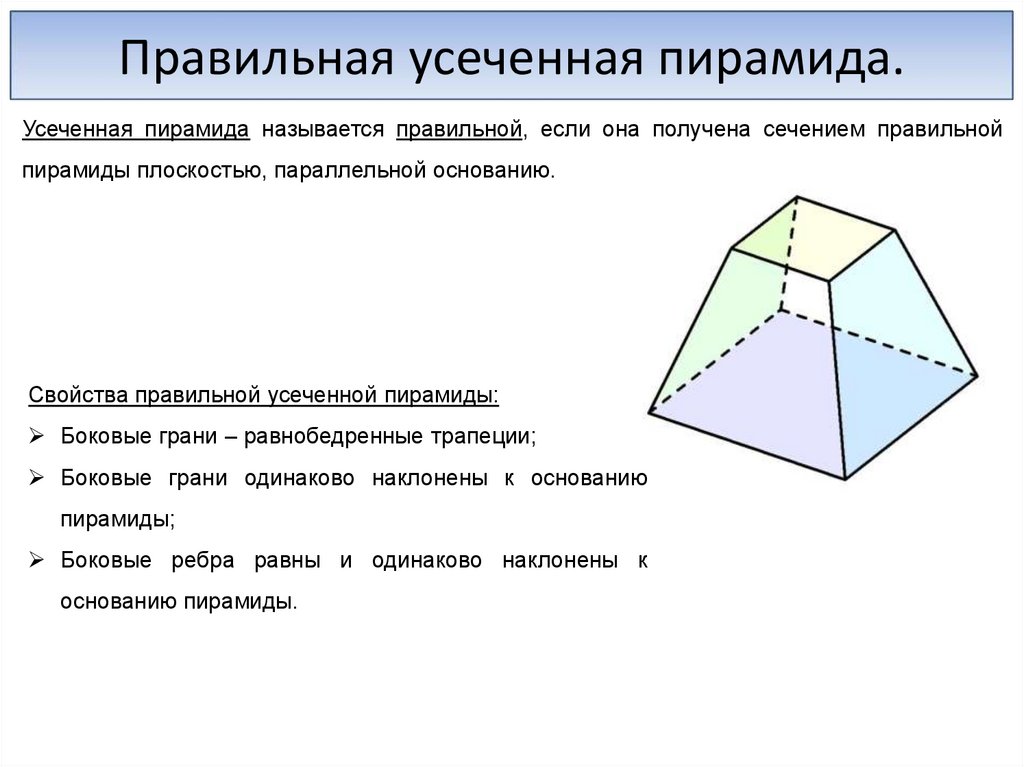
Правильная усеченная пирамида.Усеченная пирамида называется правильной, если она получена сечением правильной
пирамиды плоскостью, параллельной основанию.
Свойства правильной усеченной пирамиды:
Боковые грани – равнобедренные трапеции;
Боковые грани одинаково наклонены к основанию
пирамиды;
Боковые ребра равны и одинаково наклонены к
основанию пирамиды.
22.
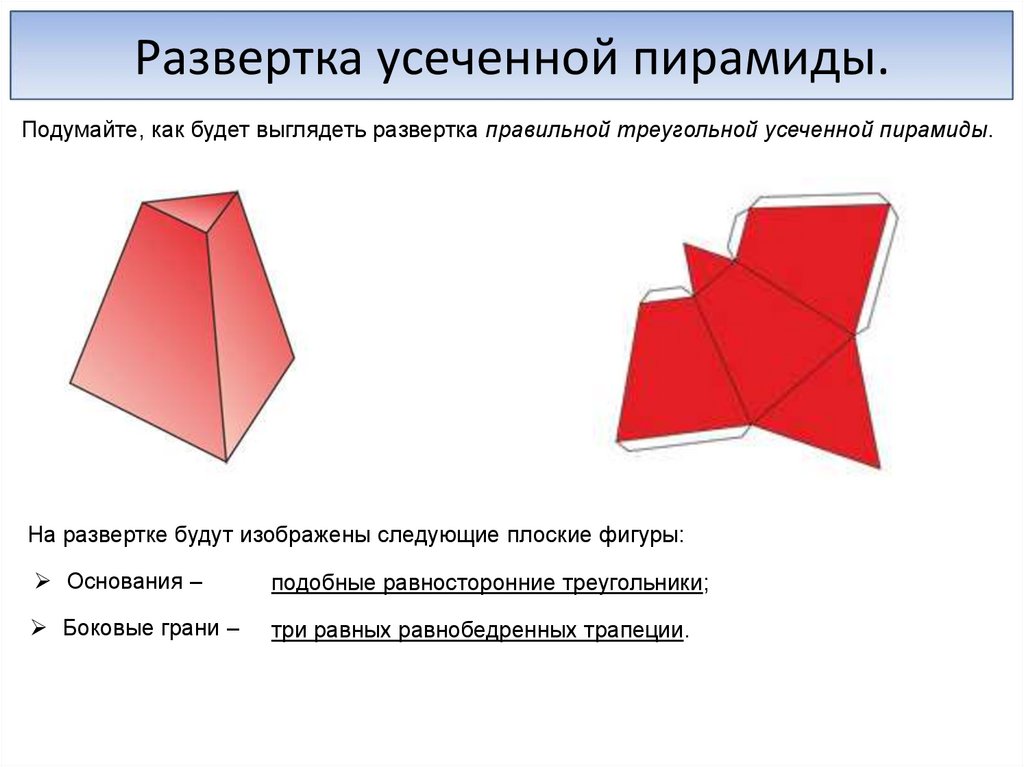
Развертка усеченной пирамиды.Подумайте, как будет выглядеть развертка правильной треугольной усеченной пирамиды.
На развертке будут изображены следующие плоские фигуры:
Основания –
подобные равносторонние треугольники;
Боковые грани –
три равных равнобедренных трапеции.
23.
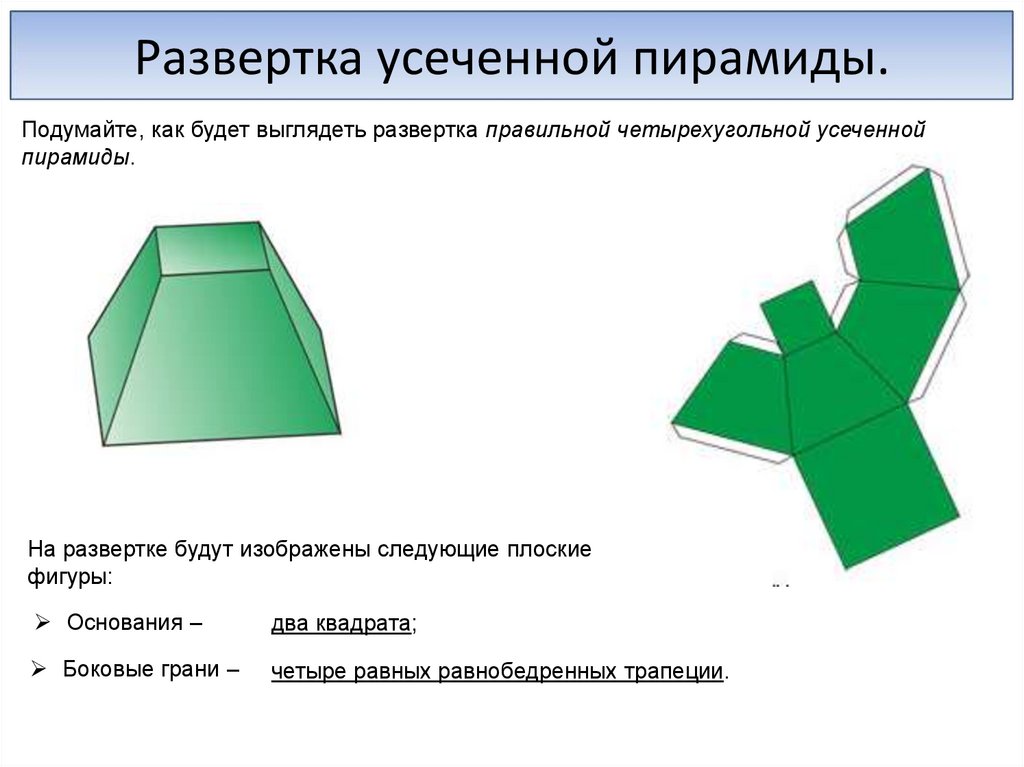
Развертка усеченной пирамиды.Подумайте, как будет выглядеть развертка правильной четырехугольной усеченной
пирамиды.
На развертке будут изображены следующие плоские
фигуры:
Основания –
два квадрата;
Боковые грани –
четыре равных равнобедренных трапеции.
24.
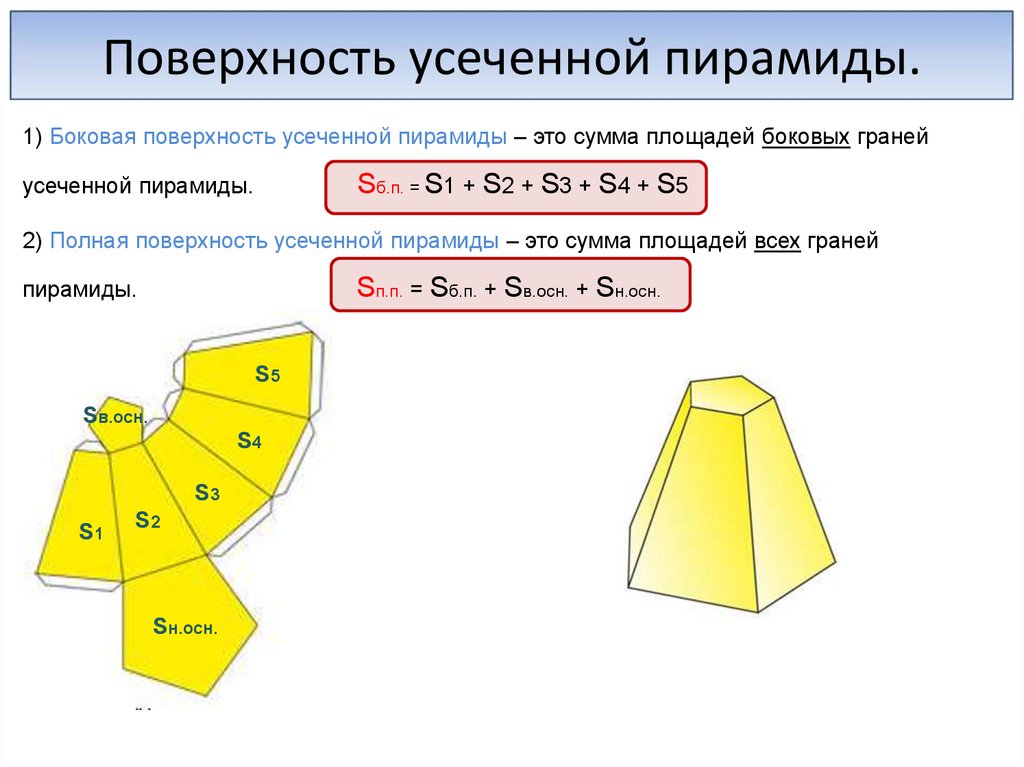
Поверхность усеченной пирамиды.1) Боковая поверхность усеченной пирамиды – это сумма площадей боковых граней
усеченной пирамиды.
Sб.п. = S1 + S2 + S3 + S4 + S5
2) Полная поверхность усеченной пирамиды – это сумма площадей всех граней
пирамиды.
Sп.п. = Sб.п. + Sв.осн. + Sн.осн.
S5
Sв.осн.
S4
S3
S1
S2
Sн.осн.
25.
Боковая поверхность правильной усеченной пирамиды.Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы
периметров оснований на апофему.
1
Sб .п. ( Рв .осн. Рн.осн. ) d
2
Рв .осн. - периметр верхнего основания
Рн.осн. - периметр нижнего основания
26.
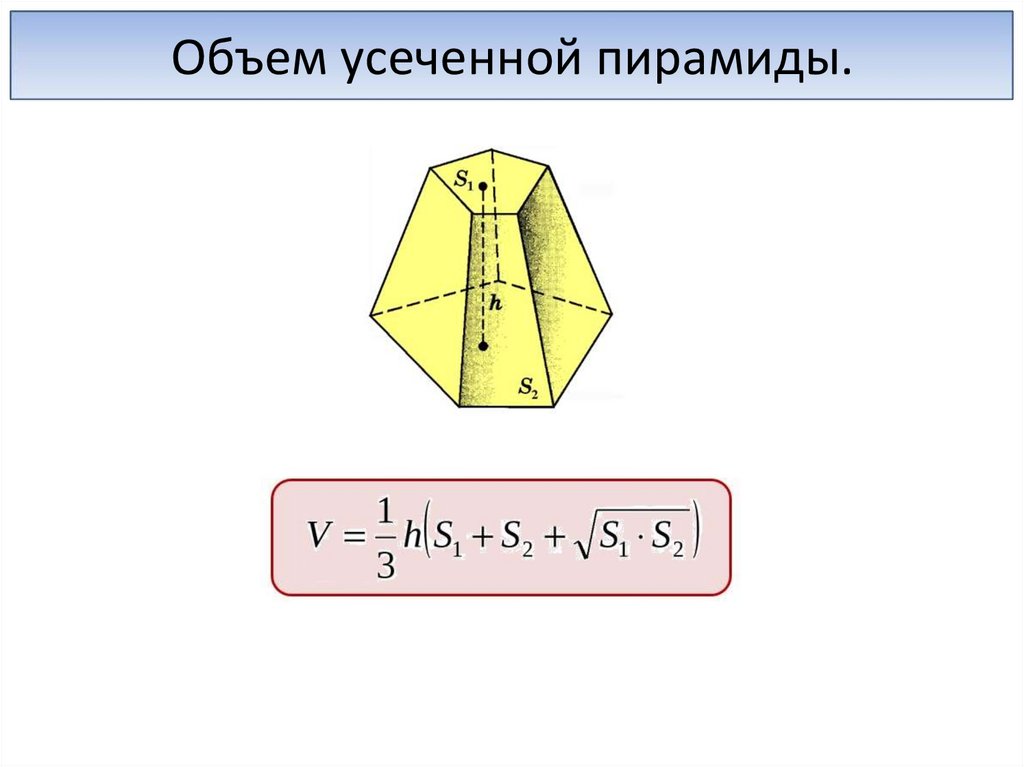
Объем усеченной пирамиды.27.
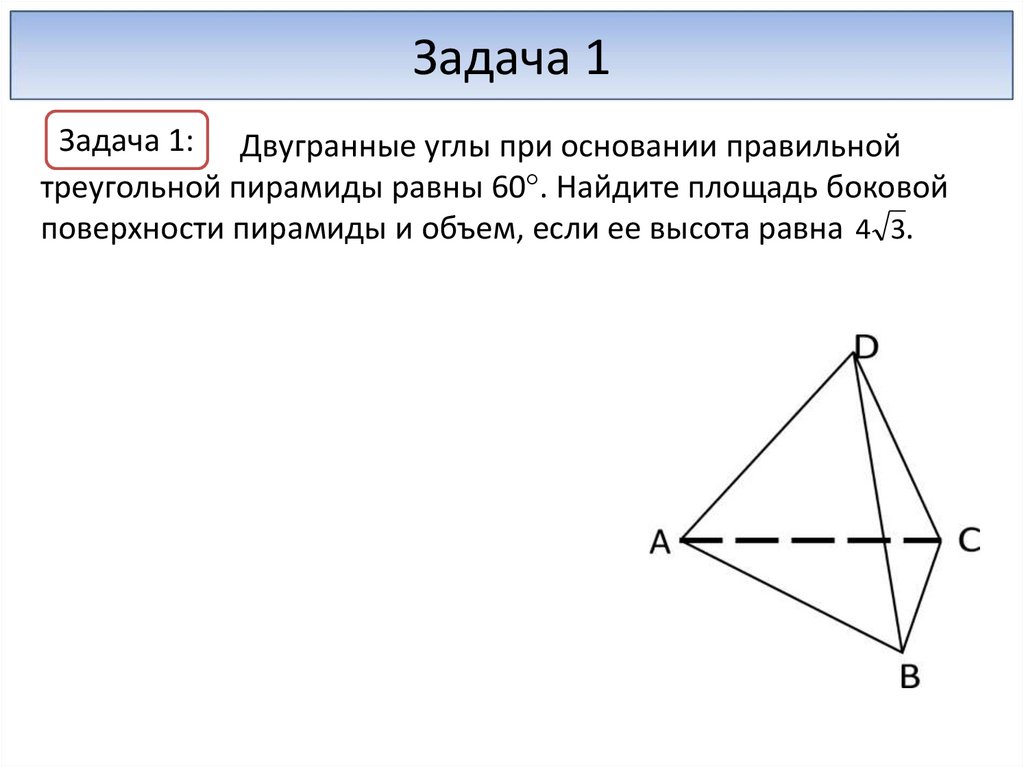
Задача 1Задача 1: Двугранные углы при основании правильной
треугольной пирамиды равны 60 . Найдите площадь боковой
поверхности пирамиды и объем, если ее высота равна 4 3.
28.
Задача 1ПЛАН РЕШЕНИЯ:
1. Определите, чем будет являться основание высоты DO пирамиды и постройте
высоту.
2. Вспомните свойство биссектрис равностороннего треугольника.
3. Найдите угол, который будет линейным углом двугранного угла, который
дан в задаче.
4. Найдите апофему пирамиды и длину ее проекции на основание.
5. Найдите длину биссектрисы треугольника АВС, а затем и сторону
треугольника АВС.
6. Найдите площадь боковой поверхности пирамиды и ее объем.
29.
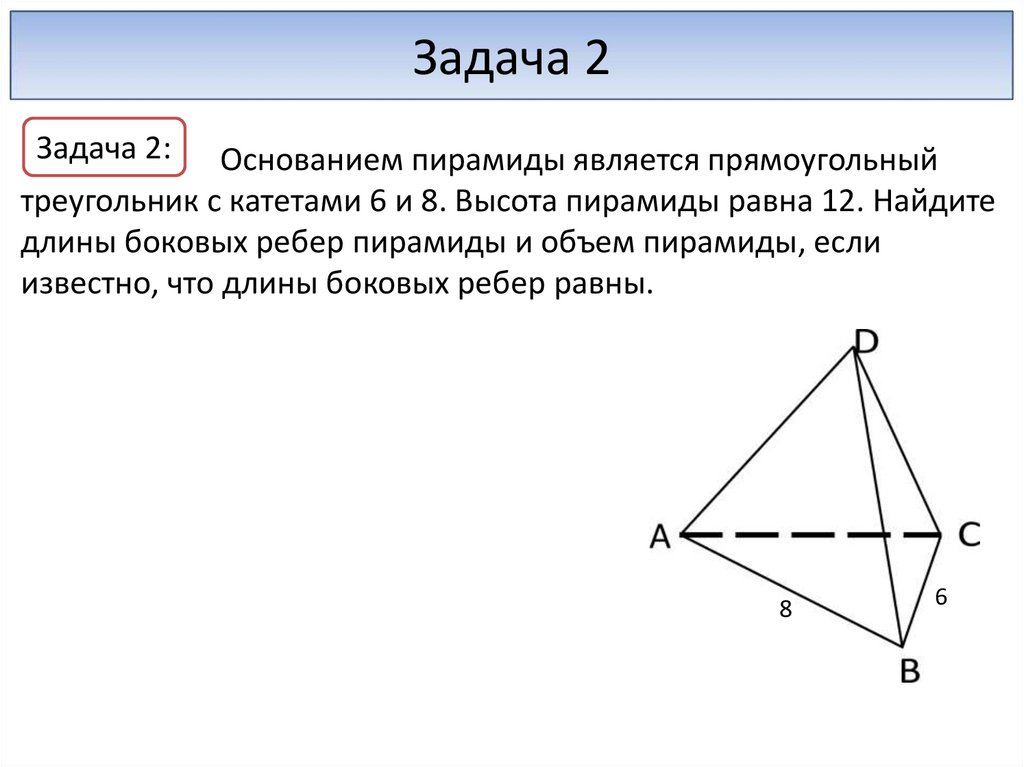
Задача 2Задача 2:
Основанием пирамиды является прямоугольный
треугольник с катетами 6 и 8. Высота пирамиды равна 12. Найдите
длины боковых ребер пирамиды и объем пирамиды, если
известно, что длины боковых ребер равны.
8
6
30.
Задача 2ПЛАН РЕШЕНИЯ:
1. Определите, чем будет являться основание высоты DO пирамиды и постройте
высоту.
2. Определите вид боковых граней пирамиды.
3. Найдите гипотенузу АС из треугольника АВС.
4. Найдите объем пирамиды.
5. Определите вид треугольника ОDC.
6. Найдите длину отрезка ОС.
7. Найдите длину гипотенузы DC из треугольника ODC.
31.
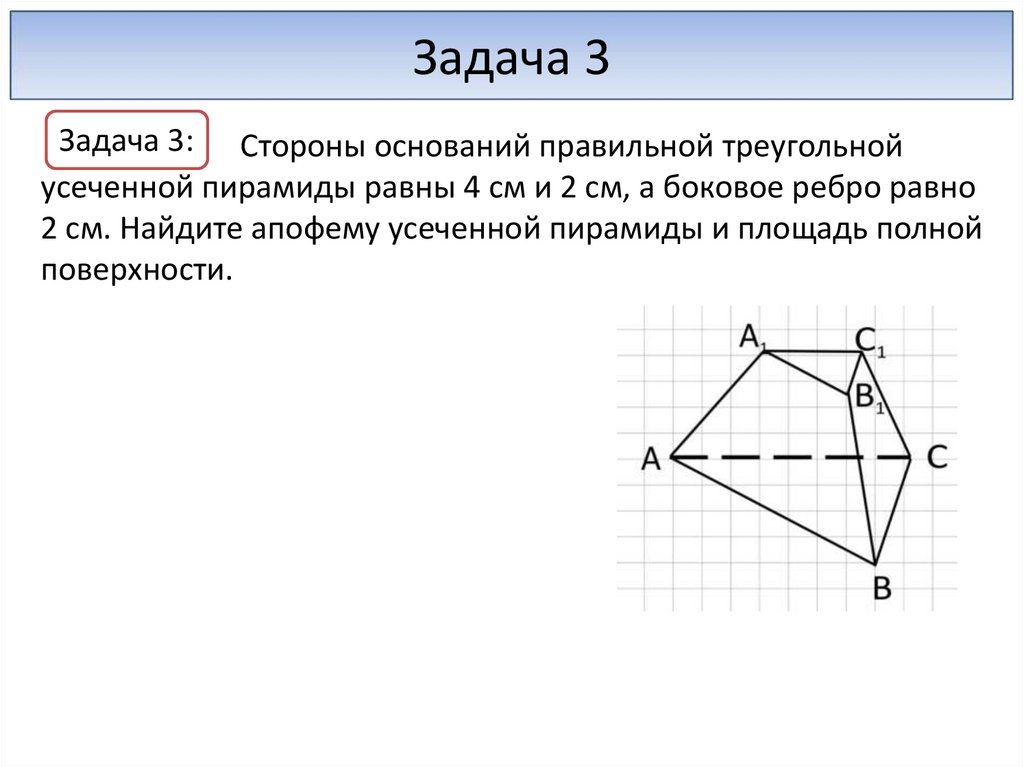
Задача 3Задача 3: Стороны оснований правильной треугольной
усеченной пирамиды равны 4 см и 2 см, а боковое ребро равно
2 см. Найдите апофему усеченной пирамиды и площадь полной
поверхности.
32.
Задача 3ПЛАН РЕШЕНИЯ:
1. Вспомните, какую фигуру представляет грань правильной усеченной пирамиды и
изобразите ее на плоскости.
2. Отметьте на этой фигуре все значения, которые даны в задаче.
3. Вспомните, что такое апофема и отметьте ее на изображенной фигуре.
4. Найдите апофему из прямоугольного треугольника.
5. Определите, какую фигуру представляют собой основания данной усеченной
пирамиды и изобразите их на плоскости.
6. Найдите площадь оснований удобным способом.
7. Найдите площадь боковой поверхности.
8. Найдите площадь полной поверхности.
33.
ОтветыЗадача 1.
Sб .п. 96 3, V 192
Задача 2.
Длины боковых ребер = 13, V 96
Задача 3.
3см, 14 3см 2 .









 mathematics
mathematics








