Пирамида

1.

ПИРАМИДА
Метапредмет – Знак

2.

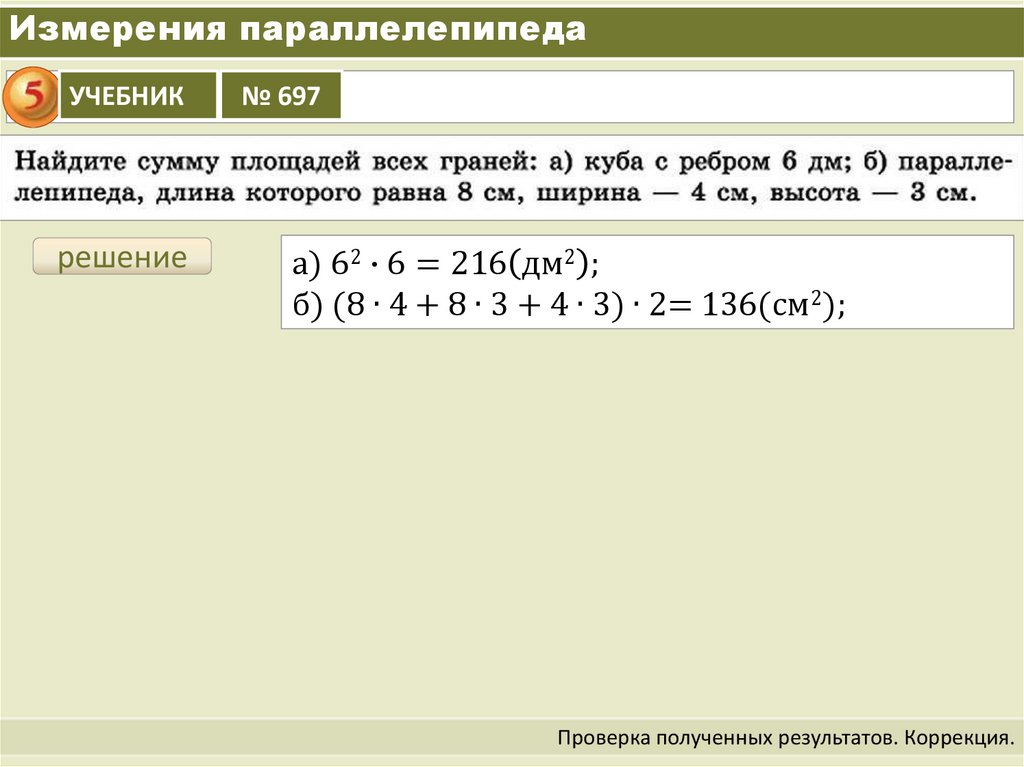
Измерения параллелепипеда
УЧЕБНИК
решение
№ 697
а) 62 ∙ 6 = 216 дм2 ;
б) (8 ∙ 4 + 8 ∙ 3 + 4 ∙ 3) ∙ 2= 136(см2);
Проверка полученных результатов. Коррекция.

3.

Ключевое слово урока
Форму пирамид имели гробницы фараонов в Древнем Египте.
Древнеегипетские пирамиды сохранились до наших дней. Одна
из самых знаменитых – пирамида Хеопса, высота которой
достигает 147 м. сооружения, похожие на египетские пирамиды,
строили и древние майя, жившие на американском континенте.
Их храмы имели форму усеченной пирамиды.
целеполагание

4.

Пирамида
Стр. 191
Простейшей пирамидой является треугольная
пирамида. Все ее грани – треугольники, и каждая
из них может считаться ее основанием. У
треугольной пирамиды 4 грани, 6 ребер и 4
вершины
Организация и самоорганизация учащихся. Организация обратной связи

5.

Работаем с моделями
ТРЕНАЖЕР
№ 245
ABCD
EABCD
AE, BE, CE, DE
ABE, CBE, CDE, ADE
решение
Практикум

6.

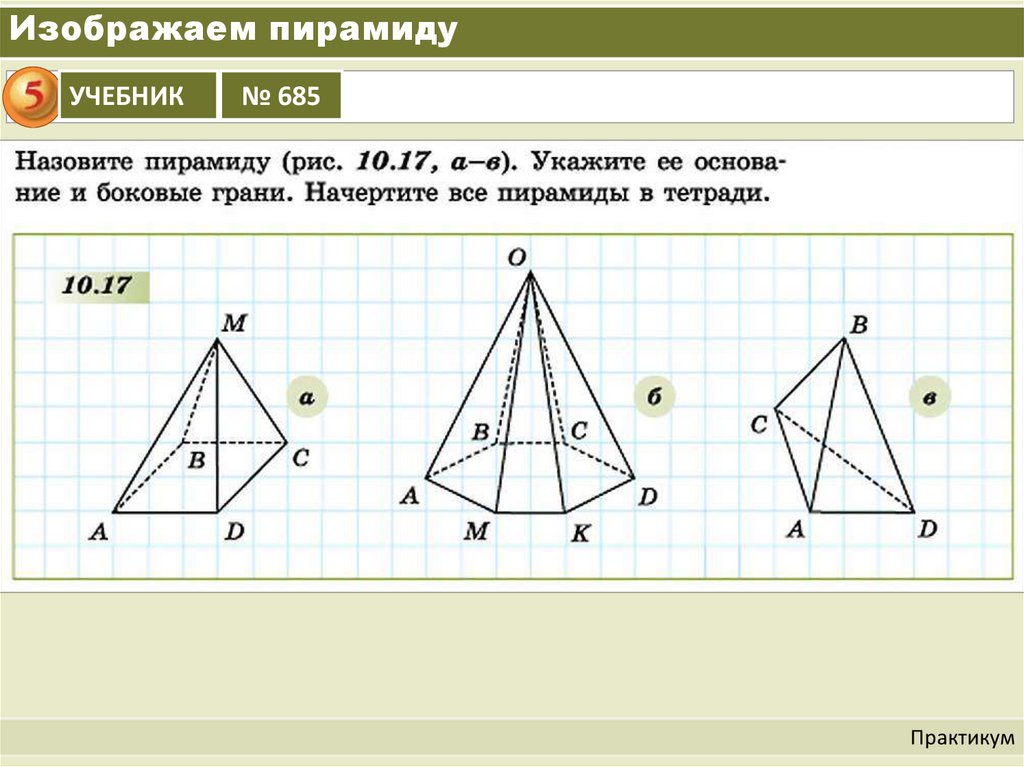
Изображаем пирамиду
УЧЕБНИК
№ 685
Практикум

7.

Осваиваем алгоритмы
ТРЕНАЖЕР
№ 259
решение
Практикум

8.

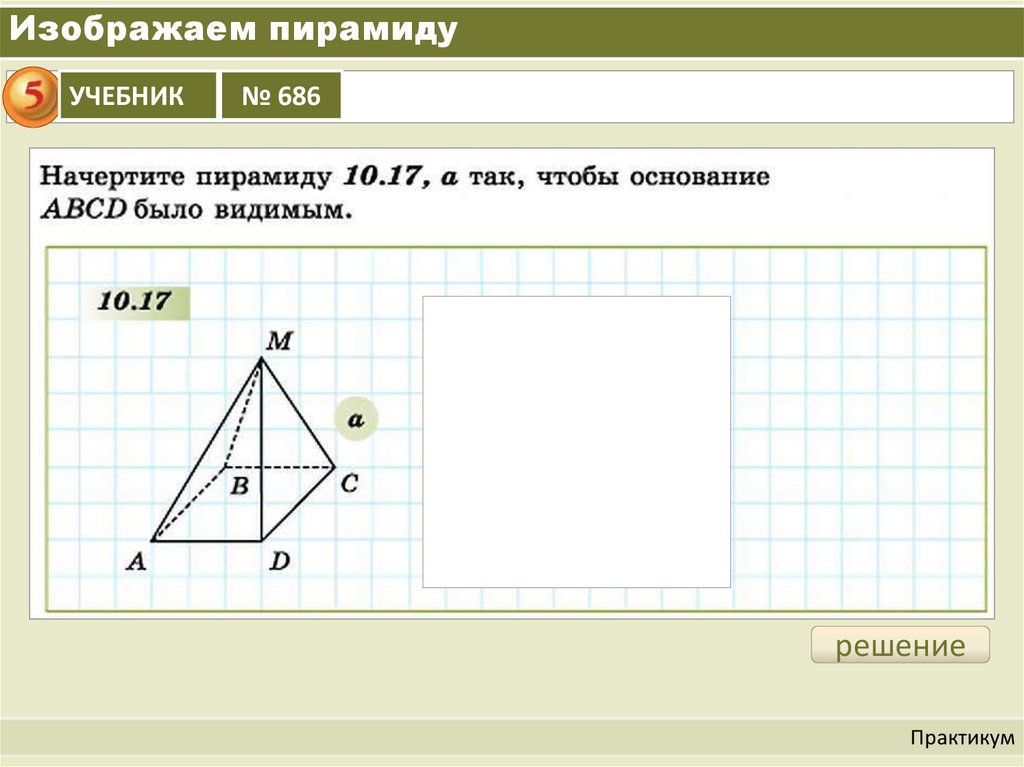
Изображаем пирамиду
УЧЕБНИК
№ 686
решение
Практикум

9.

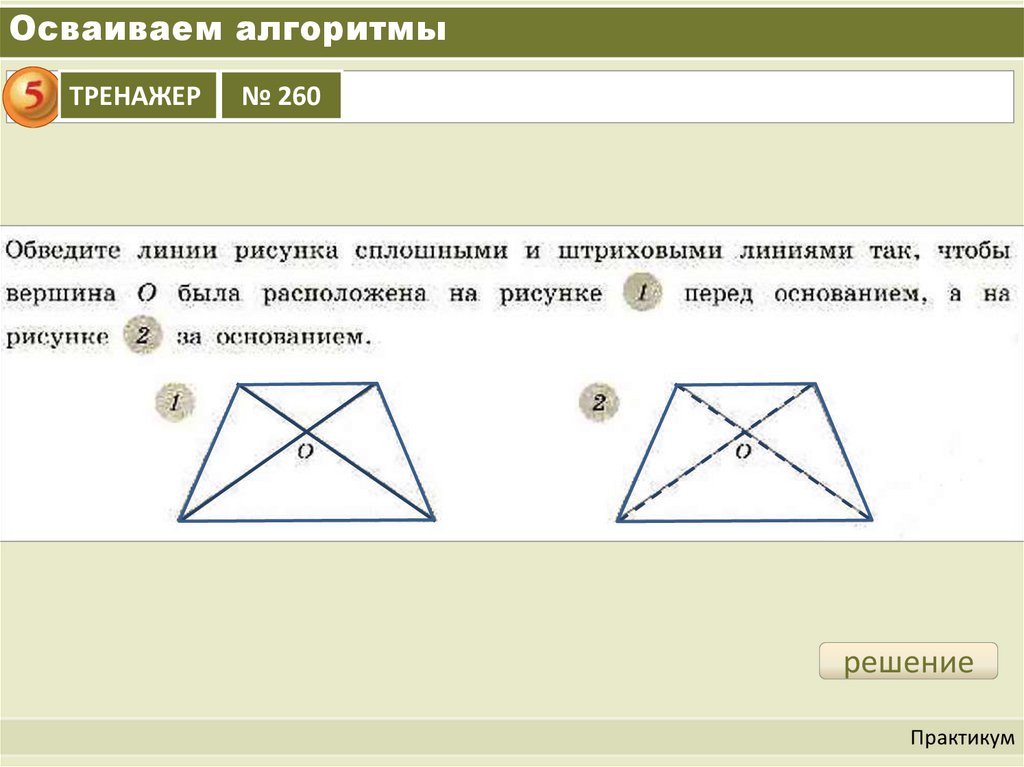
Осваиваем алгоритмы
ТРЕНАЖЕР
№ 260
решение
Практикум

10.

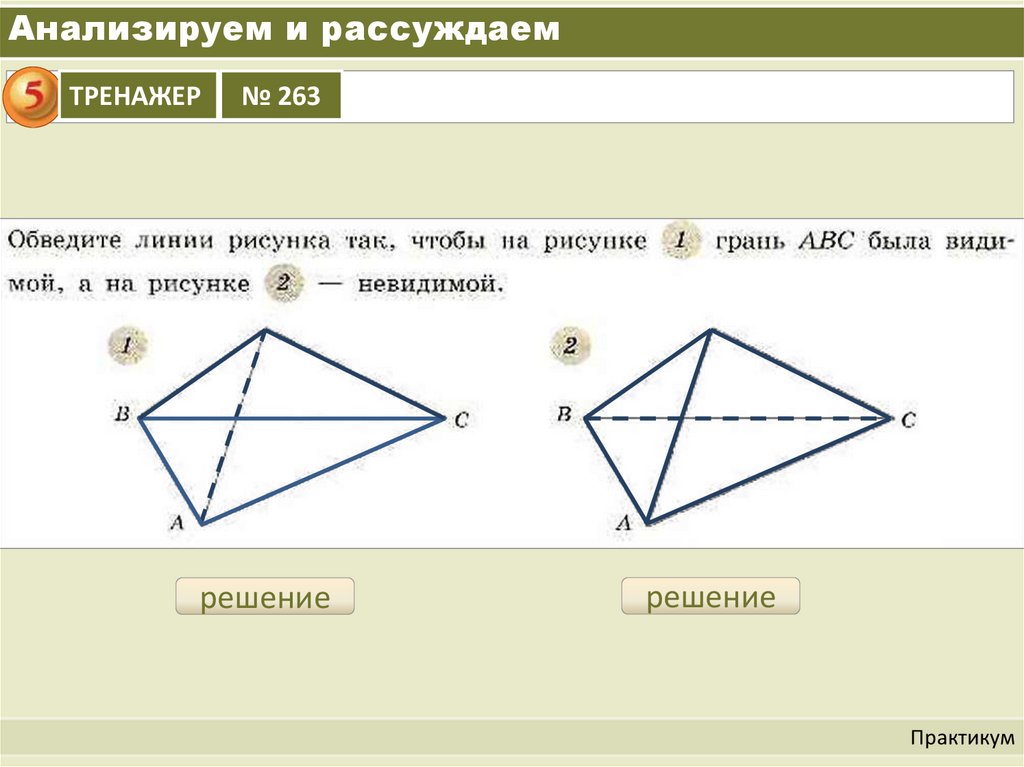
Анализируем и рассуждаем
ТРЕНАЖЕР
№ 263
решение
решение
Практикум

11.

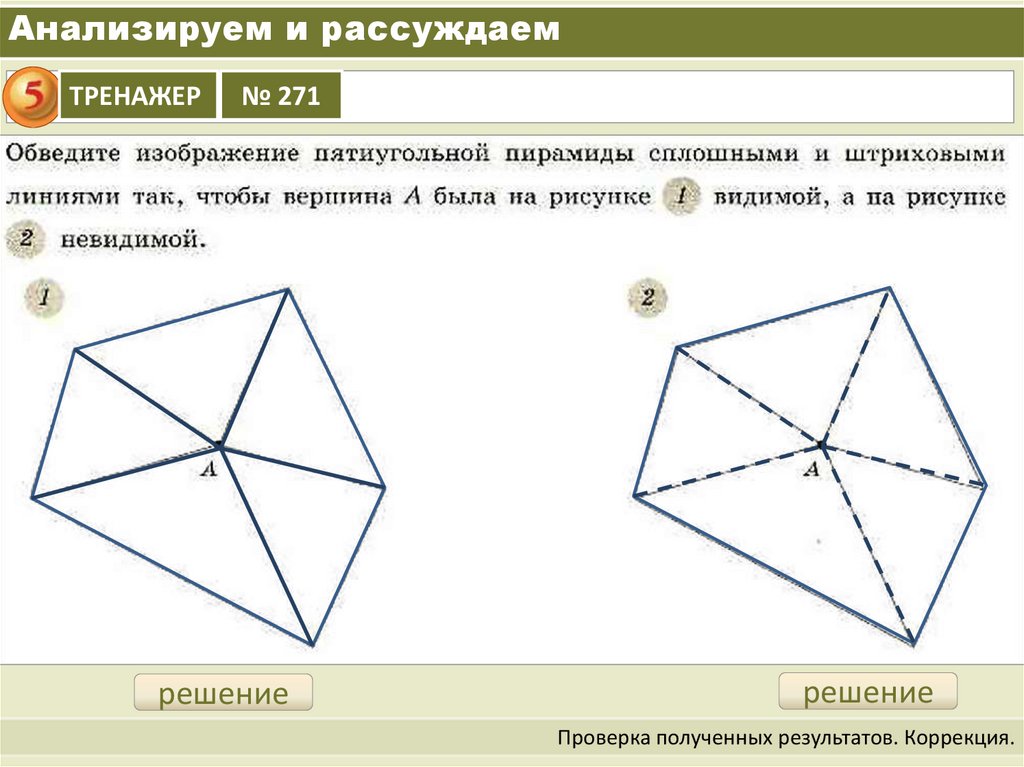
Анализируем и рассуждаем
ТРЕНАЖЕР
№ 271
решение
решение
Проверка полученных результатов. Коррекция.

12.

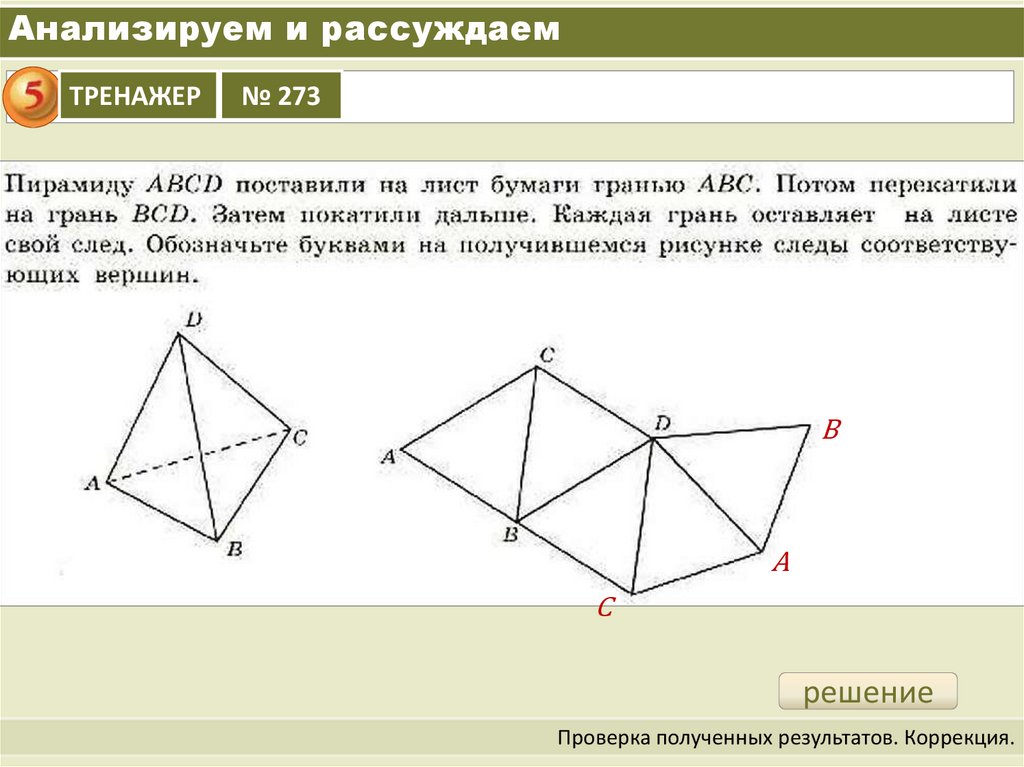
Анализируем и рассуждаем
ТРЕНАЖЕР
№ 273
B
A
C
решение
Проверка полученных результатов. Коррекция.

13.

Ребра, грани и вершины (продвинутым)
УЧЕБНИК
№ 693
1) 1882 вершины;
2) Девятисотугольная;
3) 28 вергин
4) Нет;
5) Восьмиугольная.
решение
Проверка полученных результатов. Коррекция.

14.

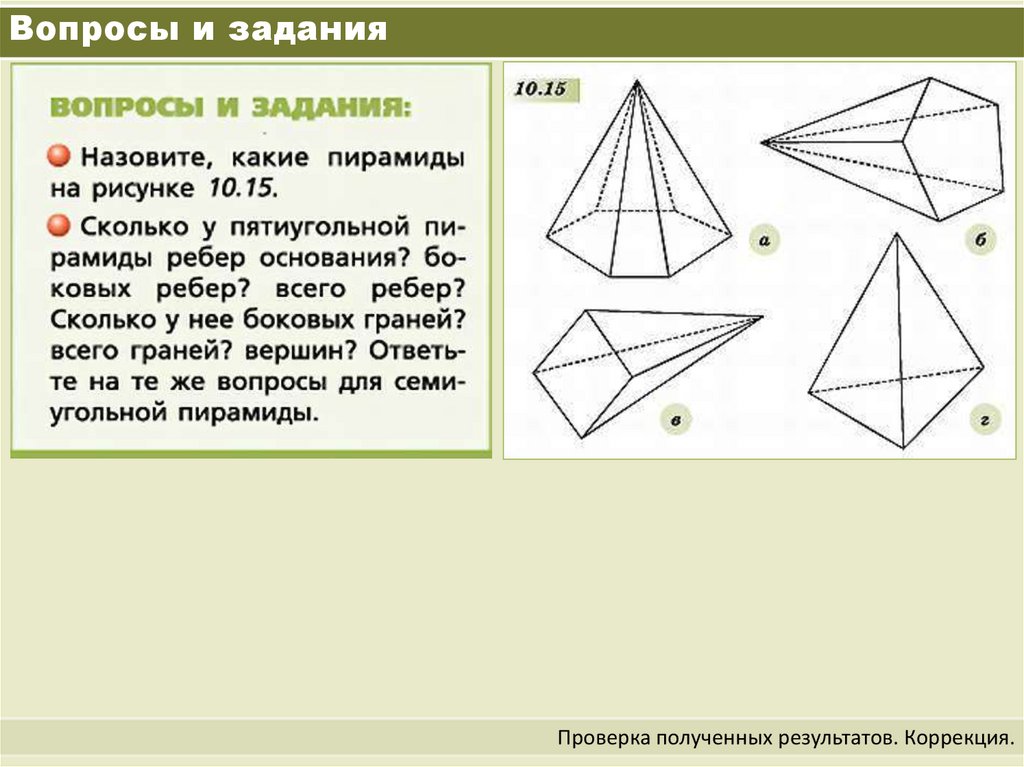
Вопросы и задания
Проверка полученных результатов. Коррекция.

15.

Анализируем и рассуждаем
ТРЕНАЖЕР
№ 270
решение
решение
Практикум

16.

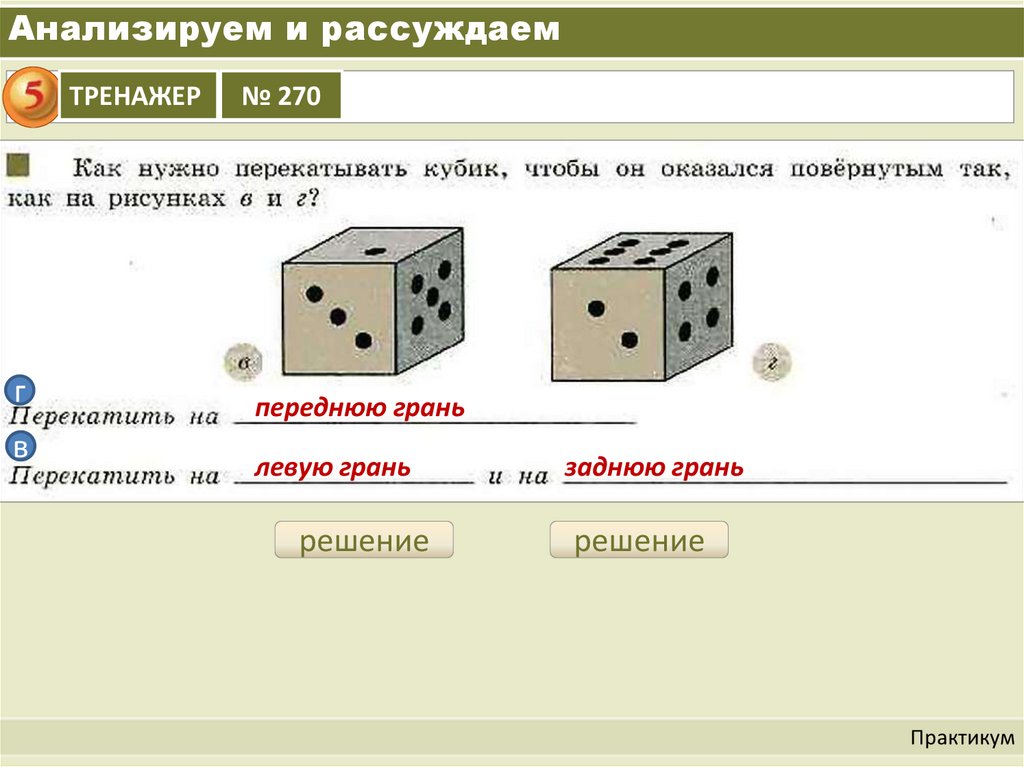
Анализируем и рассуждаем
ТРЕНАЖЕР
г
в
№ 270
переднюю грань
левую грань
решение
заднюю грань
решение
Практикум

17.

Итоги нашего урока
Древнегреческий ученый Евклид говорил: «Это телесная фигура,
ограниченная плоскостями, которые от одной плоскости
(основания) сходятся к одной точке (вершине)».
Герон утверждал, что «Это фигура, ограниченная треугольниками,
сходящимися в одной точке, и основанием которой служит
многоугольник».
Английский математик Тейлор писал, что «Это многогранник, у
которого все грани, кроме одной,
сходятся в одной точке».
Что это за фигура?
Музей Лувр, Франция
Домашнее задание
У: стр. 191, фрагмент 2 – читать; «Вопросы и задания» : № 4,
5; № 687, 689, 691; Т: № 272. Подведение итогов, рефлексия, домашнее задание.