Similar presentations:
Волны, виды волн
1.
ВОЛНЫВИДЫ ВОЛН.
УРАВНЕНИЯ ПЛОСКОЙ И СФЕРИЧЕСКОЙ ВОЛН.
Волна - процесс распространения колебаний в пространстве.
Виды волн:
- продольные;
- поперечные.
2.
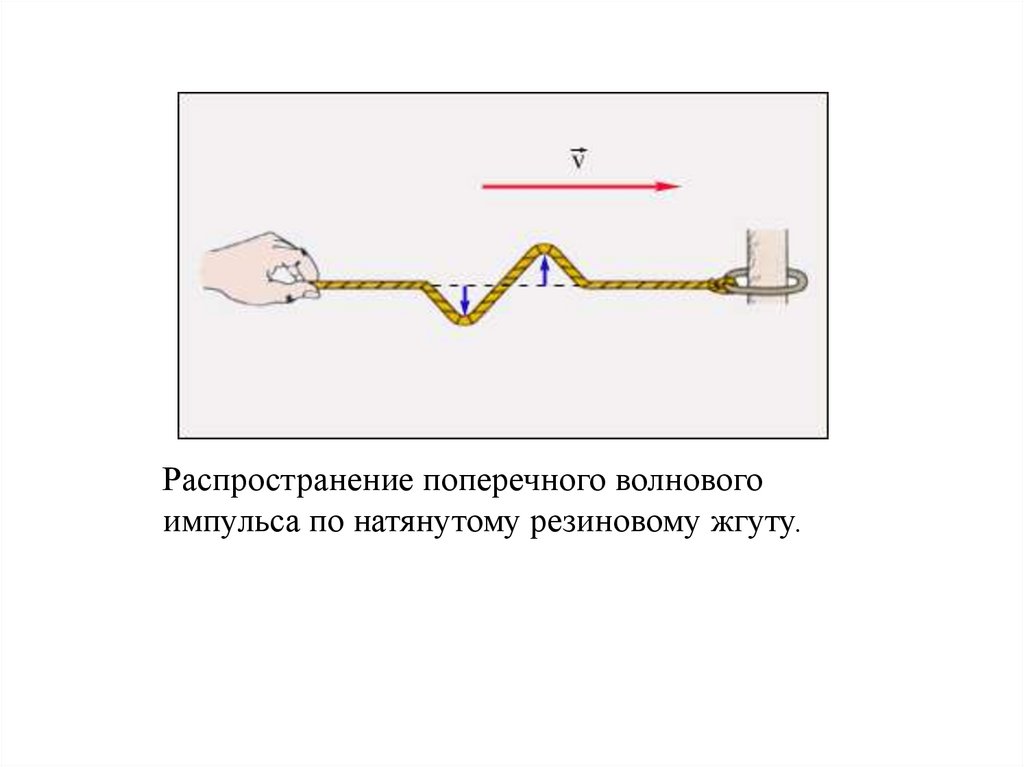
Распространение поперечного волновогоимпульса по натянутому резиновому жгуту.
3.
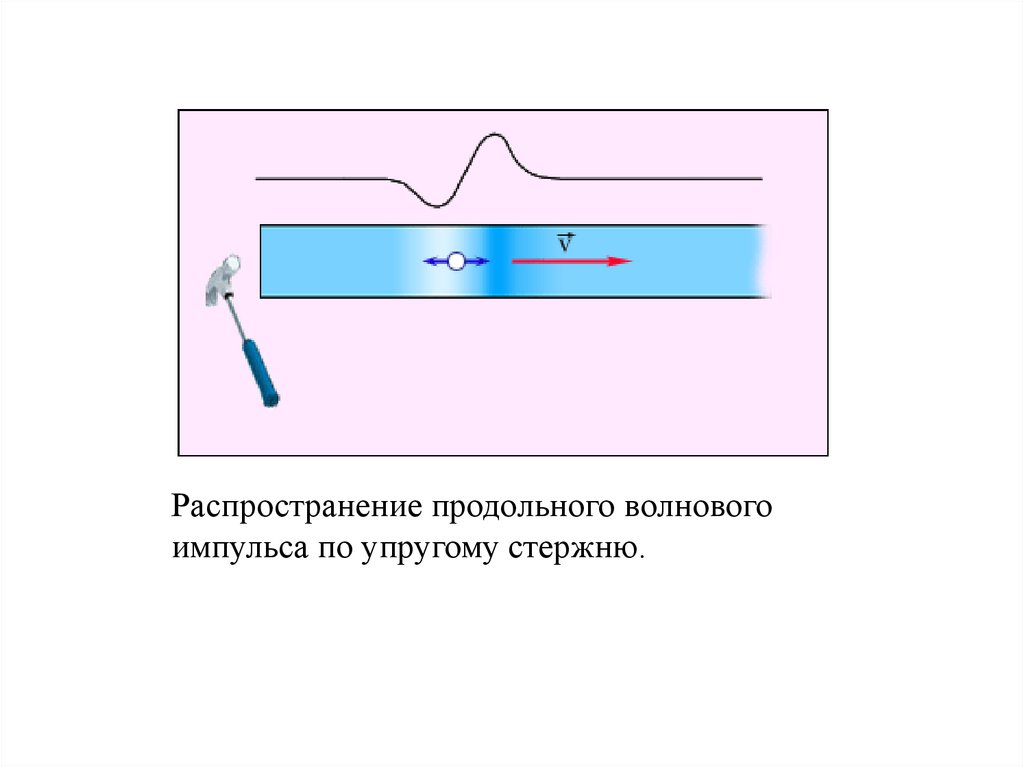
Распространение продольного волновогоимпульса по упругому стержню.
4.
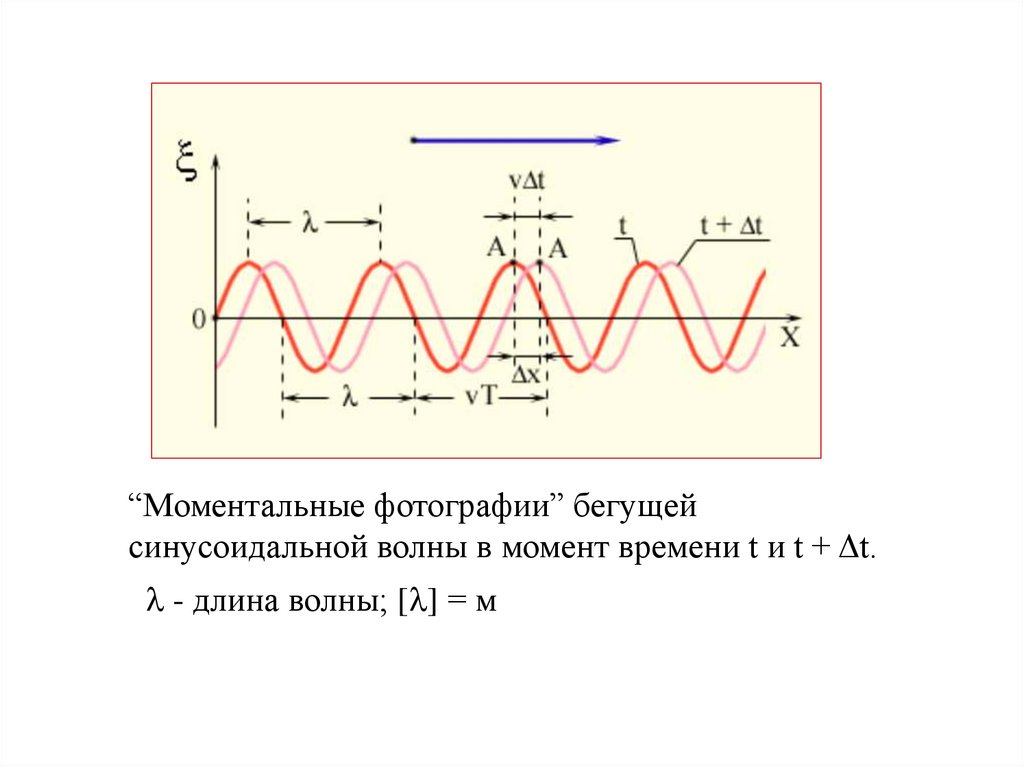
“Моментальные фотографии” бегущейсинусоидальной волны в момент времени t и t + Δt.
- длина волны; [ ] = м
5.
T1
T
:
С учетом
Фронт волны:
геометрическое место точек, до которых дошли колебания
в данный момент времени.
Волновая поверхность:
геометрическое место точек, колеблющихся в одинаковой
фазе. (волны: плоские, сферические и др.)
6.
( x, y, z, t ) - уравнение волныРассмотрим плоскую волну, распространяющуюся в
направлении оси Х:
7.
( x 0, t ) A cos( t )x
( x, t ) A cos[ ( t ) ]
x
( x, t ) A cos[ ( t ) ]
- фазовая скорость, т.е. скорость с которой
перемещается данное значение фазы.
dx
При фиксированной фазе:
dt
8.
x( x, t ) A cos[ t ]
2
k
- волновое число
A cos[ t kx ]
2 2
k
- незатухающая волна
A 0 e x cos[ t kx ]
- затухающая волна
(в поглощающей среде)
9.
Рассмотрим сферическую волнуФаза волны для точек, лежащих на волновой
поверхности радиуса r:
r
[ ( t ) ] t kr
Уравнение сферической волны в непоглощающей среде:
A
cos( t kr )
r
Уравнение сферической волны в поглощающей среде:
A r
e cos( t kr )
r
10.
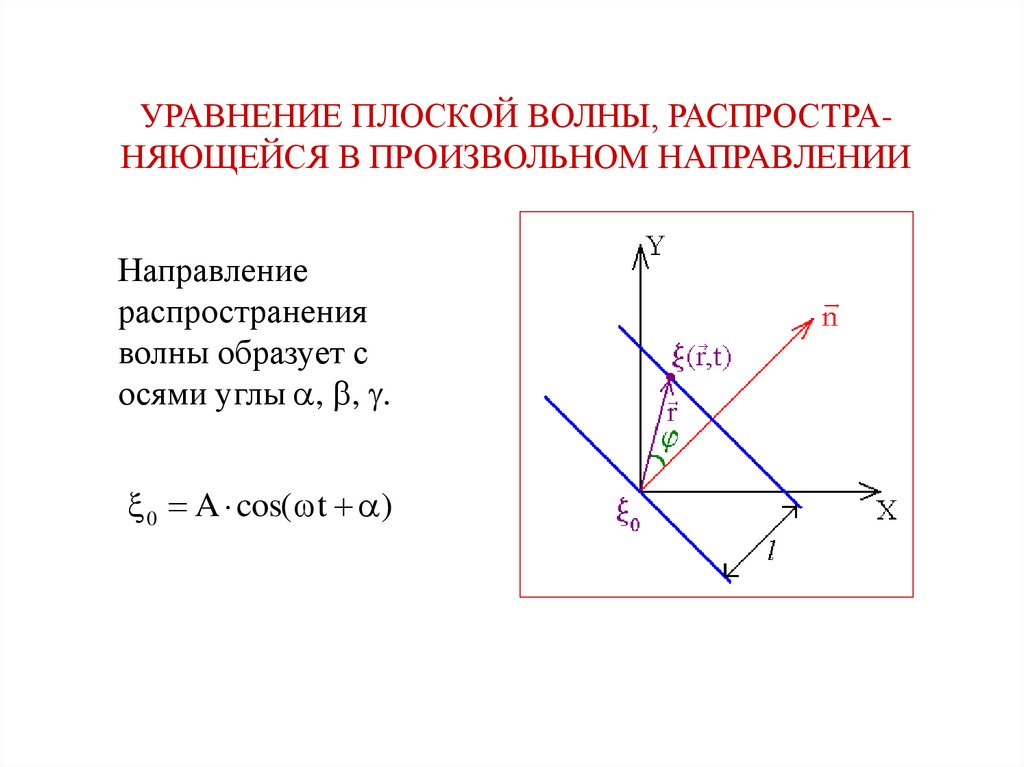
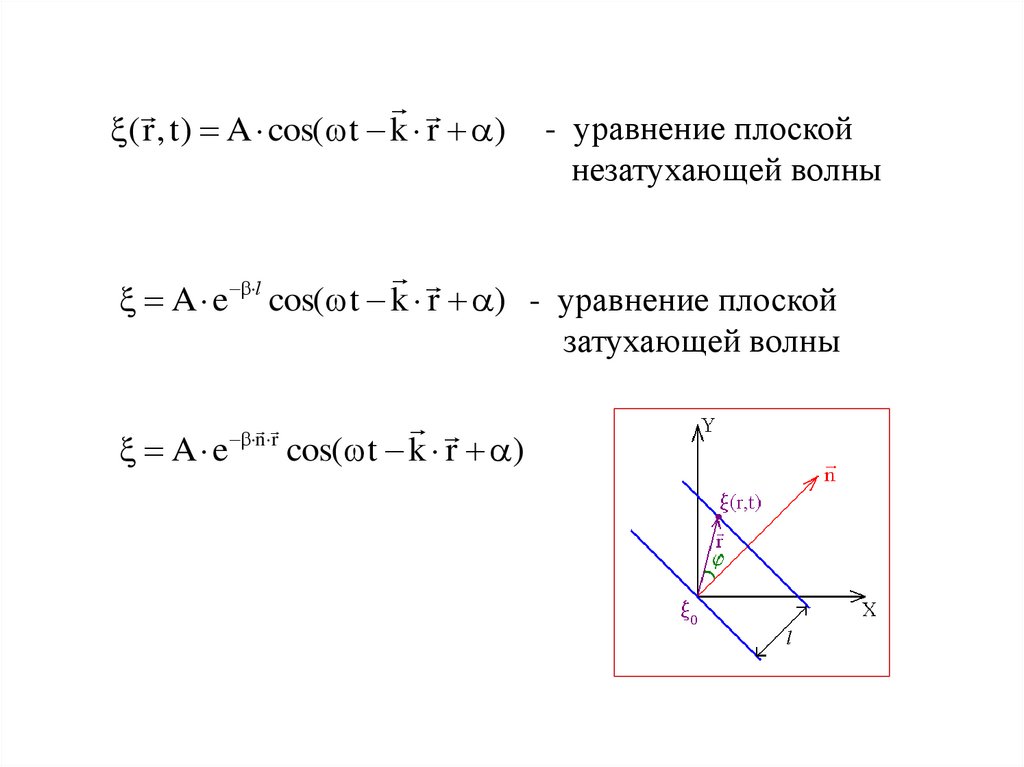
УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИНаправление
распространения
волны образует с
осями углы , , .
0 A cos( t )
11.
lA cos( ( t ) )
A cos( t k l )
Для произвольной точки волновой поверхности:
n r 1 r cos l
A cos( t k n r )
k k n - волновой вектор
2
k k
12.
( r , t ) A cos( t k r )- уравнение плоской
незатухающей волны
cos( t k r ) - уравнение плоской
затухающей волны
A e
l
A e
n r
cos( t k r )
13.
Перепишем через координаты уравнение:( r , t ) A cos( t k r )
k r k (x i y j z k)
k x i k y j k z k
k x 1 cos k y 1 cos k z 1 cos
kx x k y y kz z
14.
( x, y, z, t ) A cos( t k x x k y y k z z )2
k x cos
2
k y cos
2
k z cos
15.
ВОЛНОВОЕ УРАВНЕНИЕУравнение волны является решением волнового уравнения.
Получим волновое уравнение.
( r , t ) A cos( t k r )
( x, y, z, t ) A cos( t k x x k y y k z z )
2
( A sin( t k r ) )
2
t
t
2
A cos( t k r ) 2
16.
( r , t ) A cos( t k r )( x, y, z, t ) A cos( t k x x k y y k z z )
2
(A sin( t k r ) k x )
2
x
x
2
2
k x A cos( t k r ) k x
2
( A sin( t k r ) k y )
y 2 y
2
k 2y A cos( t k r ) k y
2
(A sin( t k r ) k z )
2
z
z
2
2
k z A cos( t k r ) k z
17.
2 2 22
2
2
2
(
k
k
k
)
k
x
y
z
2
2
2
x y z
2
2
2
t
1 2
2 2
t
2 2 2 k 2 2 1 2
2 2 2 2 2 2
2
x y z
t
t
k2 1
(k ; 2 2 )
18.
2 2 2 1 22 2 2 2
2
x y z
t
1
2 2
t
2
2 2 2
2 2 2
x y z
Для плоской волны, распространяющейся в направлении х:
2 1 2
2 2
2
x
t
19.
E- фазовая скорость продольной волны
Е - модуль Юнга
G
- фазовая скорость поперечной волны
G - модуль сдвига
20.
ЭНЕРГИЯ УПРУГОЙ ВОЛНЫРассмотрим плоскую продольную волну, распространяющуюся в направлении х:
A cos[ t kx )]
Среда, в которой распространяется волна, обладает
дополнительным запасом энергии. Волна переносит
энергию от источника колебаний в различные точки
среды.
21.
Плотность энергии:W
w
V
w A 2 2 sin 2 ( t kx )
Среднее по времени значение:
1
w A 2 2
2
22.
Поток энергии через заданную поверхность(скалярная величина):
W
dW
[ ] Вт
t
dt
Плотность потока энергии (векторная величина):
W
j
S t
j dS
[ j ] Вт / м
2
j w
23.
Определим вектор v , модуль которого равен фазовойскорости волны, а направление совпадает с
направлением переноса энергии (вектор скорости
переноса энергии).
j w v
Для синусоидальных волн эта скорость равна фазовой:
j w
j - вектор Умова.
24.
Среднее по времени значение вектора Умова:j w
1
2
2
j A
2
1
I j A2 2 - интенсивность волны
2
I ~ A2
25.
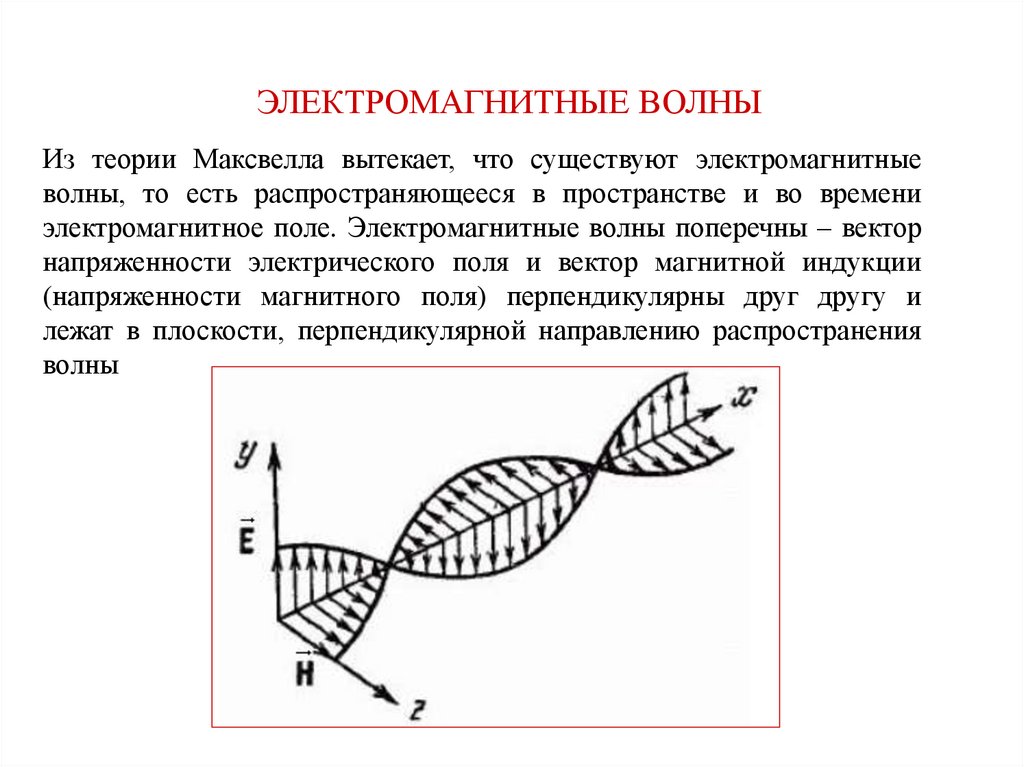
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫИз теории Максвелла вытекает, что существуют электромагнитные
волны, то есть распространяющееся в пространстве и во времени
электромагнитное поле. Электромагнитные волны поперечны – вектор
напряженности электрического поля и вектор магнитной индукции
(напряженности магнитного поля) перпендикулярны друг другу и
лежат в плоскости, перпендикулярной направлению распространения
волны
26.
27.
Волновое уравнение для электромагнитной волны:2
2
2
E E E E
x 2 y 2 z 2 c 2 t 2
2
2
2
2
H H H H
x 2 y 2 z 2 c 2 t 2
2
28.
29.
Электромагнитные волны распространяются в веществе с конечнойскоростью.
c
n
c
n
30.
31.
Закон отражения электромагнитных волн.Угол падения равен углу преломления и лежат в одной плоскости
1 2
Закон преломления электромагнитных волн.
sin n2
n21
sin n1
32.
33.
34.
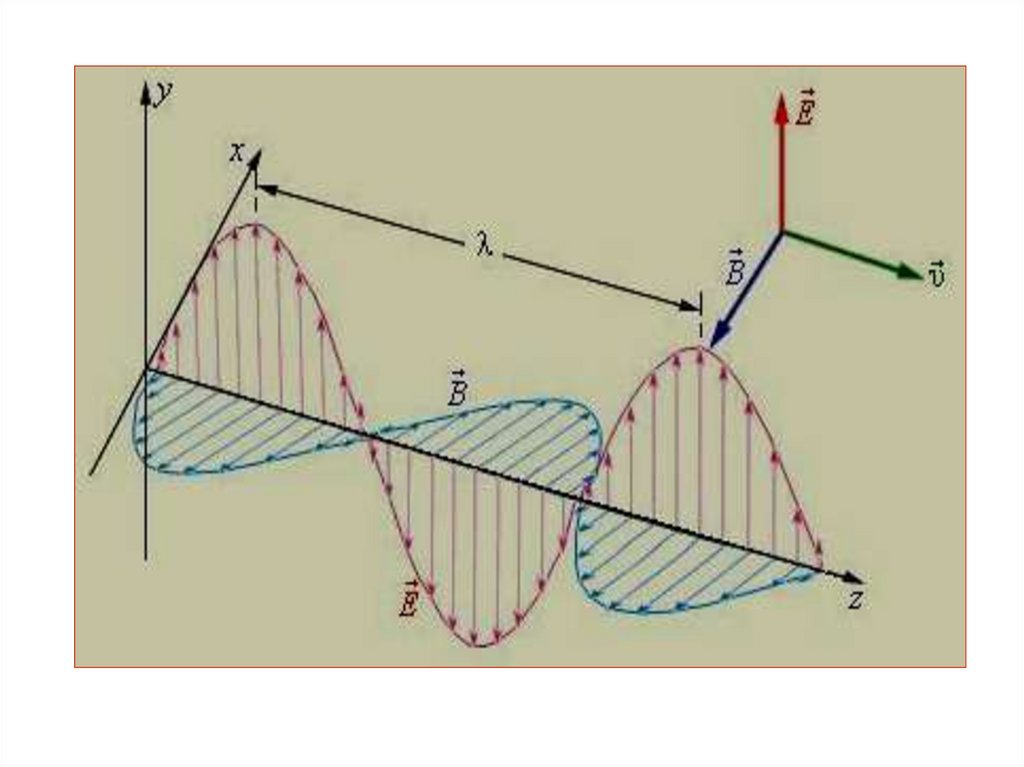
Уравнения плоской электромагнитной волны, распространяющейся в направлении Х:E y E m cos( t kx )
H z H m cos( t kx )
Умножим Ey на j , а Hz на k.
E E m cos( t kx )
H H m cos( t kx )
35.
В электромагнитной волне происходят взаимные превращенияэлектрического и магнитного полей. Электромагнитные волны
переносят энергию. При распространении волн возникает поток
электромагнитной энергии.
Рассмотрим электромагнитную волну, распространяющуюся в
вакууме:
0E 2 0H 2
- плотность энергии (для вакуума)
w wэ wм
2
2
В каждый момент времени wэ = wм (для вакуума и непроводящей среды).
36.
Вектор плотности потока энергии - вектор Пойнтинга:S [ E, H ]
S E H w c - для вакуума
37.
Из теории Максвелла следовало, что электромагнитные волны должныоказывать давление на поглощающее или отражающее тело. Давление
электромагнитного излучения объясняется тем, что под действием
электрического поля волны в веществе возникают слабые токи, то есть
упорядоченное движение заряженных частиц. На эти токи действует сила
Ампера со стороны магнитного поля волны, направленная в толщу
вещества. Эта сила и создает результирующее давление.
Первые эксперименты по определению давления излучения на отражающие
и поглощающие тела были выполнены П. Н. Лебедевым (1900 г.).
38.
Электромагнитные волны могут возбуждаться только ускореннодвижущимися зарядами. Простейшей системой, излучающей
электромагнитные волны, является небольшой по размерам
электрический диполь, дипольный момент которого изменяется
во времени. Такой диполь называют диполем Герца.































 physics
physics








