Решение задач с помощью графов

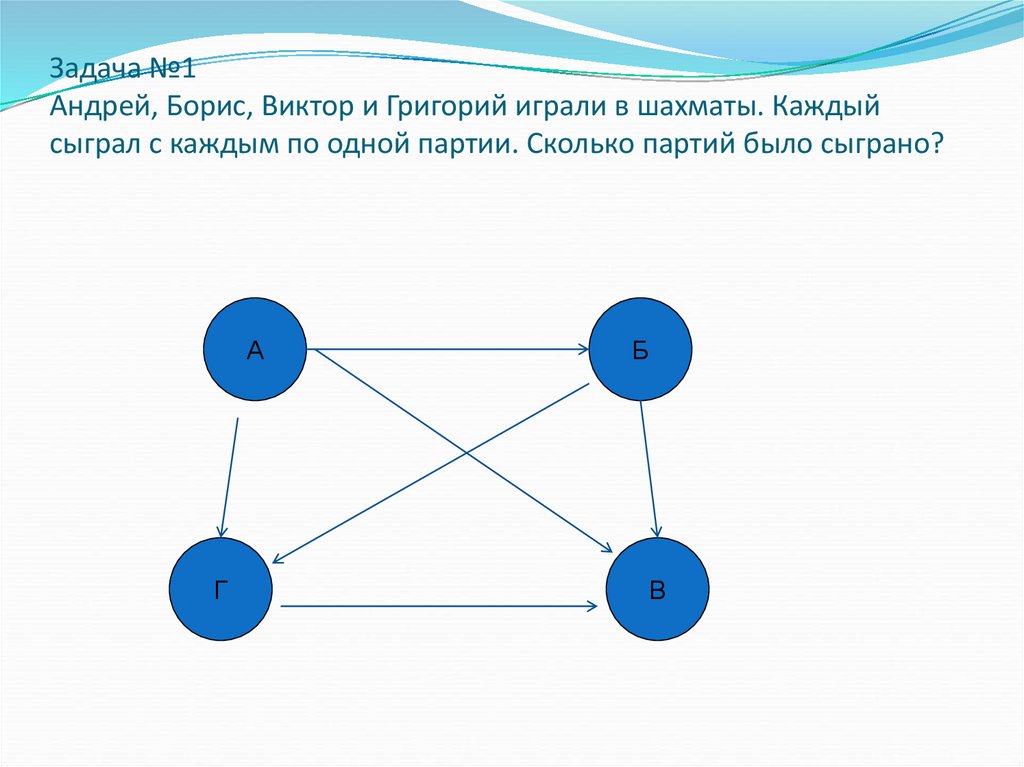
1. Задача №1 Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было

сыграно?
А
Г
Б
В

2. Тема урока: «Решение задач с помощью графов»

3. Вопросы к уроку.

Чем занимается комбинаторика?
Что такое граф?
Какие задачи относятся к комбинаторным?
Как решаются комбинаторные задачи с помощью
графов?

4. 1.Чем занимается комбинаторика?

Комбинаторика-раздел математики
,рассматривающий вопросы(задачи), связанные с
подсчётом числа всевозможных комбинаций из
элементов данного конечного множества при
сделанных исходных предположениях.

5. Что такое комбинаторика?

Комбинаторика – раздел математики, в
котором изучаются вопросы о том, сколько
различных комбинаций, подчиненных тем или иным
условиям, можно составить из заданных объектов.
Слово «комбинаторика» происходит от
латинского слова «combinare», что в переводе на
русский означает – «сочетать», «соединять».
Термин "комбинаторика" был введён
знаменитым Готфридом Вильгельмом Лейбницем, всемирно известным немецким учёным.
Комбинаторика - важный раздел математики,
знание которого необходимо представителям самых
разных специальностей. С комбинаторными
задачами приходится иметь дело физикам, химикам,
биологам, лингвистам, специалистам по кодам и др.
Комбинаторные методы лежат в основе решения многих задач теории
вероятностей и ее приложений.

6. 2.Что такое граф?

Граф-геометрическая фигура,состоящая из
точек(вершины графа) и линий,их
соединяющих(рёбра графа).

7. Примеры графов.

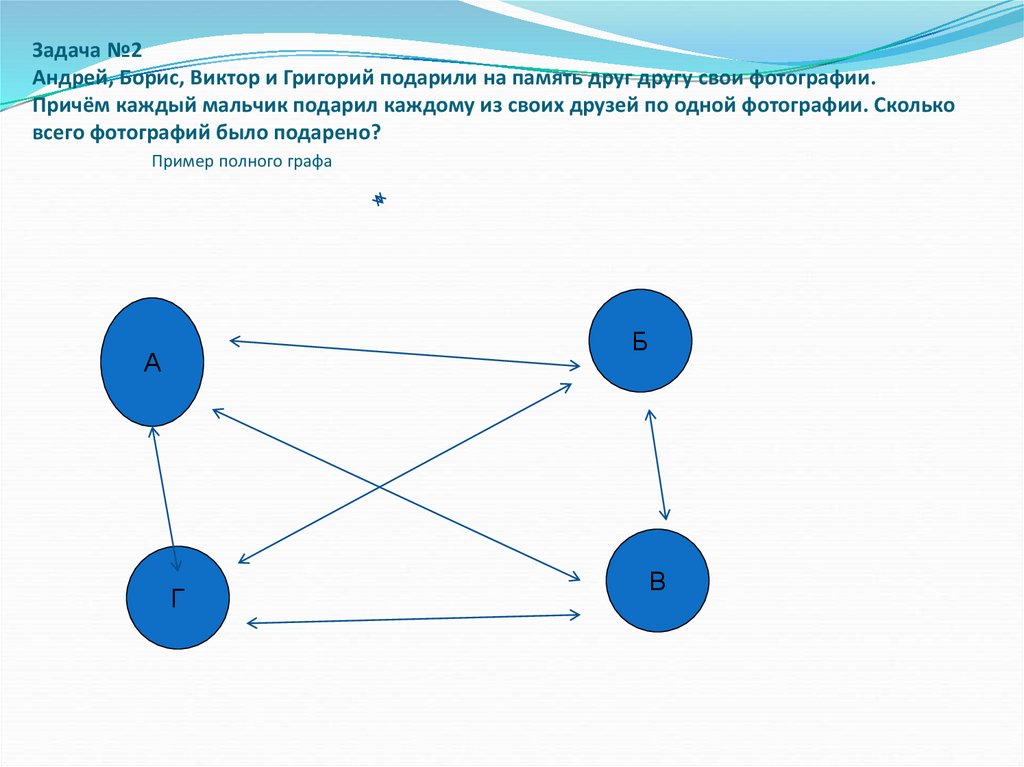
8. Задача №2 Андрей, Борис, Виктор и Григорий подарили на память друг другу свои фотографии. Причём каждый мальчик подарил каждому

из своих друзей по одной фотографии. Сколько
всего фотографий было подарено?
Пример полного графа
Б
А
Г
В

9. II способ

Каждый из 4 мальчиков
подарил друзьям 3
фотографии, следовательно,
всего было подарено 3*4=12
фотографий.
.

10. Примеры графов

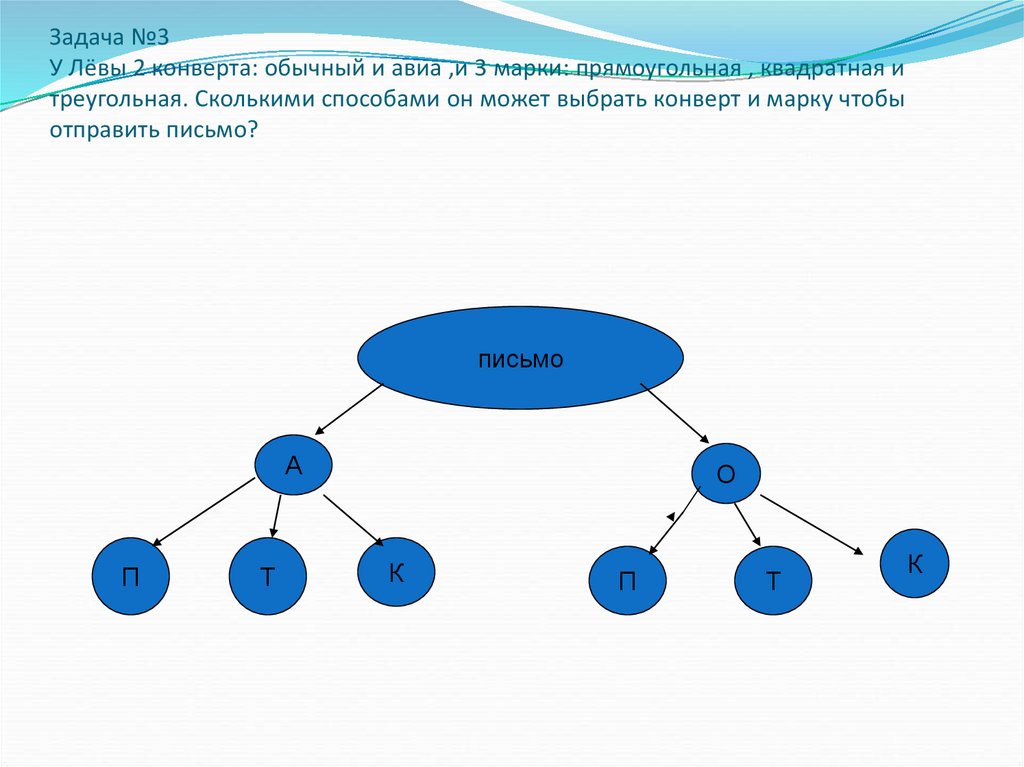
11. Задача №3 У Лёвы 2 конверта: обычный и авиа ,и 3 марки: прямоугольная , квадратная и треугольная. Сколькими способами он может

выбрать конверт и марку чтобы
отправить письмо?
письмо
А
П
Т
О
К
П
Т
К

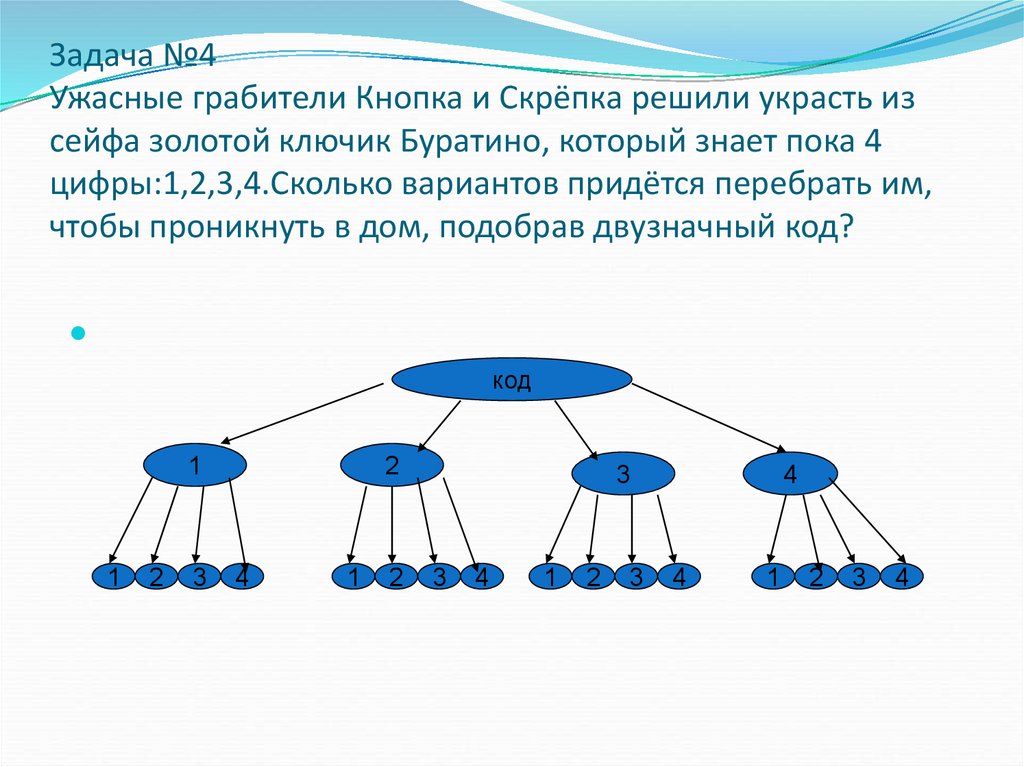
12. Задача №4 Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4

цифры:1,2,3,4.Сколько вариантов придётся перебрать им,
чтобы проникнуть в дом, подобрав двузначный код?
код
1
1
2
3
2
4
1
2
3
3
4
1
2
3
4
4
1
2
3
4

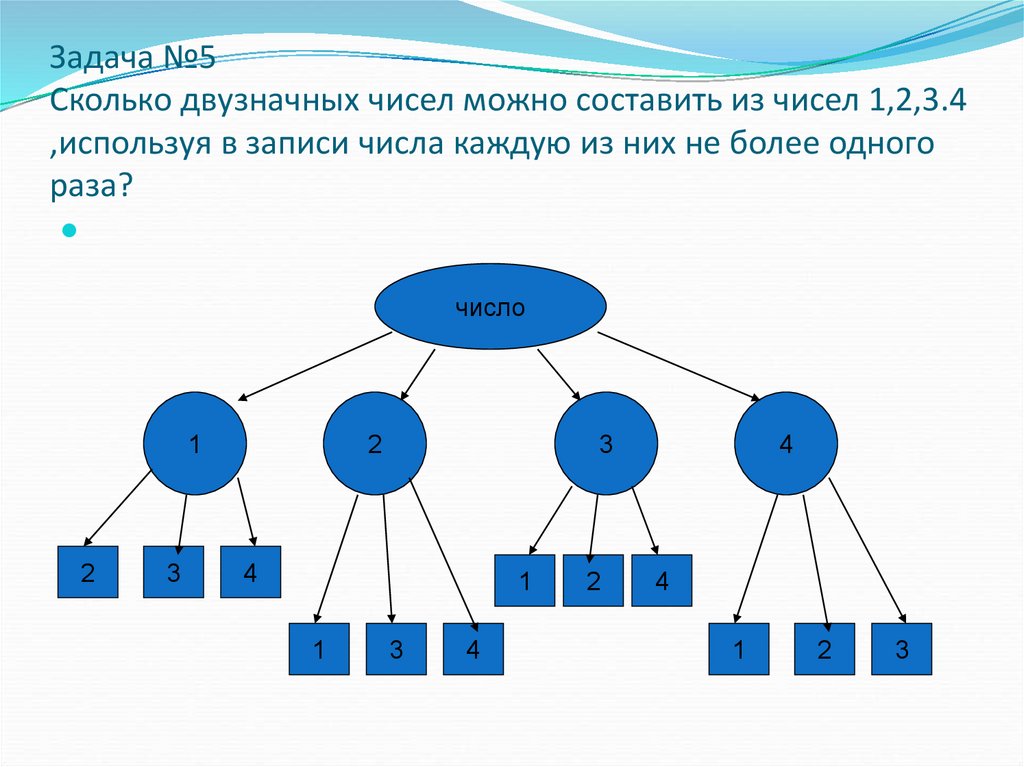
13. Задача №5 Сколько двузначных чисел можно составить из чисел 1,2,3.4 ,используя в записи числа каждую из них не более одного

раза?
число
1
2
3
2
3
4
1
1
3
4
2
4
4
1
2
3

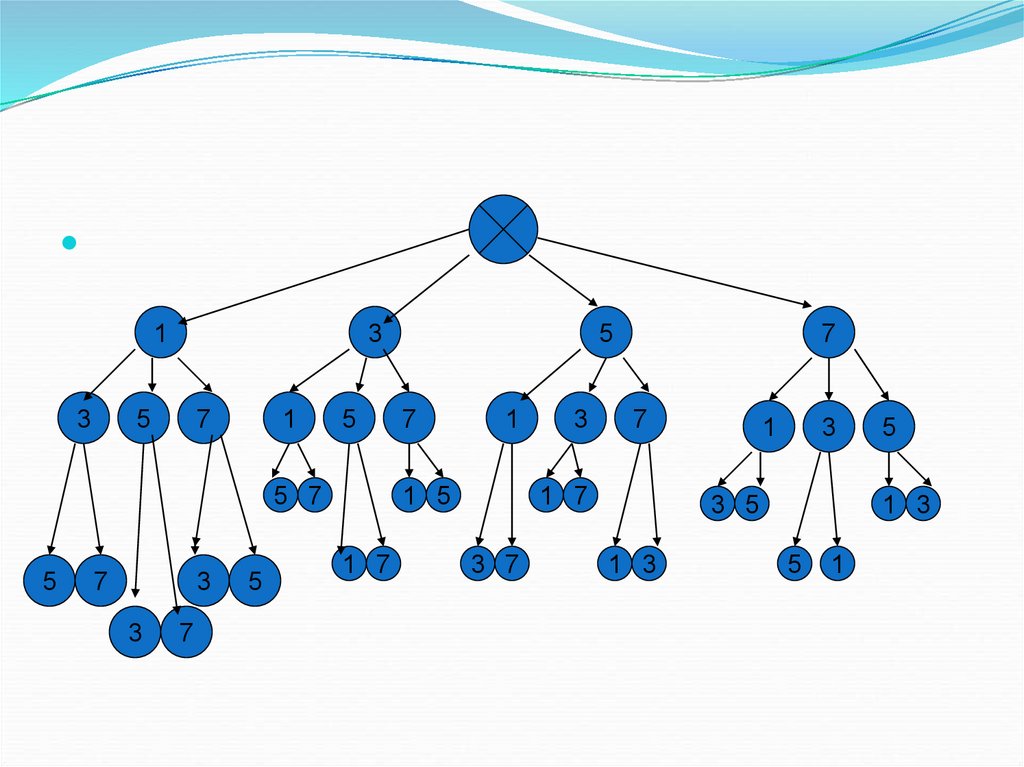
14. Задача №6 Сколько трёхзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного

раза?

15.

1
3
5
5
7
3
7
1
5
5
7
1
3
7
7
1
3
5

16.

1
3
3
5
7
1
5
5 7
5
7
3
3
7
5
5
7
1
1 5
1 7
3
7
7
1 7
3 7
1
3
3 5
1 3
5
1 3
5
1

17. 4*3*2=24

Первую цифру трёхзначного числа
можно выбрать четырьмя
способами. Так как после выбора
первой цифры останутся три, то
вторую цифру, из оставшихся, можно
выбрать тремя способами. Наконец
третью цифру можно выбрать, из
оставшихся, двумя способами.

18. Задача №7 Сколько трёхзначных чисел можно записать из цифр 1,2,3 при условии, что 1)цифры в записи числа должны быть различны;

Сколько трёхзначных чисел
можно записать из цифр 1,2,3
при условии, что 1)цифры в
записи числа должны быть
различны;
2)цифры в записи числа могут
повторяться?

19. Задача №8 (устно) Сколькими способами Петя и Вова могут занять места за двухместной партой?

Задача №8 (устно)
Сколькими способами Петя и Вова могут занять
за двухместной партой?
места
Сколькими способами вы можете
рассадить 3-х гостей на 3-х разноцветных
табуретках.
№. Сколькими способами вы можете
рассадить 4-х гостей на 4-х разноцветных
табуретках?
№.Сколькими способами вы можете
рассадить 5-х гостей на 5-х разноцветных
табуретках?

20. «Правило произведения».

Если существует n вариантов выбора
первого элемента и для каждого из
них есть m вариантов выбора
второго элемента,то всего
существует nxm различных пар с
выбранными первым и вторым
элементами.

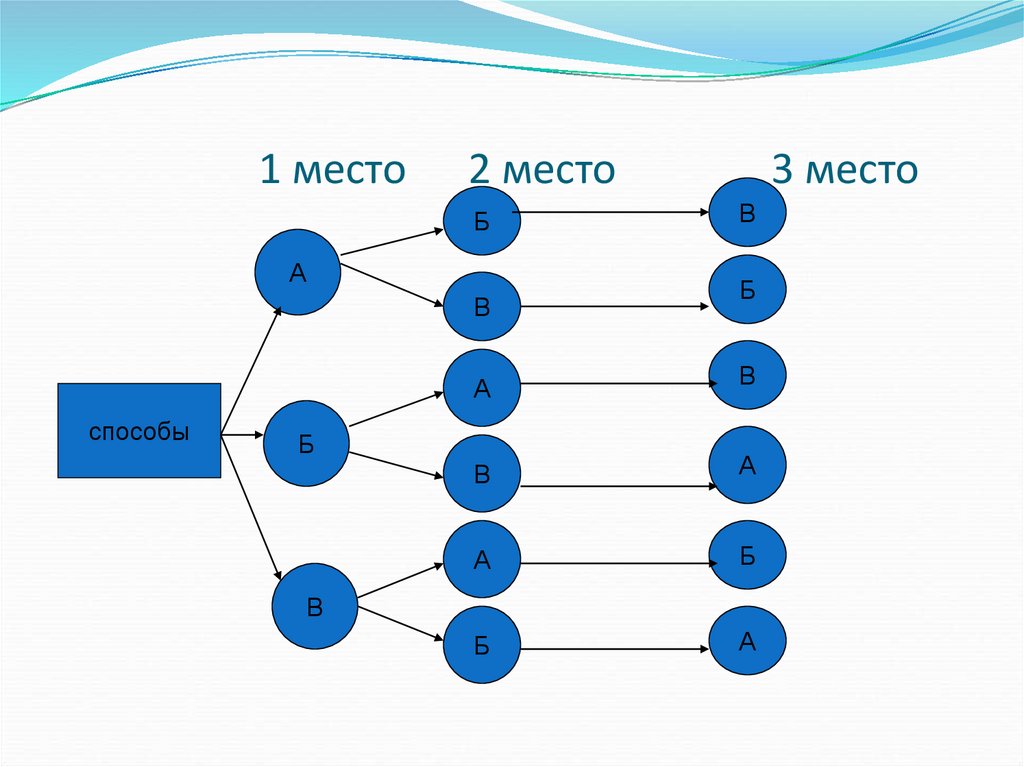
21. Задача № 9

№.Антон, Борис и Василий купили 3
билета на 1-е,2-е и 3-е места первого
ряда на футбольный матч.
Сколькими способами они могут
занять имеющиеся места?

22. 1 место 2 место 3 место

1 место
2 место
Б
А
В
способы
3 место
В
Б
А
В
В
А
А
Б
Б
А
Б
В

23. Задача №10

№.В пятницу у вас 4 уроков: алгебра,
русский, физика, история.
Сколькими способами можно
составить расписание на пятницу?

24.

25. Задание на дом

Подготовьте материал по темам:
История возникновения комбинаторики и этапы
её развития
. Учёные, внёсшие вклад в развитие
комбинаторики.
Проблемы комбинаторики.
История возникновения теории графов.
Терминология теории графов. Некоторые задачи
теории графов.

26. Решите задачи:

1. Сколько различных трёхзначных чисел
можно записать с помощью цифр:1)1 и 2;2)0 и 1?
2. Сколько различных трёхзначных чисел
можно записать с помощью цифр 5,6,7,8,9,если:
1) цифры в числе могут повторяться;
2) цифры в числе должны быть различны?