Similar presentations:
Теория графов в задачах
1. Тема проекта: «Теория графов в задачах»
2. Актуальность
В настоящее время теория графов стала оченьпопулярной среди учителей, школьников и
студентов. Это связано с тем, что при помощи этой
теории можно довольно просто решать круг
разнообразных задач. Я решил узнать, как можно
применить теорию графов на практике и получить
возможность минимизировать временные затраты и
оптимизировать способы решения задач.
3. исследовать эффективность использования теории графов при решении задач.
Цель:исследовать эффективность использования
теории
графов
при
решении
задач.
Задачи:
1. Изучить научную литературу о теории
графов.
2. Исследовать задачи по математике и
информатике, решаемые с помощью графов.
3. Продемонстрировать исследованные задачи
на предметной неделе.
4. Методы:
Теоретический - изучение теоретическогоматериала по теме;
Исследовательский - осмысление, научное
познание;
Рефлексии
- погружение в себя и
самопознание;
Описания - представление использования
метода графов на практике.
5. как научиться эффективно использовать теорию графов при решении задач
Проблема:как научиться эффективно использовать теорию
графов при решении задач
Гипотеза:
Если теорию графов правильно применять при
решении задач, то можно значительно сократить
затраты времени на их решение
.
6. Предмет исследования: Теория графов
Объект исследования:задачи, решаемые с помощью
графов
7. История возникновения теории графов
ЛеонардЭйлер
(1707 – 1783)
8.
Теория графов - раздел дискретнойматематики,
рассматривающий
множества с заданными на них
отношениями между элементами.
Граф - информационная модель,
представленная в графической форме.
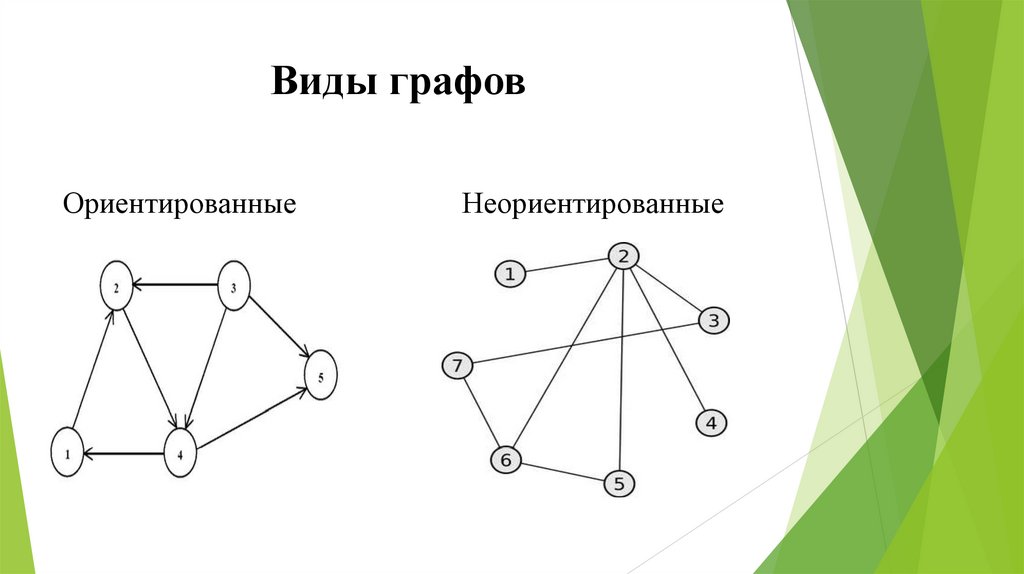
9. Виды графов
ОриентированныеНеориентированные
10. Сколько различных четырёхзначных чисел, в которых цифры не повторяются, можно составить из 0, 2, 4, 6?
Задача №11 способ решения
Сколько различных четырёхзначных чисел, в
которых цифры не повторяются, можно составить
из 0, 2, 4, 6?
11. Задача №1 2 способ решения
Сколько различных четырёхзначных чисел, вкоторых цифры не повторяются, можно составить
из 0, 2, 4, 6?
Решение:
Р₄=4!
Р₃=3!
Р₄ - Р₃ = 4! – 3! = 24 – 6 = 18
12. Задача №2
В государстве Морляндия 17 островов, между ними проложенымаршруты так, что с каждого острова выходит ровно четыре
маршрута. Докажите, что в Морляндии есть такие два острова,
что с одного до другого можно добраться двумя разными путями
(но, может быть, с пересадками на других островах).
13. Задача №2
В государстве Морляндия 17 островов, между ними проложенымаршруты так, что с каждого острова выходит ровно четыре
маршрута. Докажите, что в Морляндии есть такие два острова, что с
одного до другого можно добраться двумя разными путями (но, может
быть, с пересадками на других островах).
Решение:
1) 17·4= 68(сумма степеней вершин)
2) 68:2=34 (ребра)
14. Выводы:
графыиспользуются для наглядного представления
объектов и связи между ними;
использование теории графов делает решение многих
логических, вероятностных и комбинаторных задач
менее трудоемким;
если теорию графов правильно применять при
решении задач, то можно значительно сократить
затраты времени на их решение.
15. Заключение
Изучена теория графов и применена прирешении задач по теории вероятности,
комбинаторике, информатике и олимпиадных
задачах. Приобретен опыт решения задач
способом, который не изучается в школьной
программе.
Цель
достигнута,
гипотеза
подтверждена.













 mathematics
mathematics








