Комбинаторика. 5 класс

1. КОМБИНАТОРИКА 5 КЛАСС

• УЧИТЕЛЬ МАТЕМАТИКИ
• Сош№5 Г .МЫТИЩИ
• БУРОВА ЮЛИЯ
ВИКТОРОВНА

2. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой

ширины разных цветов
– белого, синего, красного. Сколько стран могут
использовать такую символику при условии, что у каждой
страны – свой флаг?
Предположим, что первая полоса – белая.
Тогда вторая полоса может быть синей или красной,
третья полоса соответственно, красной или синей.
Получилось два варианта: белая, синяя, красная или
белая, красная, синяя.

3. Рассмотрим следующий вариант

Предположим, что первая полоса – синяя.
Тогда вторая полоса может быть белой или красной,
третья полоса ,соответственно, красной или белой.
И,наконец, последний вариант

4. Итого

РОССИЯ
Итого

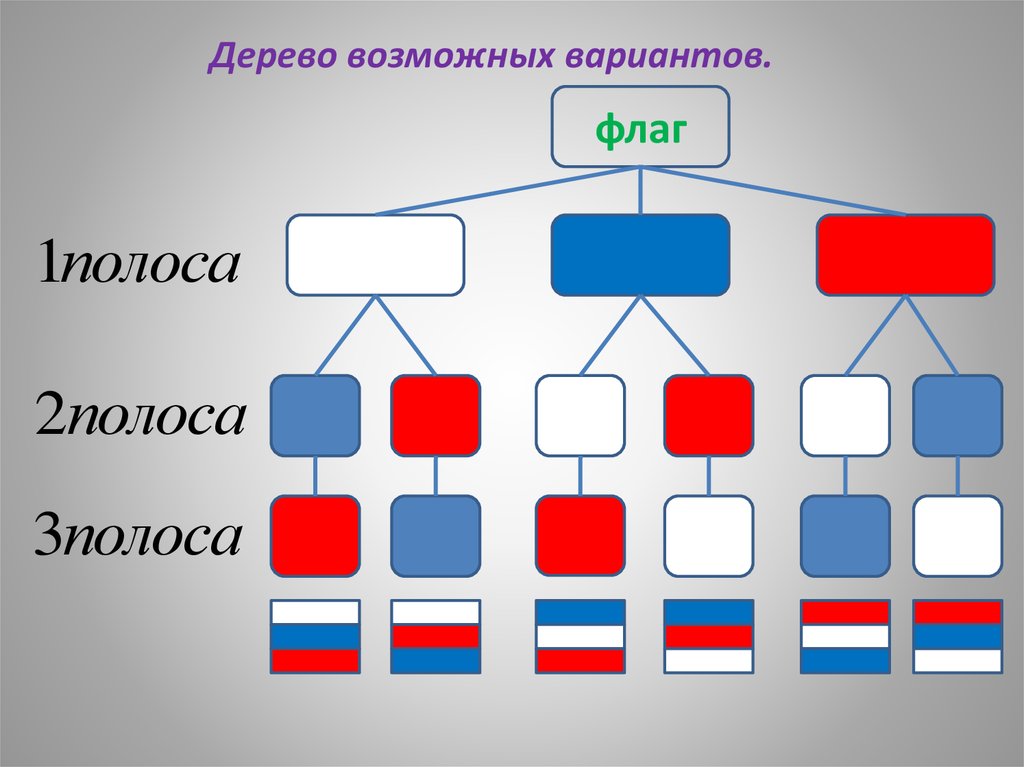
5. Дерево возможных вариантов.

флаг
1полоса
2полоса
3полоса

6.

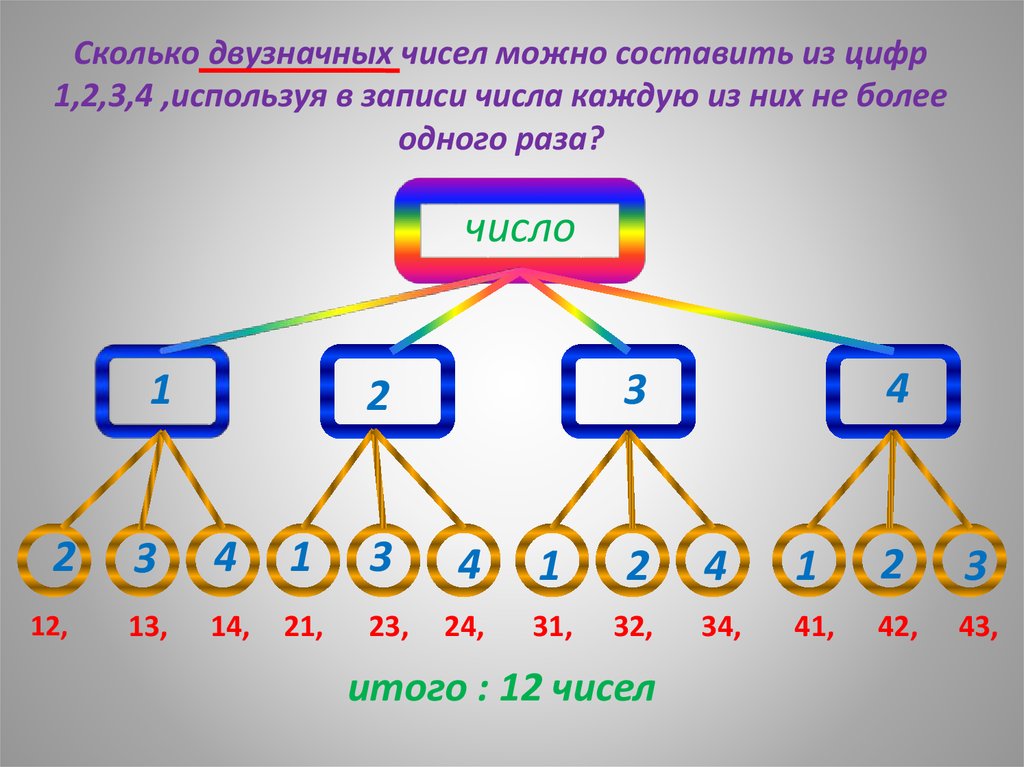
7. Сколько двузначных чисел можно составить из цифр 1,2,3,4 ,используя в записи числа каждую из них не более одного раза?

число
1
2
12,
4
3
2
3
4
1
3
4
1
2
4
1
2
3
13,
14,
21,
23,
24,
31,
32,
34,
41,
42,
43,
итого : 12 чисел

8.

• Итак, при решении этой задачи мы
использовали 2 способа :
• 1)способ перебора возможных
вариантов.
• 2)Построение дерева возможных
• вариантов

9.

Пример.
1 ?3 3
?
111
112
113
121
122
123
131
132
133
9 вариантов

10.

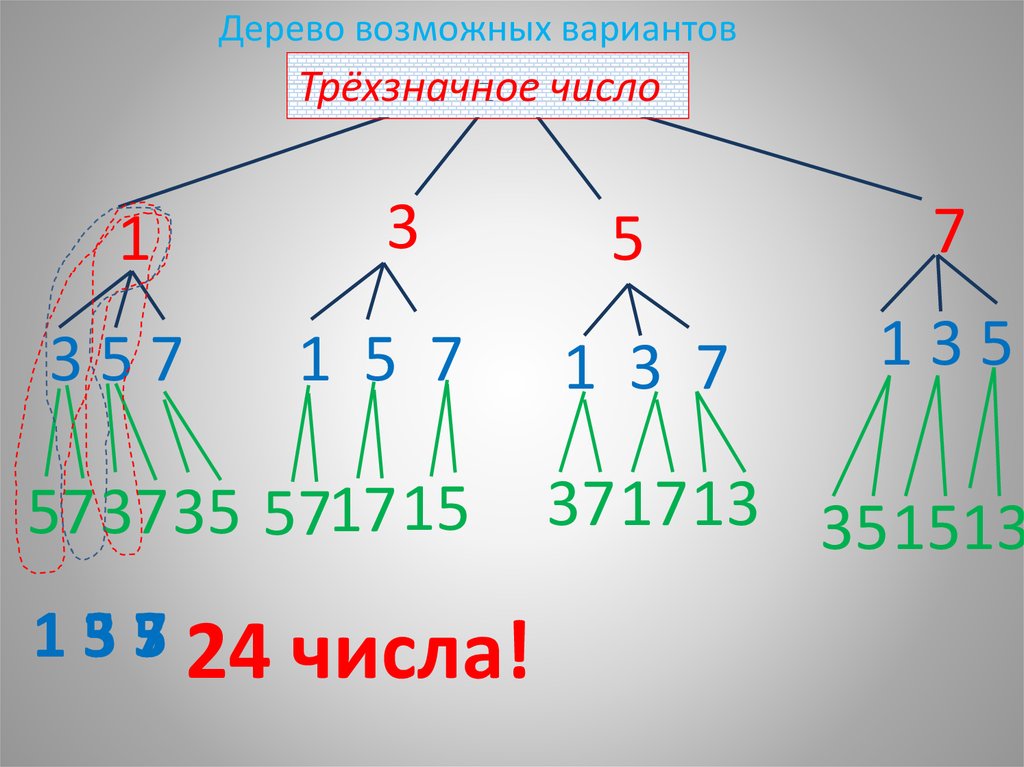
Пример
Сколько трёхзначных чисел
можно составить из цифр
1, 3, 5,
7,
используя в записи числа
каждую из них не более
одного раза?

11.

Перебором:
135 137 153
157
173 175
315 317 351
357
371 375
513 517 531
537
571 573
713 715
735 751 753
731

12.

Дерево возможных вариантов
Трёхзначное число
1
357
3
1 5 7
5737 35 5717 15
15
33
5
7 24 числа!
5
7
1 3 7
135
371713 351513

13.

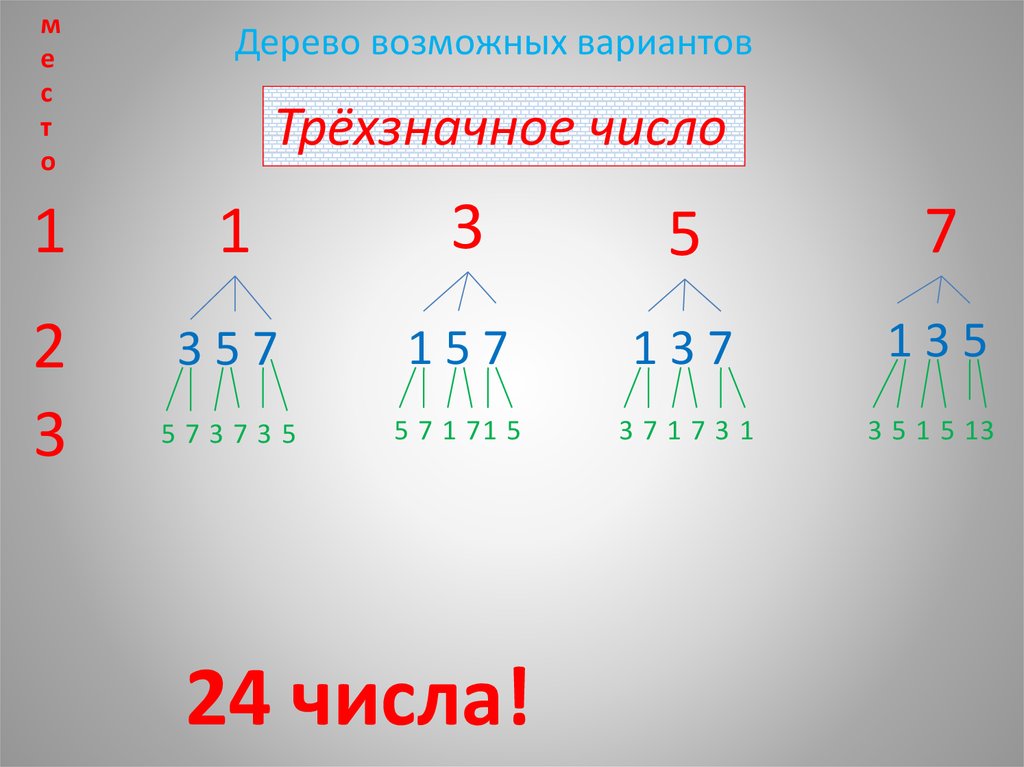
м
е
с
т
о
Дерево возможных вариантов
Трёхзначное число
1
1
3
5
7
2
3
357
157
137
135
573735
5 7 1 71 5
371731
3 5 1 5 13
24 числа!

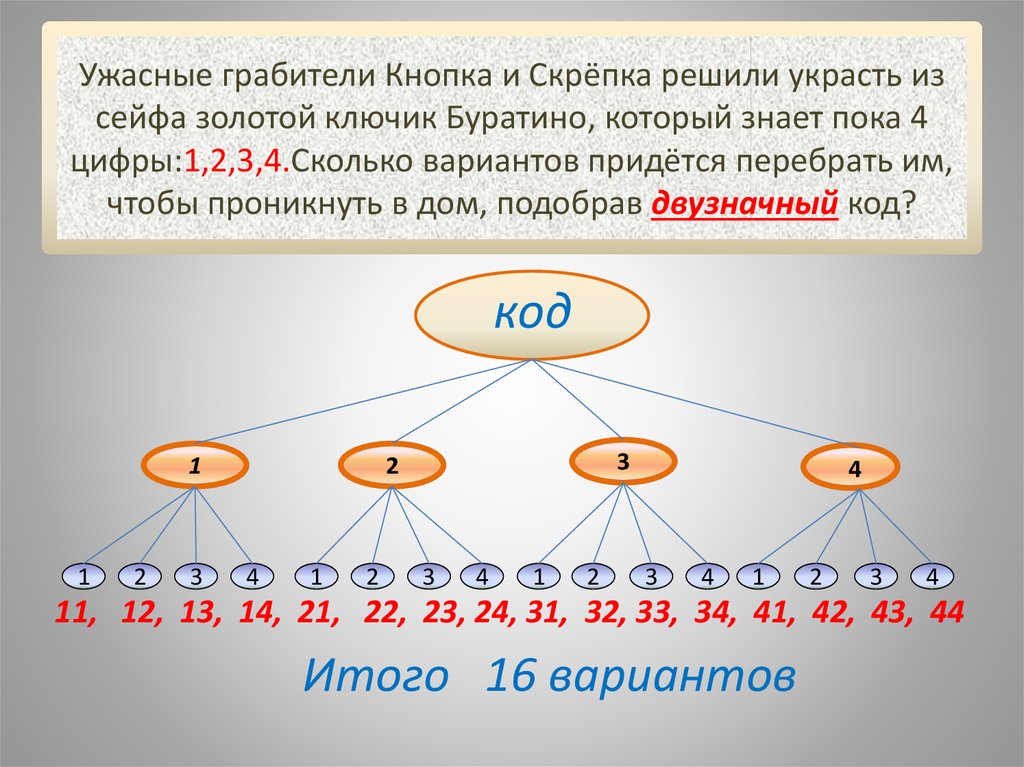
14. Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько

вариантов придётся перебрать им,
чтобы проникнуть в дом, подобрав двузначный код?
код
1
1
2
3
3
2
4
1
2
3
4
1
2
4
3
4
1
2
3
4
11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44
Итого 16 вариантов

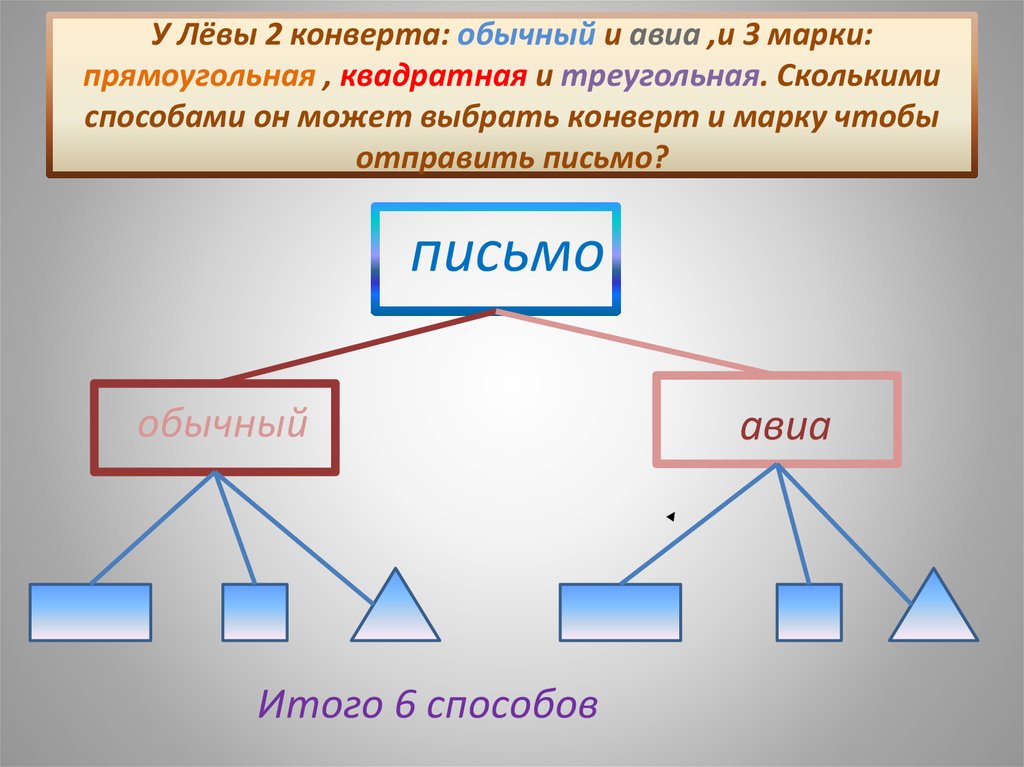
15. У Лёвы 2 конверта: обычный и авиа ,и 3 марки: прямоугольная , квадратная и треугольная. Сколькими способами он может выбрать

конверт и марку чтобы
отправить письмо?
письмо
обычный
Итого 6 способов
авиа

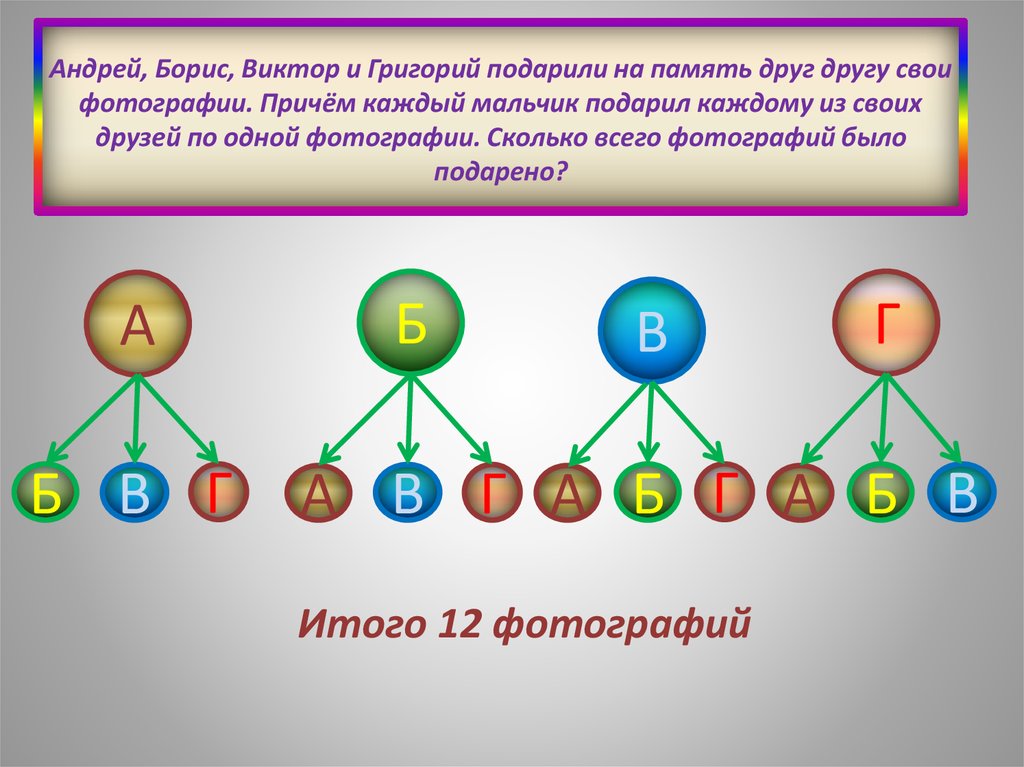
16. Андрей, Борис, Виктор и Григорий подарили на память друг другу свои фотографии. Причём каждый мальчик подарил каждому из своих

друзей по одной фотографии.
Сколько всего фотографий было подарено?
А
Б
В
Г
Итого 12 фотографий

17. Андрей, Борис, Виктор и Григорий подарили на память друг другу свои фотографии. Причём каждый мальчик подарил каждому из своих

друзей по одной фотографии. Сколько всего фотографий было
подарено?
А
Б В Г
Б
В
Г
А В Г А Б Г А Б В
Итого 12 фотографий

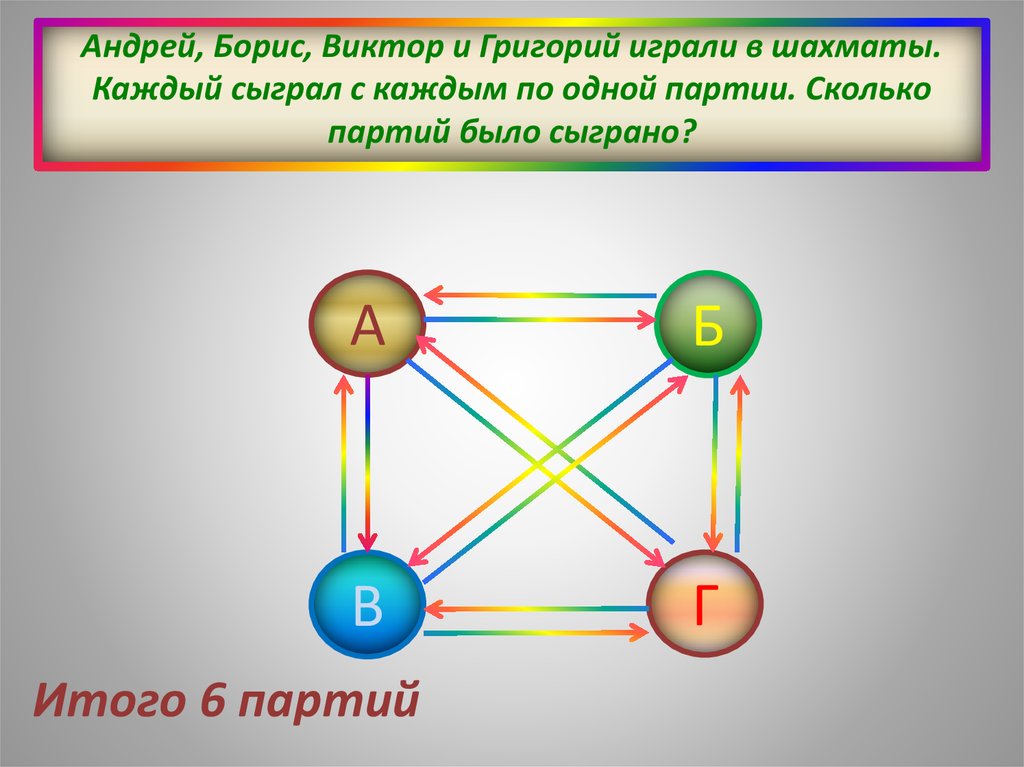
18. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

А
Б
В
Г
Итого 6 партий

19. Задача №

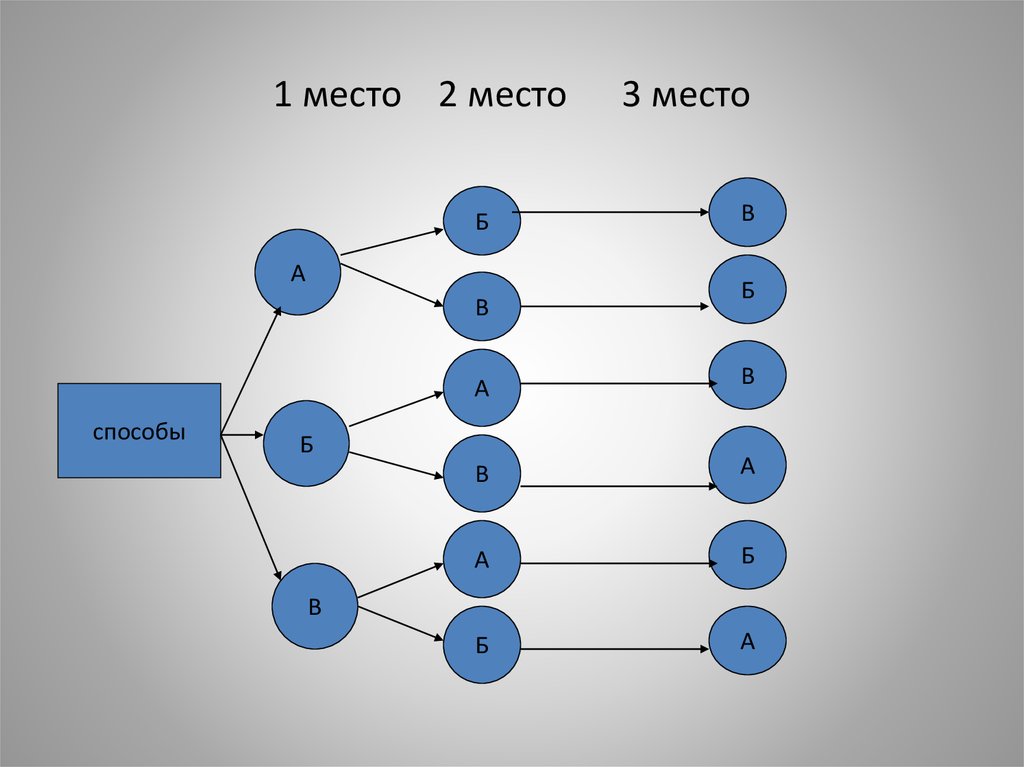
• №.Антон, Борис и Василий купили 3 билета
на 1-е,2-е и 3-е места первого ряда на
футбольный матч. Сколькими способами
они могут занять имеющиеся места?

20. 1 место 2 место 3 место

1 место 2 место
Б
А
В
способы
3 место
В
Б
А
В
В
А
А
Б
Б
А
Б
В

21. Задача №(устно) Сколькими способами Петя и Вова могут занять места за двухместной партой?

Задача №(устно)
Сколькими способами Петя и Вова могут занять
двухместной партой?
места за
• Сколькими способами вы можете рассадить
3-х гостей на 3-х разноцветных табуретках.
• №. Сколькими способами вы можете
рассадить 4-х гостей на 4-х разноцветных
табуретках?
• №.Сколькими способами вы можете
рассадить 5-х гостей на 5-х разноцветных
табуретках?

22. Задача №

• №.В пятницу у вас 4 уроков: алгебра,
русский, физика, история. Сколькими
способами можно составить расписание на
пятницу?

23. Задача.

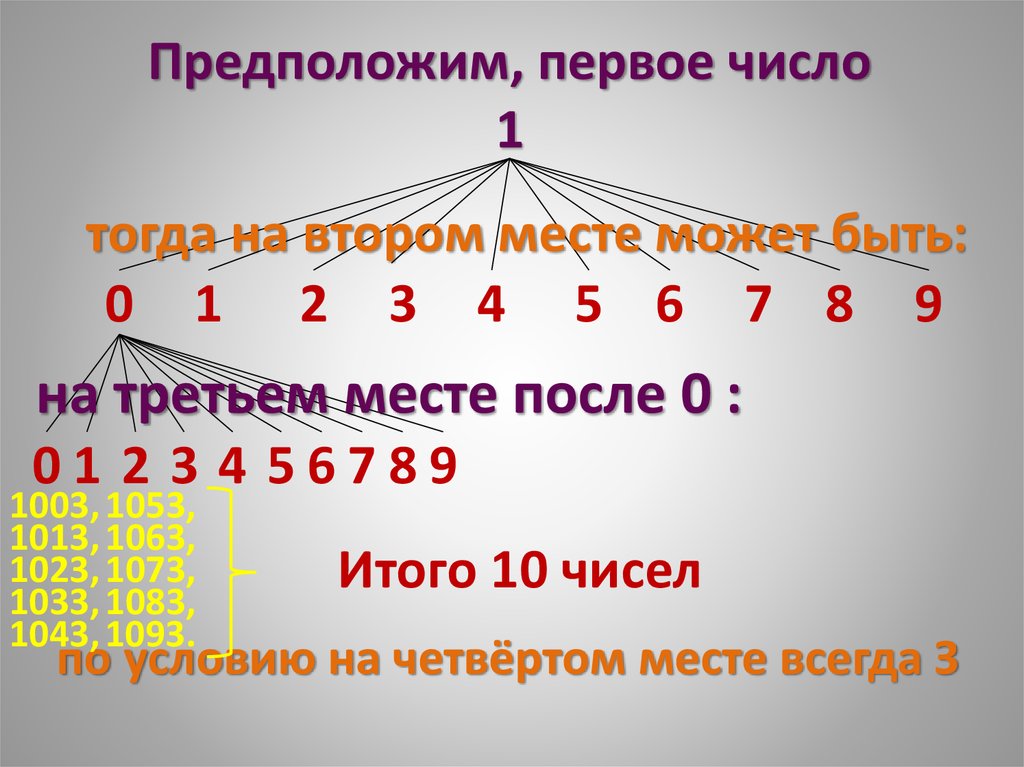
• Сколько всего
четырёхзначных чисел ,
оканчивающихся цифрой 3 ?

24. Предположим, первое число 1

тогда на втором месте может быть:
0 1 2 3 4 5 6 7 8 9
на третьем месте после 0 :
01 2 3 4 56789
1003, 1053,
1013, 1063,
1023, 1073,
1033, 1083,
1043, 1093.
Итого 10 чисел
по условию на четвёртом месте всегда З

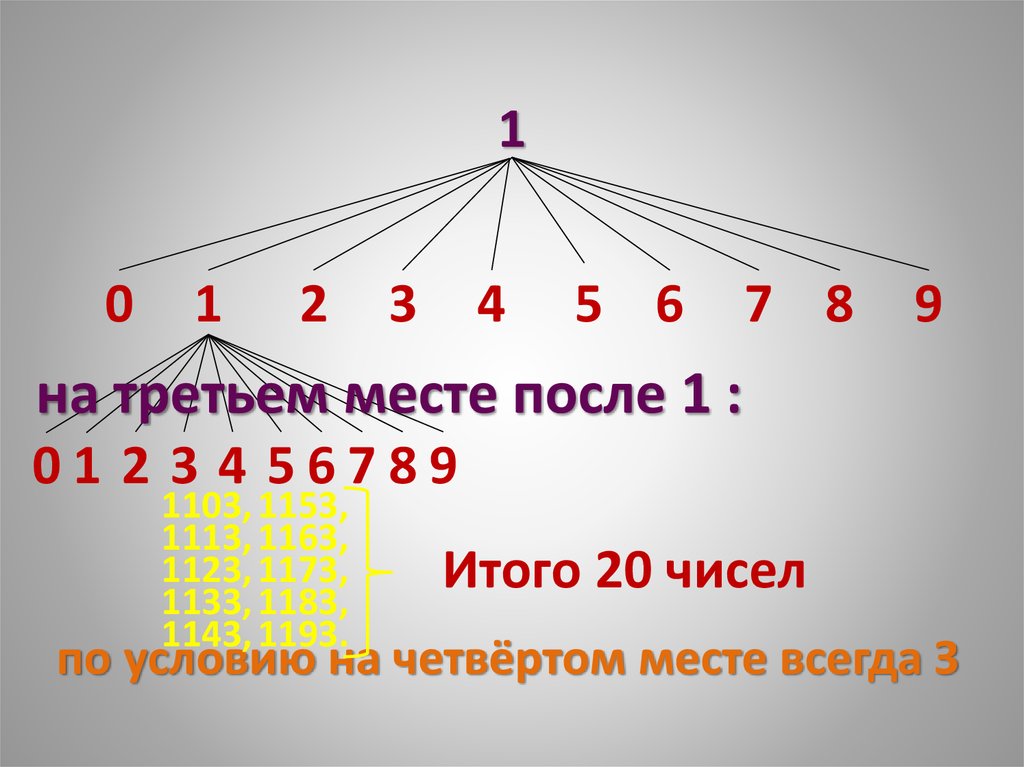
25. 1

0
1
2
3
4
5 6
7 8
9
на третьем месте после 1 :
01 2 3 4 56789
1103, 1153,
1113, 1163,
1123, 1173,
1133, 1183,
1143, 1193.
Итого 20 чисел
по условию на четвёртом месте всегда З

26. Итого:

100 х 9 = 900