Графы и их применение при решении задач

1.

2. Немного истории

Леонард Эйлер –
российский, немецкий и
швейцарский математик,
внесший огромный вклад в
развитие математики. С его
именем связана история
появления графов. Часто
упоминается его задача о
Кенигсбергских мостах.
Леонард Эйлер
(1707-1783 гг.)

3. Немного истории

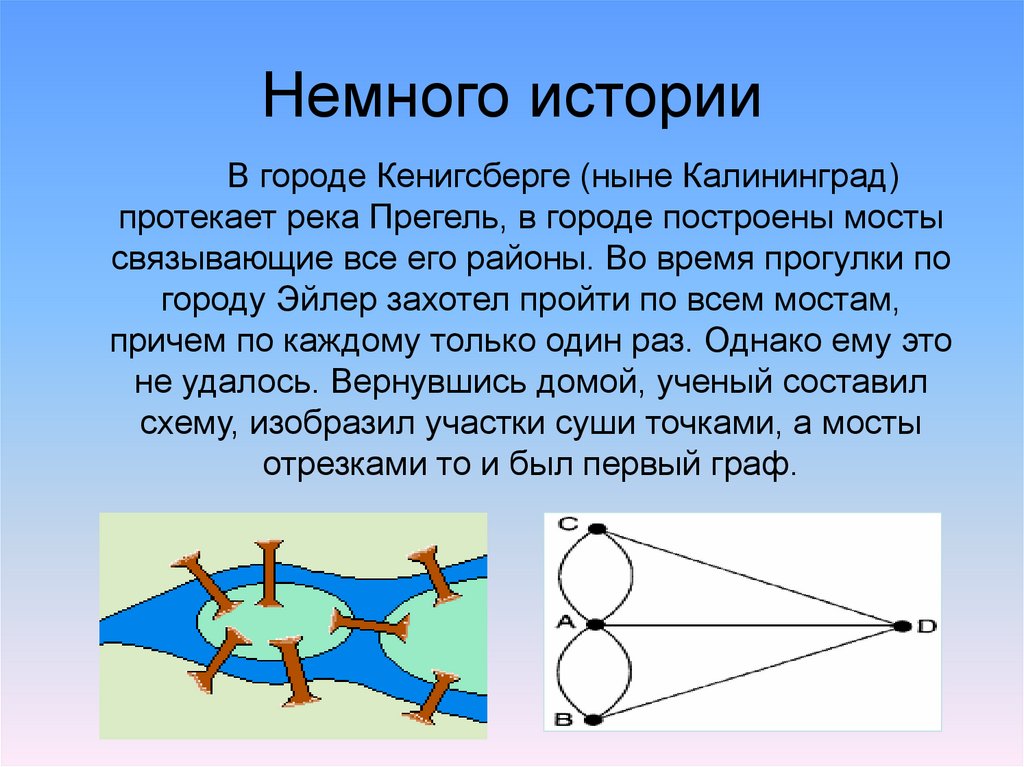
В городе Кенигсберге (ныне Калининград)
протекает река Прегель, в городе построены мосты
связывающие все его районы. Во время прогулки по
городу Эйлер захотел пройти по всем мостам,
причем по каждому только один раз. Однако ему это
не удалось. Вернувшись домой, ученый составил
схему, изобразил участки суши точками, а мосты
отрезками то и был первый граф.

4. Что такое граф?

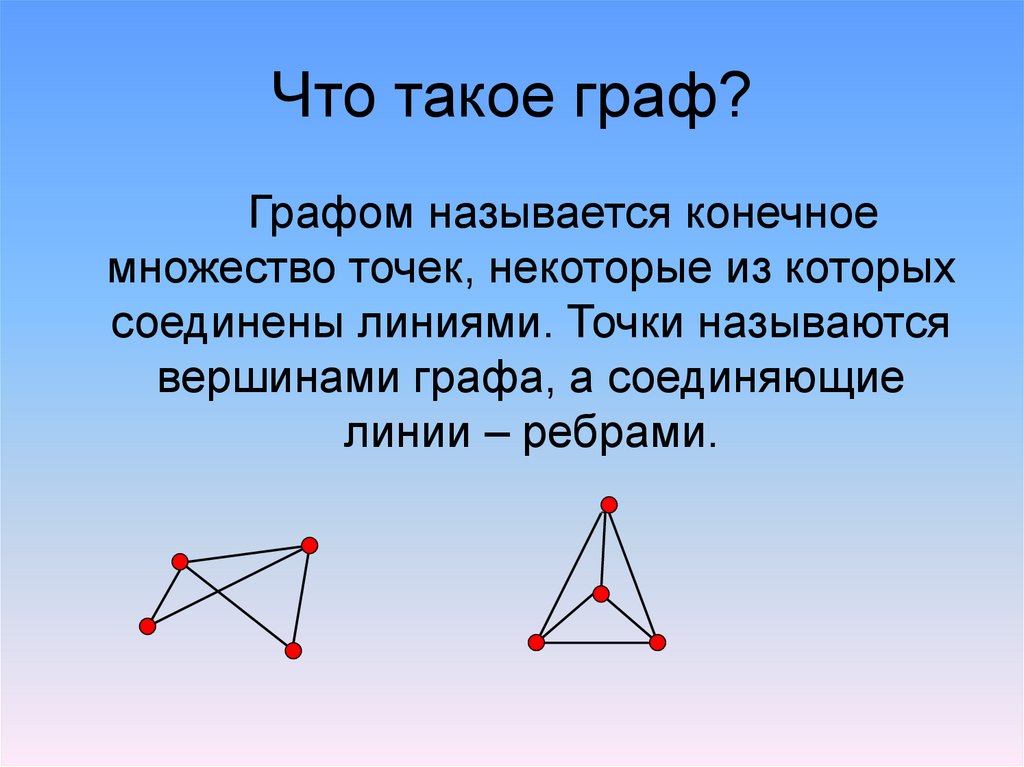
Графом называется конечное
множество точек, некоторые из которых
соединены линиями. Точки называются
вершинами графа, а соединяющие
линии – ребрами.

5. Примеры графов

6. Задача

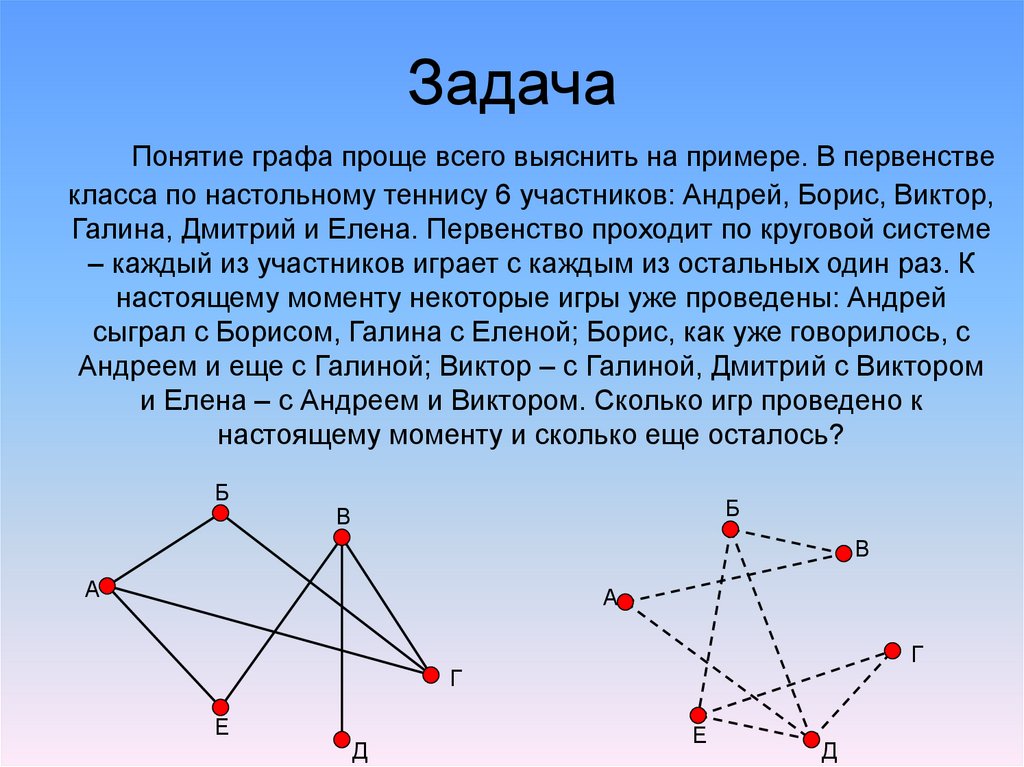
Понятие графа проще всего выяснить на примере. В первенстве
класса по настольному теннису 6 участников: Андрей, Борис, Виктор,
Галина, Дмитрий и Елена. Первенство проходит по круговой системе
– каждый из участников играет с каждым из остальных один раз. К
настоящему моменту некоторые игры уже проведены: Андрей
сыграл с Борисом, Галина с Еленой; Борис, как уже говорилось, с
Андреем и еще с Галиной; Виктор – с Галиной, Дмитрий с Виктором
и Елена – с Андреем и Виктором. Сколько игр проведено к
настоящему моменту и сколько еще осталось?
Б
Б
В
В
А
А
Г
Г
Е
Д
Е
Д

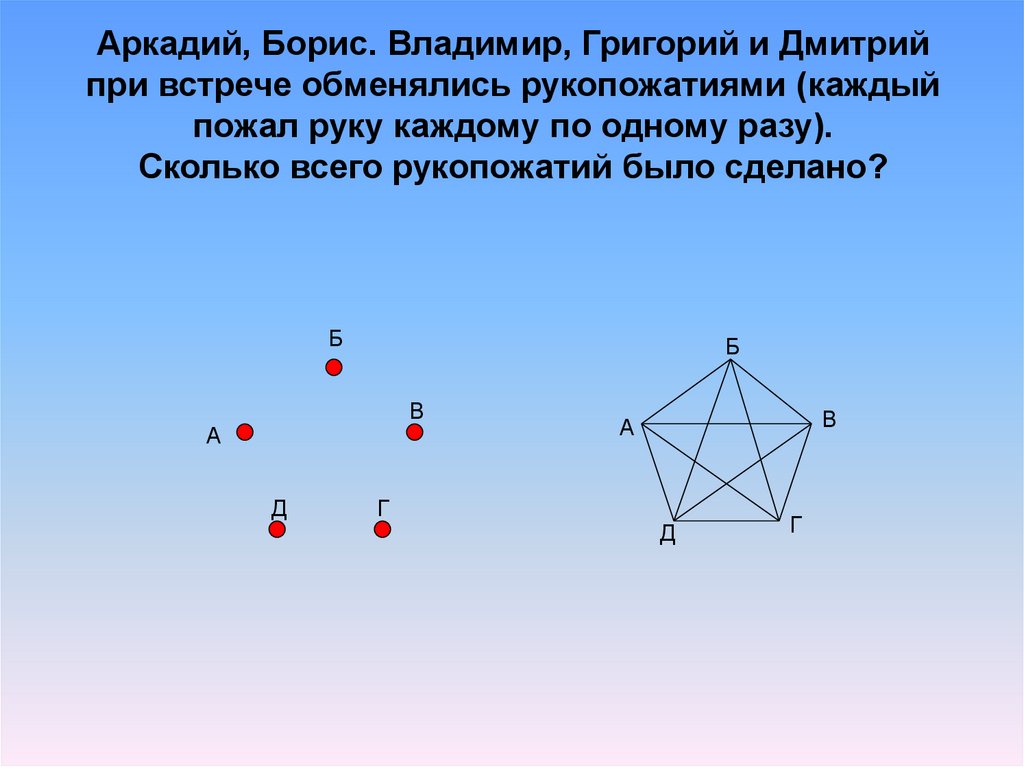
7. Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу).

Сколько всего рукопожатий было сделано?
Б
Б
В
А
Д
Г
В
А
Д
Г

8. Задача

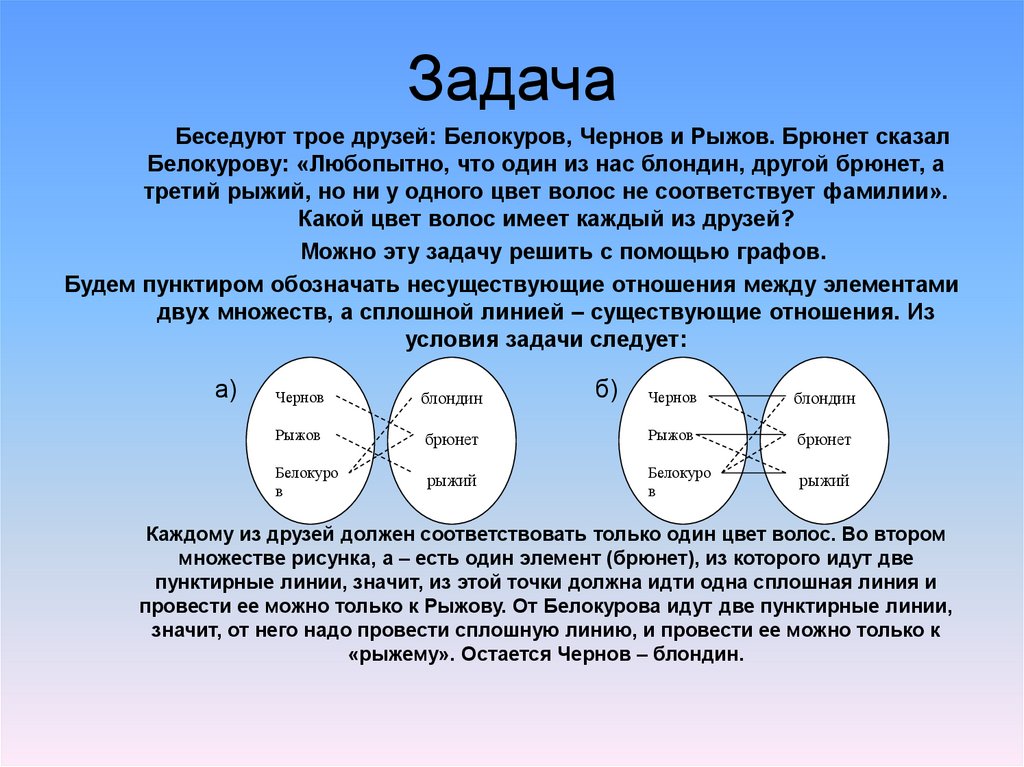
Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал
Белокурову: «Любопытно, что один из нас блондин, другой брюнет, а
третий рыжий, но ни у одного цвет волос не соответствует фамилии».
Какой цвет волос имеет каждый из друзей?
Можно эту задачу решить с помощью графов.
Будем пунктиром обозначать несуществующие отношения между элементами
двух множеств, а сплошной линией – существующие отношения. Из
условия задачи следует:
а)
Чернов
блондин
Рыжов
Белокуро
в
б)
Чернов
блондин
брюнет
Рыжов
брюнет
рыжий
Белокуро
в
рыжий
Каждому из друзей должен соответствовать только один цвет волос. Во втором
множестве рисунка, а – есть один элемент (брюнет), из которого идут две
пунктирные линии, значит, из этой точки должна идти одна сплошная линия и
провести ее можно только к Рыжову. От Белокурова идут две пунктирные линии,
значит, от него надо провести сплошную линию, и провести ее можно только к
«рыжему». Остается Чернов – блондин.

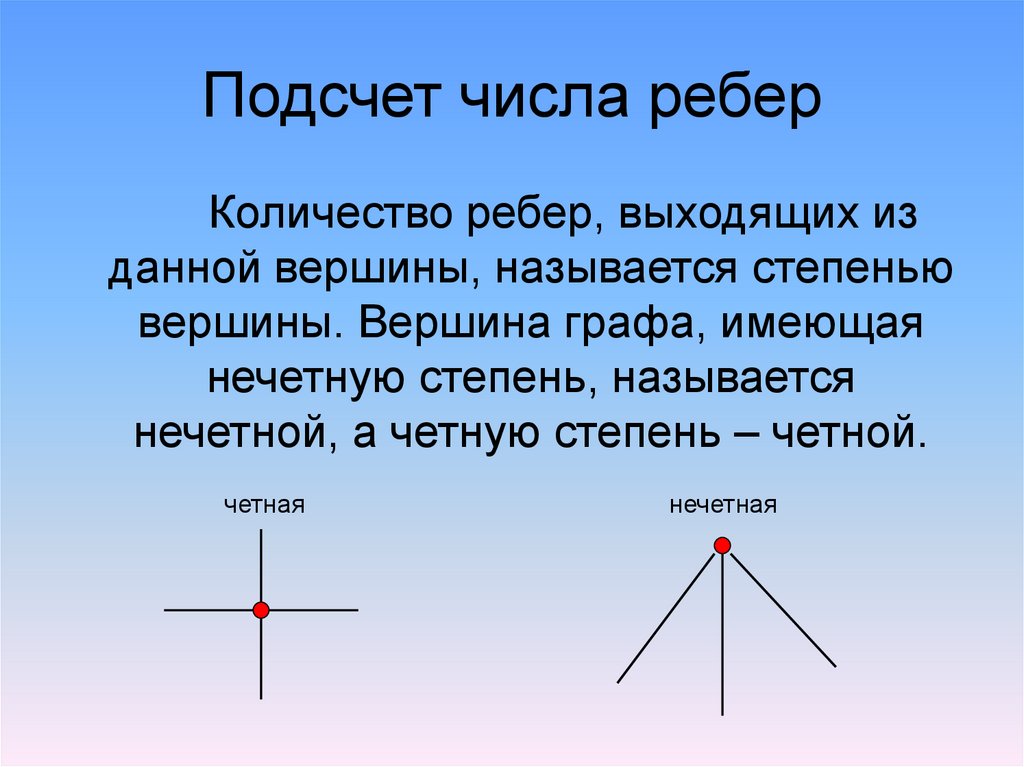
9. Подсчет числа ребер

Количество ребер, выходящих из
данной вершины, называется степенью
вершины. Вершина графа, имеющая
нечетную степень, называется
нечетной, а четную степень – четной.
четная
нечетная

10. Задача

В городе Маленьком 15 телефонов.
Можно ли их соединить проводами так,
чтобы каждый телефон был соединен
ровно с пятью другими?
Решение.
Пусть это возможно. Рассмотрим граф, вершины которого
соответствуют телефонам, а ребра – соединяющим их
проводам. В этом графе 15 вершин, степень каждой из которых
равна 5.Для подсчета количества ребер в этом графе сложим
степени всех его вершин. При таком подсчете каждое ребро
учтено дважды. Поэтому число ребер графа должно быть равно
15 · 5 / 2. Но это число нецелое. Значит,такого графа не
существует и соединить телефоны невозможно.

11. Задача

В государстве 50 городов, и из каждого выходит 8
дорог. Сколько всего дорог в государстве?
Решение.
50 · 8 / 2 = 200 дорог
Теорема. Число нечетных вершин любого графа
четно.
Доказательство. Количество ребер графа равно
половине суммы степеней его вершин. Так как
количество ребер должно быть целым числом, то
сумма степеней вершин должна быть четной. А это
возможно только в том случае, если граф содержит
четное число нечетных вершин.

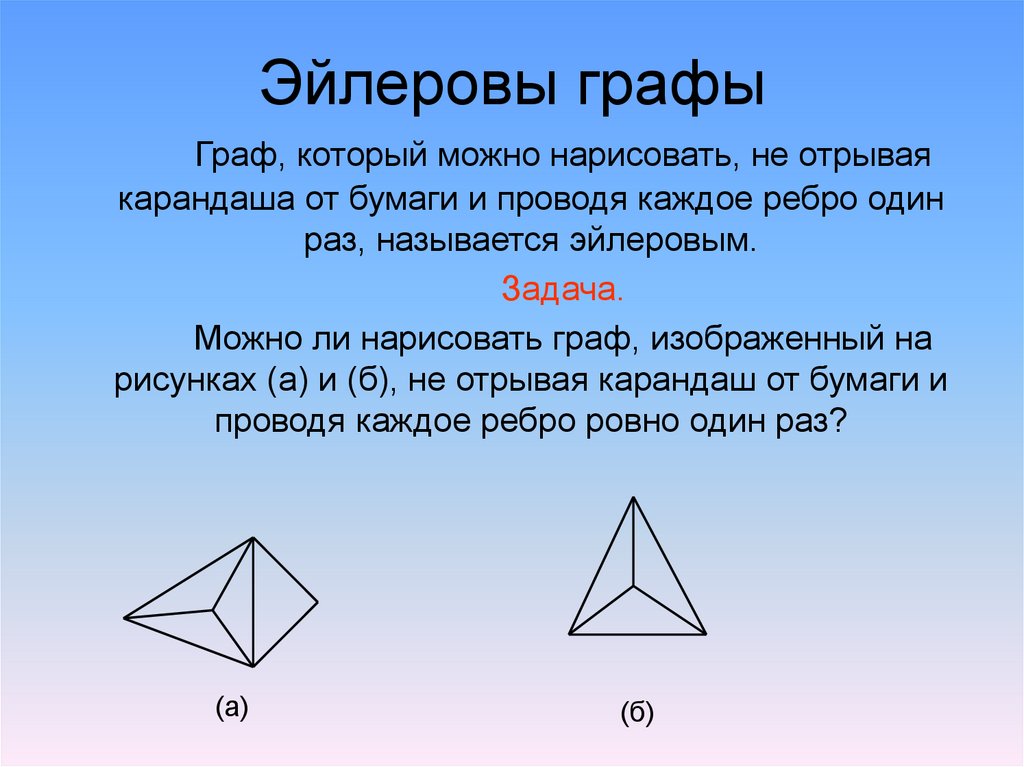
12. Эйлеровы графы

Граф, который можно нарисовать, не отрывая
карандаша от бумаги и проводя каждое ребро один
раз, называется эйлеровым.
Задача.
Можно ли нарисовать граф, изображенный на
рисунках (а) и (б), не отрывая карандаш от бумаги и
проводя каждое ребро ровно один раз?
(а)
(б)

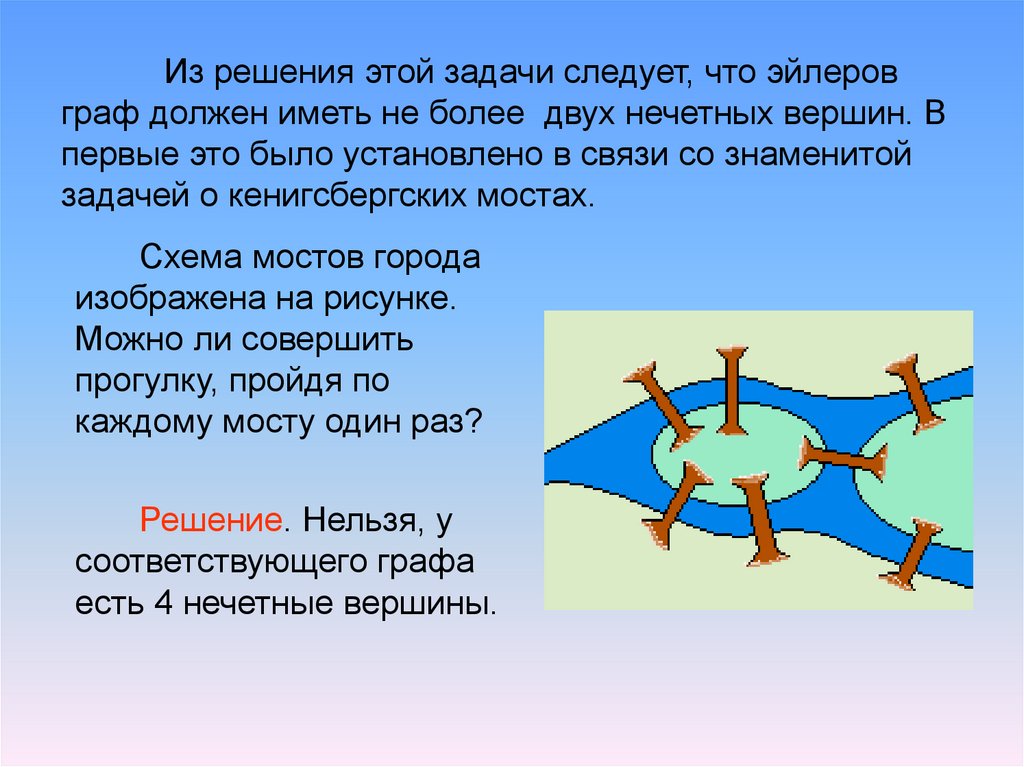
13. Из решения этой задачи следует, что эйлеров граф должен иметь не более двух нечетных вершин. В первые это было установлено в

связи со знаменитой
задачей о кенигсбергских мостах.
Схема мостов города
изображена на рисунке.
Можно ли совершить
прогулку, пройдя по
каждому мосту один раз?
Решение. Нельзя, у
соответствующего графа
есть 4 нечетные вершины.

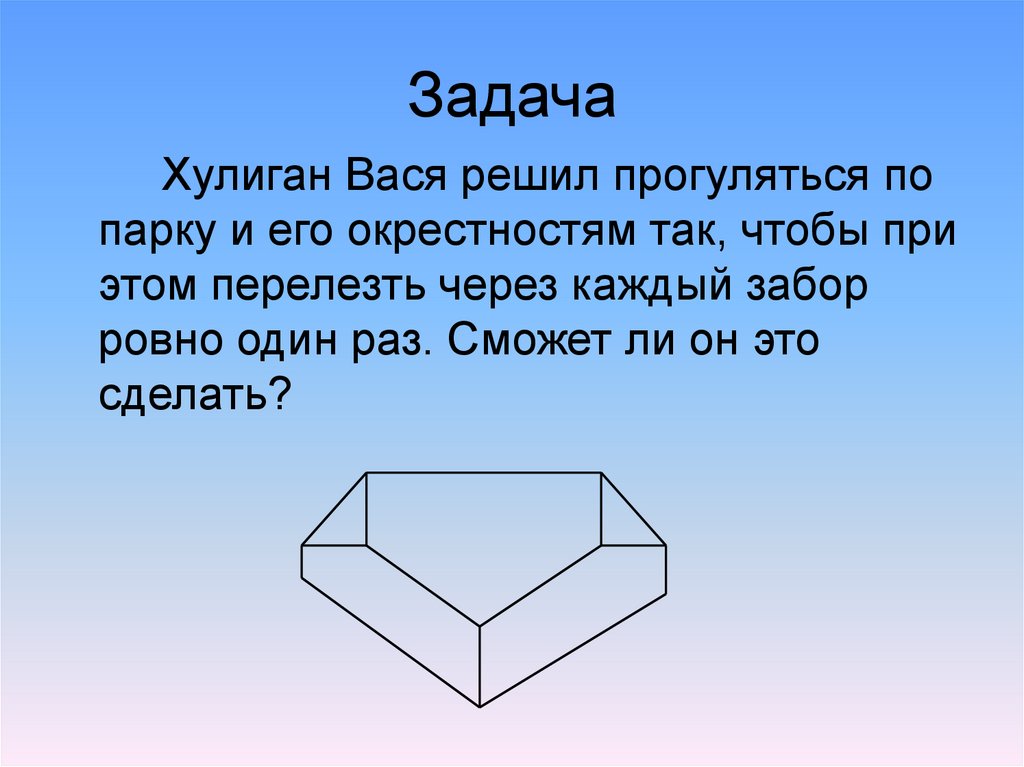
14. Задача

Хулиган Вася решил прогуляться по
парку и его окрестностям так, чтобы при
этом перелезть через каждый забор
ровно один раз. Сможет ли он это
сделать?

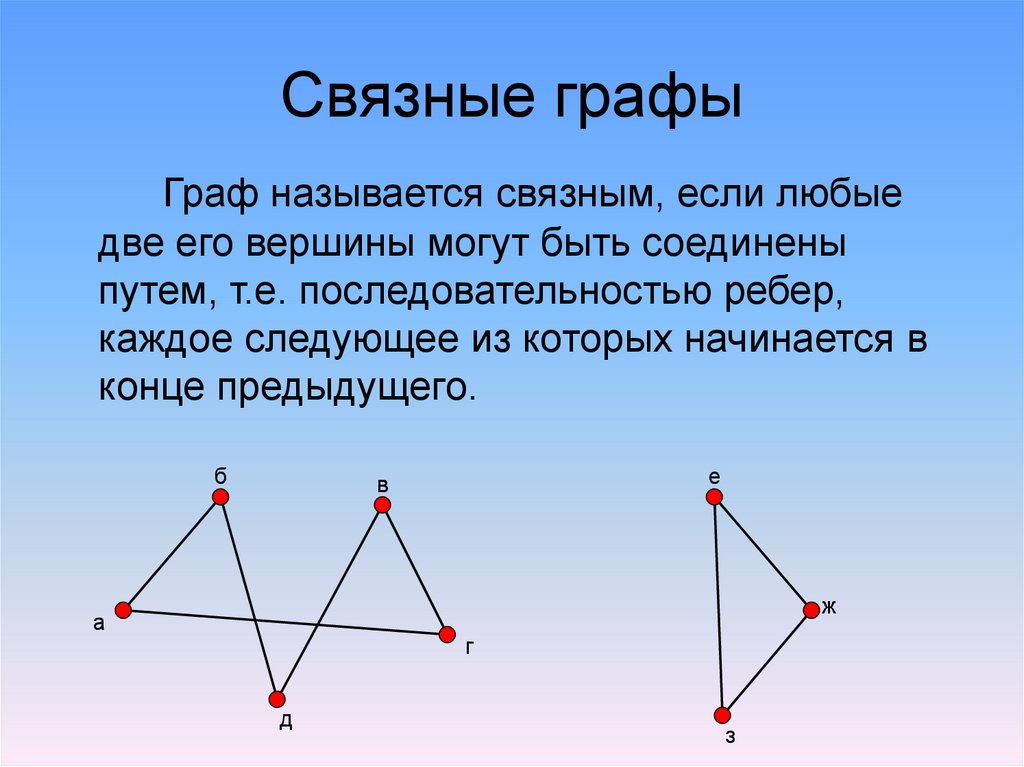
15. Связные графы

Граф называется связным, если любые
две его вершины могут быть соединены
путем, т.е. последовательностью ребер,
каждое следующее из которых начинается в
конце предыдущего.
б
е
в
ж
а
г
д
з

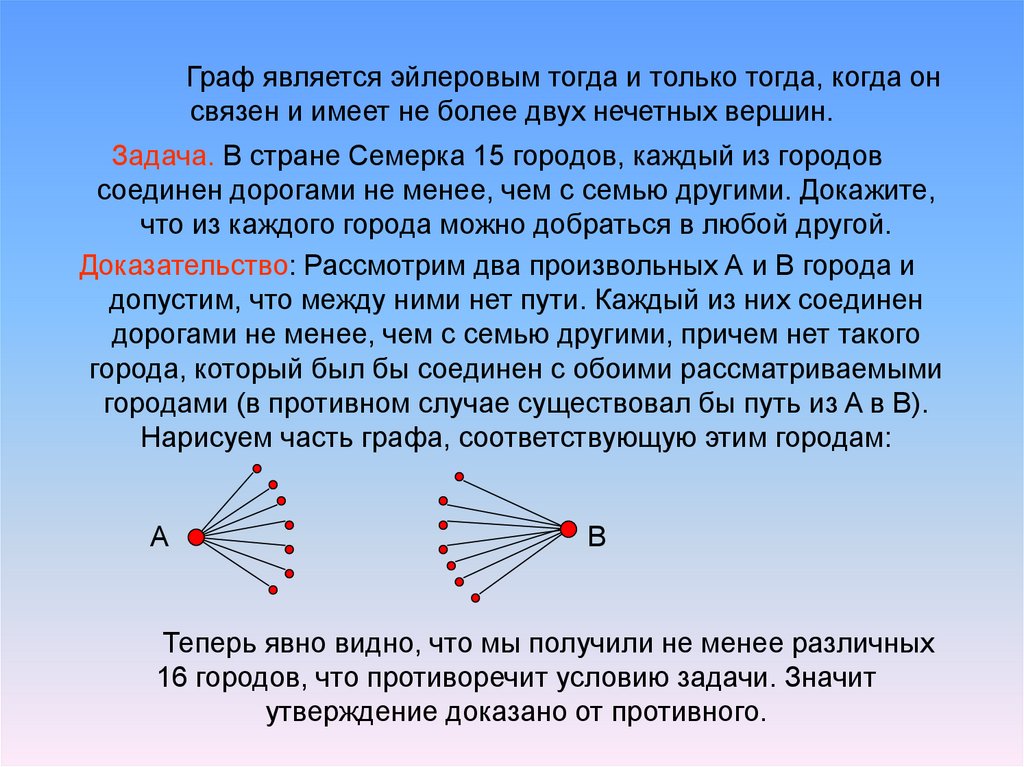
16. Граф является эйлеровым тогда и только тогда, когда он связен и имеет не более двух нечетных вершин.

Задача. В стране Семерка 15 городов, каждый из городов
соединен дорогами не менее, чем с семью другими. Докажите,
что из каждого города можно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и
допустим, что между ними нет пути. Каждый из них соединен
дорогами не менее, чем с семью другими, причем нет такого
города, который был бы соединен с обоими рассматриваемыми
городами (в противном случае существовал бы путь из A в B).
Нарисуем часть графа, соответствующую этим городам:
А
В
Теперь явно видно, что мы получили не менее различных
16 городов, что противоречит условию задачи. Значит
утверждение доказано от противного.

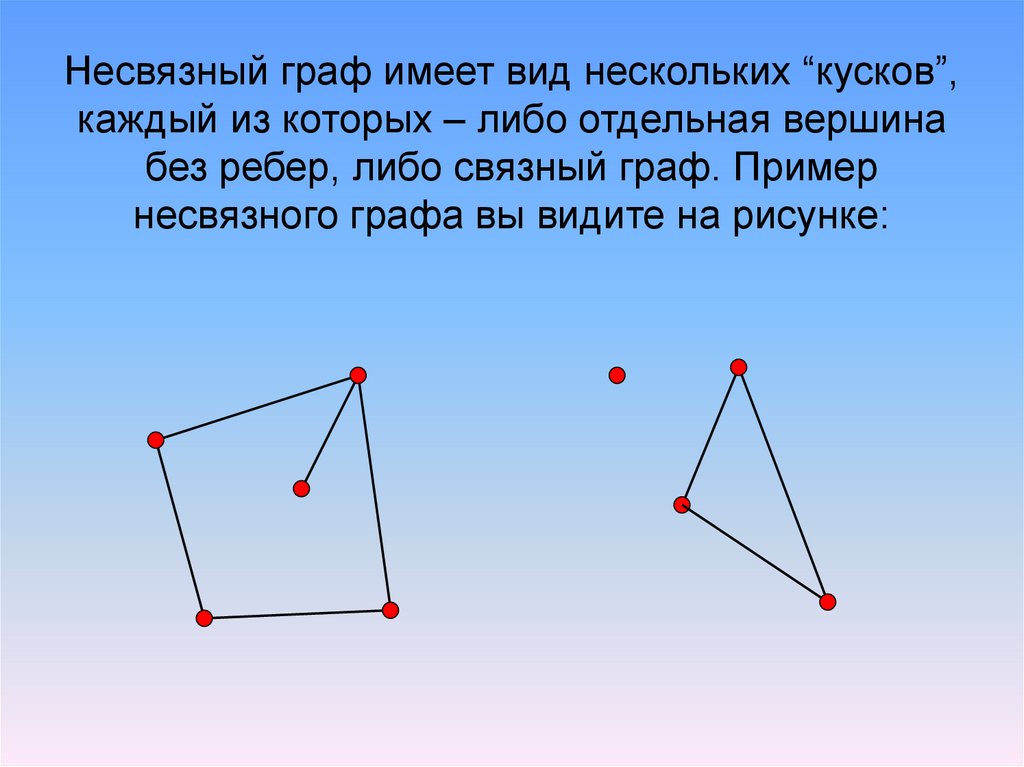
17. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример

несвязного графа вы видите на рисунке:

18. Деревья

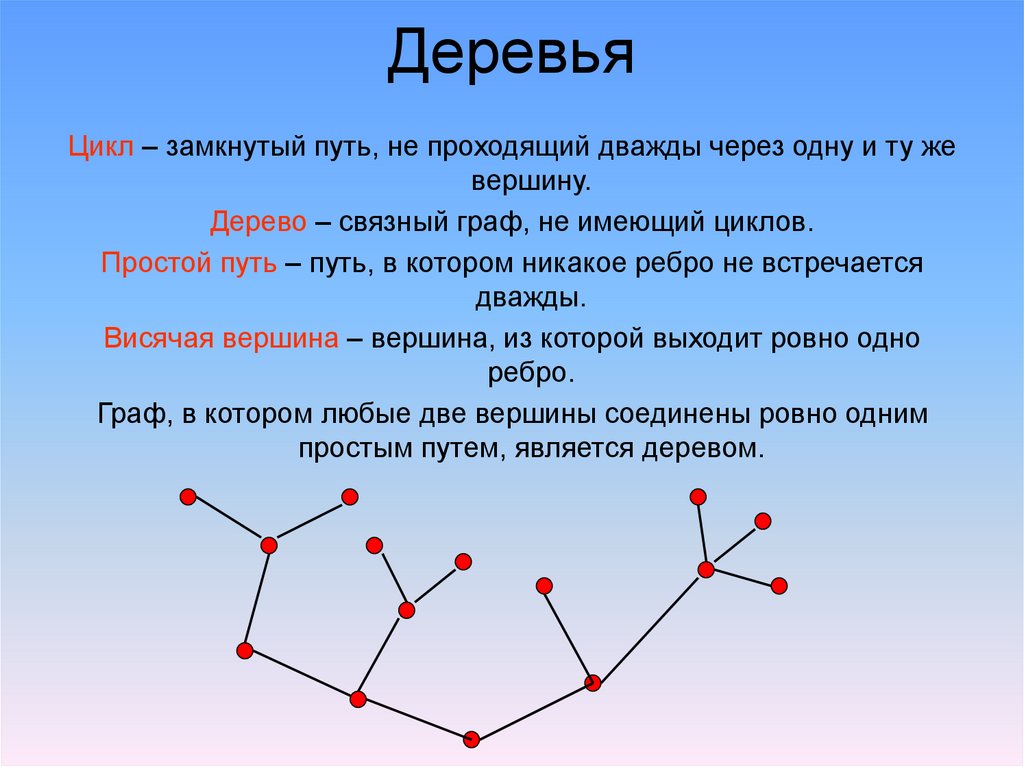
Цикл – замкнутый путь, не проходящий дважды через одну и ту же
вершину.
Дерево – связный граф, не имеющий циклов.
Простой путь – путь, в котором никакое ребро не встречается
дважды.
Висячая вершина – вершина, из которой выходит ровно одно
ребро.
Граф, в котором любые две вершины соединены ровно одним
простым путем, является деревом.

19. Плоские графы

Плоским графом называется граф,
который можно нарисовать так, что бы
его ребра не пересекались нигде, кроме
вершин.

20.

В трех различных домах живут три поссорившиеся между собой соседа.
Недалеко от их домов имеются три колодца. Можно ли от каждого дома
проложить к каждому из колодцев тропинку так, чтобы никакие две из них
не пересекались?
Решение
Проведенные в графе на рисунке ребра А1, А2, A3 и В1,В2, ВЗ
(соответствующие тропинкам от домов А и В ко всем колодцам). Построенный
граф разбил плоскость на три области: X, У, Z. Вершина Б, в зависимости от ее
расположения на плоскости, попадает в одну из этих трех областей. Если
рассмотреть каждый из трех случаев «попадания» вершины Б в одну из
областей X, Y или Z, то всякий раз одна из вершин графа 1, 2 или 3 (один из
колодцев) будет «недоступной» для вершины Б (т. е. нельзя будет провести
одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе
ребер).
Таким образом, ответ на вопрос задачи будет таким: «Нельзя!»

21. Формула Эйлера

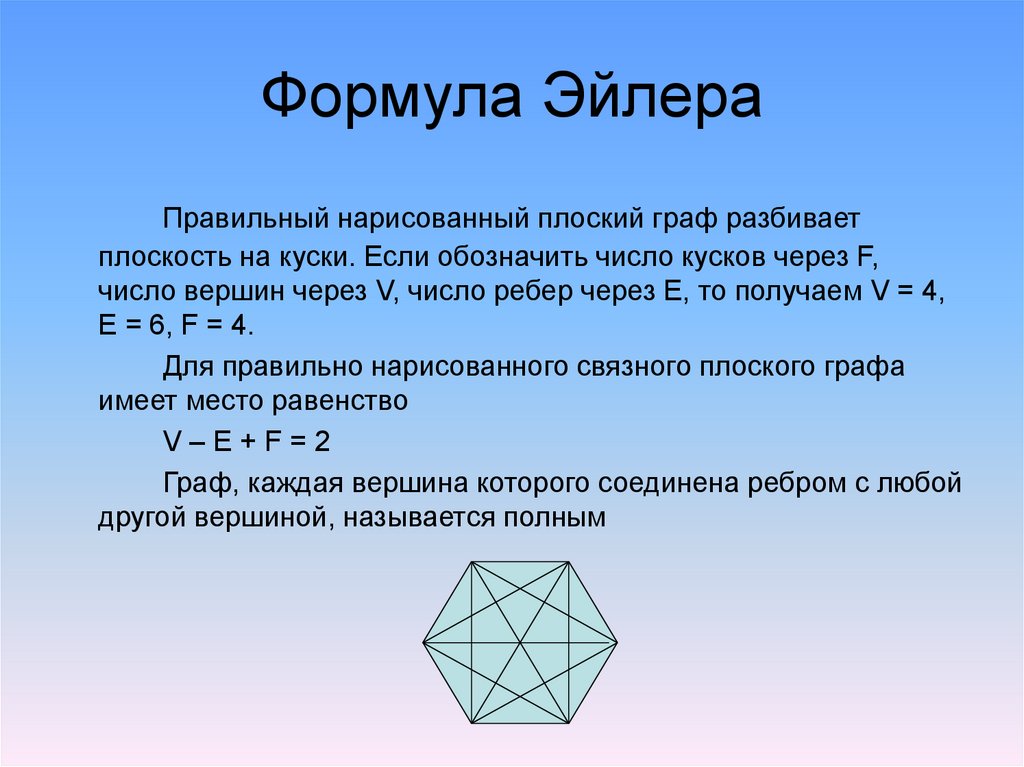
Правильный нарисованный плоский граф разбивает
плоскость на куски. Если обозначить число кусков через F,
число вершин через V, число ребер через E, то получаем V = 4,
Е = 6, F = 4.
Для правильно нарисованного связного плоского графа
имеет место равенство
V–E+F=2
Граф, каждая вершина которого соединена ребром с любой
другой вершиной, называется полным

22. Ориентированные графы

Граф, на ребрах которого расставлены стрелки,
называется ориентированным.
Задача. Дима, приехав из Врунляндии, рассказал, что
там есть несколько озер, соединенных между собой
реками. Из каждого озера вытекает три реки и в
каждое озеро впадает четыре реки. Докажите, что он
ошибается.
Решение.
Количество «втекающих» рек должно быть ровно
общему количеству «вытекающих» рек.

23. Задача

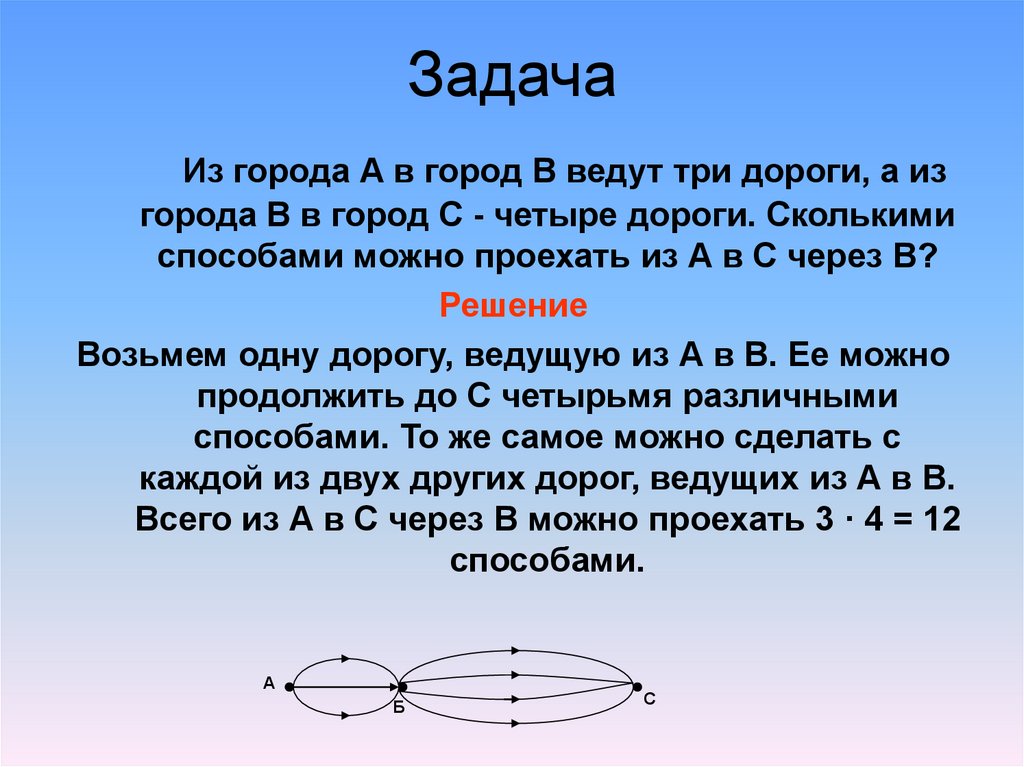
Из города А в город В ведут три дороги, а из
города В в город С - четыре дороги. Сколькими
способами можно проехать из А в С через В?
Решение
Возьмем одну дорогу, ведущую из А в В. Ее можно
продолжить до С четырьмя различными
способами. То же самое можно сделать с
каждой из двух других дорог, ведущих из А в В.
Всего из А в С через В можно проехать 3 · 4 = 12
способами.
А
Б
С

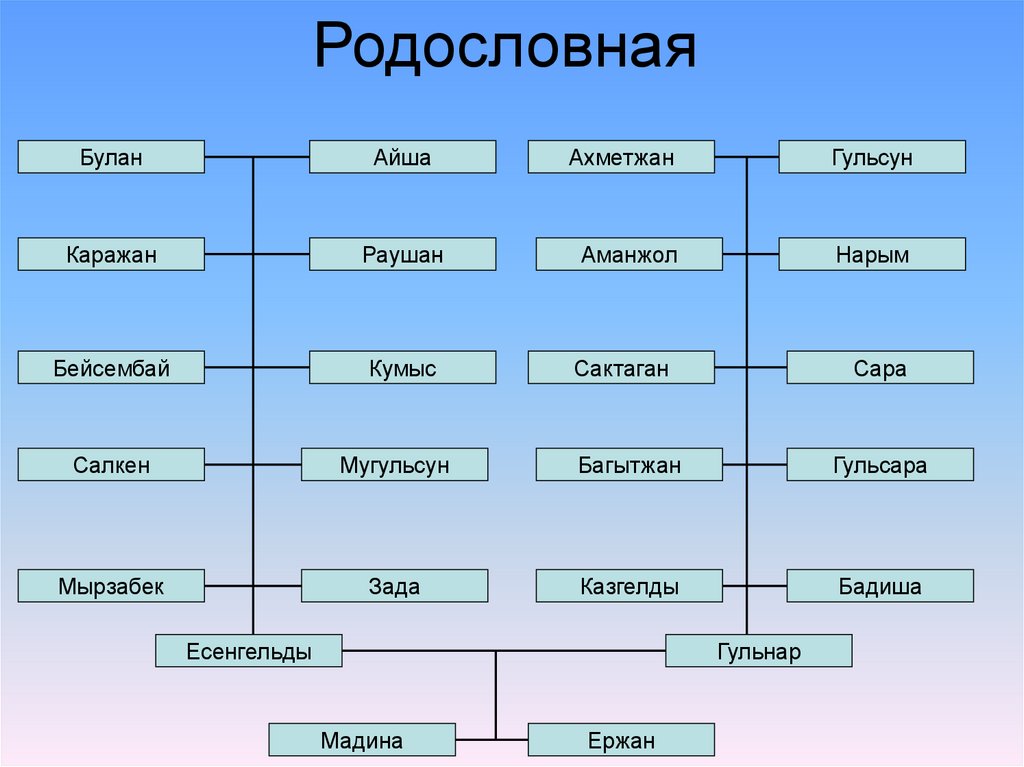
24. Родословная

Булан
Айша
Ахметжан
Гульсун
Каражан
Раушан
Аманжол
Нарым
Бейсембай
Кумыс
Сактаган
Сара
Салкен
Мугульсун
Багытжан
Гульсара
Мырзабек
Зада
Казгелды
Бадиша
Есенгельды
Гульнар
Мадина
Ержан