Similar presentations:
Комбинаторные задачи. Урок № 100
1. КОМБИНАТОРНЫЕ задачи
УМК: А.Г. Мерзляк и др.5 класс
2. Определение
Комбинаторикой называют областьматематики, изучающую вопросы о числе
различных вариантов наборов (удовлетворяющих
тем или иным условиям), которые можно
составить из данных элементов.
Т.е. – это наука, которая занимается
решением задач на перебор всех возможных
вариантов
3. Определение
Комбинаторными задачаминазываются такие задачи, решая
которые приходится составлять
различные комбинации из конечного
числа элементов и подсчитывать
количество таких комбинаций.
4. Способы решения комбинаторных задач
• Перебор вариантов• Дерево возможных вариантов
• По правилу умножения (в 9 классе)
Чтобы процесс перебора возможных вариантов был
удобным и наглядным, делают это таблицей или
схемой.
Способы решения (перебор вариантов и дерево
возможных вариантов) применяют тогда, когда
элементов перебора немного.
5. Например
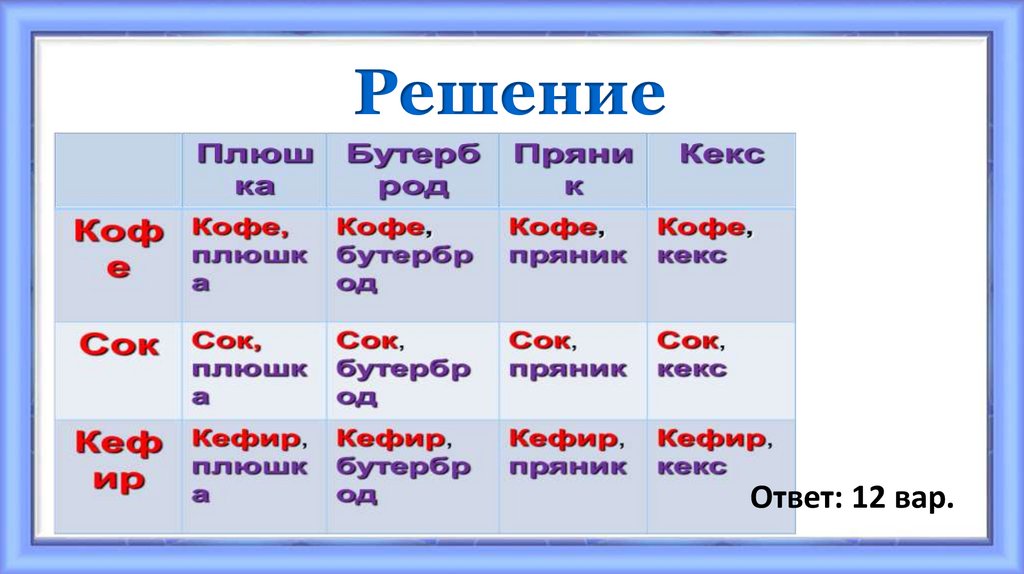
На завтрак Вова может выбратьплюшку, бутерброд, пряник или
кекс, а запить их он может кофе,
соком или кефиром.
Из скольких вариантов завтрака
Вова может выбирать?
6. Решение
Ответ: 12 вар.7. Например
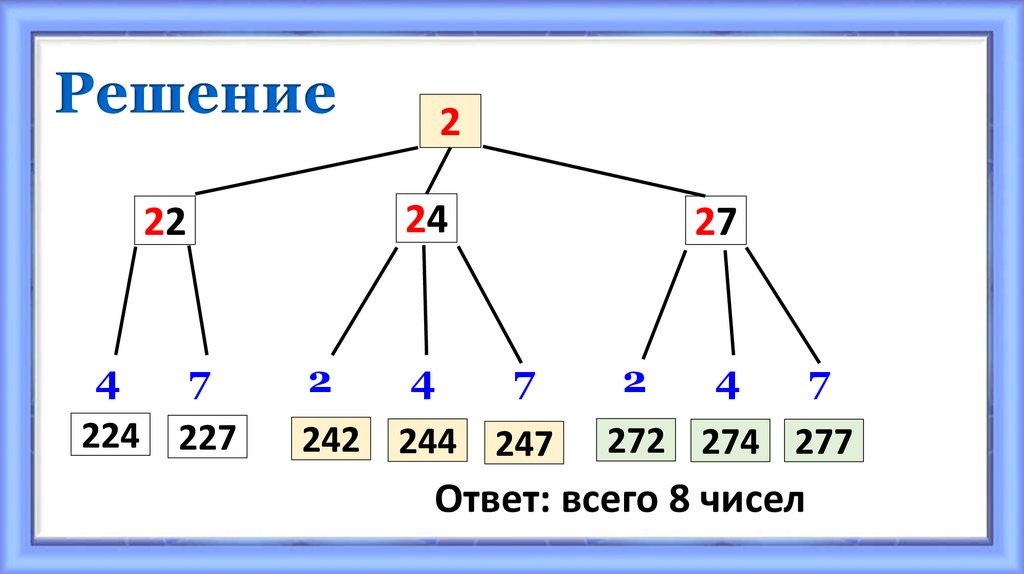
Из цифр 2, 4 и 7 надо составитьтрёхзначное число, в котором ни
одна цифра не может повторятся
более двух раз.
Составим дерево решений (дерево возможных
вариантов) – это схема, графически отражающая
условие задачи и ход рассуждений.
8. Решение
2422
4
7
224 227
2
2
4
27
7
242 244 247
2
4
7
272 274 277
Ответ: всего 8 чисел
9. Задача. Одноклассницы Оля, Валя и Катя дежурят по школе. Сколькими способами классный руководитель может расставить девочек по
одной на каждом из трёхэтажей школы?
Решение.
составим схему – дерево возможных вариантов (см. стр. 161)
Или просто переберём: ОВК;ОКВ; ВОК;ВКО; КОВ;КВО
Ответ: 6 вариантов
10. Задача. При встрече 4 приятеля обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Решение. Назовём приятелей А; В; С и D.Составим схему
А
В
D
С
Ответ: 6 вариантов
11. Задача. Запишите все двузначные числа, в записи которых используются только цифры 1; 2 и 3 (цифры могут повторятся)
Решение.Первая цифра
Вторая цифра
Двузначное число
1
2
1
2
3
Варианты числа: 11; 12; 13;
1
2
(цифры могут повторятся)
3
3
21; 22; 23;
1
2
3
31; 32; 33
Ответ: 9 чисел
12. Задача. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0; 1 и 2?
Решение.Двузначное число
1
Первая цифра
Вторая цифра
Варианты числа:
0
(цифры не могут повторятся)
2
2
0
1
10; 12; 20; 21
Ответ: 4 числа
13. Задача. Запишите все 3-хзначные числа, в записи которых используются только цифры 3; 4 и 6 (цифры не могут повторятся)
Задача. Запишите все 3-хзначные числа, взаписи которых используются только цифры 3;
4 и 6 (цифры не могут повторятся )
Решение.
трёхзначное число (цифры
Первая цифра
3
4
Вторая цифра
4 6
3 6
Третья цифра
6 4
6
3
Назовите числа:
Ответ: 6 чисел
не могут повторятся)
6
3
4
4
3
14. Задача. У ослика Иа-Иа есть 3 надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям:
Винни-Пуху, Пятачкуи Кролику. Сколько есть вариантов и Иа-Иа?
Решение.
шарики
красный
зелёный
жёлтый
Винни-Пух
красный
зелёный
жёлтый
Пятачок
зелёный
жёлтый
жёлтый
красный
красный
зелёный
Кролик
жёлтый
зелёный
красный
жёлтый
зелёный
красный
друзья
Ответ: 6 вариантов
15. Задача. В футбольном турнире участвовали команды 5 «А», 5 «Б» и 5 «В» классов. Сколько существует способов распределения 1-го и
2-го мест среди этих команд?Решение.
Команды
5 «А»
5 «Б»
5 «В»
1 место
+
2 место
+
2 место
+
Ответ: 6 спос.
Значит: если 5 «А» займёт 1 место, то - 2 варианта
Аналогично, если 5 «Б» займёт 1 место, то - 2 варианта
если 5 «В» займёт 1 место, то ещё - 2 варианта
16. Решить самостоятельно
Задача. Запишите все 3-хзначныечисла, в записи которых используются
только цифры 4; 7 и 0 (цифры не могут
повторятся)
Ответ: ??? чисел
17. Решить самостоятельно
Задача. Сколько различныхтрёхзначных чисел можно составить из
цифр (цифры могут повторяться):
а) 1 и 2
б) 0 и 1
Ответ: ??? чисел
18. Источники
Шаблон создан на основе клипарта рамки• https://img-fotki.yandex.ru/get/4124/39663434.8ee/0_ace13_53b91bc7_XL.png
И возможностей программы Microsoft PowerPoint 2016
Шаблон презентации подготовила учитель русского языка и литературы Тихонова Надежда
Андреевна, г. Костанай
А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Математика: 5 класс:
учебник для учащихся общеобразовательных организаций, - 2-е
изд., перераб. – М.:Вентана-Граф, 2016
https://cdn.eksmo.ru/v2/VEN000000000009285/COVER/cover13d.jpg
















 mathematics
mathematics








