861.97K

Category: $mathematics$ mathematics

Графики, уравнения, неравенства

2.

Как алгебраисты
вместо АА, ААА, …
пишут А2, А3, …
так я вместо
1 1 1
, 2, 3
а а а
пишу а-1, а-2, а-3, …
Ньютон И.

3.

Нам знакомы функции:
у
Парабола
у = х2
у
Прямая
у=х
х
х
у
у Все эти функции являются частными
случаями степенной функции
х
у=
х3
Кубическая
парабола
х
1
у
х
Гипербола

Определение:
Степенной функцией
называется функция вида
где р – заданное
действительное
число
Свойства и график степенной функции
зависят от свойств степени с
действительным показателем, и в частности
от того, при каких значениях х
ир
имеет
смысл степень хр.

5.

Степенная функция:
Показатель р = 2n – четное натуральное
число у = х2, у = х4 , у = х6, у = х8, …
D( y ) : x R
Е ( y) : у 0
у
у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
[0; )
на промежутке
0
1
х

6.

Степенная функция:
Показатель р = 2n – четное натуральное
число у = х2, у = х4 , у = х6, у = х8, …
y
у = х2
у = х4
у = х6
-1 0
1
2
x

7.

Степенная функция:
Показатель р = 2n-1 – нечетное натуральное
число у = х3, у = х5 , у = х7, у = х9, …
D( y ) : x R
Е ( y) : у R
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
Функция возрастает на
промежутке
0 1

8.

Степенная функция:
Показатель р = 2n-1 – нечетное натуральное
число у = х3, у = х5 , у = х7, у = х9, …
y
у = х3
у = х5
у = х7
-1 0
1
2
x

9.

Степенная функция:
Показатель р = -2n – где n натуральное
число у = х-2, у = х-4 , у = х-6, у = х-8, …
D( y ) : x 0
Е ( y) : у 0
Функция у=х-2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
( ;0)
0 1
промежутке
Функция убывает
(0; ) на промежутке
y х
2
1
y 2
х

10.

Степенная функция:
Показатель р = -2n – где n натуральное
число у = х-2, у = х-4 , у = х-6, у = х-8, …
y
у = х-2
у = х-4
у = х-6
-1 0
1
2
x

11.

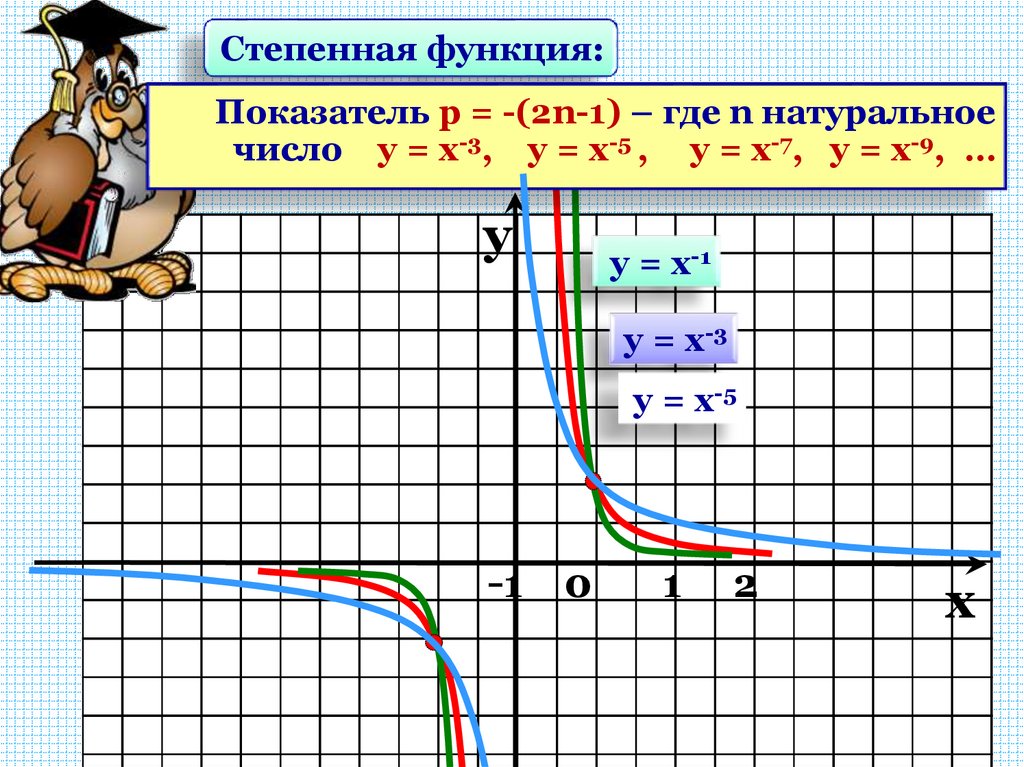
Степенная функция:
Показатель р = -(2n-1) – где n натуральное
число у = х-3, у = х-5 , у = х-7, у = х-9, …
D( y ) : x 0
Е ( y) : у 0
Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на
(
;0)
промежутке
0 1
Функция убывает
(0; )
на промежутке
y х
1
1
y
х

12.

Степенная функция:
Показатель р = -(2n-1) – где n натуральное
число у = х-3, у = х-5 , у = х-7, у = х-9, …
y
у = х-1
у = х-3
у = х-5
-1 0
1
2
x

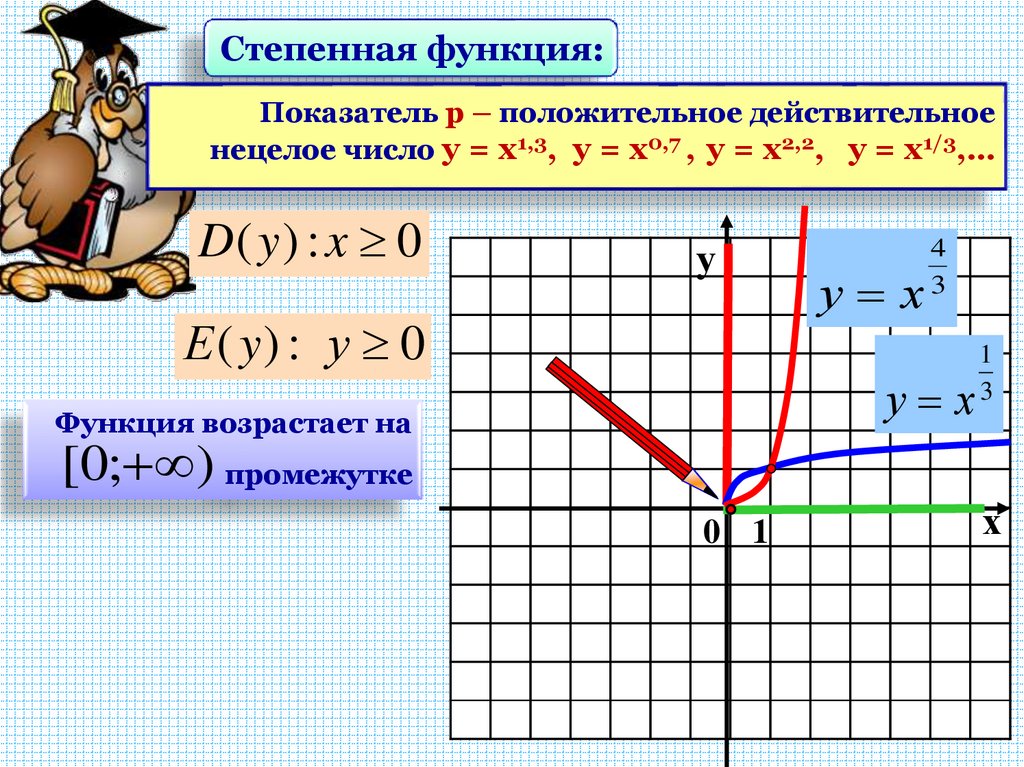
13.

Степенная функция:
Показатель р – положительное действительное
нецелое число у = х1,3, у = х0,7 , у = х2,2, у = х1/3,…
D( y ) : x 0
у
Е ( y) : у 0
у х
4
3
у х
Функция возрастает на
1
3
[0; ) промежутке
0 1
х

14.

Степенная функция:
Показатель р – положительное действительное
нецелое число у = х1,3, у = х0,7 , у = х2,2, у = х1/3,…
y
у = х0,84
у = х0,7
у = х0,5
-1 0
1
2
x

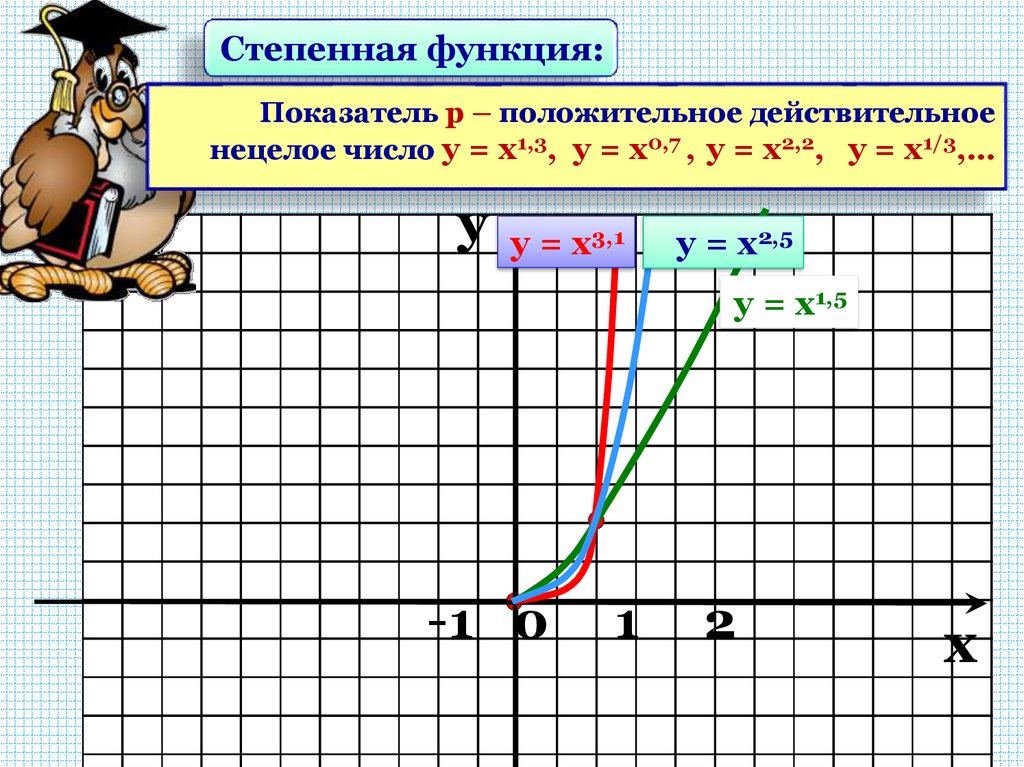
15.

Степенная функция:
Показатель р – положительное действительное
нецелое число у = х1,3, у = х0,7 , у = х2,2, у = х1/3,…
y
у = х3,1
у = х2,5
у = х1,5
-1 0
1
2
x

16.

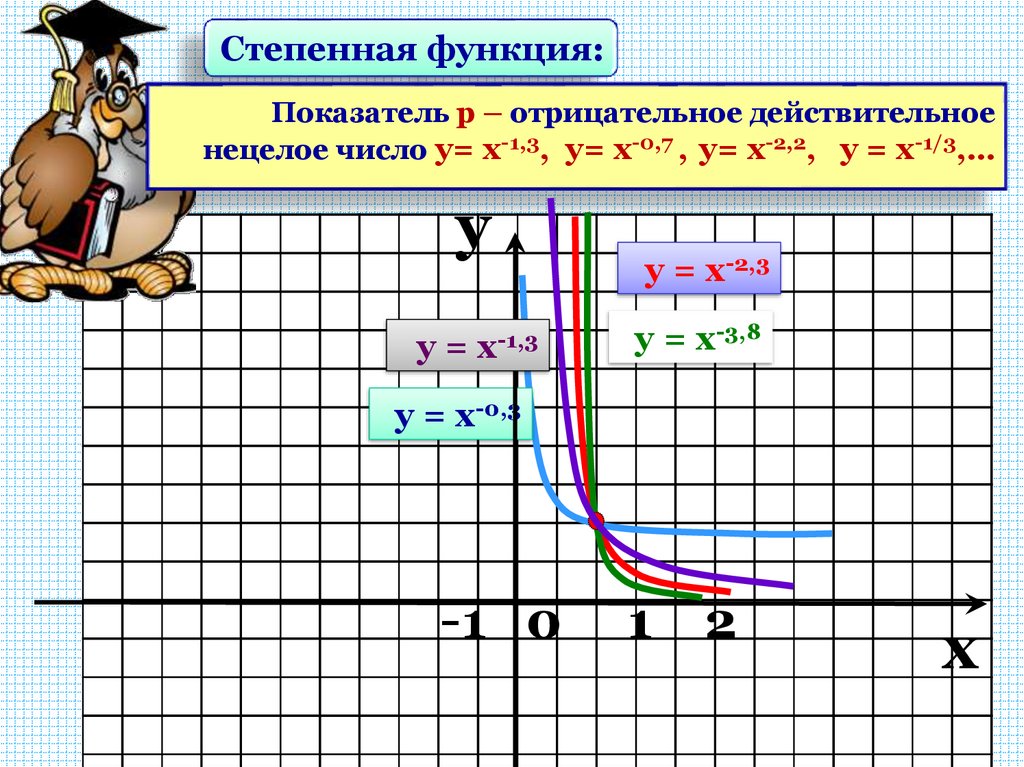
Степенная функция:
Показатель р – отрицательное действительное
нецелое число у= х-1,3, у= х-0,7 , у= х-2,2, у = х-1/3,…
D( y ) : x 0
Е ( y) : у 0
у
Функция убывает на
(0; )
промежутке
0 1
х

17.

Степенная функция:
Показатель р – отрицательное действительное
нецелое число у= х-1,3, у= х-0,7 , у= х-2,2, у = х-1/3,…
y
у=
х-1,3
у = х-2,3
у = х-3,8
у = х-0,3
-1 0
1
2
x

18.

Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий

19.

Понятие логарифмической функции
Функцию вида
y = logaх, где а ≠ 1, a > 0, х > 0
называют
логарифмической функцией

20.

Построим график функции
y=log2x
y=log0.5x
x
1/4 1/2
1 2
4
8
y
-2
y
0 1
2
3
-1
x
1/4 1/2 1
2
4
8
y
2
-1
-2
-3
1
0
y=log2x
3
2
1
4
8
1
x
-2
-3
4
8
x
y=log0.5x

21.

Свойства функции
y
y
x
x
y=logax
a>1
Свойства функции y=loga x, при a>1
1) D(F):(0;+∞)
2) не является ни четной, ни нечетной
3) возрастает на своей области
определения
4) не ограничена ни сверху, ни снизу
5) не имеет ни наибольшего, ни
наименьшего значений
6) непрерывна
7) E(F):(- ∞;+ ∞)
8) выпукла вверх
y=logax 0<a<1
Свойства функции y=loga x, при 0<a<1
1) D(F):(0;+∞)
2) не является ни четной, ни нечетной
3) убывает на своей области определения
4) не ограничена ни сверху, ни снизу
5) не имеет ни наибольшего, ни
наименьшего значений
6) непрерывна
Устно
7) E(F):(- ∞;+ ∞)
Выполняем задание
8) выпукла вниз

22.

y
График
логарифмической
функции
называют
логарифмической
кривой.
y log 2 x
3
2
1
-1
-2
-3
0
1 2
4
y log 1 x
x
8
2
22

23.

1) y = log3 x;
2) y = log2 x;
3) y = log0,2 x;
4) y = log0,5 (2x+5);
5) y = log3 (x+2)
23

24.

Логарифмическая комедия
математический софизм
«2>3»
1 1
очевидно
4 8
2
1 1
2 2
2
3
1
1
lg lg
2
2
3
1
1
2 lg 3 lg
2
2
2 3 неверно!!!

25.

Показательная
функция
y=а
x;
где а>0, a ≠ 1
Выполнила учитель
математики МОУ

26.

График показательной функции
5
4
3
2
1
-5
-4
-3
-2
-1 -10
-2
-3
-4
-5
х
У=(1/2)
0<a<1
У=ах
a>1х
У=2
Y
х
у
-2 -1 0
1
5
4
3
2
1
2
X
1
2
3
4
5
-5
-4
-3
-2
-1 -10
-2
-3
-4
-5
Y
X
1
2
3
4
5

27.

Свойства показательной функции
свойства
a>1
0<a<1
ООФ
Хє(-∞;+∞)
ОЗФ
Ує(0;+∞)
монотонность
Наибол. и
наимен. знач.
Нули
непрерывность
возрастает
убывает
Не существует
Не существуют
Непрерывна на всей ООФ

28.

Логарифмические неравенства

29.

Неравенство, содержащее переменную
только под знаком логарифма, называется
логарифмическим.
Например, неравенства вида:
log a f x log a x log a f x log a x
При а>0,а 1 являются
логарифмическими

30.

По определению логарифма
Простейшие логарифмические неравенства записывается
следующим образом: log a f ( x) b log a f ( x) b
Схема сравнения логарифмических неравенств.
logа x > b
0<a<1
0 < x < ab
logа x < b
a>1
0<a<1
a>1
x > ab
x > ab
0 < x < ab

31.

• Устная работа
• Решить неравенство:
• а)Log 2 Х > Log 2 8;
• б)Log 0,2 4Х < Log 0,2 10;
• в)Log 0,5 Х > Log 0,5 2;
• г)Log 4 2x < Log 4 20.

32.

Логарифмические неравенства. Примеры
Пример 1
log3 2x 4 log3 14 x
log 1 16 4x x 2 4
2
т.к. 3 1, то ф ция возр.
log 1 16 4x x 2
2x 4 14 x ,
2x 4 0,
14 x 0;
2
1
log 1
2 2
4
log 1 16 4x x 2 log 1 16
2
2
1
1, то ф ция убыв.
2
16 4x x 2 16,
16 4x x 2 0; лишнее условие
4x x 2 0
x 2 4х 0
x x 4 0
т.к.
3x 18,
x 2,
x 14;
x 6,
x 2,
x 14;
2
Пример 2
6
Ответ: (6; 14).
14
х
+
0
−
Ответ: [0; 4].
4
+
х