Случайные величины. Тема 3. Часть

1.

ТЕМА 3 ЧАСТЬ 1
СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
Определение случайной величины, случайного вектора. Дискретная
случайная величина (случайный вектор). Распределение вероятностей
случайной величины (случайного вектора). Ряд распределения
дискретной случайной величины, таблица распределения двумерного
дискретного случайного вектора. Функция распределения случайной
величины (случайного вектора) и её свойства.

2.

ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
2

3.

ПРИМЕРЫ СЛУЧАЙНЫХ ВЕЛИЧИН
1.Число родившихся мальчиков среди ста новорожденных есть случайная
величина, которая имеет следующие возможные значения: О, 1, 2, ... , 100.
2. Расстояние, которое пролетит снаряд при выстреле из орудия.
(Действительно, расстояние зависит не только от установки прицела, но и
от многих других причин (силы и направления ветра, температуры и т. д.),
которые не могут быть полностью учтены. Возможные значения этой
величины принадлежат некоторому промежутку (а, b)).
3. Количество электроэнергии потребляемой жителями Оренбурга за 1 месяц.
4. Число бракованных изделий в поступивший партии.
5. число произведенных выстрелов до первого попадания
3

4.

ТИПЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Случайные величины будем обозначать с помощью одной из букв
греческого алфавита , , , ,
кси
эта ню
Наблюденные значения CВ обозначаются с помощью строчных букв
латинского алфавита х, y, z.
Если в качестве результата эксперимента (наблюдения) регистрируется
одно число ( (1) ) , то случайная величина называется одномерной или
скалярной.
Если же результатом каждого эксперимента является регистрация
целого набора интересующих характеристик ( (1) , ( 2) ... ( p ) ) , то
соответствующую случайную величину называют многомерной или
векторной.
Одномерную случайную величину называют дискретной или
непрерывной в зависимости от того, в каком пространстве элементарных
событий она определена – в дискретном или в непрерывном.
4

5.

ТИПЫ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Дискретной - случайная величина, которая принимает отдельные,
изолированные возможные значения с определенными вероятностями. Число
возможных значений дискретной случайной величины может быть конечным
или бесконечным, но счетным. (множество называется счетным, если его
элементы можно перенумеровать натуральными числами.)
2. Непрерывной – случайная величина, которая может принимать
бесконечное несчетное множество значений из некоторого конечного или
бесконечного промежутка.
В нашем примере 1,4 –дискретные случайные величины с конечным
множеством значений
5- дискретные случайные величины с бесконечным, но счетным
множеством значений
2,3 – непрерывные случайные величины.
5

6.

ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ И ИХ ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ
6

7.

СПОСОБЫ ЗАДАНИЯ ДИСКРЕТНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН
Наиболее полным описанием случайной величины является закон ее
распределения.
Определение: Законом распределения случайной величины называется всякое
соотношение, устанавливающее связь между возможными значениями
случайной величины и соответствующими им вероятностями.
7

8.

СПОСОБЫ ЗАДАНИЯ ДИСКРЕТНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН
1. Табличный способ. В таблице перечислены
в порядке
возрастания все возможные значения случайной величины
и
соответствующие их вероятности, т.е
:
хi
х1
х2
…..
хn
pi
p ( х1 ) p1
p ( х2 ) p2
….
p ( хn ) pn
Такая таблица называется рядом распределения дискретной СВ.
Здесь X x1 , х2 ...хn , x1 x2 ...xn - множество возможных значений (n может быть
равно )
События =х1 =х2 … =хn, состоящие в том, что в результате испытания
случайная величина примет соответственно значения х1,х2,…хn образуют
полную группу. Следовательно, сумма их вероятностей равна 1.
n
n
P( x ) p
i 1
i
i 1
i
1
8

9.

СПОСОБЫ ЗАДАНИЯ ДИСКРЕТНЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН
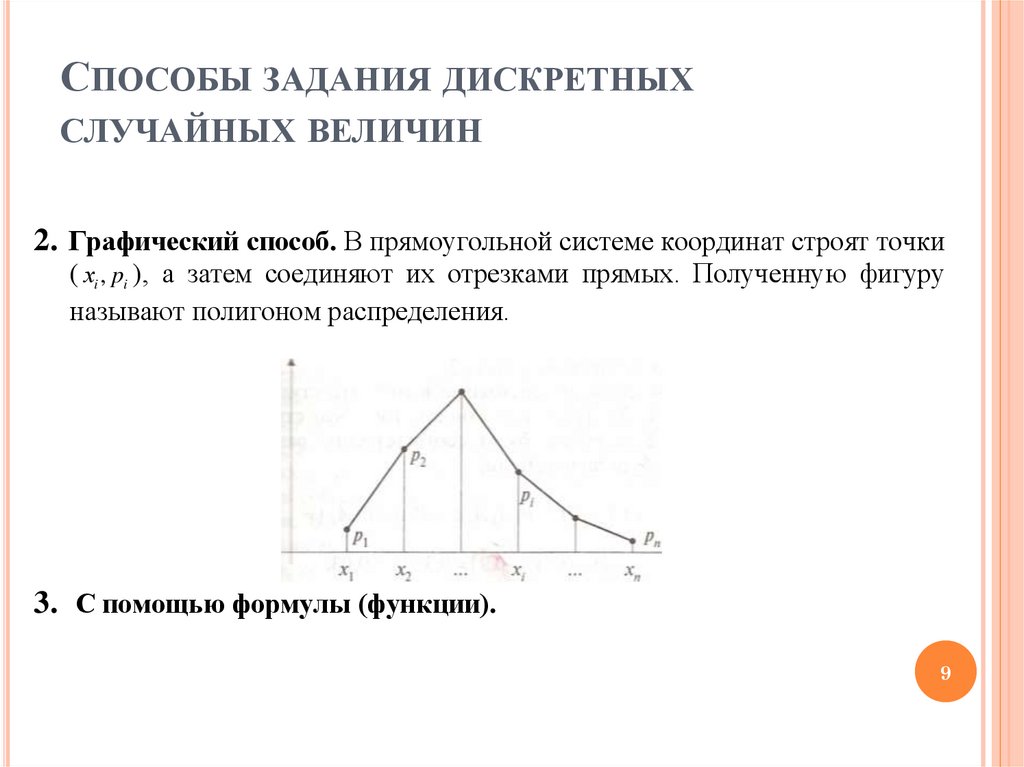
2. Графический способ. В прямоугольной системе координат строят точки
( хi , pi ), а затем соединяют их отрезками прямых. Полученную фигуру
называют полигоном распределения.
3. С помощью формулы (функции).
9

10.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
Функцией распределения вероятностей F ( х ) случайной величины
называют функцию, определяющую вероятность того, что случайная
величина в результате испытания примет значение, меньшее х , т.е.
F ( х )=Р( < х )
В частности, при х xi X ,
F ( х )= p ( x1 ) p ( x2 ) ... p ( xi 1 ) , i 2,...n , F ( х1 )=0
при х xi 1 X
10

11.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ: СВОЙСТВА
1.Значения функции распределения принадлежат отрезку [О, 1]:
F ( x) [0;1]
Доказательство:
Свойство вытекает из определения функции распределения как
вероятности: вероятность всегда есть неотрицательное число, не
превышающее единицы.
2. F (x) -неубывающая функции аргумента х, т.е. F ( x2 ) F ( x1 ) , если x2 x1
11

12.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ: СВОЙСТВА
3. На минус бесконечности функция распределения равна нулю, на плюс
бесконечности равна единице:
F ( ) lim
F ( ) lim
F( x ) 0
F( x ) 1
x
x
Доказательство:
F ( ) Р( ) 0 как вероятность невозможного события
F ( ) Р( ) 1 как вероятность достоверного события
4. Вероятность попадания СВ в интервал ( x1, x2 ) равна приращению функции
распределения на этом интервале:
P( x1 x2 ) P( x2 ) P( x1 ) F ( x2 ) F ( x1 )
Следует из доказательства свойства 2.
12

13.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ: СВОЙСТВА
5. Вероятность того, что непрерывная СВ примет одно определенное
значение, равна нулю. P( x1 ) 0
Доказательство:
Согласно свойству 4. P( x1 x2 ) F ( x2 ) F ( x1 )
P( x1 x1 х) F ( x1 х) F ( x1 )
Устремим х к нулю. Так как Х – непрерывная СВ, то функция F(x)
непрерывна. В силу непрерывности F(x) в точке х1 разность F ( x1 х) F ( x1 )
также стремится к нулю. Следовательно Р( = х1 )=0.
13

14.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
Построим
распределения:
функцию
xi
p xi
x x1
x1 x x 2
x2 x x3
x1
p1
распределения
СВ,
xn
pn
x2
p2
заданной
рядом
F x P : x P 0
def
def
F x P : x P : x 1 p1
def
F x P : x P : x 1 : x 2
P : x 1 P : x 2 p1 p 2
и т.д.
14

15.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
Ряд распределения:
xi
p xi
x1
p1
x2
p2
xn
pn
x x1
0,
p ,
x1 x x2
1
p1 p 2 ,
x 2 x x3
F x
p1 p 2 p3 , x3 x x4
...
x xn
1,
15

16.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
x x1
0,
p ,
x1 x x2
1
p p2 ,
x 2 x x3
F x 1
p1 p 2 p3 , x3 x x4
...
x xn
1,
16

17.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
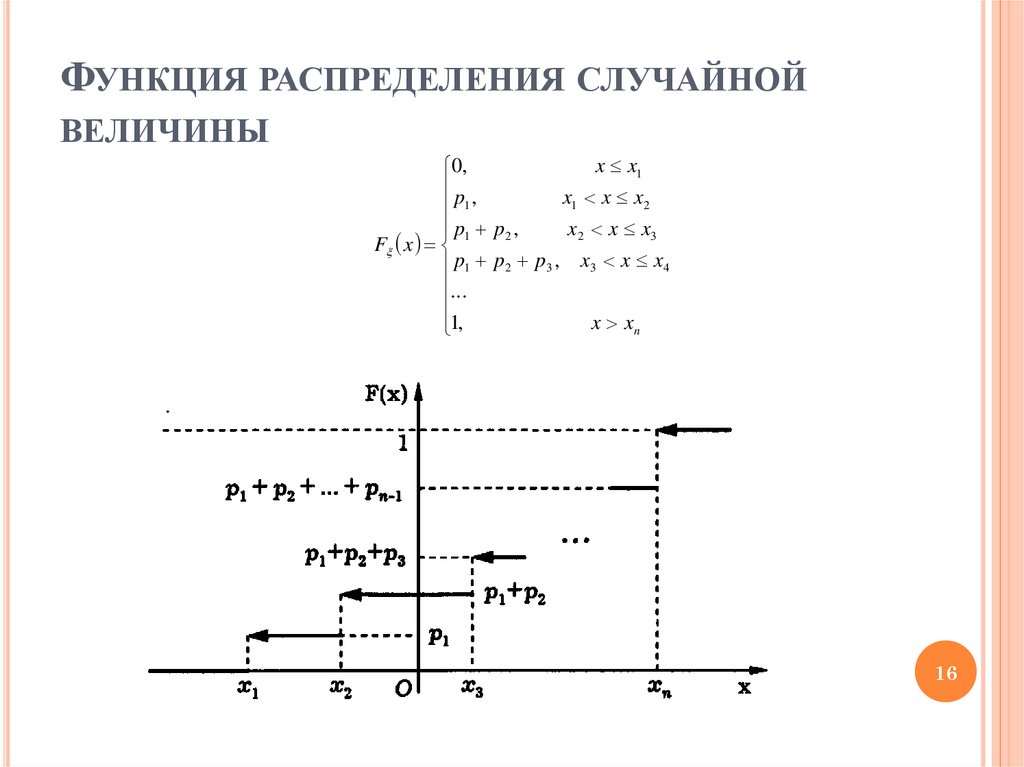
Для дискретной СВ функция распределения является кусочнопостоянной
функцией
(ступенчатой),
которая
в
точках,
соответствующих возможным значениям имеет скачок, равный
вероятности этого возможного значения.
По построению эта функция непрерывна в обычном смысле
везде, за исключением точек, соответствующих возможным
значениям СВ. В них ФР имеет разрыв 1-го рода и имеет предел
слева, следовательно, ФР непрерывна слева.
17

18.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
Дан ряд распределения СВ
:
xi
p (х)
3
0.1
6
0.4
7
0.2
9
0.3
Найти и изобразить ее функцию распределения.
Решение:
F ( х )=Р( < х )
1 Если х 3 , то F( х )=0 (в том числе и при х 3 , F( 3 )=P( <3)=0)
`
`
3
6
7
9
2.Если 3 x 6 (например x 4 )
F( х )=P( =3)=0.1 очевидно, что и F(6)=P( <6)=0.1
3.Пусть 6 x 7
F( х )=Р( < х )=Р( =3)+P( =6)=0.1 +0.4=0.5 очевидно, что и F(7)=P( <7)=0.5
4. Пусть 7 x 9
F( х )=Р( =3)+P( =6)+Р( =7)=0.5 +0,2=0,7 очевидно F(9)=P( <9)=0.7
5. Пусть x 9 F( х )=Р( =3)+P( =6)+Р( =7)+Р( =9)=0.7 +0,3=1
18

19.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ
ВЕЛИЧИНЫ
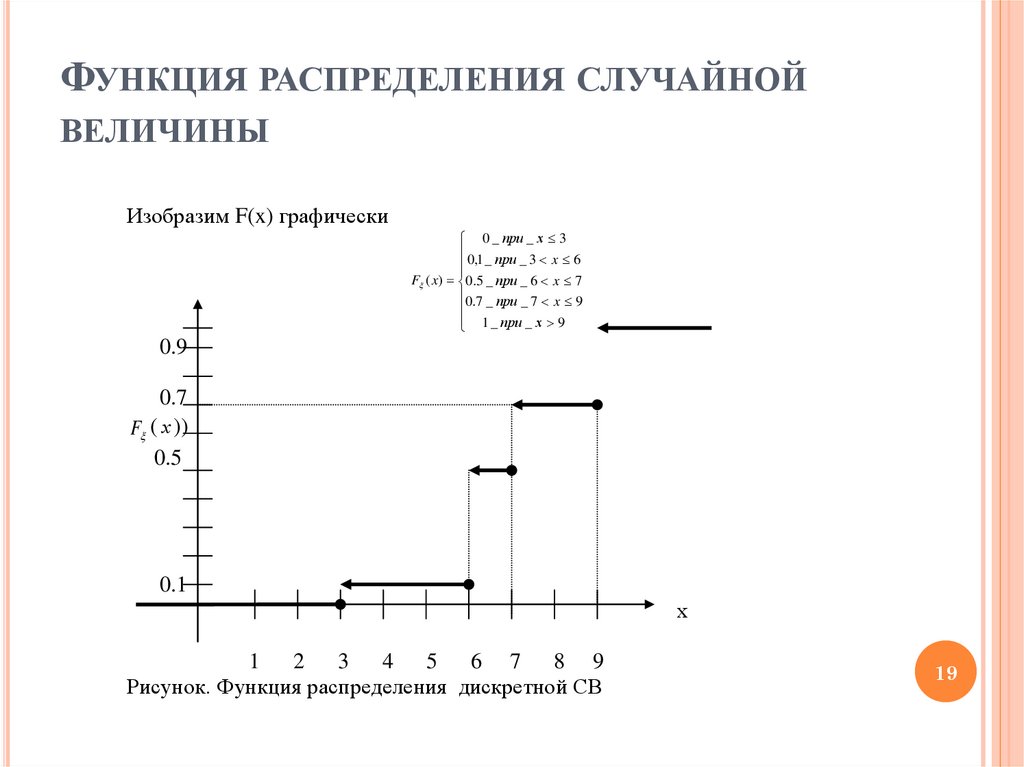
Изобразим F(x) графически
0 _ при _ х 3
0,1 _ при _ 3 x 6
F ( x) 0.5 _ при _ 6 x 7
0.7 _ при _ 7 x 9
1 _ при _ х 9
0.9
0.7
F ( х ))
0.5
0.1
х
4 5 6 7 8 9
1 2 3
Рисунок. Функция распределения дискретной СВ
19

20.

РЯД РАСПРЕДЕЛЕНИЯ ДИСКРЕТНОЙ
ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
В случае двумерной СВ 1 2 T с возможными значениями
1 x (11) , x (21) ,..., x (n1) и 2 x (12) , x (22) ,..., x (m2) закон распределения задается в виде
функции
pij P 1 x (i1) , 2 x (j2) , i 1,2,.., n; j 1,2,.., m
(матрицы) распределения:
1
(1)
x1
(1)
( 2)
x1
p11
2
x (22)
p12
xm
x2
p21
p 22
p 2m
(1)
p 1 ( xi(1) )
( 2)
p1m
xn
pn1
pn 2
p nm
p 2 ( x (j2) )
p*1
p*2
p*m
или в виде таблицы
p1*
p 2*
m
p1 j
j 1
m
p2 j
j 1
p 1 x1(1)
p 1 x2(1)
pn*
pnj p 1 xn(1)
m
j 1
1
20

21.

РЯД РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ ДСВ
По совместному распределению двумерной СВ можно найти
распределение каждой из компонент, которые называются частными
(маргинальными) распределениями СВ и находятся путем суммирования
совместного распределения по всем возможным значениям другой
компоненты. Восстановить же совместное распределение СВ по частным
распределениям в общем случае невозможно.
Для ДСВ 1, , k T закон распределения задается в виде
функции
pij ...k P 1 x (i 1) , 2 x (j2) , , k x (kk ) , i 1,2,.., n1 ; j 1,2,.., n2 ;...; k 1,..., nk .
Тогда pij...k p* j...k - закон распределения СВ 2 , , k T
n1
i 1
n1, n 2,..., nk 1
pij...k
i 1, j 1,..., k 1
p**...*k - закон распределения СВ k .
То есть, просуммировав по возможным значениям k-1 компоненты
получим закон распределения оставшейся одной k-ой компоненты.
21

22.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ
СВ
Функция распределения СВра
F x F 1 , 2 ,..., k x1 , x 2 ,...,x k
- это
функция k действительных переменных, определенная в R k по следующему
правилу x R k :
def
F 1 , 2 ,..., k x 1 , x 2 ,..., x k P : 1 x 1 , 2 x 2 ,..., k x k P : x
22

23.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ
СВ: СВОЙСТВА
Функция распределения задается вероятностью совместного появления k
событий, то есть равна произведению вероятностей появления событий
A i : i x i
1) ФР k –мерного случайного вектора является неубывающей функцией
по каждому аргументу
F x1 , x 2 ,...,x k F x1 ,...,x i 1 , x i x i , x i 1, ,...,x k , x i 0
2) ФР k –мерного случайного вектора является непрерывна слева по
каждому аргументу;
23

24.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ МНОГОМЕРНОЙ
СВ: СВОЙСТВА
3) Удовлетворяет условиям:
F x 1 ,..., x i 1 , , x i 1, ,..., x k lim F x 1 ,..., x k
x i
lim P : 1 x 1 ,..., ,..., k x k P : 0
x i
F x 1 ,..., x i 1 , , x i 1, ,..., x k lim F x 1 ,..., x k
x i
lim P : 1 x 1 ,..., ,..., k x k
x i
P : 1 x 1 ,.. i 1 x i 1 , i 1 x i 1 ,..., k x k
F 1 ,..., i 1 , i 1..., k x 1 ,..., x i 1 , x i 1, ,..., x k
В частности, F , ,..., 1.
Замечание. Таким образом, зная ФР k-мерного СВра, мы можем найти
ФР каждой компоненты или любой их группы. По ФР компоненты или их
24
группы исходную ФР восстановить невозможно.

25.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СВ
В двумерном случае для случайного вектора ( , ) функция распределения
F ( x, y) определяется равенством: F ( x, y) P( x, y) . Функция распределения
векторной случайной величины ( , ) , называется совместной ФР случайных
величин и . По ней легко найти ФР случайных компонент вектора, которые
называются частными функциями распределения.
F (y) = F ( , y)
F (x) = F ( x, )
Частные ФР случайного вектора, соответствующие одной из его компонент,
определяются путем “подстановки ” вместо другой компоненты в выражение
для совместной ФР.
25

26.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СВ
Геометрически функция распределения означает вероятность попадания
случайной точки ( X , Y ) в заштрихованную область (рис.) – бесконечный квадрант,
лежащий левее и ниже точки M ( x, y ) .
y
M ( x, y )
0
Правая и верхняя границы области в квадрант
не включаются – это означает,
что функция распределения непрерывна слева
x
по каждому из аргументов
В случае дискретной двумерной случайной величины ее функция
распределения определяется по формуле:
F ( x, y ) pij ,
i
j
где суммирование вероятностей распространяется на все i , для которых xi x , 26
и все j , для которых y j y .

27.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СВ
1.
Функция распределения F ( x, y)
заключенная между нулем и единицей.
0 ≤ F ( x, y) ≤ 1
есть
неотрицательная
функция,
2.
Функция распределения F ( x, y)
каждому из аргументов:
F ( x2 , y) ≥ F ( x1 , y) , если x2 > x1;
есть неубывающая функция по
F ( x , y2 ) ≥ F ( x , y1 ) , если y2 > y1.
3.
Если хотя бы один из аргументов обращается в , функция
распределения F ( x, y) равна нулю:
F ( , y) = F ( x, ) = F ( , ) = 0;
27

28.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СВ
Если один из аргументов обращается в , функция распределения
становится равной функции распределения случайной величины,
соответствующей другому аргументу:
F ( x, ) = F (x) .
4.
F ( x, y)
F ( , y) = F (y)
F (x) , F (y) – функции распределения случайных величин и , т.е.
F ( x) P( x) , F ( y ) P( y )
5.
На “ ” по всем аргументам функция распределения обращается в
единицу:
где
F ( , ) 1
следует из того, что совместное осуществление достоверных событий ( ) ,
( ) есть событие достоверное.
28

29.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ
ВЕЛИЧИНА (СЛУЧАЙНЫЙ
ВЕКТОР)
29

30.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Если вероятностное пространство является непрерывным, то есть
пространство его элементарных исходов состоит из несчетного множества точек
х R l , и при этом вероятность P задается с помощью неотрицательной
интегрируемой функции р ( х ) , удовлетворяющей свойству:
P A Р А p ( x )dx ,
A
то случайная величина называется абсолютно непрерывной (далее будем говорить
просто непрерывной СВ).
30

31.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Функция р ( х ) называется плотностью распределения вероятностей
случайной величины.
Из определения следует, что функция р ( х ) определена для любого х
принадлежащему промежутку от минус бесконечности до плюс бесконечности, но
вне она равна нулю. Кроме того, по аналогии с дискретной случайной
величиной для плотности всегда выполнено условие нормированности
р ( x )dx p ( x )dx Р P 1
Множество Х (большое), удовлетворяющее условию р ( х ) >0, для любых х
из Х, называется множеством возможных значений случайной величины
(носителем (плотности) распределения).
31

32.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Свойства плотности вероятности
1.Плотности вероятности –неотрицательная функция
p ( х) 0
2. Вероятность попадания непрерывной СВ в интервал [а, b] равна
определенному интегралу от ее плотности вероятности в пределах от а до
b.
b
Р( а b) a p ( x )dx
3. Функция распределения непрерывной СВ может быть выражена через
плотность вероятности по формуле:
x
F ( x ) p ( t )dt
4. Несобственный интеграл в бесконечных пределах от плотности
вероятности непрерывной СВ равен единице:
32
p ( x )dx 1

33.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА:
ПРИМЕР
0 _ при _ x 0
( x 3) 2
_ при _ 0 x 3
Пример: Дана плотность распределения: p ( х )
9
0 _ при _ х 3
Найти функцию распределения F(x).
Решение:
x
F ( x ) p( t )dt
33

34.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА:
ПРИМЕР
x
1. F ( x) 0dt 0
x
2.
3.
(t 3) 2
1 (t 3)3
при 0<x 3 F ( x) 0dx 0
dt 0
9
9
3
2
0
3 ( x 3)
x
х>3 F ( x) 0dx 0
dx 0dx 1
3
9
0
x
( х 3)3
0 =
1
27
0 при x 0
( x 3) 3
F ( х ) 1
при 0 x 3
27
1 при х 3
34

35.

НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА:
ПРИМЕР
Пример. Непрерывная СВ имеет функцию распределения. Нарисовать
ее график, найти плотность распределения и нарисовать ее график.
0 _ при _ х 0
х 2 _ при _ 0 x 1
F( x ) 1 _ при _ х 1
35

36.

НЕПРЕРЫВНЫЙ СЛУЧАЙНЫЙ ВЕКТОР
Пусть n-мерная СВ.
Будем говорить, что он непрерывный, если его Функция распределения
представима в виде
F ( x 1 , х 2 ,..., х n ) p : 1 ( ) x 1 ,..., n ( ) x n )
df
x1 x 2
xn
... р
(u 1 , u 2 ,..., u n )du1du 2 ...du n
Здесь p (x1 ...x n ) - плотность распределения вероятности СВ.
1) p (x1 ...x n ) 0 неотрицательность
2)
... P ( x , x
1
2
,..., x n )dx1dx 2 ...dx n =1 нормированность
36

37.

НЕПРЕРЫВНЫЙ СЛУЧАЙНЫЙ ВЕКТОР
Вектор называется непрерывным, если существует такая неотрицательная
функция p (x1 ...x n ) , называемая плотностью распределения n-мерной СВ,
обладающая свойством нормированности.
Т.к. интеграл с переменным верхним пределом является непрерывной
функцией своего аргумента, отсюда и название СВ – непрерывная.
Функция распределения непрерывной двумерной случайной величины
может быть выражена через ее плотность вероятности
F ( x, y)
р (x, y)
по формуле:
x y
р (t, s) dt ds
37

38.

НЕПРЕРЫВНЫЙ СЛУЧАЙНЫЙ ВЕКТОР
В двумерном случае плотность вероятности (плотность распределения)
непрерывной двумерной случайной величины ( , ) - вторая смешанная частная
производная ее функции распределения, т.е.
2 F ( x , y)
F ( x, y )
р ( x , y)
x y
В многомерном n-мерном случае
n F ... ( x 1 ,..., x n )
р ( x 1 ,..., x n )
x 1 .... x n
1 2
n
38

39.

НЕПРЕРЫВНЫЙ СЛУЧАЙНЫЙ ВЕКТОР
По
плотности распределения векторной СВ ( , ) , называемой
совместной плотностью распределения случайных величин и , можно найти
плотность распределения случайных компонент и , которые называются
частными (маргинальными):
р ( x ) р ( x, y)dy
р ( у) р ( x, y)dx
Частные плотности распределения вероятностей случайного вектора,
соответствующие одной из его компонент, определяются путем
интегрирования совместной плотности распределения по другой компоненте.
39

40.

НЕПРЕРЫВНЫЙ СЛУЧАЙНЫЙ ВЕКТОР
Замечание. По частным плотностям распределения вероятностей случайных
величин и в общем случае нельзя восстановить плотность распределения
случайного вектора ( , ) , так как частные плотности распределения не являются
исчерпывающими характеристиками, однако существуют частные случаи.
Пусть одна из компонент стремится к бесконечности
F
2... n
( х 2 ,..., х n ) F ( , x 2 ,..., x n )
1
n 1F ... ( x 2 ,..., x n )
2
n
x 2 .... x n
n
xn
... P (u , u
р ... ( x 2 ,..., x n )
2
1 x 2
2
,...,u n )du1du 2 ...du n
р (u 1 , x 2 ,..., x n )du
Правило нахождения частных функций распределении для n-1 компонент
р (x i )
i
F ( x i )
i
x i
р (u 1 ,...u i 1 , x i , u i 1 ..., u n )du1 ...du n
40

41.

СЛУЧАЙНЫЙ ВЕКТОР: УСЛОВНЫЙ ЗАКОН
РАСПРЕДЕЛЕНИЯ
Условным законом распределения одной из одномерных составляющих
двумерной случайной величины ( , ) называется ее закон распределения,
вычисленный при условии, что другая составляющая приняла определенное
значение (или попала в какой-то интервал).
Условное распределение СВ при условии, что СВ x ( приняла значение
х), задается с помощью условных вероятностей:
p ( y / x )
P[( x )( y)]
P( x )
Условное распределение СВ при условии, что y задается с помощью
условных вероятностей:
P[( x)( y )]
P( y )
Вероятности p ( x / y ) этого распределения будут условными
вероятностями события x , найденными в предположении, что событие y
p ( x / y )
произошло.
41

42.

СЛУЧАЙНЫЙ ВЕКТОР: УСЛОВНЫЙ ЗАКОН
РАСПРЕДЕЛЕНИЯ
В случае непрерывных случайных величин необходимо определить
плотности вероятности условных распределений.
Пусть ( , ) непрерывный (дискретный) случайный вектор с плотностью
распределения р ( x, y) и р ( x ) - плотность распределения случайной
компоненты.
Условной плотностью распределения случайной величины при условии,
что случайная величина приняла значение х, называется отношение:
р ( y / x )
р (x, y)
р ( x , y)
р ( x )
р (x, y)dy
Аналогично определяется условная плотность вероятности при = y:
р i ( x / y)
р (x, y)
p ( y)
р ( x, y)
р ( x, y)dx
р (x, y) р (x) р ( y / x) р ( y) р (x / y)
Соотношение
называются формулой умножения плотностей распределения вероятностей,
согласно которой совместная плотность распределения случайного вектора ( , )
представима в виде произведения условной плотности одной случайной величины
на безусловную плотность другой случайной величины.
42

43.

ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
Случайные величины 1 , 2 ,..., n называются независимыми, если для любых
измеримых множеств А1,А2,…,Аn имеет место равенство
Р 1 А1 , 2 А 2 ,..., n А n P 1 A1 * ... * P n A n (1)
В дальнейшем для простоты рассматриваем двумерную случайную
величину (непрерывную или дискретную).
Теорема 1.(первый критерий независимости СВ) Случайные величины и
называются независимыми тогда и только тогда, когда х и y выполнено любое из
равенств:
F ( x, y ) F ( x) F ( y ) (2)
р (x, y) р (x) р ( y) (3)
В противном случае, при невыполнении равенства случайные величины и
называются зависимыми.
Пояснение. Рассматриваем непрерывный случайный вектор. Пусть А1 множество из
– бесконечности до х, а А2 от – бесконечности до у, получим выражение (2) (так как
мы рассматриваем вероятность того, что кси будет меньше х, а этта меньше у).
Дифференцируя (2) получим (3), а интегрируя (3) по х принадлежащему А1 и у
принадлежащему А2, где А1 и А2 произвольные множества, получим (1), другими
словами ищем вероятность попадания.
43

44.

ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ
Теорема 2.(второй критерий независимости СВ) Случайные величины и
независимы тогда и только тогда, когда для любых их возможных значений (х,у)
выполняется одно из соотношений:
р ( y / x) р ( y) и р (x / y) р (x)
Независимость двух случайных величин и означает, что условные плотности
вероятности каждой из них совпадают с соответствующими «безусловными»
плотностями, т.е. f y ( x) f1 ( x) и f x ( y) f 2 ( y)
44

45.

ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ: ПРИМЕР
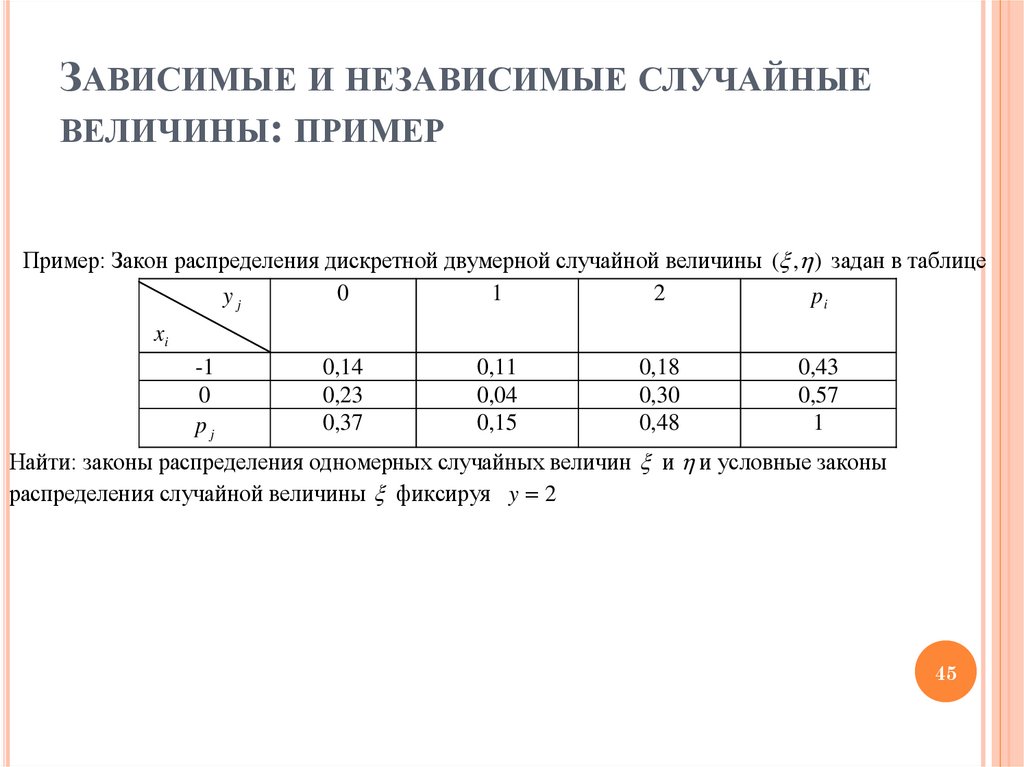
Пример: Закон распределения дискретной двумерной случайной величины ( , ) задан в таблице
0
1
2
pi
yj
xi
-1
0
pj
0,14
0,23
0,37
0,11
0,04
0,15
0,18
0,30
0,48
0,43
0,57
1
Найти: законы распределения одномерных случайных величин и и условные законы
распределения случайной величины фиксируя y 2
45

46.

ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ: ПРИМЕР
1. Случайная величина может принимать значения:
1 с вероятностью p1 0.14 0.11 0.18 0.43
0 с вероятностью p2 0.23 0.04 0.30 0.57 , т.е. ее закон распределения :
-1
0
xi
0,43
0,57
pi
Аналогично закон распределения :
0
1
2
yj
0,37
pj
0,15
0,48
2. Условный закон распределения при фиксированном y 2 , получим если вероятности pij ,
стоящие
в
предпоследнем
столбце
таблицы,
разделим
на
их
сумму,
P[( 1)( 2 j )] 0.18 18
p ( x / 2)
0.38
P( 2)
0.48 48
P[( 0 i )( 2)] 0.30 30
p ( x / 2)
0.63
P( 2 j )
0.48 48
Получим: 2 :
xi
-1
0
p ( x / 2)
0,38
0,63
46