Similar presentations:
Теорема об отрезках пересекающихся хорд
1. Теорема об отрезках пересекающихся хорд
2.
ПРОВЕРЯЕМ ДОМАШНЕЕ ЗАДАНИЕ3.
4.
5. ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ самостоятельная работа выполнить в тетрадке (чертить не надо, записать только номер задания и ответ)
6.
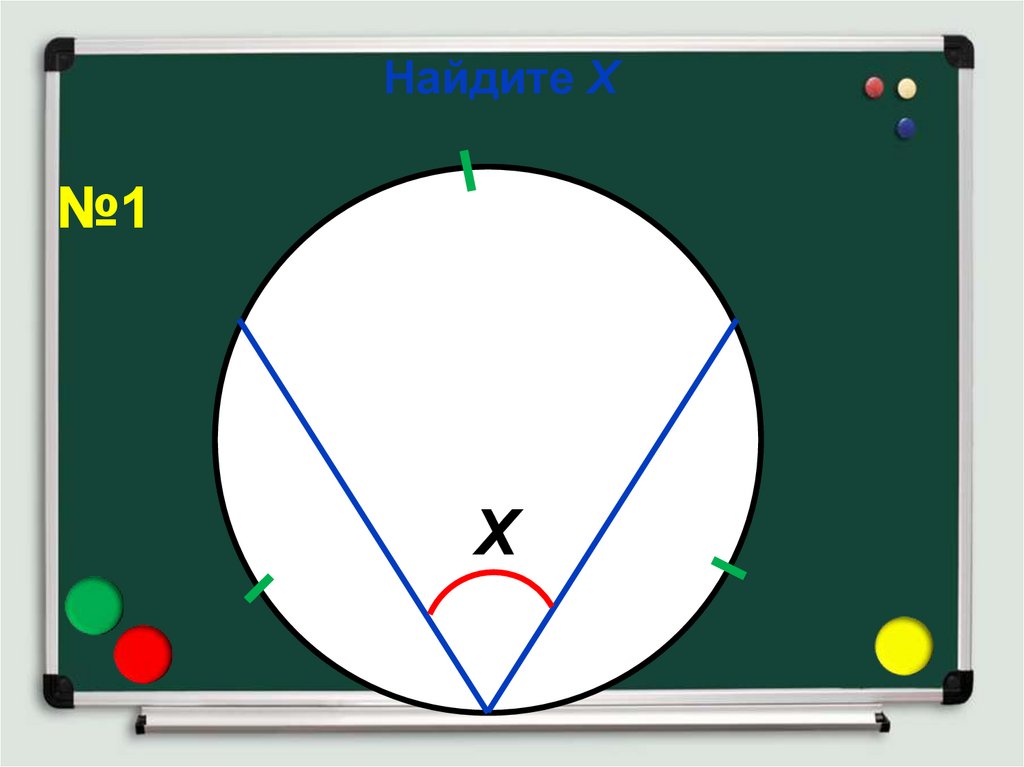
Найдите Х№1
Х
7.
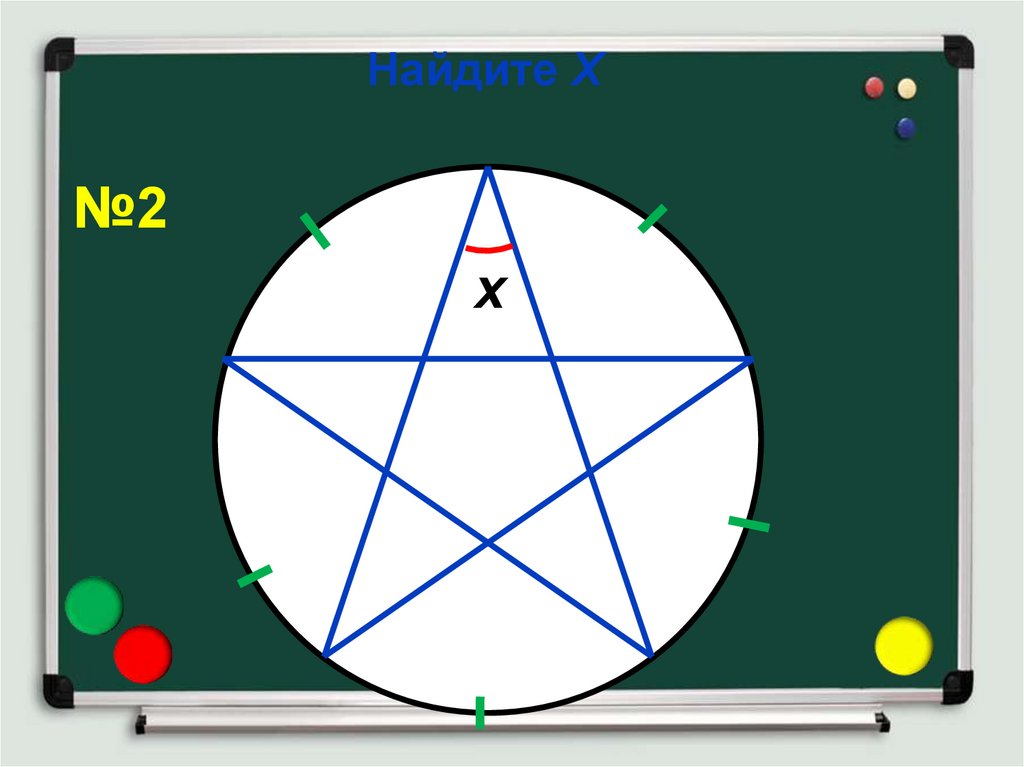
Найдите Х№2
x
8.
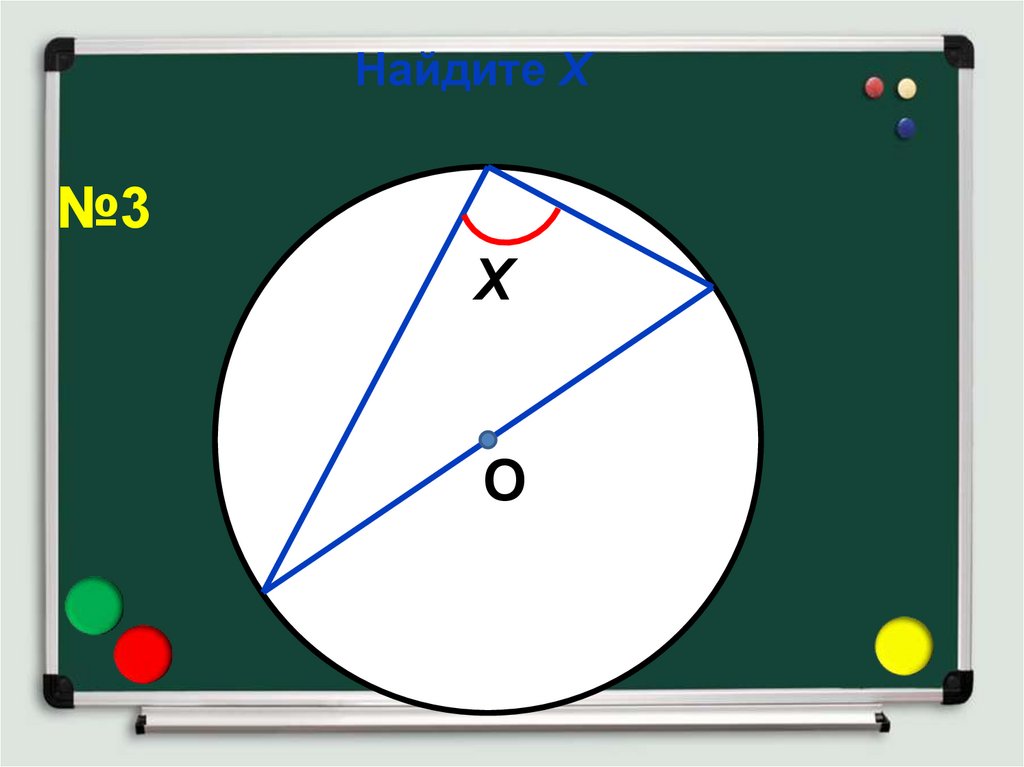
Найдите Х№3
Х
О
9.
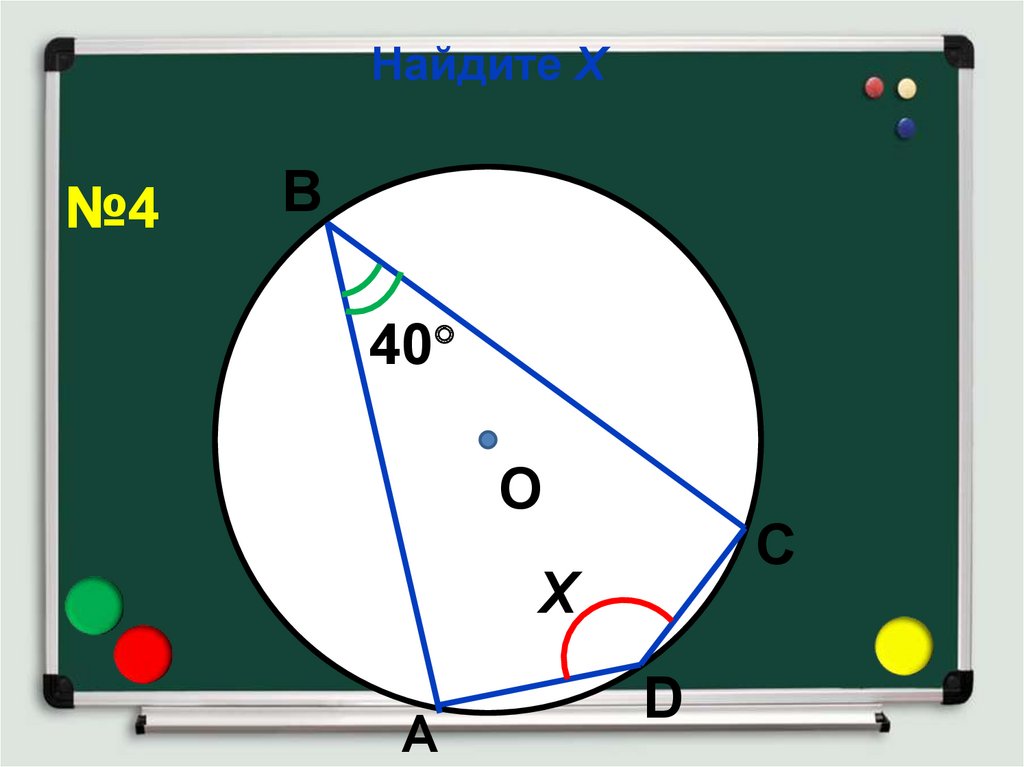
Найдите Х№4
В
40
О
С
Х
А
D
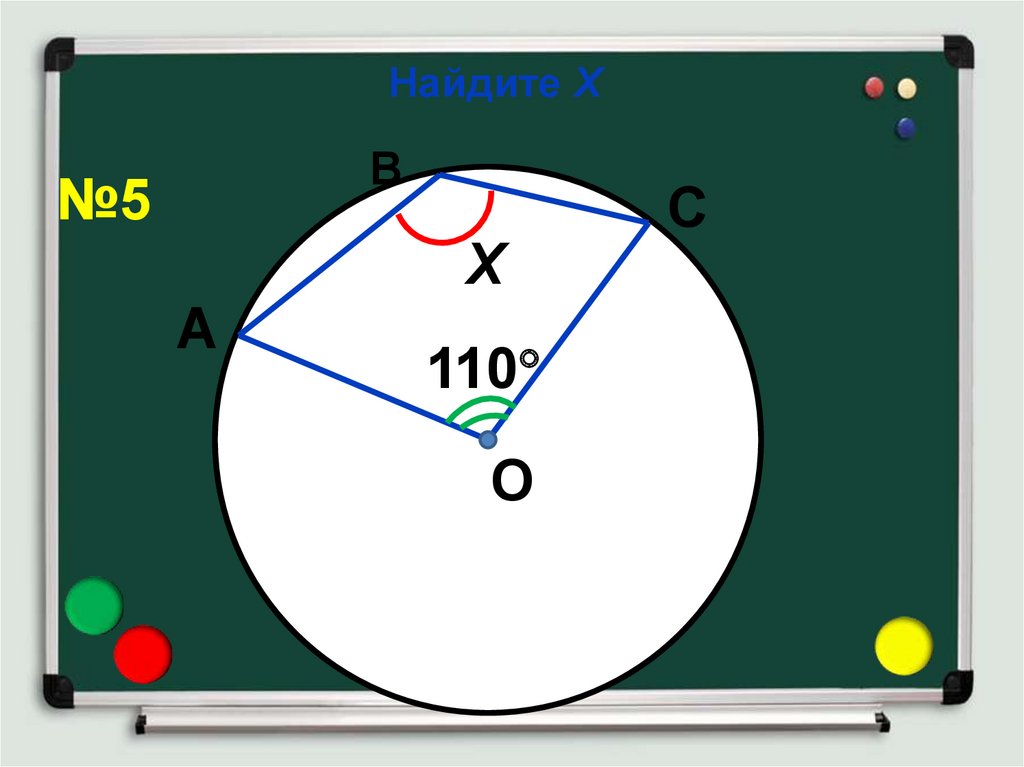
10. Найдите Х
В№5
Х
А
110
О
С
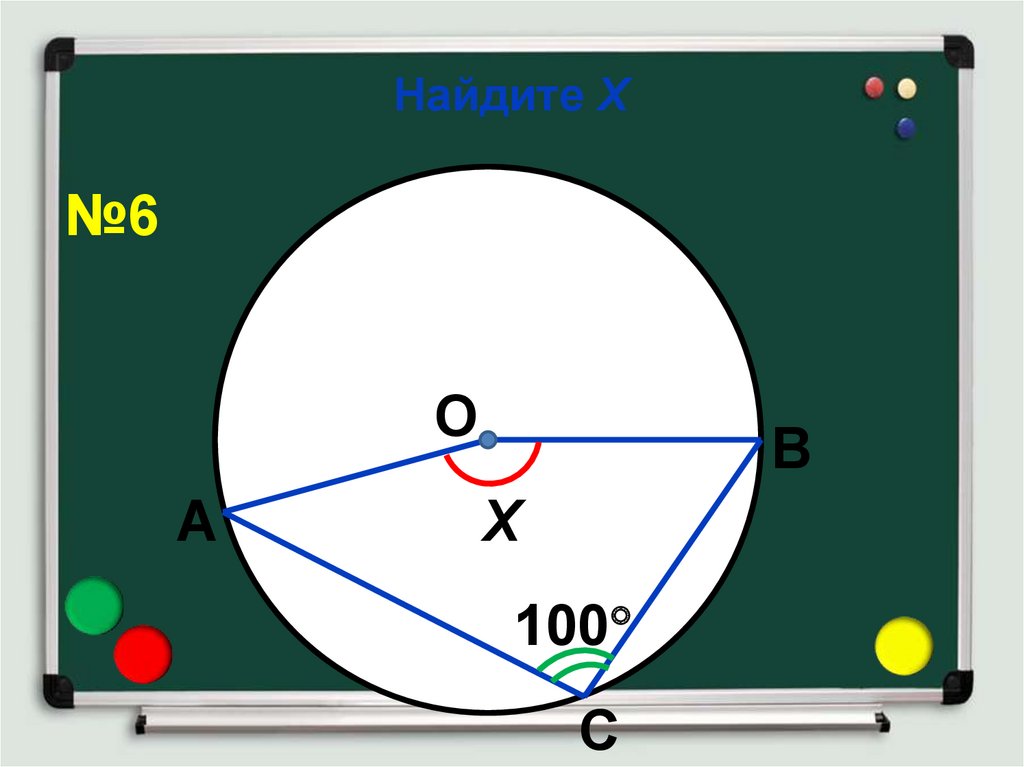
11. Найдите Х
№6О
А
В
Х
100
С
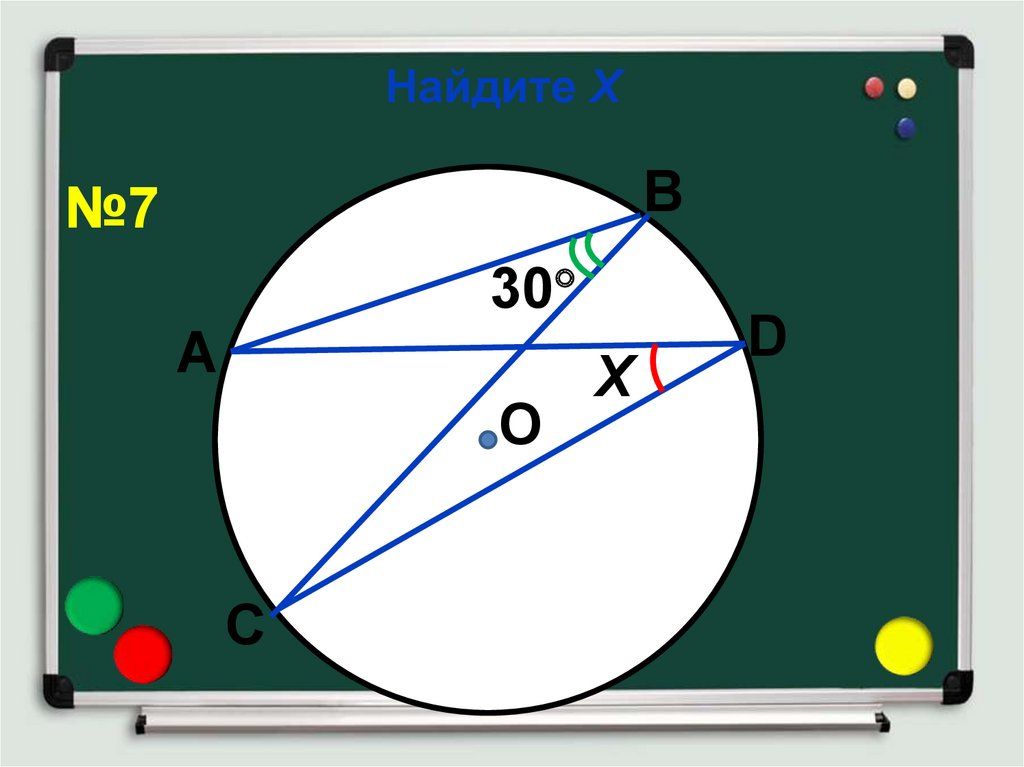
12. Найдите Х
В№7
30
А
О
С
Х
D
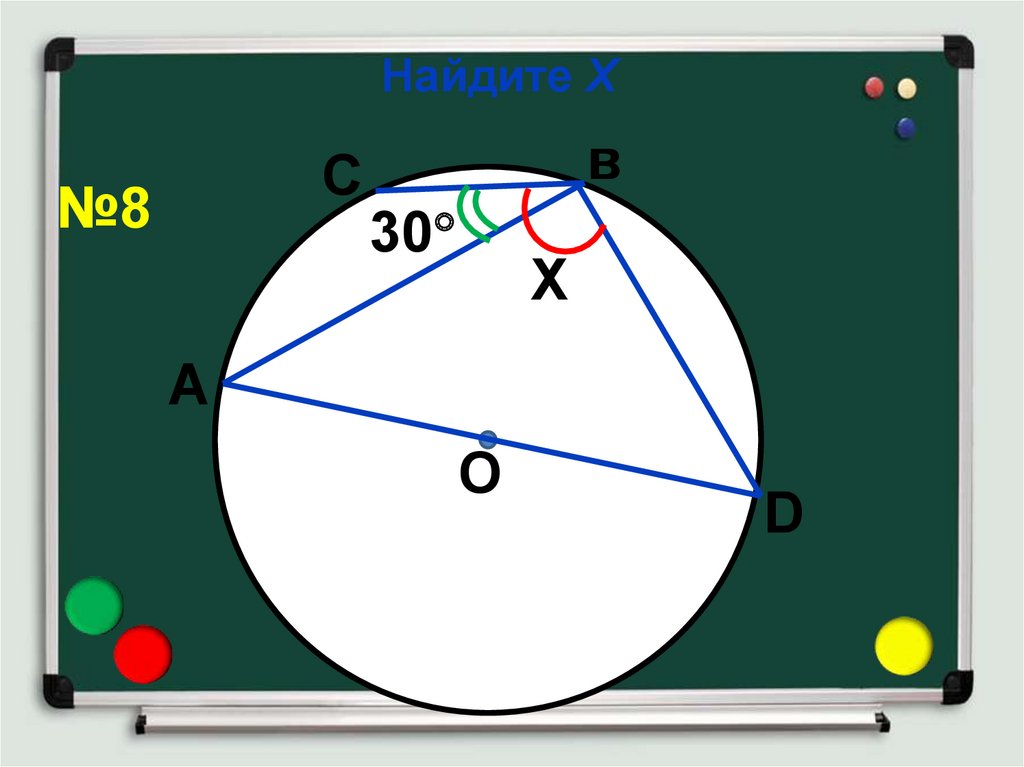
13. Найдите Х
вС
№8
30
Х
А
О
D
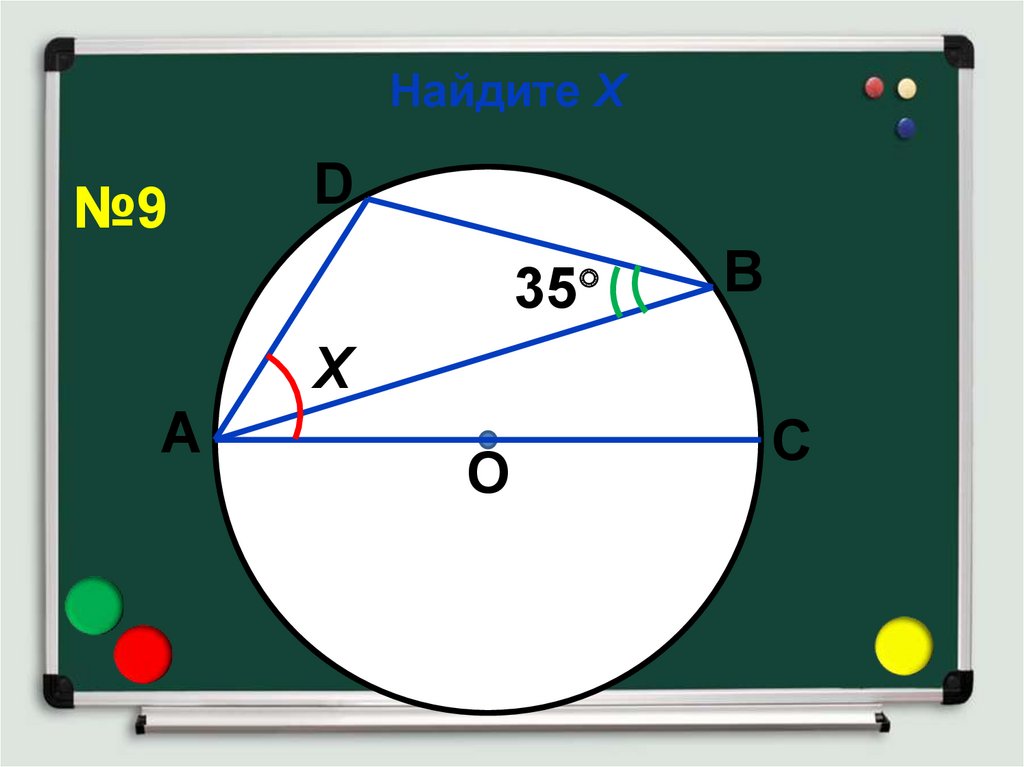
14. Найдите Х
№9D
35
В
Х
А
О
С
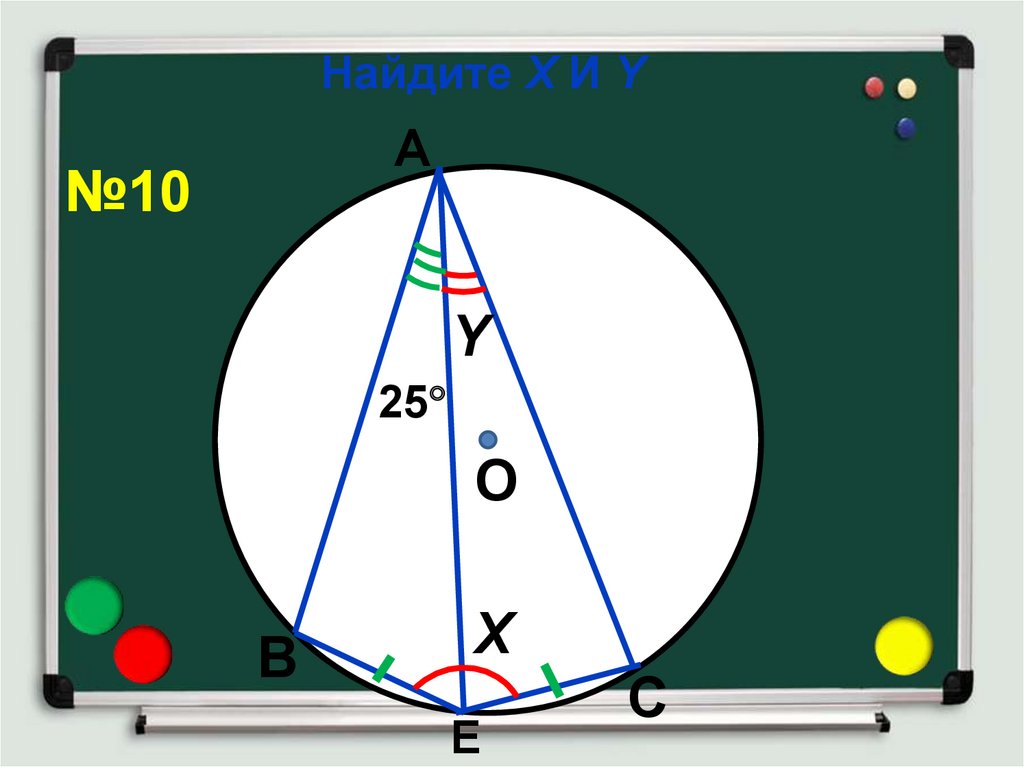
15. Найдите Х И Y
А№10
Y
25
О
В
Х
Е
С
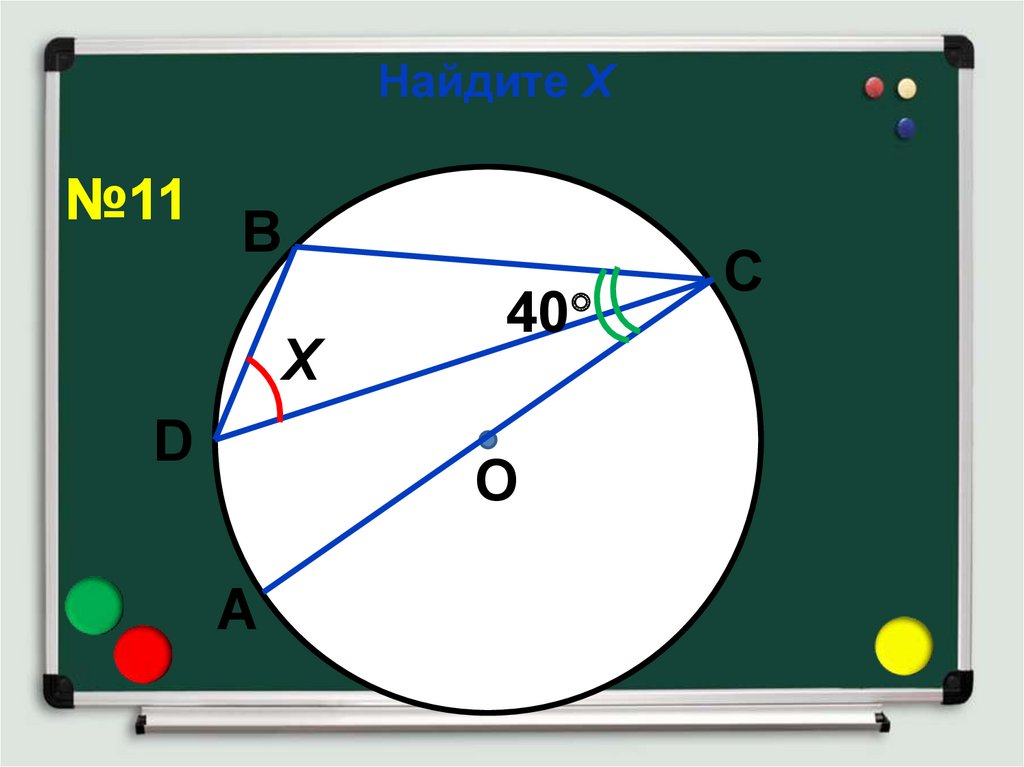
16. Найдите Х
№11В
Х
D
40
О
А
С
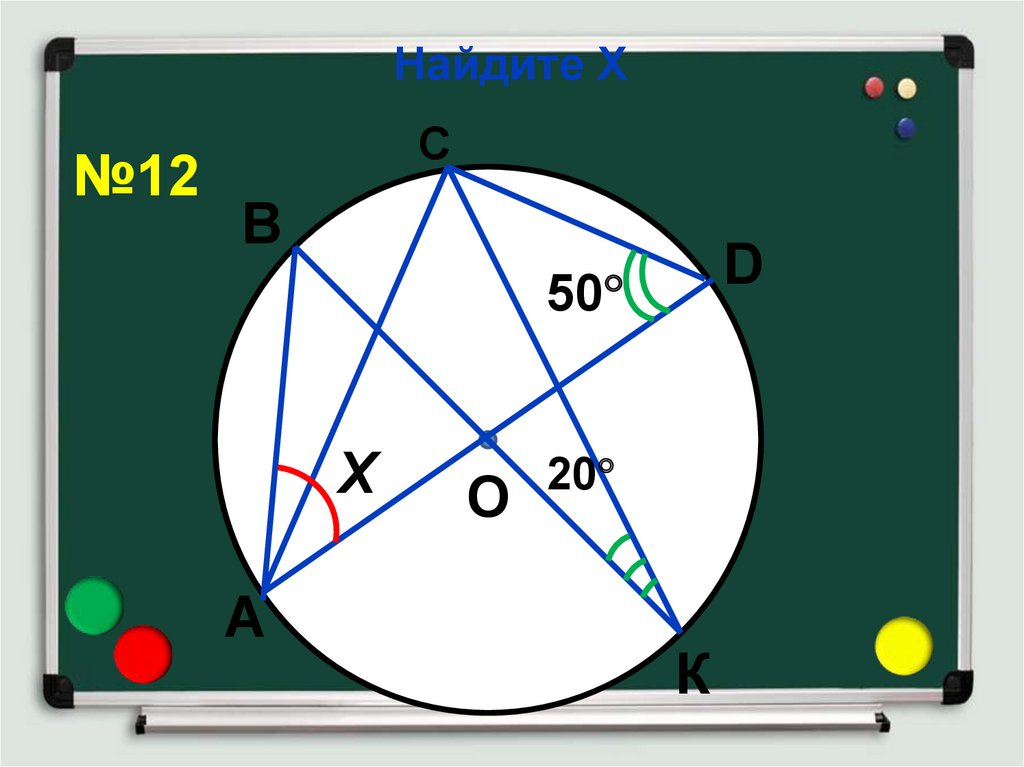
17. Найдите Х
№12С
В
D
50
Х
А
О
20
К
18.
Задача: Найти АЕ , если ВЕ=4 см, DE = 6 см ,СЕ=2см.Доказать , треугольник АЕС подобен треуголь нику DBE.
Решение.
АЕС подобен
DEB т.к.
А
угол AED и угол ABD вписанные и
опираются на одну дугу. Угол AEC
И угол DEB равны как вертикальные
( первый признак подобия), отсюда
Стороны треугольников пропорциональны
AE : ED = BE: CE, AE : 6= 4: 2
C
отсюда АЕ = 6 * 4 :2 =12см.
D
Е
В
19.
Задача : Докажите , что если две хорды AB иCD окружности пересекаются в точке Е , то
АЕ * ВЕ =СЕ *DE.
C
А
2
1
E
D
Доказательство :
Рассмотрим треугольники ADE и
СВЕ. на Углы 1 и 2 равны, т. к
B они вписанные и опираются на
одну и ту же дугу BD . Углы 3 и 4
равны как вертикальные.
Следовательно треугольники
подобны по первому признаку.
Отсюда AE : CE =DE: BE или
AE *BE=CE*DE.
20.
а.
СТР 170 ТЕОРЕМА
План-конспект доказательства теоремы.
1) треугольники АСЕ и DBE подобны т. к
угол А равен углу D как вписанные углы ,
опирающиеся на дугу ВС , углы AEC и DEB
равны как вертикальные.
2) AE:DE= CE:BE
3) AE*BE= CE*DE.
21.
Домашнее задание:Стр.167 П.71 , стр.184
вопрос14, № 666(б), № 671(б)
22.
УСПЕХОВВ
УЧЕБЕ










 mathematics
mathematics