Similar presentations:
Теорема об отрезках пересекающихся хорд
1.
Классная работа 10.04.182.
1. Закончите предложение:1) Угол называется центральным, если …
2) Угол называется вписанным, если …
3) Центральный угол измеряется …
4) Вписанный угол измеряется …
5) Вписанные углы равны, если …
6) Вписанный угол, опирающийся на
полуокружность …
3.
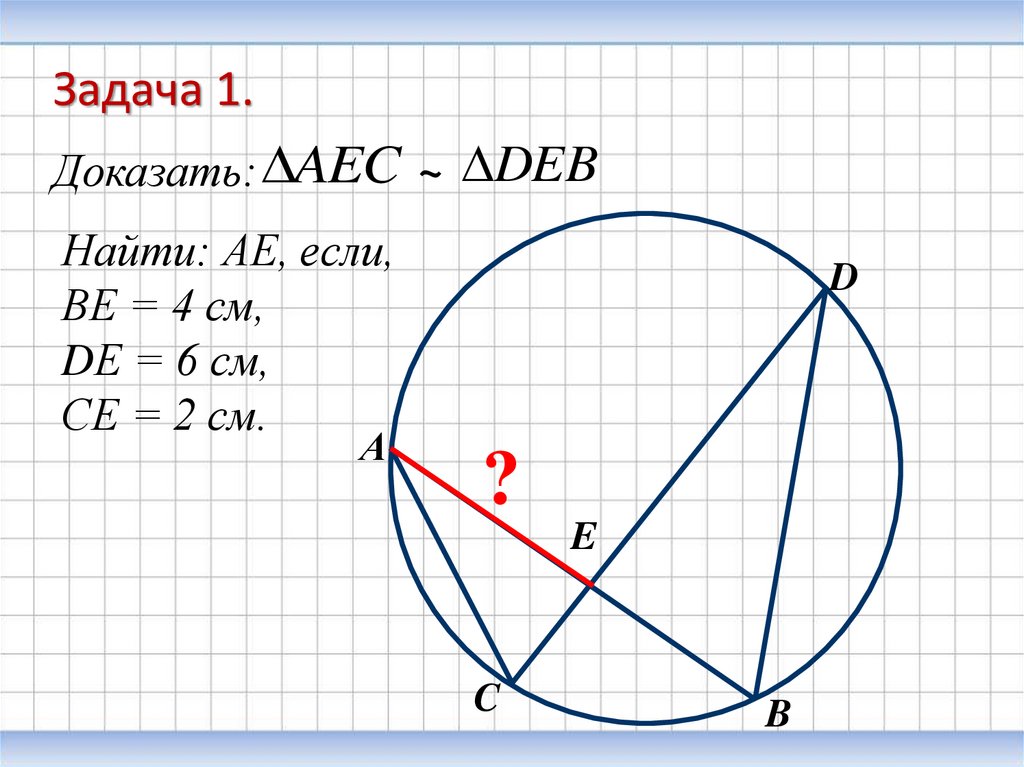
Задача 1.Доказать: AEC ~ DEB
Найти: АЕ, если,
ВЕ = 4 см,
DЕ = 6 см,
СЕ = 2 см.
А
D
?
E
C
B
4.
Вопросы для обсуждения.Что вы можете сказать об углах CAB и CDB?
Об углах AEC и DEB?
Какими являются треугольники ACE и DBE?
C
Чему равно отношение их
сторон, являющихся
отрезками хорд
А
E
касательных?
Какое равенство можно
записать из равенства двух
отношений , используя
основное свойство пропорции?
D
B
5.
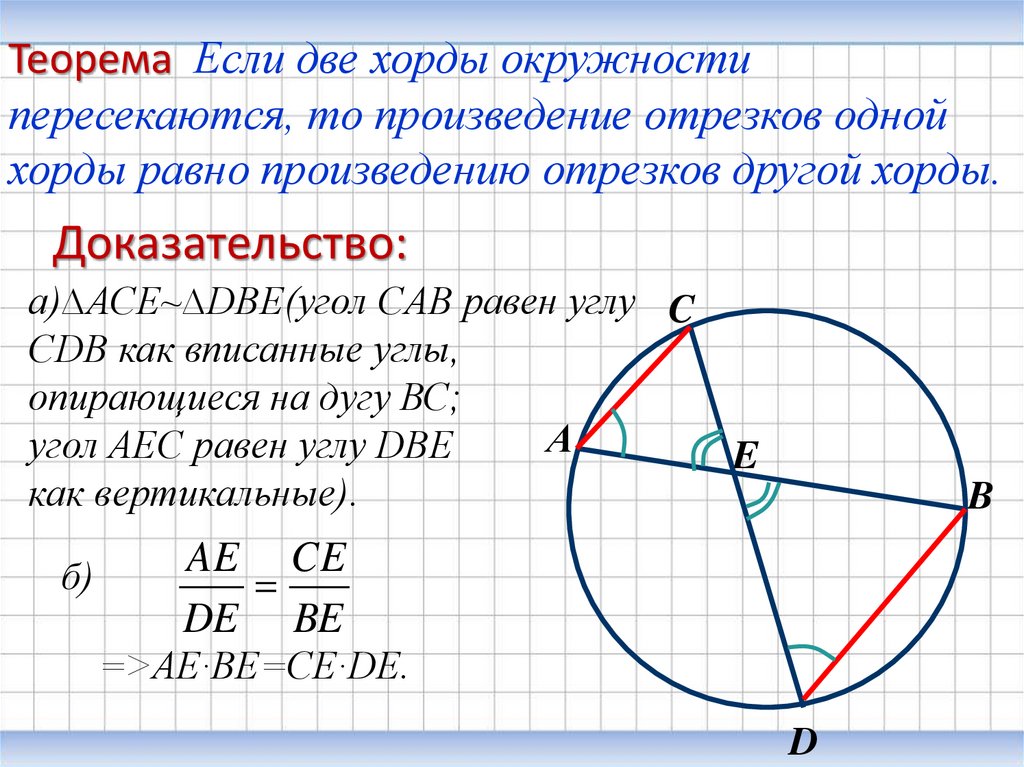
Теорема Если две хорды окружностипересекаются, то произведение отрезков одной
хорды равно произведению отрезков другой хорды.
Доказательство:
а)∆АСЕ~∆DВЕ(угол CAB равен углу C
CDB как вписанные углы,
опирающиеся на дугу ВС;
А
угол АЕС равен углу DBE
E
как вертикальные).
б)
B
AE CE
DE BE
=>АЕ∙ВЕ=СЕ∙DE.
D
6. Задачи из учебника
№667№670
№666
(а)- краткое
решение
№671 (а) – краткое
решение
7. Домашнее задание
П.72№660,
671 (1)
666(б,в), 668,





 mathematics
mathematics