Similar presentations:
Дифференциальные уравнения высших порядков
1.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯВЫСШИХ ПОРЯДКОВ
F ( х, y , y , у ) 0
y f ( x, y , у )
y ( x0 ) y0 , y ( x0 ) y0 , x0 , y0 , у0 const
y (x)
y ( x, C1 , С2 ) :
С
y ( x, C , С )
0
1
С
0
2
0
1
0
2
2.
ПОНИЖЕНИЕ ПОРЯДКА ДИФФЕРЕНЦИАЛЬНЫХУРАВНЕНИЙ
1.
y f ( x )
y f ( x )dx F ( x ) C1
y ( F ( x ) C1 )dx C2
3.
2. F ( х, y , y ) 0y p y p
y p
F
(
y
,
p
,
p
) 0
4.
3. F ( y , y , y ) 0y p p( y )
y ( p( y )) p ( y ) y ( x ) p p
y p
F
(
y
,
p
,
p
p
) 0
F ( x, ty , ty , ty ) t F ( x, y , y , y )
k
5.
Примеры: Решить уравнения:1
1) y
x sin x
2
1 x
1
y
x
sin
x
dx
2
1 x 2
x
y arctgx
cos x C1
2
2
x
y arctgx
cos x C1 dx
2
6.
31
x
2
y xarctgx ln(1 x ) sin x C1 x C2
2
6
2) y ( e sin 3x ) x,
2x
y (0) 1, y (0) 1.
y ( e sin 3x ) xdx
2x
u x
du dx
dv ( e 2 x sin 3x )dx v 1 e 2 x 1 cos 3x
2
3
7.
1 2x 11 2x 1
y x e cos 3x e sin 3x C1
3
9
2
4
1 2x 1
1 2x 1
y x e cos 3x e sin 3x C1 dx
3
9
4
2
1 2x 1
1 2x 2
y x e sin 3x e cos 3x C1 x C2
9
27
4
4
1
1
C
1
4
1 1 2 C2
4 27
5
C
1
4
143
C2
108
8.
5143
1 2x 1
1 2x 2
yч x e sin 3x e cos 3x x
9
27
4
108
4
4
3)
y y ctgx 2 x sin x,
y 1, y 0 при x .
4
y p, y p
p pctgx 2 x sin x,
p u v, p u v v u
9.
u v v u uv ctgx 2 x sin xu v u( v v ctgx ) 2 x sin x
v v ctgx 0
dv
ctgxdx
0
v
ln | v | ln | sin x | v sin x
u sin x 2 x sin x
u 2 x
u x C1
2
10.
p u v ( x C1 ) sin x2
y ( x C1 ) sin x
2
y ( x C1 ) sin xdx
2
y ( x C1 ) cos x 2 x sin x 2 cos x C2
2
C1
2
16
,
2
C2 1
2
2 2
11.
4)y tgy 2( y ) , y (1)
2
y p p( y )
p p tgy 2 p
4
, y (1) 2
y p p
2
p tgy 2 p
dp
cos y
2
dy
p sin y
2
2
p C1 sin y y C1 sin y
dy
C
dx
1
2
sin y
12.
ctg y C1 x C22 C1 sin
2
y C1 sin y
C1 4
4
ctg 4 C2 C2 3
4
yо arctg ( C1 x C2 )
yч arctg ( 4 x 3)
2
13.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯВТОРОГО ПОРЯДКА
y p( x ) y q( x ) y f ( x )
y p( x ) y q( x ) y 0
ЛДУ второго порядка с постоянными
коэффициентами
p ( x), q ( x) const y py qy f (x )
y py qy 0 (1)
yoo ( x) C1 y1 ( x) C2 y2 ( x)
14.
k pk q 02
(в уравнении (1) заменить у//, у/ и у на k2, k и k0)
Теорема:
Пусть k1 и k2 – корни характеристического уравнения.
Тогда общее решение уравнения (1) находится по
формуле:
1. к1 к2, общее решение уравнения (1) имеет вид:
k1 x
k2 x
уоо C1e C2e
2. к1=к2 , общее решение уравнения (1) имеет вид:
уоо C1e k1x C2 хe k2 x
3. к1 и к2 – комплексно– сопряженные корни, к1,2= i.
В этом случае общее решение уравнения (3) имеет
вид:
уоо е х (C1 Cos x C2 Sin x )
15.
Примеры: Найти общее решениеуравнения:
1) 2 у 3 у у 0
2k 2 3k 1 0
1
k1 1, k2
2
2) 4 у 4 у у 0
уоо C1e x C2e
1
x
2
4k 2 4k 1 0
1
k1 k2
2
уоо C1e
1
x
2
C2 хe
1
x
2
16.
3) 2 у у 3 у 02k 2 k 3 0
D 23
k1, 2
1 23i
1
23
i
4
4
4
1
23
,
4
4
уоо е
1
х
4
23
23
C1 Cos
x
C
Sin
x
2
4
4
17.
ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕУРАВНЕНИЯ (ЛНДУ) ВТОРОГО ПОРЯДКА С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
y py qy f (x ) ( 2)
yoн yoo yч
2
y py qy 0
k pk q 0 (3)
х
1 случай. f ( x ) е Рn ( х )
Рn(x) – многочлен степени n
а) - не корень уравнения (3), то
х
yч е Qn (x )
Qn(x) – многочлен степени n с
неизвестными коэффициентами
18.
б) - корень уравнения (3) кратности k, тоk х
yч х е Qn (x )
Если f ( x ) Рn ( х ), то 0, yч Qn (x )
( - не корень уравнения (3) )
yч х Qn (x )
k
( - корень уравнения (3) кратности k)
19.
2 случай.х
f ( x ) е ( Рn ( х ) cos x Qm ( x ) sin x )
Рn(x), Qm(x) – многочлены степени n и m
N max(n, m )
а) i - не корни уравнения (3), то
х
уч е ( РN ( х ) cos x QN ( x ) sin x )
б) i - корни уравнения (3) кратности k,
то
k х
уч х е ( РN ( х ) cos x QN ( x ) sin x )
20.
Если f ( x ) a cos x b sin x,т.е. m n 0,
уч А cos x В sin x
( i - не корни уравнения (3) )
уч х ( А cos x В sin x )
( i - корни уравнения (3))
21.
Теорема. Если уч1 и уч2 – частные решенийy py qy f1 ( x )
и
y py qy f 2 ( x ),
то функция уч= уч1 + уч2 – частное решение
уравнения
y py qy f1 ( x ) f 2 ( x )
22.
Примеры: Найти общее решениеуравнения:
y 7 y 5 xе
2
k 7k 0
k1 0 k2 7
х
1)
х
f ( x ) е Рn ( х ) 5 хе
Р1 ( х ) 5 х, 1
уоо C1 C2e
7x
х
yч е Q1 ( x ) е ( Аx В )
х
х
y ч е ( Аx В ) Ае е ( Аx В А)
/
х
х
х
23.
y ч е ( Аx В А) Аех
е ( Аx В 2 А)
//
х
х
е ( Ах 2 А В ) 7е ( Ах А В ) 5 xе
х
х
х
6 Ах 5 А 6 В 5 x
6 А 5
5 А 6 В 0
5
25
5
25
х
А , В
уч е x
6
36
36
6
24.
255
уон С1 С2е е x
36
6
7х
2)
х
3 х
y 6 y 9 у ( x 2)е
2
k 6k 9 0
k1, 2 3
уоо (С1 С2 х )е
3 х
3 х
х
f ( x ) ( x 2)е е Рn (х )
Р1 ( х ) х 2, 3
2 3 х
yч х е Q1 ( x ) х 2е 3 х ( Аx В )
25.
yч е3 х
(3 Аx 2 Вх 3 Ах 3Вх )
yч е
3 х
(9 Аx 18 Ах 9 Вх 6 Ах
/
//
2
3
3
2
2
2
12 Вх 2 В )
6 А 1
1
А , В 1
6
2 В 2
2 3 х 1
уч х е x 2
6
3 х
3 х 2 1
уон (С1 С2 х )е е х x 2
6
26.
3)y 3 y 2 у ( 2 x 3) sin x cos x
2
k 3k 2 0
k1 1 k2 2
x
2 x
уоо C1e C2e
f ( x ) ( 2 x 3) sin x cos x
Q0 ( x ) 1 Р1 ( х ) 2 х 3
0, 1
уч РN ( х ) cos x QN ( x ) sin x
N max(1,0) 1
уч ( Aх B ) sin x (Cx D ) cos x
27.
121
3
3
А , В , C , D
5
25
5
25
21
3
1
3
уч х sin x x cos x
25
25
5
5
28.
213
1
3
уон х sin x x cos x
25
25
5
5
х
2 х
С1е С2е .
4) y 19 у 3x sin 4 x cos 4 x
2
k 16 0 k1, 2 4i
уоо C1 Cos 4 x C2 Sin 4 x
0, 4 Q0 ( x ) 1 Р1 ( х ) 3х
N max(1,0) 1
уч х (( Aх B ) cos 4 x (Cx D ) sin 4 x )
29.
3A , B C 0,
16
11
D .
64
11
3
уч х х cos 4 x sin 4 x
64
16
3 2
уон C1 cos 4 x C2 sin 4 x х cos 4 x
16
11
x sin 4 x
64
30.
5)y 2 у 5 y xe cos 2 x x x 2
2
k 2k 5 0
k1, 2 1 2i 1, 2
x
2
уоо e (C1 Cos 2 x C2 Sin 2 x )
x
y 2 у 5 y xe cos 2 x
2
y 2 у 5 y x x 2
x
уч1 e х (( Aх B ) cos 2 x (Cx D ) sin 2 x )
1
x 1
уч1 e х cos 2 x x sin 2 x
8
16
x
31.
уч 2 Aх Bx C2
1 2 1
38
уч 2 х x
5
25
125
уон уоо уч1 уч 2
уон e (C1 Cos 2 x C2 Sin 2 x )
x
1
1
e х cos 2 x x sin 2 x
8
16
1 2 1
38
х
x
.
5
25
125
x



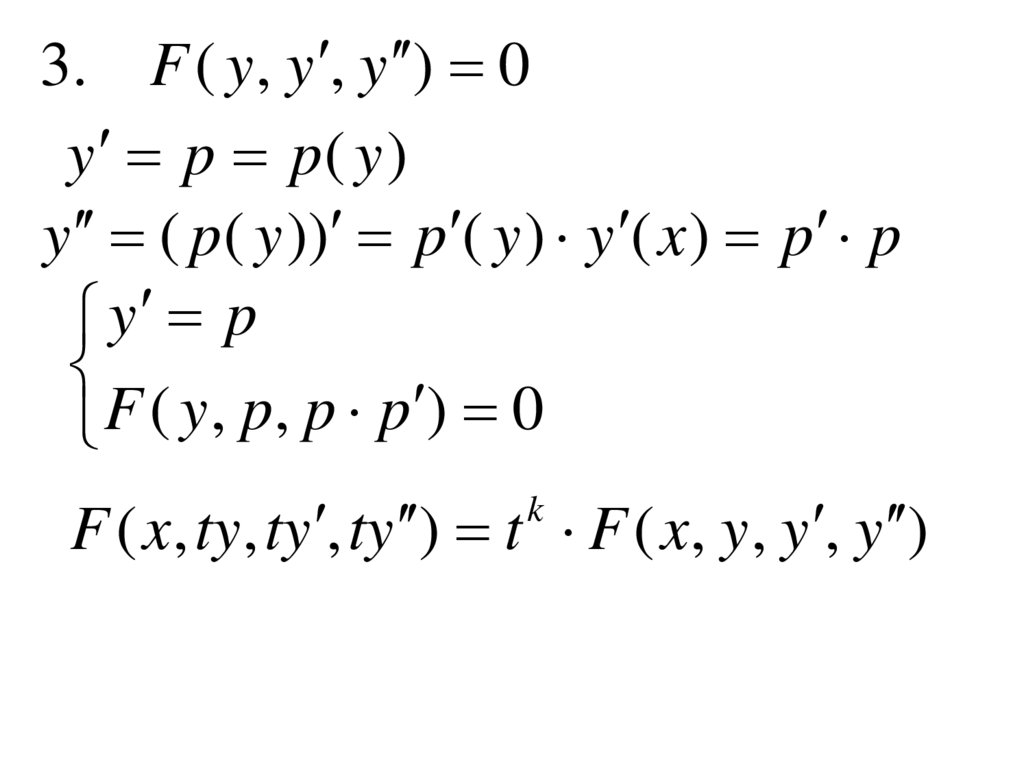




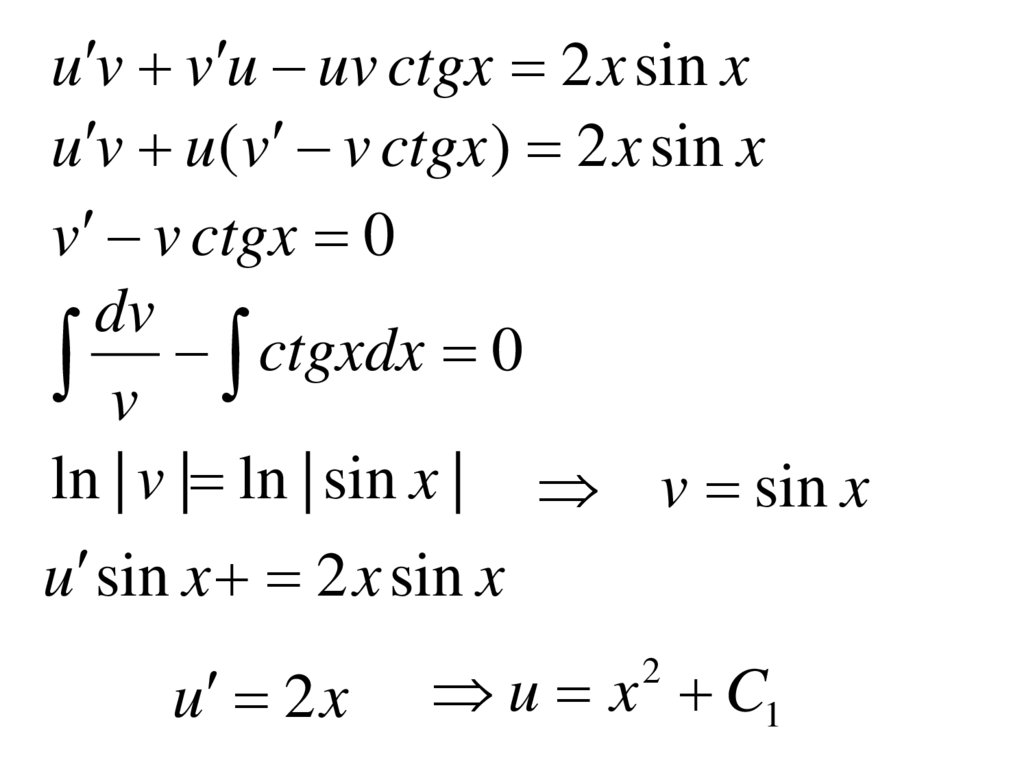

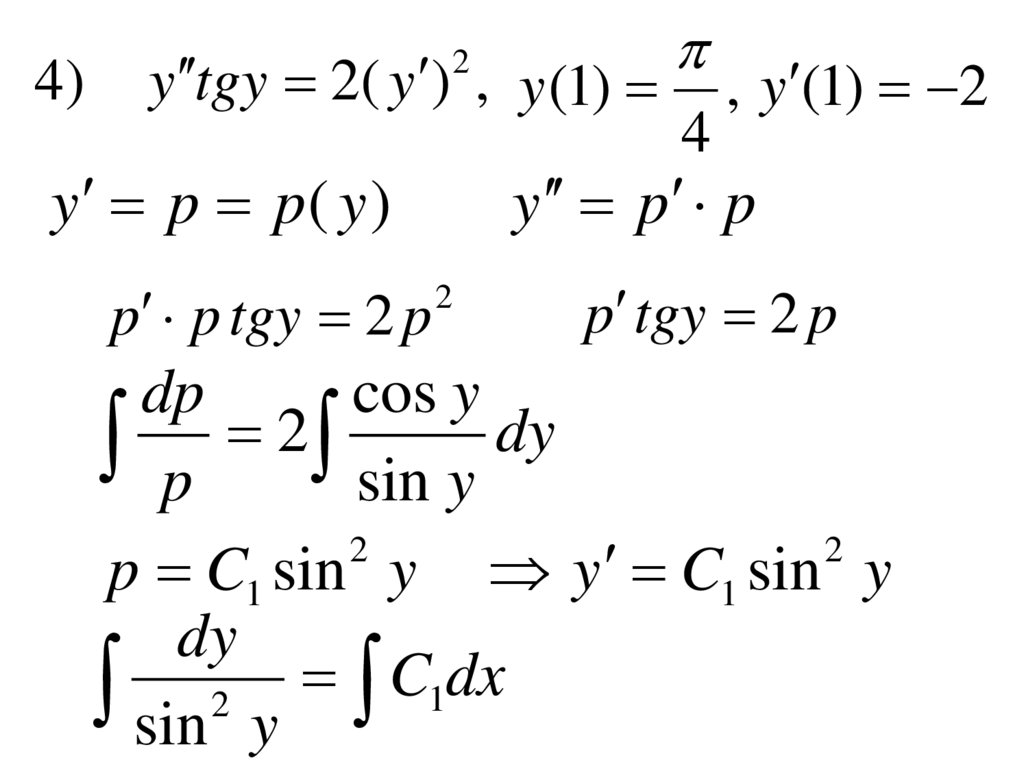












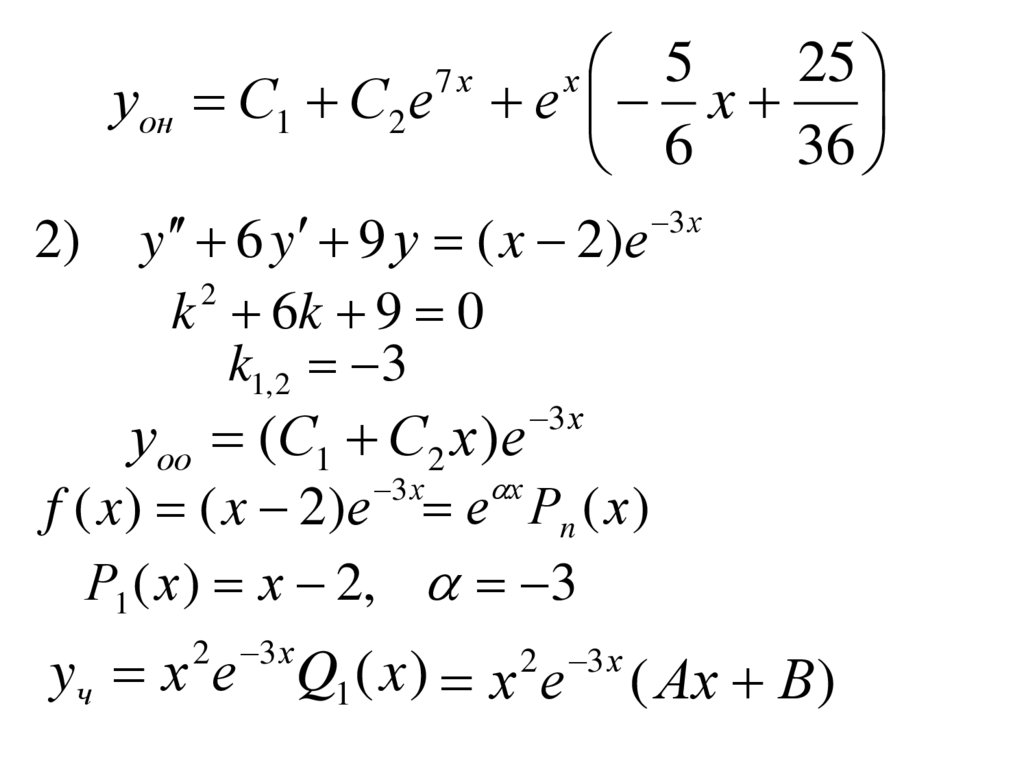
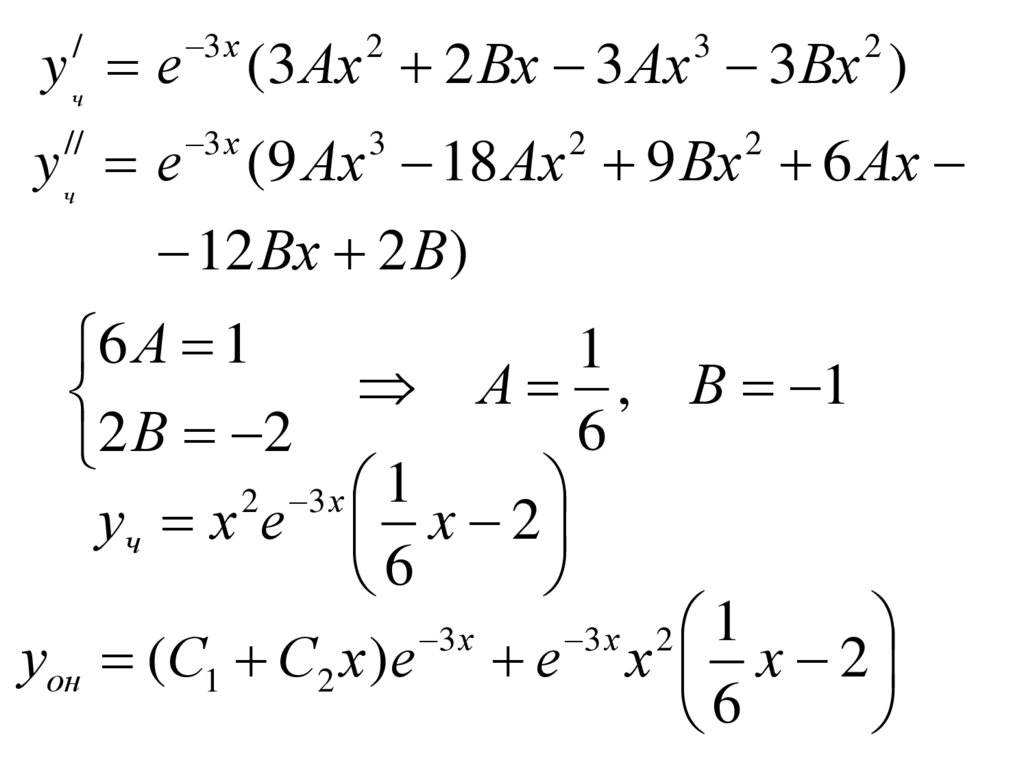
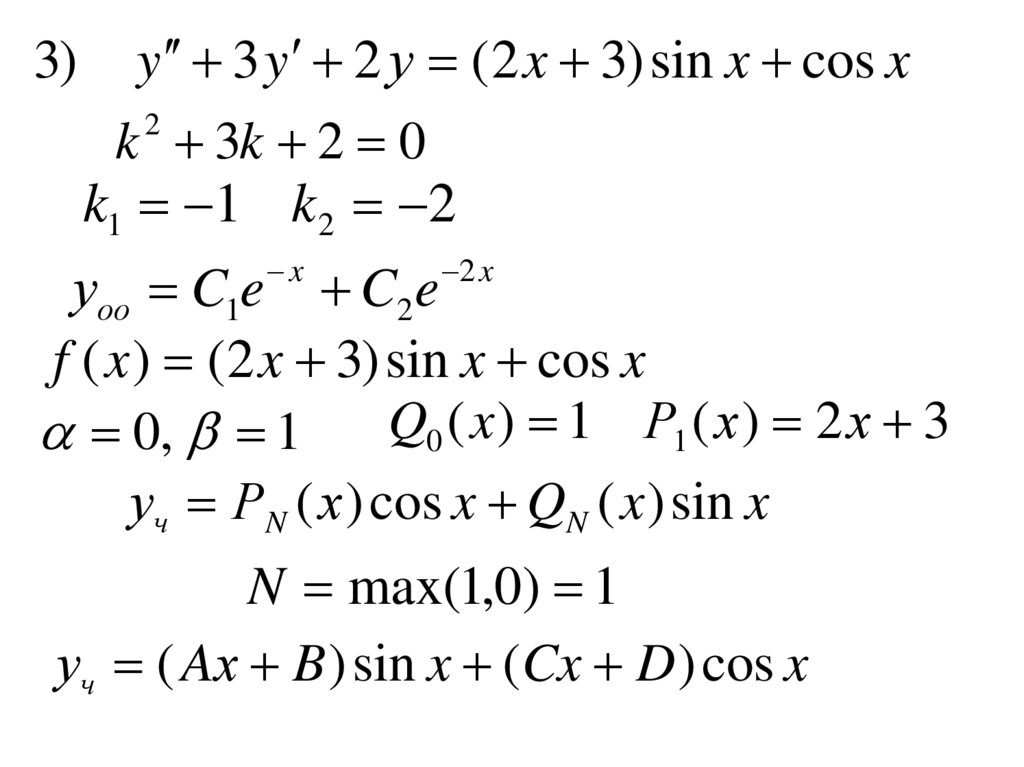
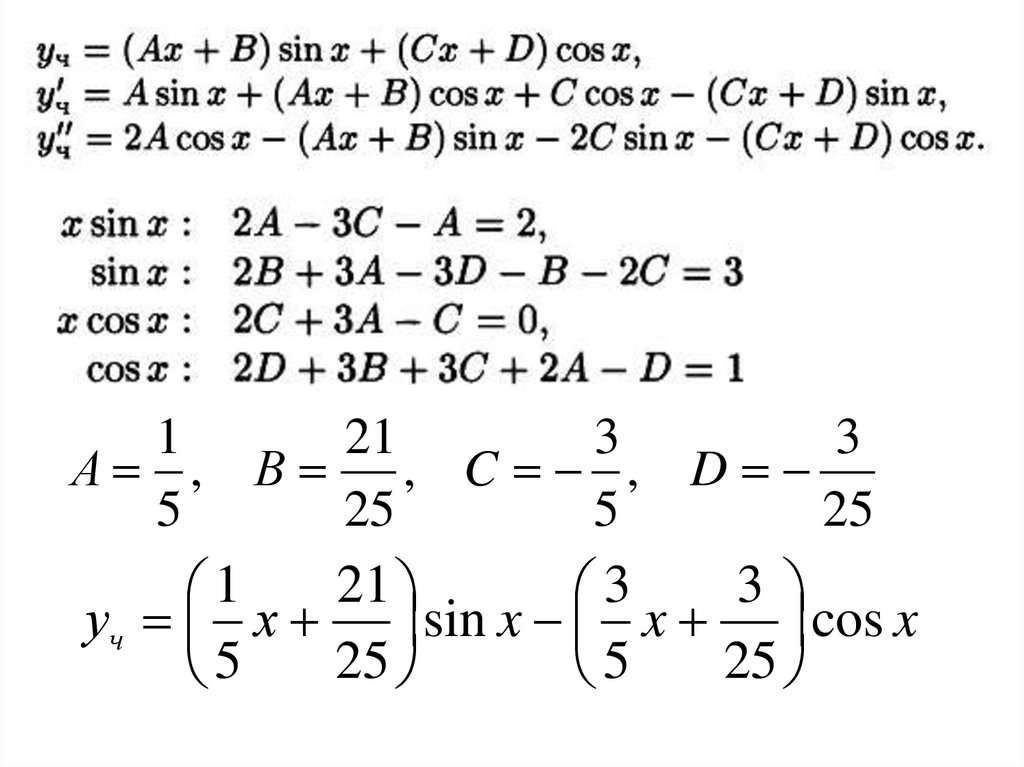
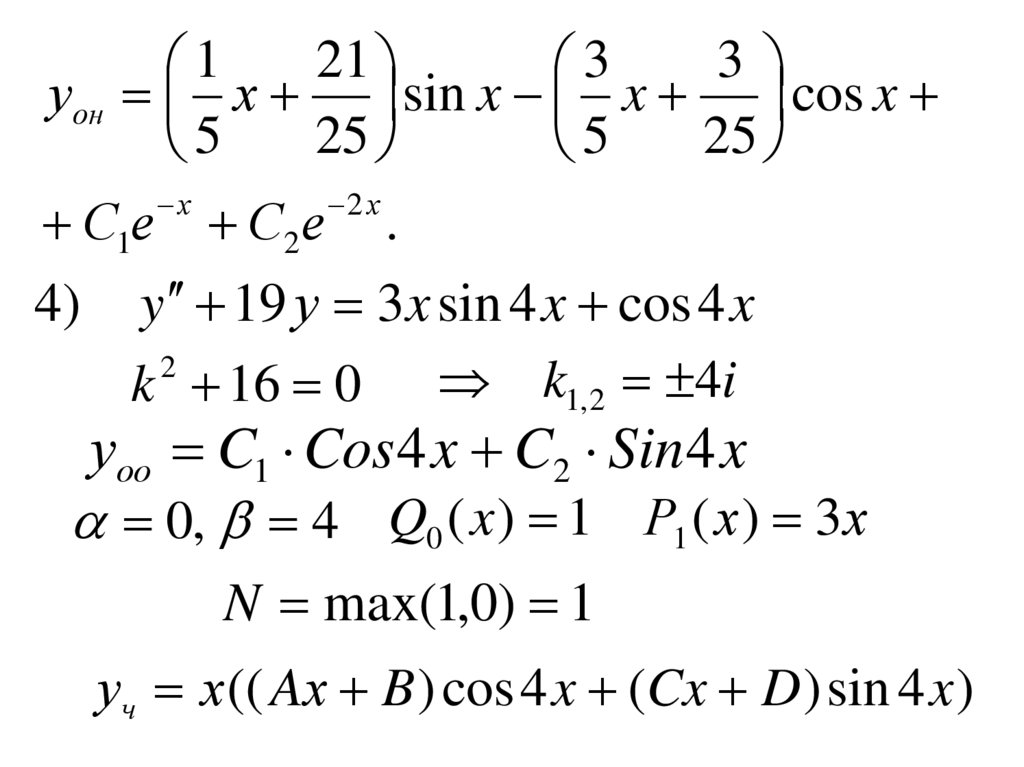

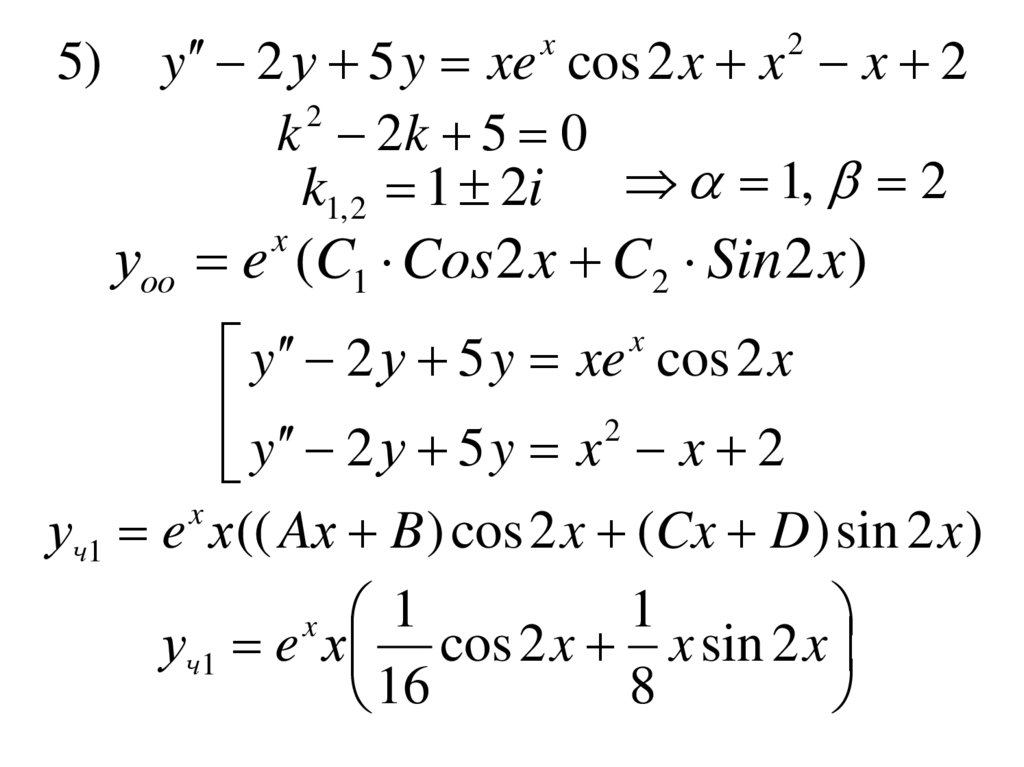

 mathematics
mathematics








