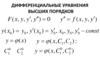Дифференциальные уравнения высших порядков. Приложения дифференциальных уравнений в экономике. Лекция №15

1.

Дисциплина: МАТЕМАТИКА
Раздел 4: Дифференциальные уравнения
Лекция №15
Дифференциальные уравнения высших порядков.
Приложения дифференциальных уравнений
в экономике
Разработчик: Бредихина Ольга Александровна

2.

4.3 Дифференциальные уравнения высших порядков
4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Дифференциальное уравнение вида a y b y c y 0 , где
a, b, c – числа (причём a≠0), называется линейным
однородным дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Структура общего решения линейного однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами имеет вид
yoo C1 y1 C2 y 2 ,
где C1, C2 – числа, а y1=y1(x) и y2=y2(x) – частные решения,
образующие фундаментальную систему решений.
Фундаментальную систему y1 и y2 образуют в случае,
когда отношение y1 const.
y2

3.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Эйлером было предложено частное решение искать в виде
y=ekx, где k=const. Тогда y k e kx
, y k 2 e kx . Подставив
y, y , y в уравнение a y b y c y 0 , получим
a k 2 ekx b k ekx c ekx 0,
e kx a k 2 b k c 0.
Из последнего уравнения получим a k 2 b k c 0 , это
равенство называется характеристическим уравнением.
Замечание: характеристическое уравнение можно
получать, делая следующие замены y k 2, y k , y k 0 1.
В зависимости от корней этого уравнения, общее решение
находится тремя способами.

4.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
1. Если дискриминант характеристического уравнения
больше нуля, то есть D b 2 4ac 0 , то уравнение имеет
два различных вещественных корня
b D .
b D и
k1
k2
2a
2a
Тогда
общее
решение
исходного
однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами имеет вид
yoo C1 e k1 x C2 e k 2 x .

5.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
2. Если дискриминант характеристического уравнения
равен нулю, то есть D b 2 4ac 0 , то уравнение имеет
два одинаковых вещественных корня
b
k1 k 2 .
2a
Тогда
общее
решение
исходного
однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами имеет вид
yoo e k1 x C1 C2 x .

6.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
3. Если дискриминант характеристического уравнения
D b 2 4ac 0 , то уравнение
меньше нуля, то есть
имеет два сопряжённых комплексных корня.
Пусть D 1 d 2 1 d 2 d 1 d i, где d>0, i 1 .
Тогда корни характеристического уравнения будут равны
k1, 2
b D b d i
b
d
i i.
2a
2a
2a 2a
Тогда
общее
решение
исходного
однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами имеет вид
yoo e x C1 cos x C2 sin x .

7.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 1
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами 2 y 5 y 3 y 0 .
Решение.
Используем замены y k 2, y k , y 1 .
Получим характеристическое уравнение 2k 2 5k 3 0 .
Дискриминант квадратного уравнения
D 25 4 2 3 25 24 49 0, следовательно, выберем
формулу из случая 1.
Корни характеристического уравнения равны
k1
5 7
5 7
0,5, k 2
3,
4
4
тогда общее решение исходного дифференциального
0,5 x
C2 e3 x.
уравнения имеет вид yоо C1 e
0,5 x
3x
y
C
e
C
e
.
Ответ: оо
1
2

8.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 2
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 2 y y 0 .
Решение.
Используем замены y k 2, y k , y 1 .
Получим характеристическое уравнение k 2 2k 1 0 .
Дискриминант квадратного уравнения D 4 4 1 1 0 ,
следовательно, выберем формулу из случая 2.
2
Корни характеристического уравнения равны k1 k2 1,
2
то есть квадратный трёхчлен является полным квадратом
k 1 2 0 .
Тогда общее решение исходного дифференциального
x
уравнения имеет вид yoo e C1 C2 x .
x
Ответ: yoo e C1 C2 x .

9.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 3
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 2 y 5 y 0 .
Решение.
Используем замены y k 2, y k , y 1 .
Получим характеристическое уравнение k 2 2k 5 0 .
Дискриминант квадратного уравнения
D 4 4 1 5 4 20 16 0 ,
следовательно,
выберем
формулу из случая 3.
тогда
корни
D 16 16 1 16 1 4i,
характеристического уравнения k1,2 2 4i 2 1 2i 1 2i .
2
2
Здесь α=1, β=2, значит общее решение исходного
дифференциального уравнения имеет вид
yоо e x C1 cos 2 x C2 sin 2 x .
Ответ: yоо e x C1 cos 2 x C2 sin 2 x .

10.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 4
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 9 y 0.
Решение.
Используем замены y k 2, y k.
Получим характеристическое уравнение
k 2 9k 0 или
k k 9 0 .
Решения уравнения k1=0, k2=–9 – различные вещественные
корни, следовательно, выберем формулу из случая 1.
Тогда общее решение исходного дифференциального
уравнения имеет вид yоо C1 e0 x C2 e 9 x C1 C2 e 9 x .
Ответ: yоо C1 C2 e 9 x .

11.

4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 5
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 9 y 0 .
Решение.
Используем замены y k 2, y 1 .
Получим характеристическое уравнение k 2 9 0 , откуда
выразим k 2 9 или
k1, 2 9 1 9 1 9 i 3 0 3i ,
то есть мы
получили пару сопряжённых комплексных корней,
следовательно, выберем формулу из случая 3.
Здесь α=0, β=3, значит общее решение исходного
дифференциального уравнения имеет вид
yоо e 0 x C1 cos 3x C2 sin 3x C1 cos 3x C2 sin 3x .
Ответ:
yоо C1 cos 3x C2 sin 3x .

12.

П
4.3.1 Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 6
Найти общее решение однородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 5 y 0 .
Решение.
Используем замены y k 2, y 1.
Получим характеристическое уравнение
k2 5 .
или
k2 5 0
k2 5
Решения уравнения k1 5 ,
– различные
вещественные корни, следовательно, выберем формулу из
случая 1.
Тогда общее решение исходного дифференциального
уравнения имеет вид yоо C1 e 5 x C2 e 5 x .
Ответ: yоо C1 e
5 x
C2 e
5 x
.

13.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Дифференциальное уравнение вида
a y b y c y f x ,
где a, b, c – числа (причём а≠0), и называется линейным
неоднородным
дифференциальным
уравнением
второго порядка с постоянными коэффициентами.
Структура общего решения линейного неоднородного
дифференциального уравнения второго порядка с
постоянными коэффициентами имеет вид
y yoo yчн ,
где yoo – решение соответствующего однородного
дифференциального уравнения, yчн – частное решение,
которое выбирается в зависимости от вида функции .

14.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Выбор частного решения yчн
Если f(x) = d, где d = const, d ≠ 0 то yчн A x.r
Степень r выбирается следующим образом:
– если среди корней характеристического уравнения нет
корня k = 0, то r = 0;
– если одним из корней характеристического уравнения
является k = 0, то r = 1.
Число А находится путём подстановки полученного yчн в
условие.

15.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 7
Найти общее решение неоднородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 8 y 16.
Решение.
Решим соответствующее однородное дифференциальное
уравнение y 8 y 0 . Используем замены y k 2, y k .
Получим характеристическое уравнение
k k 8 0 .
k 2 8k 0
или
Решения уравнения k1=0, k2=8 – различные вещественные
корни, следовательно, выберем формулу из случая 1.
Тогда общее решение однородного дифференциального
уравнения имеет вид yоо C1 e0 x C2 e8 x C1 C2 e8 x .

16.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Теперь определим вид частного решения yчн в зависимости
от функции, стоящей в правой части уравнения. Так как
r
f(x) = 16, то
, где r = 1,yпоскольку
одним из
чн A x
корней характеристического уравнения является k = 0.
Так как
, то
и
.
A 0
и
yчн
yчн
A x A в уравнение
yчнзначения
A x
Подставим
y 0
и найдём значение А: y A
y 8 y 16
0 8 A 16,
A 2,
yчн дифференциального
2x.
Общее решение искомого
уравнения
примет вид
y yoo yчн С1 C2 e8 x 2 x.
Ответ:
y С1 C2 e8 x 2 x.

17.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Пример 8
Найти общее решение неоднородного
дифференциального уравнения второго порядка с
постоянными коэффициентами y 8 y 7 y 14.
Решение.
Решим соответствующее однородное дифференциальное
уравнение y 8 y 7 y 0 .
Используем замены y k 2, y k, y 1.
Получим характеристическое уравнение k 2 8k 7 0 .
Дискриминант равен D 64 4 1 7 64 28 36 0, тогда
решения уравнения k1 8 6 1, k2 8 6 7 – различные
2
6
вещественные корни, следовательно, выберем формулу из
случая 1.
Тогда общее решение однородного дифференциального
уравнения имеет вид yоо C1 e x C2 e7 x .

18.

4.3.2 Линейные неоднородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Теперь определим вид частного решения yчн в зависимости
от функции, стоящей в правой части уравнения. Так как
f(x) = 14, то
, где r = 0, поскольку среди корней
характеристического уравнения нет корня k = 0.
Так как
, то
и
.
0
уравнение
0 0
A и
yчн значения
A x0 A
Подставим
, yчн
вyчн
y значение
A y 0 А: y 0
и найдём
y 8 y 7 y 14
0 8 0 7 A 14,
A 2,
yчндифференциального
2.
Общее решение искомого
уравнения
примет вид
y yoo yчн С1 e x C2 e7 x 2.
Ответ:
y С1 e x C2 e7 x 2.

19.

4.4 Приложения дифференциальных уравнений
в экономике
Исследование природных процессов и изучение
закономерностей общественных процессов приводят к
построению математических моделей, основой которых
являются дифференциальные уравнения.
Пример 9 Из статистических данных известно, что для
рассматриваемого региона число новорожденных и число
умерших за единицу времени пропорциональны
численности
населения
с
коэффициентами
пропорциональности соответственно k1 и k2. Найти закон
изменения численности населения с течением времени
(описать протекание демографического процесса).

20.

4.4 Приложения дифференциальных уравнений
в экономике
Решение.
Пусть y=y(t) – число жителей региона в момент времени t.
Прирост населения Δy за время Δt равен разности между
числом родившихся и умерших за это время, то есть
y k1 y t k2 y t ,
y
k1 k 2 y,
t
y
k y, где k k1 k2 .
t
Тогда lim y k y или
y k y , то есть математическая
t 0 t
модель демографического процесса представляет собой
дифференциальное
уравнение
с
переменными. Решим это уравнение.
разделяющимися

21.

4.4 Приложения дифференциальных уравнений
в экономике
y k y,
dy
k y,
dt
dy
k dt ,
y
dy
y k dt,
ln y k t C ,
y e k t C ,
y C1 e k t, где C1 eC.
Таким образом, закон изменения численности населения с
y C1 e k t , где C1 –
течением времени примет вид
постоянная,
определяемая
начальными
условиями
(численностью населения в начальный момент времени).
Ответ: y C1 e k t .

22.

4.4 Приложения дифференциальных уравнений
в экономике
Пример 10 Функции спроса D=D(t) и предложения S=S(t)
от цены товара P, где t – время, имеют следующие
аналитические выражения:
D 4P P P 37 и S 5P 3P 4P 7.
Найти уравнение, выражающее зависимость цены P=P(t)
от времени t при равновесном состоянии рынка.
Решение.
Для определения равновесной цены следует решить
уравнение 4P P P 37 5P 3P 4P 7 , которое после
упрощения примет вид: P 4P 5P 30 .
Данное дифференциальное уравнение относится к классу
неоднородных дифференциальных уравнений второго
порядка с постоянными коэффициентами.

23.

4.4 Приложения дифференциальных уравнений
в экономике
Характеристическое
уравнение k 2 4k 5 0 имеет
комплексные корни k1,2 2 i
и общее решение
соответствующего
однородного
дифференциального
уравнения имеет вид: Pоо e 2t C1 cos t C2 sin t .
Частное решение неоднородного дифференциального
уравнения имеет вид: Pчн А , тогда Pчн Pчн 0 .
Подставляя эти значения в начальное уравнение, получаем
5 Pчн 30 Pчн 6.
Общее решение неоднородного
уравнения
второго
порядка
коэффициентами примет вид:
дифференциального
с
постоянными
P t Pоо Pчн e 2t C1 cos t C2 sin t 6.
Ответ:
P t e 2t C1 cos t C2 sin t 6.