Similar presentations:
Математические аспекты двухмерной машинной графики
1. МАТЕМАТИЧЕСКИЕ АСПЕКТЫ ДВУХМЕРНОЙ МАШИННОЙ ГРАФИКИ
12.
Основной задачей машинной графики являетсявоспроизведение изображений на экране, исходя из их
математических описаний.
Для этого необходимо создание графического файла, т.
е. выполнение основных операций машинной графики:
преобразование координат, преобразования на плоскости,
определение расстояний, периметров, геометрические
преобразования (пересечения объектов), установление
видимости (отсечение и покрытие).
Вычисления на плоскости не представляют труда и
основаны на понятиях планиметрии и аналитической
геометрии.
2
3.
Очевидно, невозможно отделить компьютернуюграфику от координатной геометрии,
Существенным моментом здесь является полное
понимание вопросов, связанных с двухмерным и
трехмерным представлением объектов в теории
Евклидовой и Декартовой координатной геометрии, и
тригонометрии,
а также хорошее знание эффективных приемов
программирования (манипуляции с кодированием и
хранением данных), чтобы справиться с создания
больших и сложных графических изображений.
3
4. 2D геометрия Скаляр, Вектор, Матрица
• Скаляр• (пропись, italic)
• Вектор
a
a a1
a2 ... an
• (пропись, bold)
• Матрица
• (заглавн., bold)
a11 a12
A a21 a22
a31 a32
a13
a23
a33
4
5. Вектора
• Стрелка: длина и направление• ориентированный сегмент в nD
пространстве
• Смещение
• местоположение,
если задан центр
5
6.
• Вектор определяется направлением и…?величиной (также называют норма или длина),
• Вектор м.б. использован для представления чего?
направления, силы…
• Что такое единичный вектор?
вектор величиной 1 (измеряется в выбранных
единицах)
• Что представляет единичный вектор?
направление (tang, внешняя нормаль)
• Что есть sV, где s это скаляр?
вектор с направлением V, но норма масштабирована
на s
• Что есть U+V?
сумма смещений U и V
6
7. 2D геометрия Скаляр, Вектор, Матрица
• Точки, векторы,определенные
относительно
системы координат
• Точка: расположение
в системе координат
• Пример: Точка (5,4)
7
8. Описание векторов
• Вектор-строка a row a1a2 ... an
a1
• Вектор-столбец
a
2
a col
...
an
• Переход с транспонированной формой
a
T
col
a row
8
9. Сложение вектор-вектор
• Сложить: vector + vector = vector• Правило параллелограмма
• “хвост к голове” закончит треугольник
геометрически
u v
v
u
Примеры:
алгебраически
u1 v1
u v u 2 v2
u3 v3
(3,2) (6,4) (9,6)
(2,5,1) (3,1, 1) (5,6,0)
9
10. Вычитание вектор-вектор
• вычитание: vector - vector = vectorv
u
v
u v u ( v)
Примеры:
u1 v1
u v u 2 v2
u3 v3
(3,2) (6,4) ( 3, 2)
(2,5,1) (3,1, 1) ( 1,4,2)
10
11. Умножение Скаляр-вектор
• умножение: scalar * vector = vector• Вектор масштабируется
a *u
a * u (a * u1 , a * u2 , a * u3 )
u
Примеры:
2 * (3,2) (6,4)
.5 * (2,5,1) (1,2.5,.5)
11
12. Умножение вектор-вектор
• умножение: vector * vector = scalar• скалярное произведение
(dot product)
u v
u1 v1
u v u v u v u v
1
1
2
2
3
3
2 2
u3 v3
12
13. Умножение вектор-вектор (Свойства)
• Симметрия (или коммутативность):• Линейность:
• Однородность:
a b b a
(a c) b a b c b
( sa ) b s(a b)
13
14. Умножение вектор-вектор (2)
• умножение : vector * vector = scalar• скалярное произведение
u v
u1 v1
u v u v u v u v
1
1
2
2
3
3
2 2
u3 v3
14
15. Умножение вектор-вектор (3)
• умножение : vector * vector = scalar• скалярное произведение
u v
u1 v1
u v u v u v u v
1
1
1
2
3
3
2 2
u3 v3
• Геометрическая интерпретация
• длины, углы
• можно найти угол между
двумя векторами
u v u v cos
u
v
15
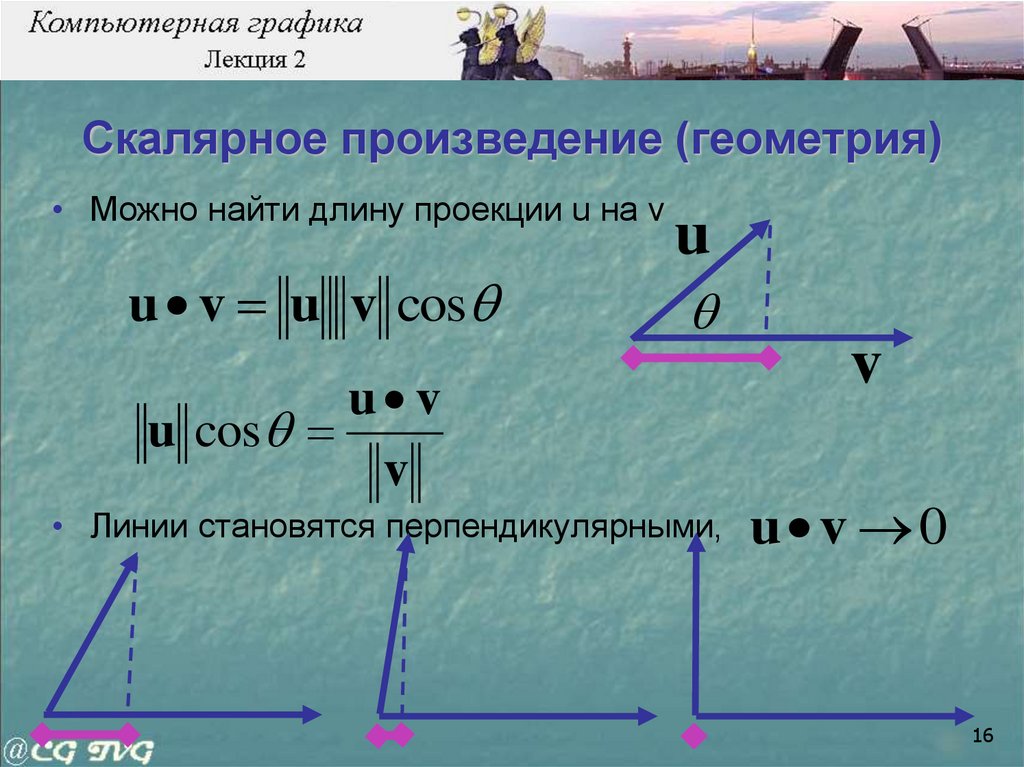
16. Скалярное произведение (геометрия)
• Можно найти длину проекции u на vu v u v cos
u
u v
u cos
v
• Линии становятся перпендикулярными,
v
u v 0
16
17. Скалярное произведение (геометрия)
• Углы между векторамиb c
17
18. Скалярное произведение (2)
U V = ||U|| ||V|| cos(angle(U,V)) U V - скаляр.U and V ортогональны U V==0
U V==0 ( U==0 или V==0 или (U и V ортогональны)
U V положительно если угол между U и V меньше 90o
U V = V U, потому, что: cos(a)=cos(–a).
u v = cos(angle(u,v)
# unit vectors: ||u|| = ||v|| = 1
Скалярное произведение двух единичных векторов - косинус их угла
V u = длина проекции V в направлении (единич.вектор) u
||U||= √(U U) = длина U = норма U
U2 = U U (короткая форма для ||U||2)
v
cos(angle(u,v))
u
V U = U V > 0
V U = U V < 0
18
19. Скалярное произведение(пример)
u1 v1u v u v u v u v
1
1
1
2
3
3
2 2
u3 v3
6 1
1 7 (6 *1) (1* 7) ( 2 * 3) 6 7 6 19
2 3
19
20.
• Что измеряет скалярное произведение V U когда Uединич.вектор?
Спроектированное смещение V на U
• Чему равно V U когда U и V единич.вектора?
cos( angle(U,V) )
• Чему равно V U для обычных U и V?
cos( angle(U,V) ) V.norm U.norm
• Когда V U=0?
U.norm=0 OR V.norm=0 OR U и V ортогональны
• Когда V U>0?
если угол между U и V меньше 90o
• Как подсчитать V U?
U.xV.x+U.yV.y
• Что такое V2?
V2 = V V = (V.norm)2
20
21.
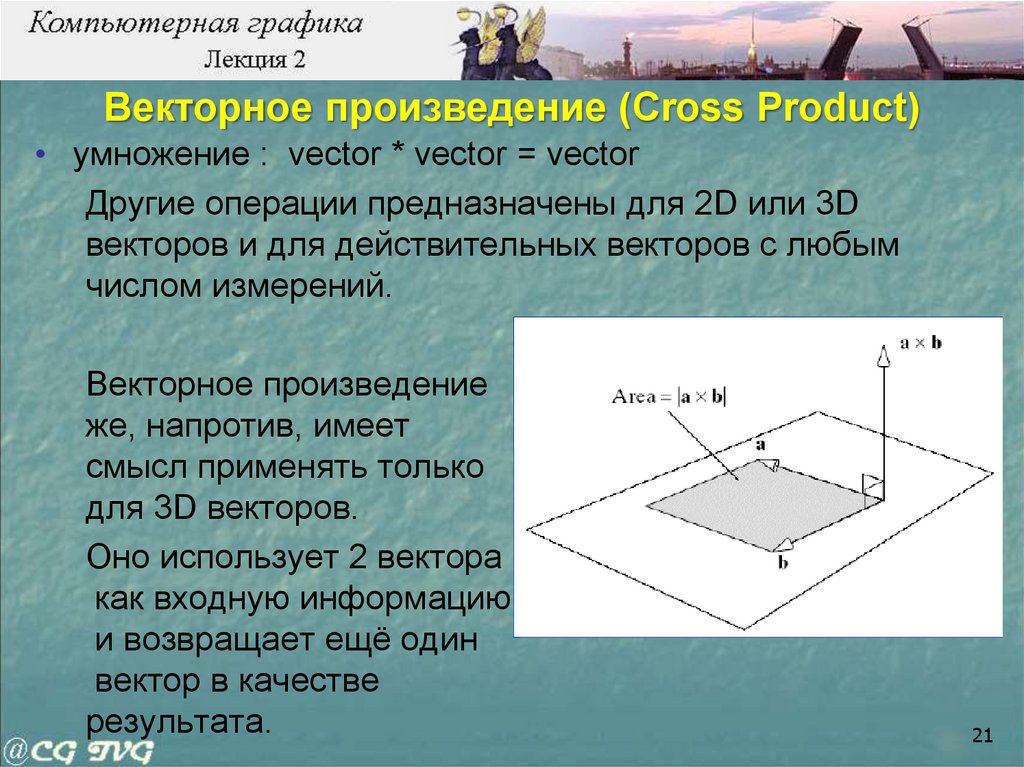
Векторное произведение (Cross Product)• умножение : vector * vector = vector
Другие операции предназначены для 2D или 3D
векторов и для действительных векторов с любым
числом измерений.
Векторное произведение
же, напротив, имеет
смысл применять только
для 3D векторов.
Оно использует 2 вектора
как входную информацию
и возвращает ещё один
вектор в качестве
результата.
21
22.
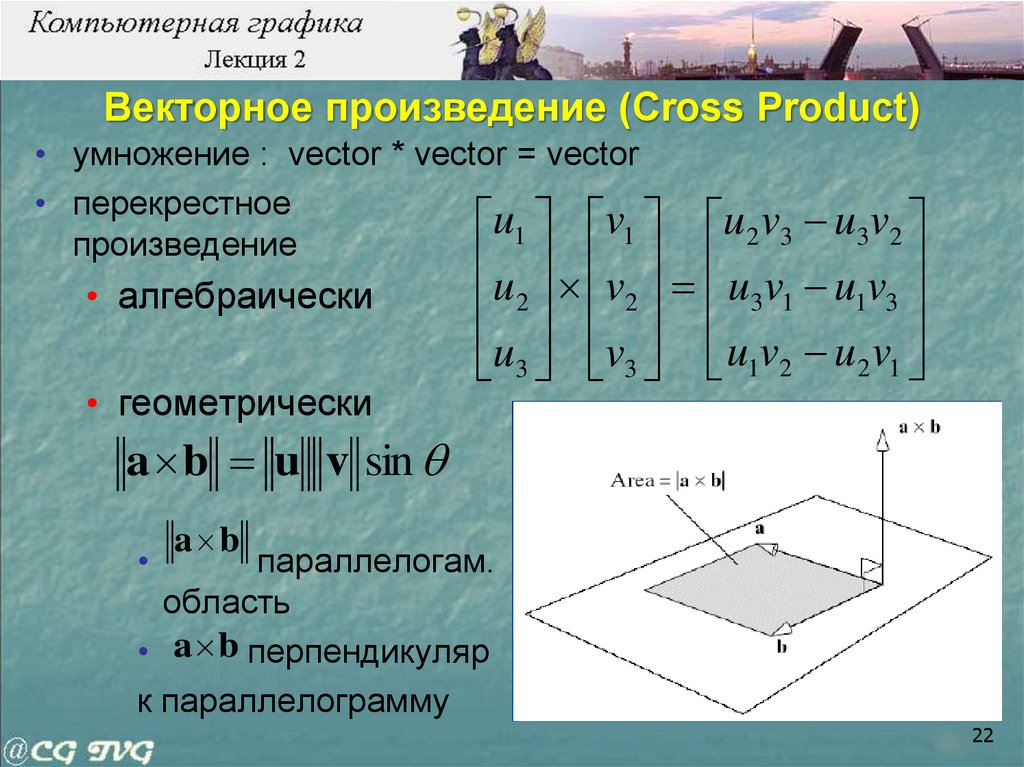
Векторное произведение (Cross Product)• умножение : vector * vector = vector
• перекрестное
u1 v1
произведение
• алгебраически
• геометрически
u 2 v3 u3v2
u v u v u v
2 2 3 1 1 3
u3 v3 u1v2 u2 v1
a b u v sin
a b
параллелогам.
область
• a b перпендикуляр
к параллелограмму
22
23.
Векторное произведение (Cross Product)• умножение: vector * vector = vector
• перекрестное произведение
• алгебраически
u1 v1 u 2 v3 u3v2
u v u v u v
2 2 3 1 1 3
u3 v3 u1v2 u2 v1
23
24.
• Правосторонняя и Левосторонняякоординатные системы
В трехмерной (3d) графике используют две системы
координат: правосторонняя и левосторонняя.
В обоих этих системах Х и Y положительны, т.е. Х смотрит
вправо, Y - вверх.
Вы можете запомнить положительное направление оси Z
направляя палец левой или правой Вашей руки. Направьте Ваш
большой палец от себя, это направление является положительным
по оси Z.
24
25. Понятие базиса системы векторов
• Ба́зис (др.-греч. βάσις «основа») —упорядоченный (конечный или
бесконечный) набор векторов в векторном
пространстве, такой, что любой вектор
этого пространства может быть
единственным образом представлен в
виде линейной комбинации векторов из
этого набора. Векторы базиса
называются базисными векторами.
25
26. Базис на плоскости и в трёхмерном пространстве
Любой декартовой системе координат на плоскостиили в трёхмерном пространстве (также и в
пространстве другой размерности) может быть
сопоставлен базис, состоящий из векторов, каждый из
которых направлен вдоль своей координатной оси.
Это относится и к прямоугольным декартовым
координатам (тогда соответствующий базис
называется ортогональным), так и к косоугольным
декартовым координатам (которым будет
соответствовать не ортогональный базис).
26
27. Базис на плоскости и в трёхмерном пространстве
Часто удобно выбрать длину (норму) каждого избазисных векторов единичной, такой базис называется
нормированным.
Наиболее часто базис выбирают ортогональным и
нормированным одновременно, тогда он
называется ортонормированным.
В любом векторном пространстве базис можно
выбрать различным образом (поменяв направления
его векторов или их длины, например).
27
28. Ортонормальный базисный вектор
• Если базисные вектора ортонормальные( ортонормальные( перпендикулярные) и единичной
длины)
• Мы имеем Картезианскую (Декартову) систему
координат
• знакомое Пифагорово
определение расстояния
Ортонормальные алгебраические
свойства
x y 1,
x y 0
28
29. Стандартные единичные векторы в 3D
i = (1,0,0)j = (0,1,0)
k = (0,0,1)
Правая рука
Левая рука
29
30. Стандартные единичные векторы в 3D
Векторное пространствоназывается n-мерным, если в нем можно
найти n линейно независимых векторов, но больше, чем n линейно независимых
векторов оно не содержит.
Размерность пространства – это максимальное число содержащихся в нем
линейно независимых векторов.
Размерность пространства
условимся обозначать через dim.
Например, размерность множества всех плоских векторов равна 2, размерность
множества пространственных векторов равна 3.
Пространство, имеющее конечную размерность, называется конечномерным.
Пространство, в котором можно найти сколь угодно много линейно независимых
векторов, называется бесконечномерным.
Совокупность n линейно независимых векторов n- мерного векторного
пространства
называется его базисом.
30
31. Линии
• форма наклонной, сточками пересечения
• y = mx + b
• неявная форма
• y – mx – b = 0
• Ax + By + C = 0
• f(x,y) = 0
31
32. Окружность
f ( x, y ) ( x xc ) ( y yc ) r
2
2
2
• окружность – это точки (x,y), где f(x,y) = 0
p ( x, y ), c ( xc , yc ) : (p c) (p c) r 2 0
• точки p на окружности имеют свойство, что
вектор из c в p дает скалярное произведение r2
p c r 0
2
2
• точки p на окружности имеют свойство, что
квадрат расстояния из c в p - r2
p c r 0
• точки p на окружности – расстоние r из центра c
32
33. Параметрические кривые
• Параметр: индекс изменяющийсянепрерывно
• (x,y): точка на кривой
• t: параметр
x g (t )
y h(t )
• Вектор из
p f (t )
33
34. 2D параметрическая линия
d2D параметрическая линия
x x 0 t(x1 x 0 )
•
y y 0 t(y1 y 0 )
• p(t ) p 0 t (p1 p 0 )
• p(t ) o t (d)
• Начинается в точке p0,
и идет до p1,
в соответствии с параметром t
• p(0) = p0, p(1) = p1
• Линия: множество всех точек,
проходящих через P0 в
направлении вектора d
34
35. Матрицы
• Множество чисел (m×n = m строки, n столбцы)1 3
5
2
0 4
• Сложение, умножение скаляром просто : элемент
за элементом
35
36. Сложение матриц
• сложение: matrix + matrix = matrixm11 m12 n11 n12 n11 m11 n12 m12
m
21 m22 n21 n22 n21 m21 n22 m22
• пример
1 3 2 5 1 ( 2) 3 5 1 8
2 4 7 1 2 7
4 1 9 5
36
37. Умножение скаляр - матрица
• умножение: скаляр * matrix = matrixm11 m12 a * m11 a * m12
a
m21 m22 a * m21 a * m22
• пример
2 4 3 * 2 3 * 4 6 12
3
1 5 3 *1 3 * 5 3 15
37
38. Умножение матрица-матрица
• Можно только умножить (n,k) на (k,m):число левых столбцов = числу правых строк
• разрешено
h i
a b c
e f g j k
l
m
• неопределено
a b c
e f g h i
j k
o p q
38
39.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
39
40.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
40
41.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
41
42.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
p22 m21n12 m22n22
42
43.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
p22 m21n12 m22n22
• некоммутативно: AB != BA
p12
p22
43
44.
Умножение матрица-вектор• точки вектора-столбца: постумножаются
x' m11 m12
y '
m21 m22
z ' m31 m32
h' m41 m42
m13
m23
m33
m43
m14 x
m24 y
m34 z
m44 h
p' Mp
• точки вектора-строка : предумножаются
x'
y ' z ' h' x
y
m11 m12
m21 m22
z h
m31 m32
m41 m42
m13
m23
m33
m43
m14
m24
m34
m44
T
p' p M
T
T
T
44
45.
Умножение матрица-матрицаПример умножения матриц
1 3
9 27 33 13
3 6 9 4
5
2
19
44
61
26
2 7 8 3
0 4
8
28
3
2
1
2
45
46.
Матрицы• транспонированная
m
m
m
11
12
m21 m22
m31 m32
m41 m42
идентичности
1
0
0
0
• обратная
13
m23
m33
m43
0 0
1 0
0 1
0 0
m14
m24
m34
m44
0
0
0
1
T
m11
m
12
m13
m14
m21
m31
m22
m32
m23
m33
m24
m34
m41
m42
m43
m44
AA 1 I
• не все матрицы являются обратимыми
46
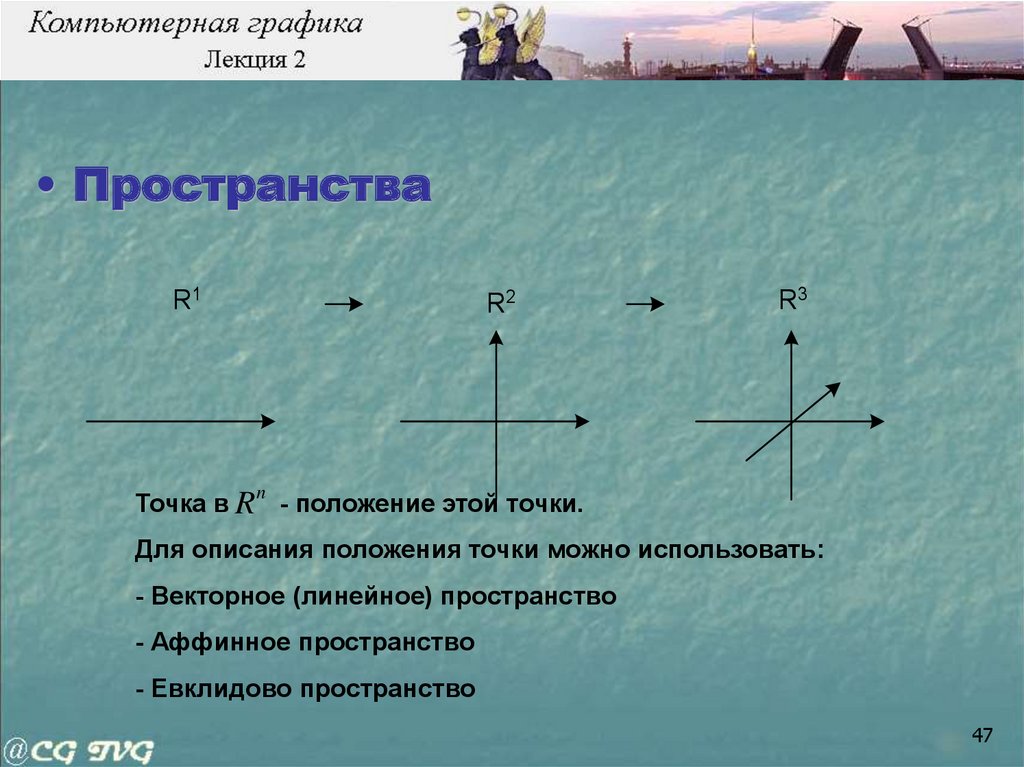
47.
• ПространстваR1
R2
R3
n
Точка в R - положение этой точки.
Для описания положения точки можно использовать:
- Векторное (линейное) пространство
- Аффинное пространство
- Евклидово пространство
47
48.
• Линейное пространство создают скаляры ивекторы.
• Аффинное пространство – добавляется понятие точки.
• Евклидово пространство – вводят понятие
расстояние.
• Системы координат: Положение точки в пространстве
может быть описано в виде комбинации некоторых
линейно-независимых векторов .
• Если ввести скаляры , то можно описать вектор
(положение точки) так:
W 1V1 2V2 3V3
48
49.
Декартова (Картезианская) система координатКриволинейная система координат
(1)
Декартова прямоугольная система
координат (2)
Декартова прям. сист.
координат на плоскости
(3)
Декарт. прям. сист. корд. в
3-мерном пространстве (5)
Правосторонняя
система координат (8)
Полярные координаты (4)
Цилиндрическая система
координат (6)
Сферическая система
координат (7)
Левосторонняя система
координат (9)
49
50.
• Базовая косоугольная система координатКоординаты определяются осями ( х – ось абсцисс,
у - ось ординат)
Расстояние определяется проекциями P ( x, y )
• Полярная система координат
Точка О – полюс, - полярный угол , r – полярное
расстояние.
50
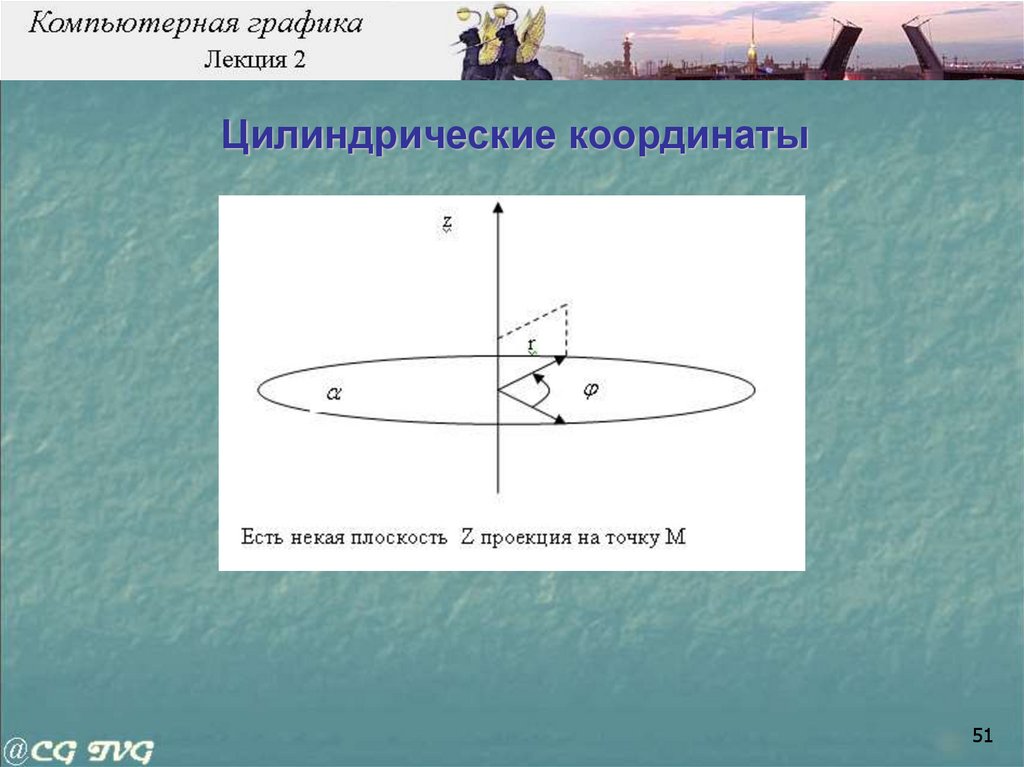
51.
Цилиндрические координаты51
















































 mathematics
mathematics








