Similar presentations:
Скаляр, вектор, матрица. 2D геометрия
1. 2D геометрия Скаляр, Вектор, Матрица
• Скаляр• (пропись, italic)
• Вектор
a
a a1
a2 ... an
• (пропись, bold)
• Матрица
• (заглавн., bold)
a11 a12
A a21 a22
a31 a32
a13
a23
a33
1
2. Вектора
• Стрелка: длина и направление• ориентированный сегмент в nD
пространстве
• Смещение
• местоположение,
если задан центр
2
3.
• Вектор определяется направлением и…?величиной (также называют норма или длина),
• Вектор м.б. использован для представления чего?
направления, силы…
• Что такое единичный вектор?
вектор величиной 1 (измеряется в выбранных
единицах)
• Что представляет единичный вектор?
направление (tang, внешняя нормаль)
• Что есть sV, где s это скаляр?
вектор с направлением V, но норма масштабирована
на s
• Что есть U+V?
сумма смещений U и V
3
4. Описание векторов
• Вектор-строка a row a1a2 ... an
a1
• Вектор-столбец
a
2
a col
...
an
• Переход с транспонированной формой
a
T
col
a row
4
5. Сложение вектор-вектор
• Сложить: vector + vector = vector• Правило параллелограмма
• “хвост к голове” закончит треугольник
геометрически
u v
v
u
Примеры:
алгебраически
u1 v1
u v u 2 v2
u3 v3
(3,2) (6,4) (9,6)
(2,5,1) (3,1, 1) (5,6,0)
5
6. Вычитание вектор-вектор
• вычитание: vector - vector = vectorv
u
v
u v u ( v)
Примеры:
u1 v1
u v u 2 v2
u3 v3
(3,2) (6,4) ( 3, 2)
(2,5,1) (3,1, 1) ( 1,4,2)
6
7. Умножение Скаляр-вектор
• умножение: scalar * vector = vector• Вектор масштабируется
a *u
a * u (a * u1 , a * u2 , a * u3 )
u
Примеры:
2 * (3,2) (6,4)
.5 * (2,5,1) (1,2.5,.5)
7
8. Умножение вектор-вектор
• умножение: vector * vector = scalar• скалярное произведение
u v
u1 v1
u v u v u v u v
1
1
2
2
3
3
2 2
u3 v3
8
9. Умножение вектор-вектор (2)
• умножение : vector * vector = scalar• скалярное произведение
u v
u1 v1
u v u v u v u v
1
1
2
2
3
3
2 2
u3 v3
9
10. Умножение вектор-вектор (3)
• умножение : vector * vector = scalar• скалярное произведение
u v
u1 v1
u v u v u v u v
1
1
1
2
3
3
2 2
u3 v3
• Геометрическая интерпретация
• длины, углы
• можно найти угол между
двумя векторами
u v u v cos
u
v
10
11. Скалярное произведение (геометрия)
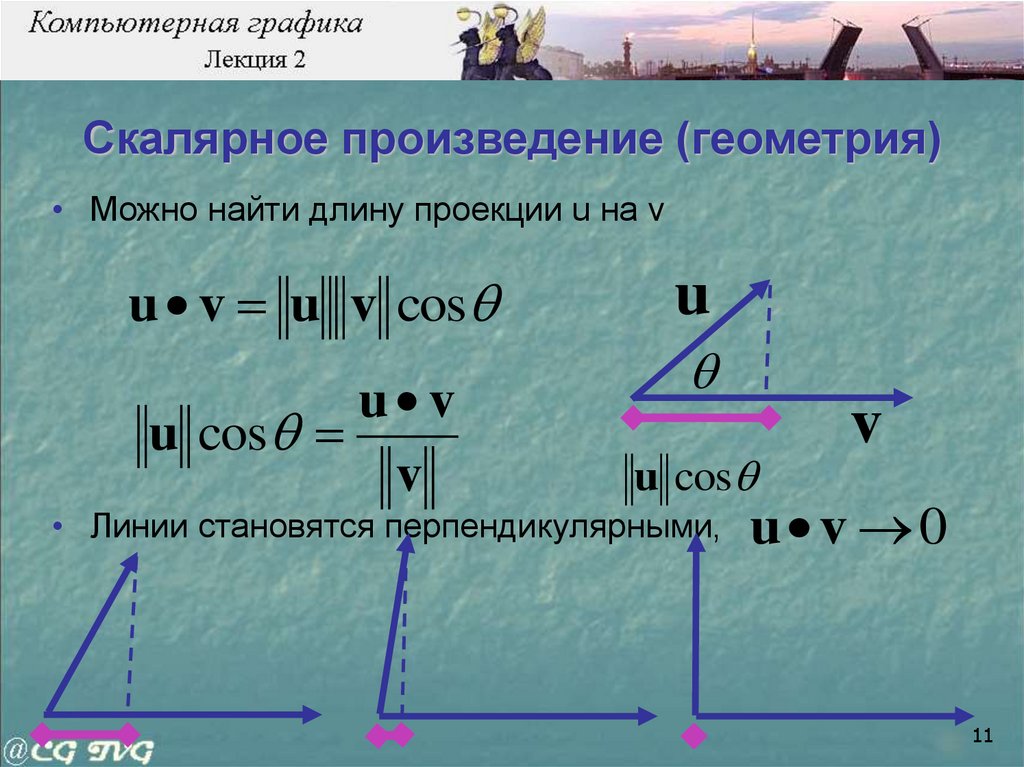
• Можно найти длину проекции u на vu v u v cos
u v
u cos
v
u
u cos
• Линии становятся перпендикулярными,
v
u v 0
11
12. Скалярное произведение (2)
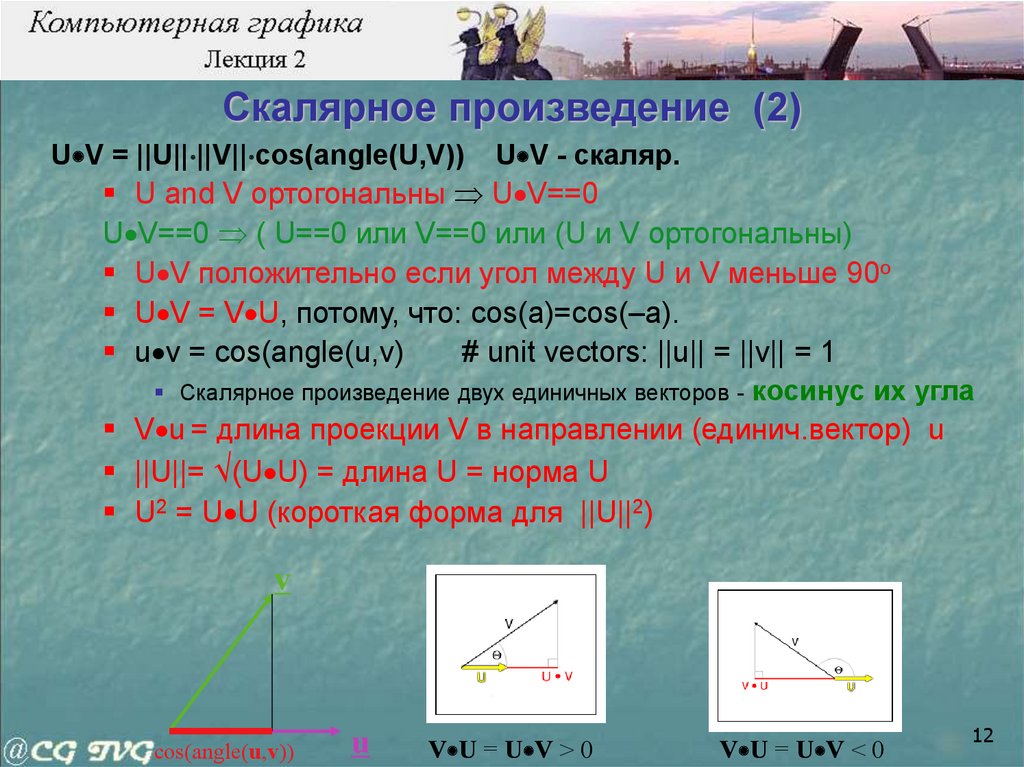
U V = ||U|| ||V|| cos(angle(U,V)) U V - скаляр.U and V ортогональны U V==0
U V==0 ( U==0 или V==0 или (U и V ортогональны)
U V положительно если угол между U и V меньше 90o
U V = V U, потому, что: cos(a)=cos(–a).
u v = cos(angle(u,v)
# unit vectors: ||u|| = ||v|| = 1
Скалярное произведение двух единичных векторов - косинус их угла
V u = длина проекции V в направлении (единич.вектор) u
||U||= √(U U) = длина U = норма U
U2 = U U (короткая форма для ||U||2)
v
cos(angle(u,v))
u
V U = U V > 0
V U = U V < 0
12
13. Скалярное произведение(пример)
u1 v1u v u v u v u v
1
1
1
2
3
3
2 2
u3 v3
6 1
1 7 (6 *1) (1* 7) ( 2 * 3) 6 7 6 19
2 3
13
14.
• Что измеряет скалярное произведение V U когда Uединич.вектор?
Спроектированное смещение V на U
• Чему равно V U когда U и V единич.вектора?
cos( angle(U,V) )
• Чему равно V U для обычных U и V?
cos( angle(U,V) ) V.norm U.norm
• Когда V U=0?
U.norm=0 OR V.norm=0 OR U и V ортогональны
• Когда V U>0?
если угол между U и V меньше 90o
• Как подсчитать V U?
U.xV.x+U.yV.y
• Что такое V2?
V2 = V V = (V.norm)2
14
15.
Скалярное произведение(Продолжение)• умножение: vector * vector = vector
• перекрестное произведение
• алгебраически
u1 v1 u 2 v3 u3v2
u v u v u v
2 2 3 1 1 3
u3 v3 u1v2 u2 v1
15
16.
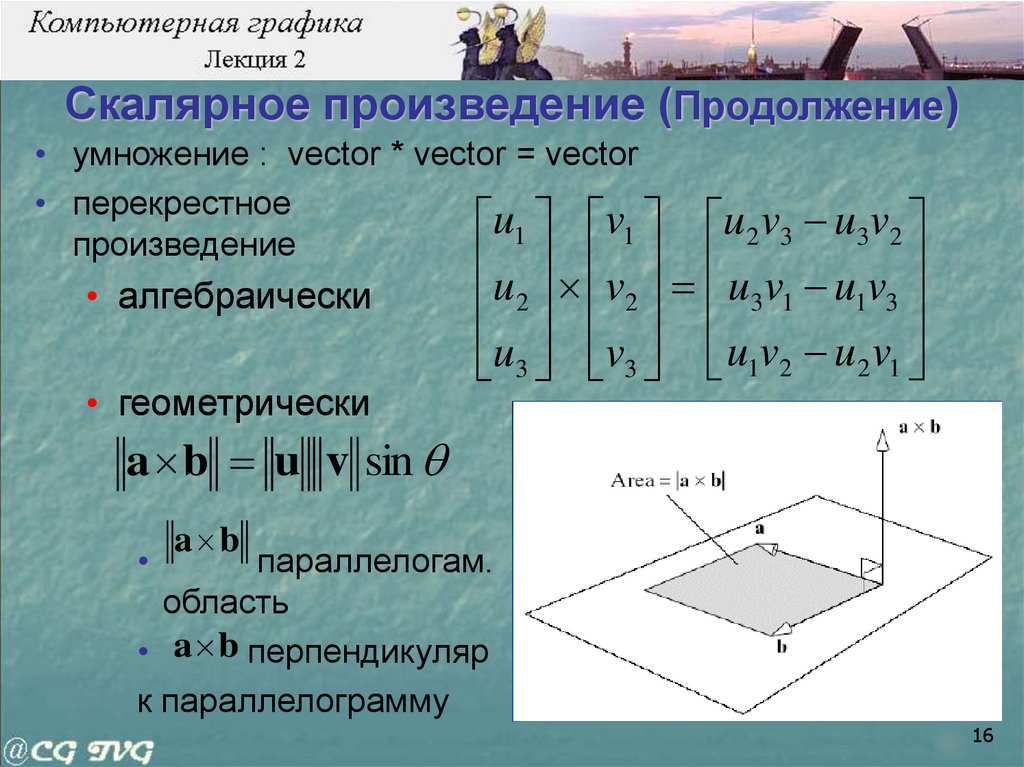
Скалярное произведение (Продолжение)• умножение : vector * vector = vector
• перекрестное
u1 v1
произведение
• алгебраически
• геометрически
u 2 v3 u3v2
u v u v u v
2 2 3 1 1 3
u3 v3 u1v2 u2 v1
a b u v sin
a b
параллелогам.
область
• a b перпендикуляр
к параллелограмму
16
17.
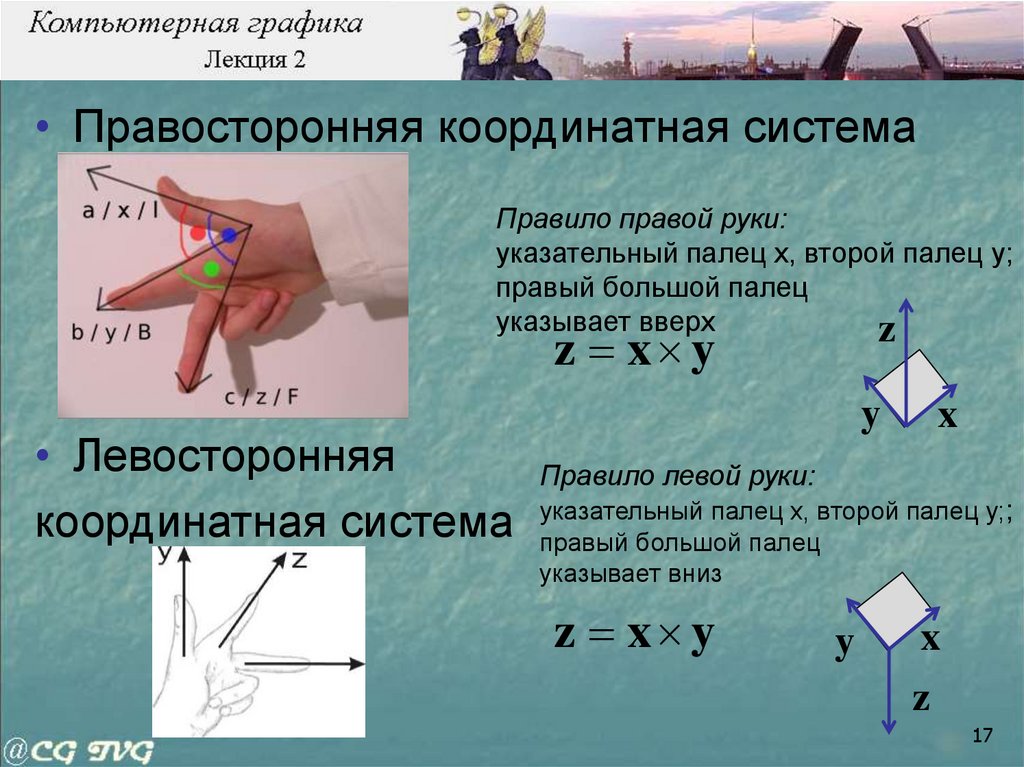
• Правосторонняя координатная системаПравило правой руки:
указательный палец x, второй палец y;
правый большой палец
указывает вверх
z
z x y
• Левосторонняя
координатная система
y
x
Правило левой руки:
указательный палец x, второй палец y;;
правый большой палец
указывает вниз
z x y
y
x
z
17
18. Векторы базиса
• Взять любых два линейно-независимых вектора(не равных 0 и не ||)
• Можно использовать их линейную комбинацию
для определения
любого другого
вектора :
c w1a w2b
18
19. Ортонормальный базисный вектор
• Если базисные вектора ортонормальные( ортонормальные( перпендикулярные) и единичной
длины)
• Мы имеем Картезианскую (Декартову) систему
координат
• знакомое Пифагорово
определение расстояния
Ортонормальные алгебраические
свойства
x y 1,
x y 0
19
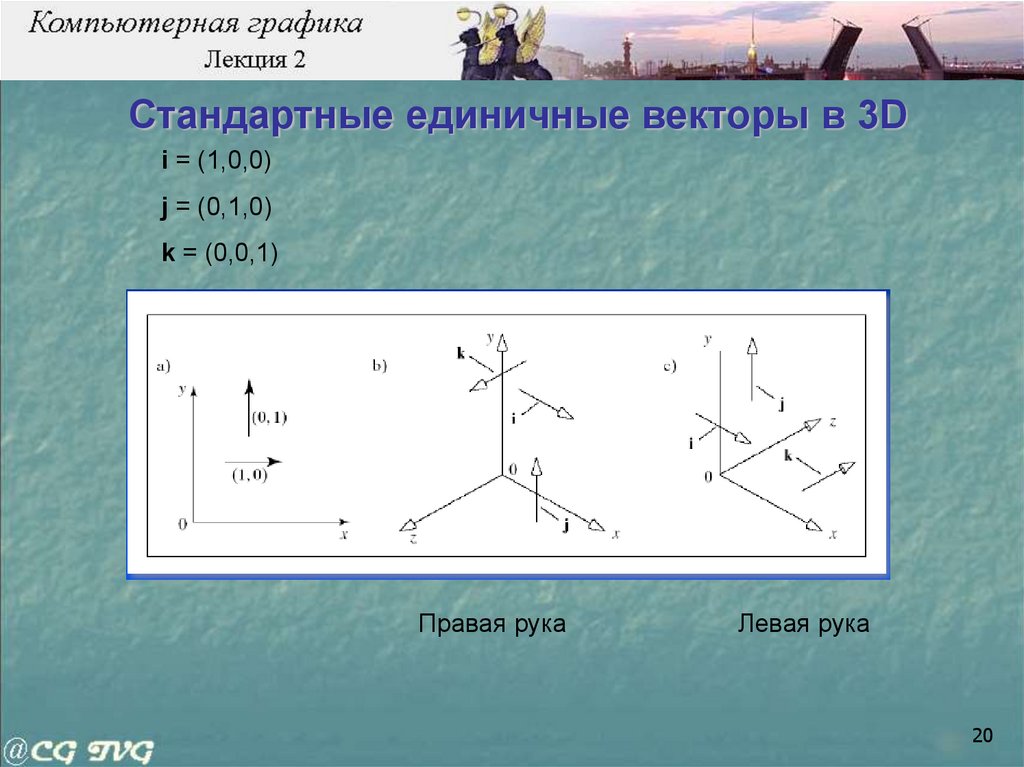
20. Стандартные единичные векторы в 3D
i = (1,0,0)j = (0,1,0)
k = (0,0,1)
Правая рука
Левая рука
20
21. Линии
• форма наклонной, сточками пересечения
• y = mx + b
• неявная форма
• y – mx – b = 0
• Ax + By + C = 0
• f(x,y) = 0
21
22. Окружность
f ( x, y ) ( x xc ) ( y yc ) r
2
2
2
• окружность – это точки (x,y), где f(x,y) = 0
p ( x, y ), c ( xc , yc ) : (p c) (p c) r 2 0
• точки p на окружности имеют свойство, что вектор
из c в p дает скалярное произведение r2
p c r 0
2
2
• точки p на окружности имеют свойство, что
квадрат расстояния из c в p - r2
p c r 0
• точки p на окружности – расстоние r из центра c
22
23. Параметрические кривые
• Параметр: индекс изменяющийсянепрерывно
• (x,y): точка на кривой
• t: параметр
x g (t )
y h(t )
• Вектор из
p f (t )
23
24. 2D параметрическая линия
x x 0 t(x1 x 0 )•
y y 0 t(y1 y 0 )
• p(t ) p 0 t (p1 p 0 )
• p(t ) o t (d)
• Начинается в точке p0,
и идет до p1,
в соответствии с параметром t
• p(0) = p0, p(1) = p1
24
25. Линейная интерполяция
• Параметричекая линия примерследующих общих поняти1
• p(t ) p 0 t (p1 p 0 )
• интерполяция
• p идет через a в t = 0
• p идет через b в t = 1
• линейность
• веса t, (1-t) линейные полиномиалы в t
25
26. Матрицы
• Множество чисел (m×n = m строки, n столбцы)1 3
5
2
0 4
• Сложение, умножение скаляром просто : элемент
за элементом
26
27. Сложение матриц
• сложение: matrix + matrix = matrixm11 m12 n11 n12 n11 m11 n12 m12
m
21 m22 n21 n22 n21 m21 n22 m22
• пример
1 3 2 5 1 ( 2) 3 5 1 8
2 4 7 1 2 7
4 1 9 5
27
28. Умножение скаляр - матрица
• умножение: скаляр * matrix = matrixm11 m12 a * m11 a * m12
a
m21 m22 a * m21 a * m22
• пример
2 4 3 * 2 3 * 4 6 12
3
1 5 3 *1 3 * 5 3 15
28
29. Умножение матрица-матрица
• Можно только умножить (n,k) на (k,m):число левых столбцов = числу правых строк
• разрешено
h i
a b c
e f g j k
l
m
• неопределено
a b c
e f g h i
j k
o p q
29
30.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
30
31.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
31
32.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
32
33.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p12
p22
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
p22 m21n12 m22n22
33
34.
Умножение матрица-матрица• Строка на столбец
m11 m12 n11 n12 p11
m
21 m22 n21 n22 p21
p11 m11n11 m12n21
p21 m21n11 m22n21
p12 m11n12 m12n22
p22 m21n12 m22n22
• некоммутативно: AB != BA
p12
p22
34
35.
Умножение матрица-вектор• точки вектора-столбца: постумножаются
x' m11 m12
y '
m21 m22
z ' m31 m32
h' m41 m42
m13
m23
m33
m43
m14 x
m24 y
m34 z
m44 h
p' Mp
• точки вектора-строка : предумножаются
x'
y ' z ' h' x
y
m11 m12
m21 m22
z h
m31 m32
m41 m42
m13
m23
m33
m43
m14
m24
m34
m44
T
p' p M
T
T
T
35
36.
Умножение матрица-матрицаПример умножения матриц
1 3
9 27 33 13
3 6 9 4
5
2
19
44
61
26
2 7 8 3
0 4
8
28
3
2
1
2
36
37.
Матрицы• транспонированная
m
m
m
11
12
m21 m22
m31 m32
m41 m42
идентичности
1
0
0
0
• обратная
13
m23
m33
m43
0 0
1 0
0 1
0 0
m14
m24
m34
m44
0
0
0
1
T
m11
m
12
m13
m14
m21
m31
m22
m32
m23
m33
m24
m34
m41
m42
m43
m44
AA 1 I
• не все матрицы являются обратимыми
37
38.
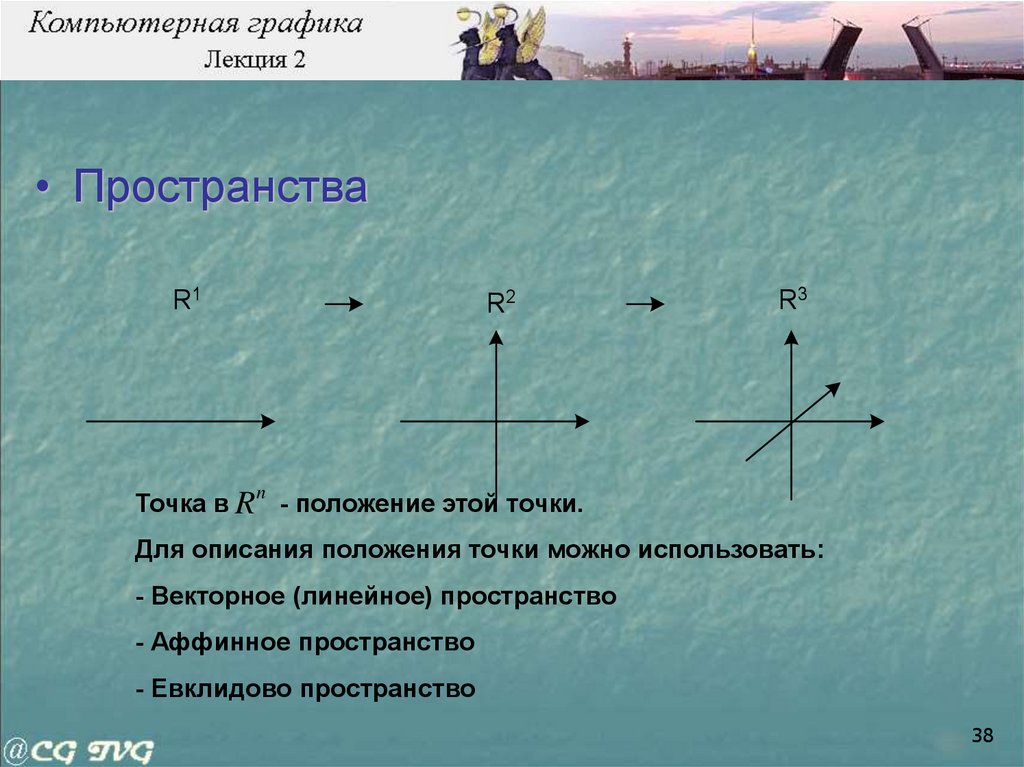
• ПространстваR1
R2
R3
n
Точка в R - положение этой точки.
Для описания положения точки можно использовать:
- Векторное (линейное) пространство
- Аффинное пространство
- Евклидово пространство
38
39.
• Линейное пространство создают скаляры ивекторы.
• Аффинное пространство – добавляется
понятие точки.
• Евклидово пространство – вводят понятие
расстояние.
• Системы координат: Положение точки в
пространстве может быть описано в виде
комбинации некоторых линейно-независимых
векторов .
• Если ввести скаляры , то можно описать вектор
(положение точки) так:
W 1V1 2V2 3V3
39
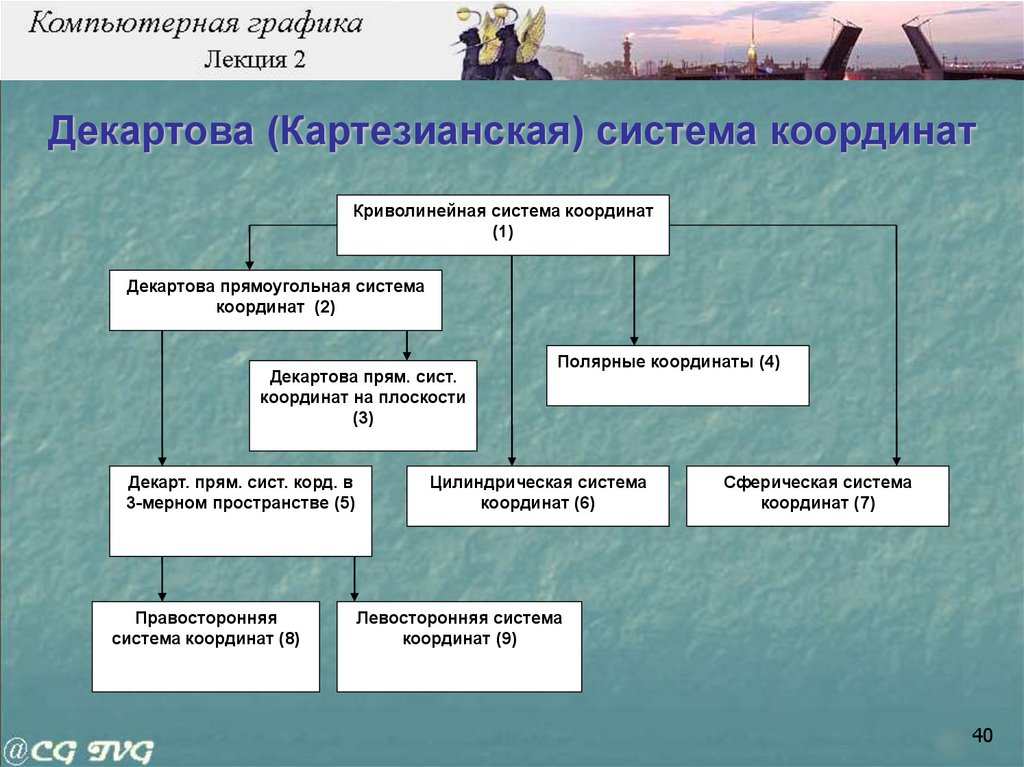
40.
Декартова (Картезианская) система координатКриволинейная система координат
(1)
Декартова прямоугольная система
координат (2)
Декартова прям. сист.
координат на плоскости
(3)
Декарт. прям. сист. корд. в
3-мерном пространстве (5)
Правосторонняя
система координат (8)
Полярные координаты (4)
Цилиндрическая система
координат (6)
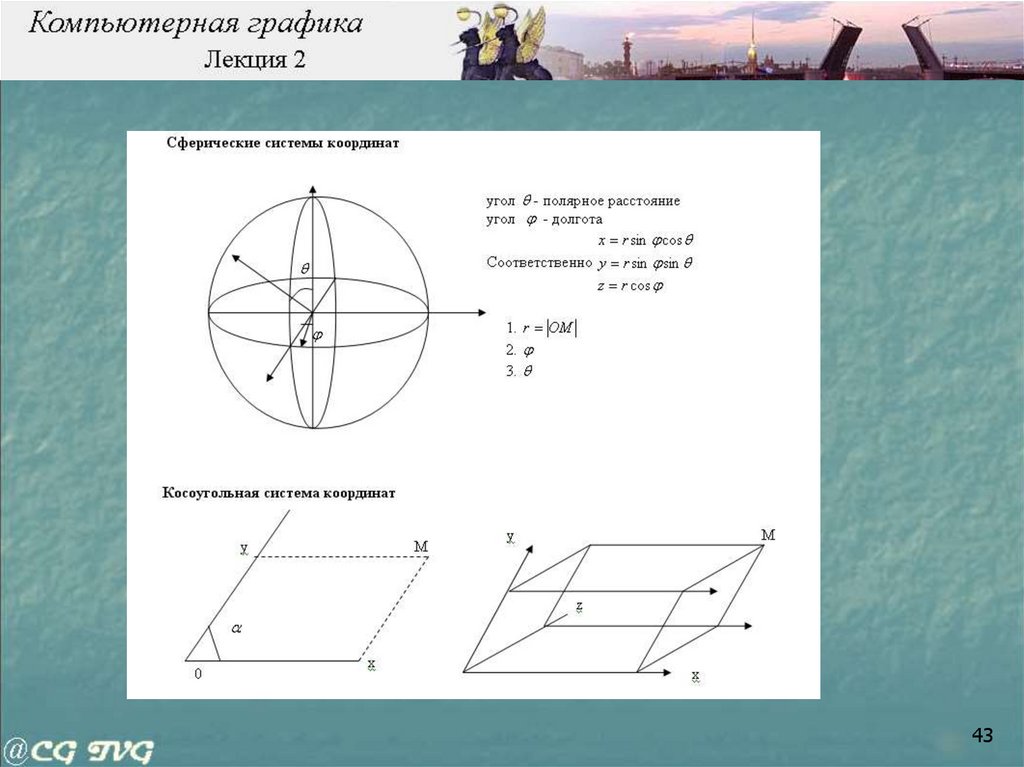
Сферическая система
координат (7)
Левосторонняя система
координат (9)
40
41.
• Базовая косоугольная система координатКоординаты определяются осями ( х – ось абсцисс,
у - ось ординат)
Расстояние определяется проекциями P ( x, y )
• Полярная система координат
Точка О – полюс, - полярный угол , r – полярное
расстояние.
41
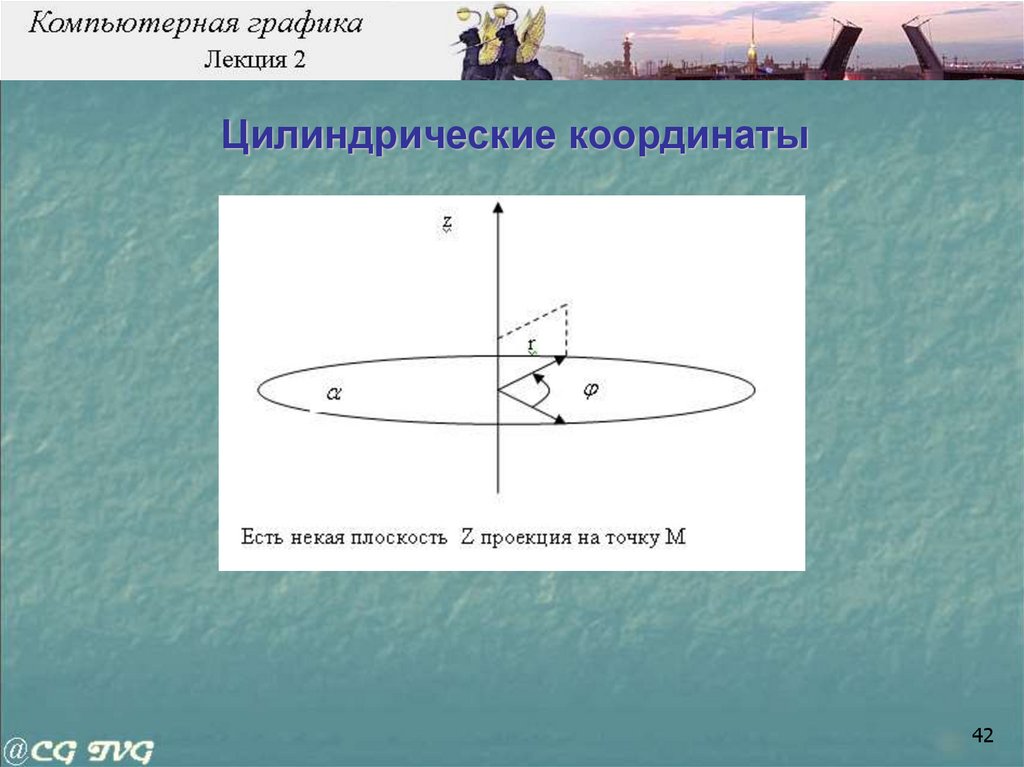
42.
Цилиндрические координаты42



































 mathematics
mathematics








