Similar presentations:
Метод контурных токов
1.
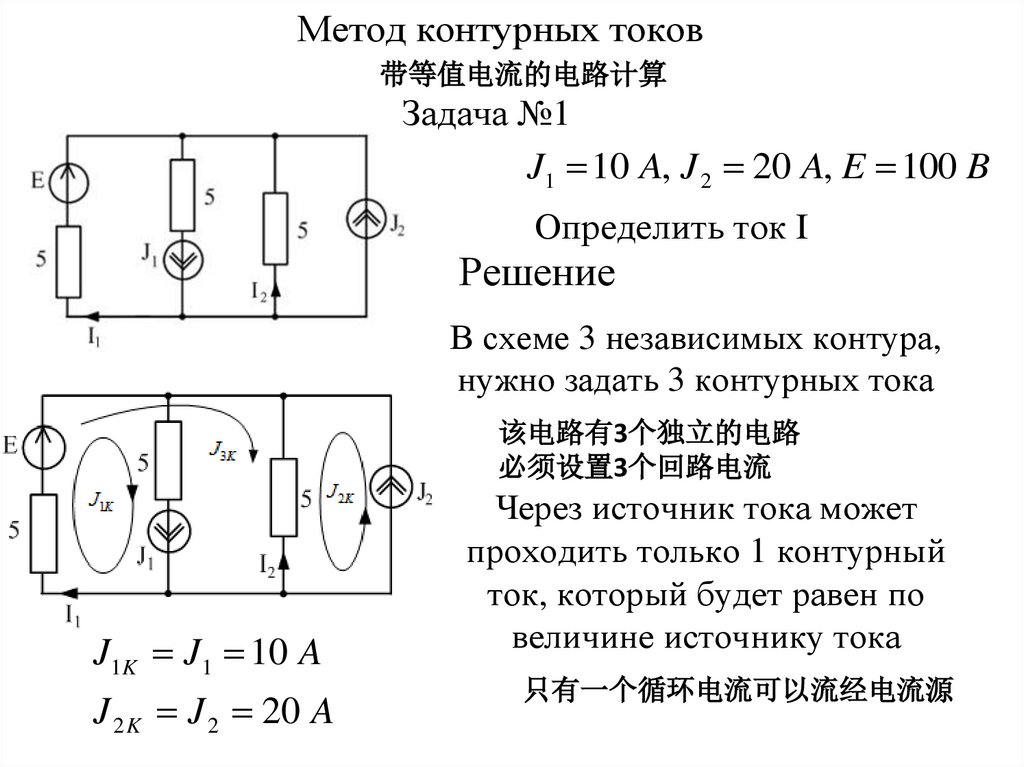
Метод контурных токов带等值电流的电路计算
Задача №1
J1 10 A, J 2 20 A, E 100 B
Определить ток I
Решение
В схеме 3 независимых контура,
нужно задать 3 контурных тока
该电路有3个独立的电路
必须设置3个回路电流
J1K J1 10 A
J 2 K J 2 20 A
Через источник тока может
проходить только 1 контурный
ток, который будет равен по
величине источнику тока
只有一个循环电流可以流经电流源
2.
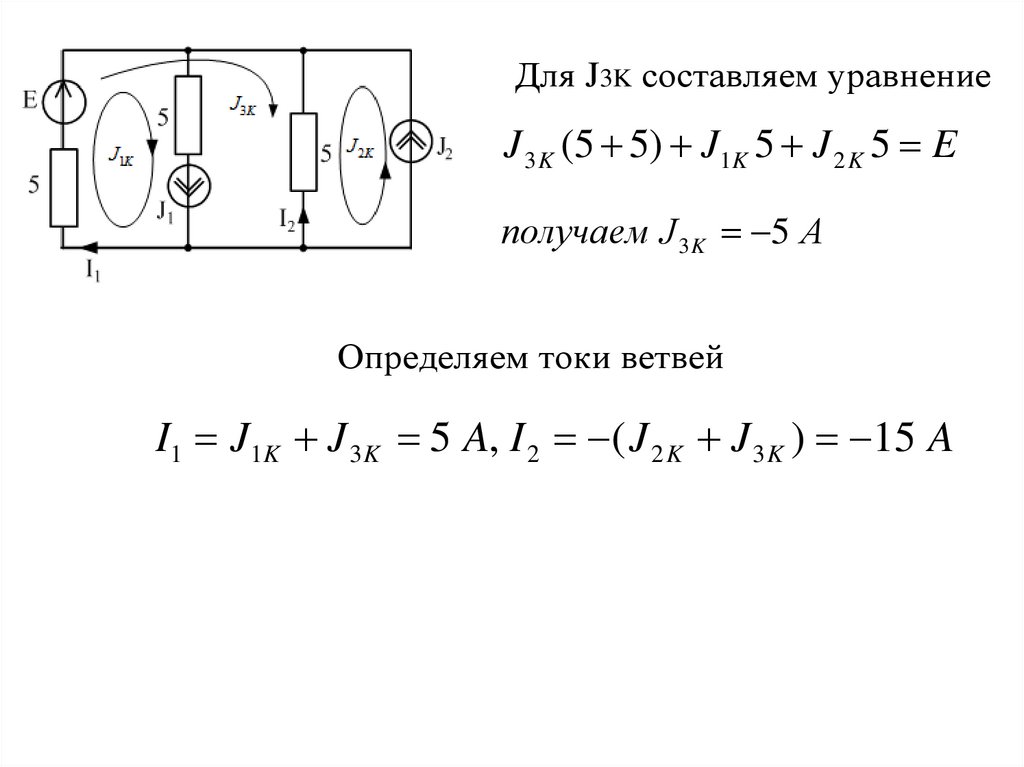
Для J3K составляем уравнениеJ 3 K (5 5) J1K 5 J 2 K 5 E
получаем J 3 K 5 А
Определяем токи ветвей
I1 J1K J 3 K 5 A, I 2 ( J 2 K J 3 K ) 15 A
3.
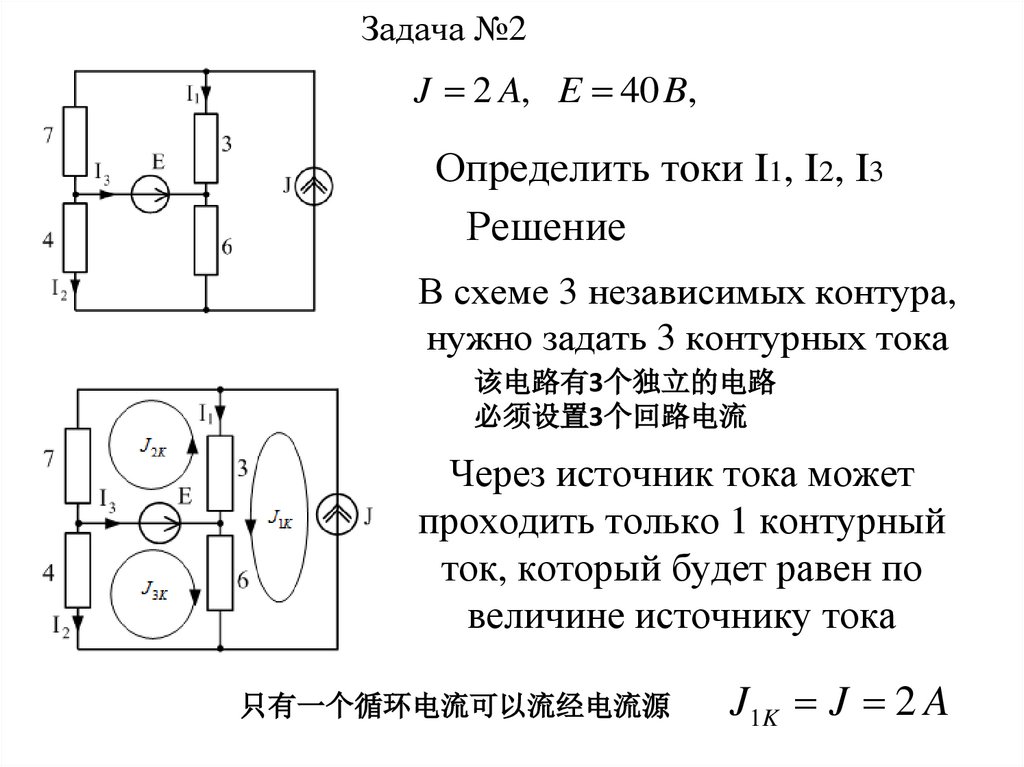
Задача №2J 2 A, E 40 B,
Определить токи I1, I2, I3
Решение
В схеме 3 независимых контура,
нужно задать 3 контурных тока
该电路有3个独立的电路
必须设置3个回路电流
Через источник тока может
проходить только 1 контурный
ток, который будет равен по
величине источнику тока
只有一个循环电流可以流经电流源
J1 K J 2 A
4.
Для J2K и J3K составляем уравнения:J 2 K (7 3 0) J1K 3 J 3 K 0 E
J 3 K (4 6 0) J1K 6 J 2 K 0 E
RE 0
получаем J 2 K 4.6 А, J 3 K 2.8 А
Определяем токи ветвей
电路分支电流
5.
Задача №3J 2 A, E1 26 B, E2 24 B
Определить токи I1, I2, I3, I4
Решение
В схеме 3 независимых контура,
нужно задать 3 контурных тока
Через источник тока может
проходить только 1 контурный
ток, который будет равен по
величине источнику тока
J 3K J 2 A
Составляем уравнения для
неизвестных контурных токов
6.
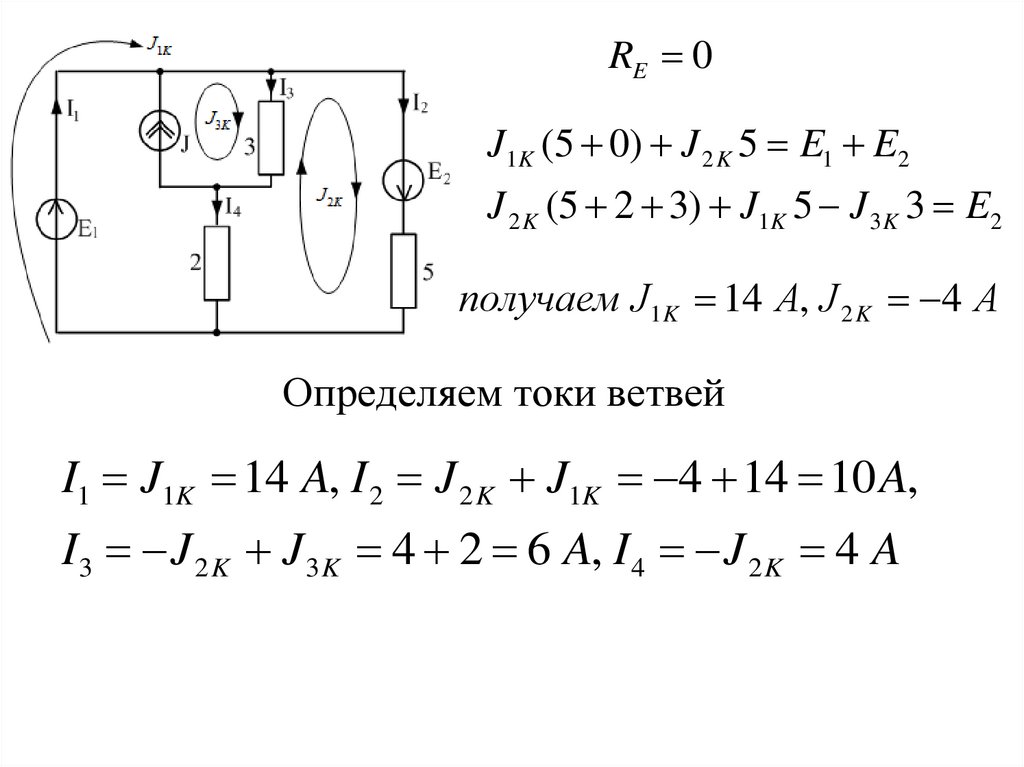
RE 0J1K (5 0) J 2 K 5 E1 E2
J 2 K (5 2 3) J1K 5 J 3 K 3 E2
получаем J1K 14 А, J 2 K 4 А
Определяем токи ветвей
I1 J1K 14 A, I 2 J 2 K J1K 4 14 10 A,
I3 J 2 K J 3 K 4 2 6 A, I 4 J 2 K 4 A
7.
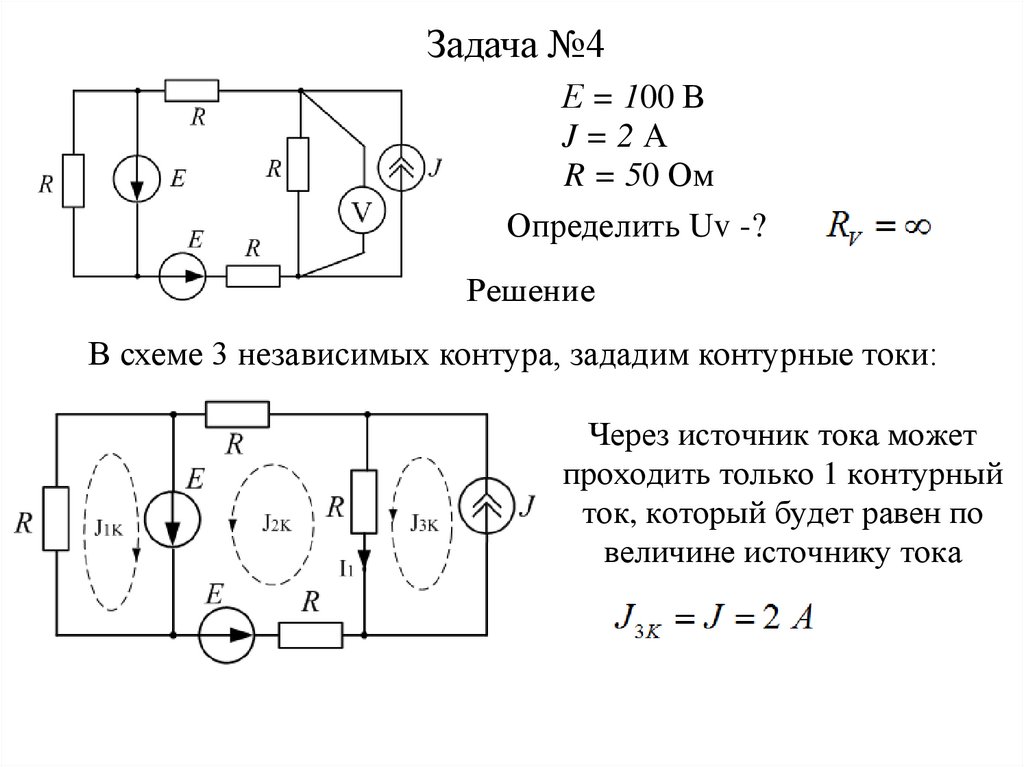
Задача №4Е = 100 В
J=2А
R = 50 Ом
Определить Uv -?
Решение
В схеме 3 независимых контура, зададим контурные токи:
Через источник тока может
проходить только 1 контурный
ток, который будет равен по
величине источнику тока
8.
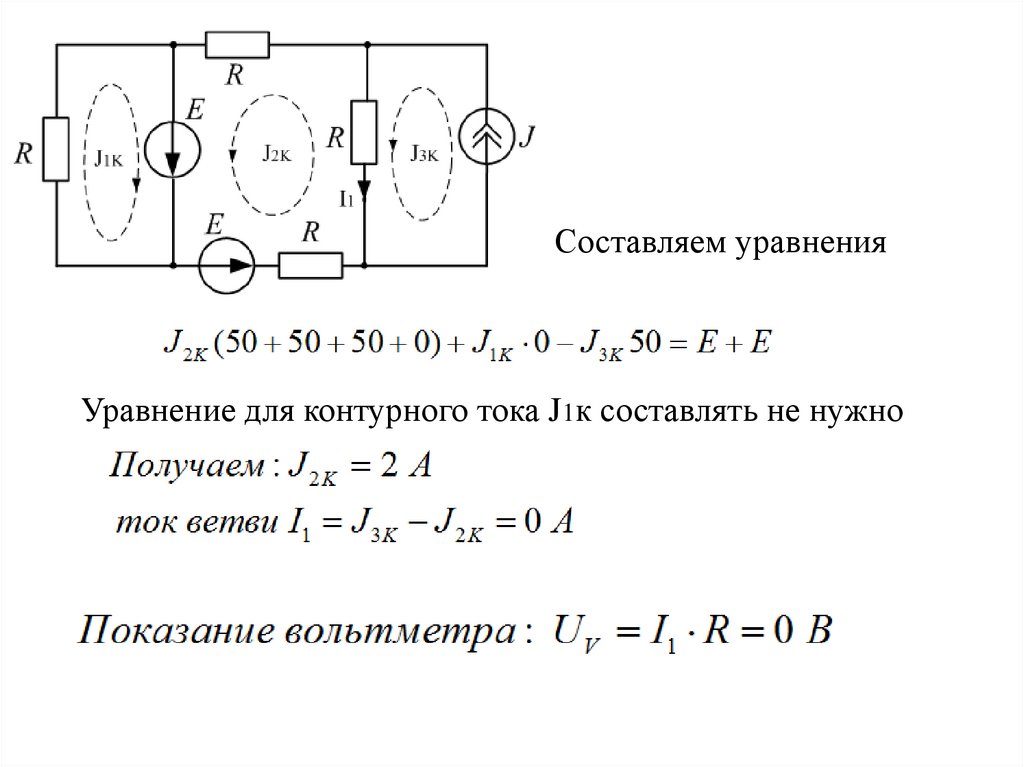
Составляем уравненияУравнение для контурного тока J1к составлять не нужно
9.
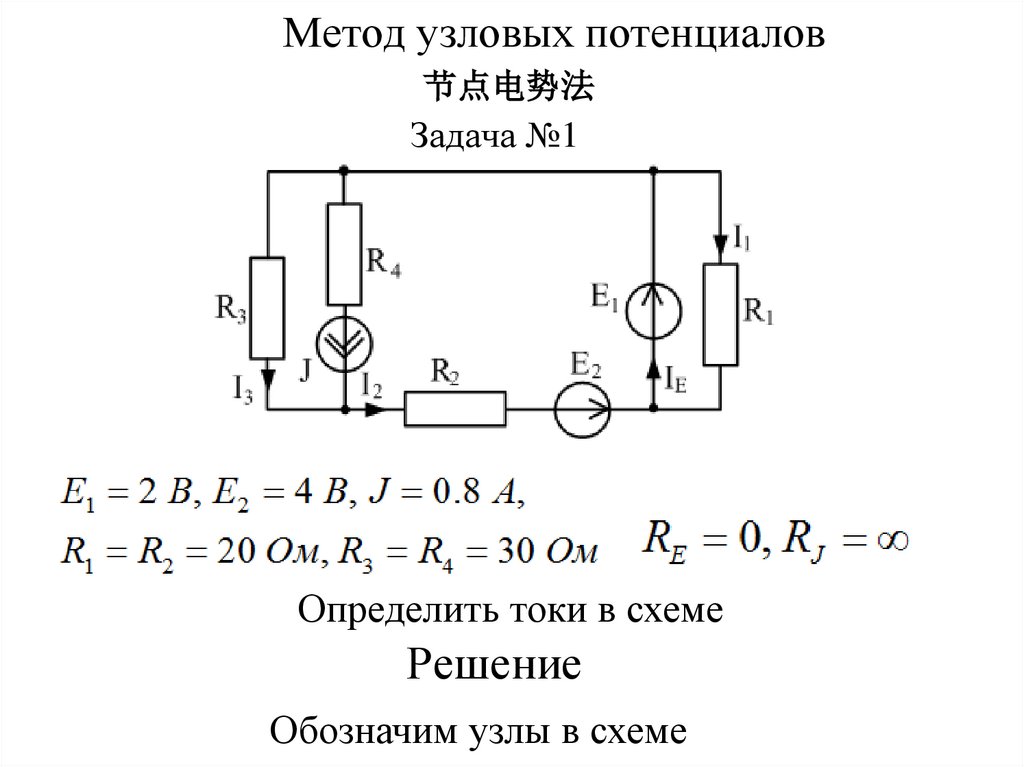
Метод узловых потенциалов节点电势法
Задача №1
Определить токи в схеме
Решение
Обозначим узлы в схеме
10.
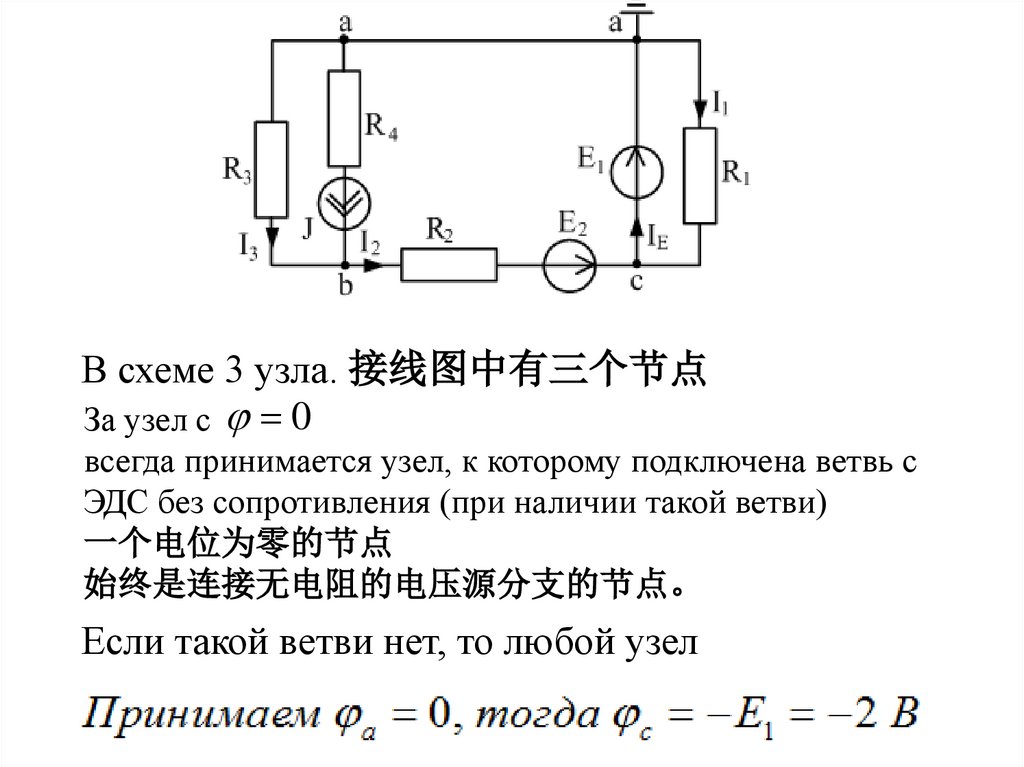
В схеме 3 узла. 接线图中有三个节点За узел с 0
всегда принимается узел, к которому подключена ветвь с
ЭДС без сопротивления (при наличии такой ветви)
一个电位为零的节点
始终是连接无电阻的电压源分支的节点。
Если такой ветви нет, то любой узел
11.
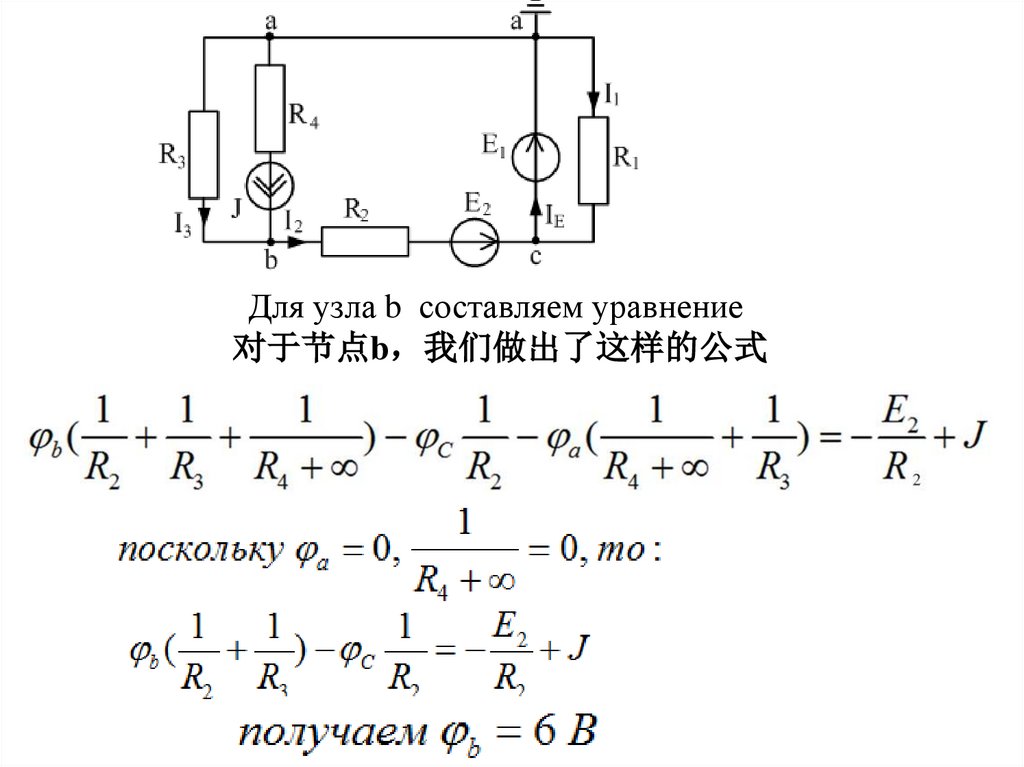
Для узла b составляем уравнение对于节点b 我们做出了这样的公式
12.
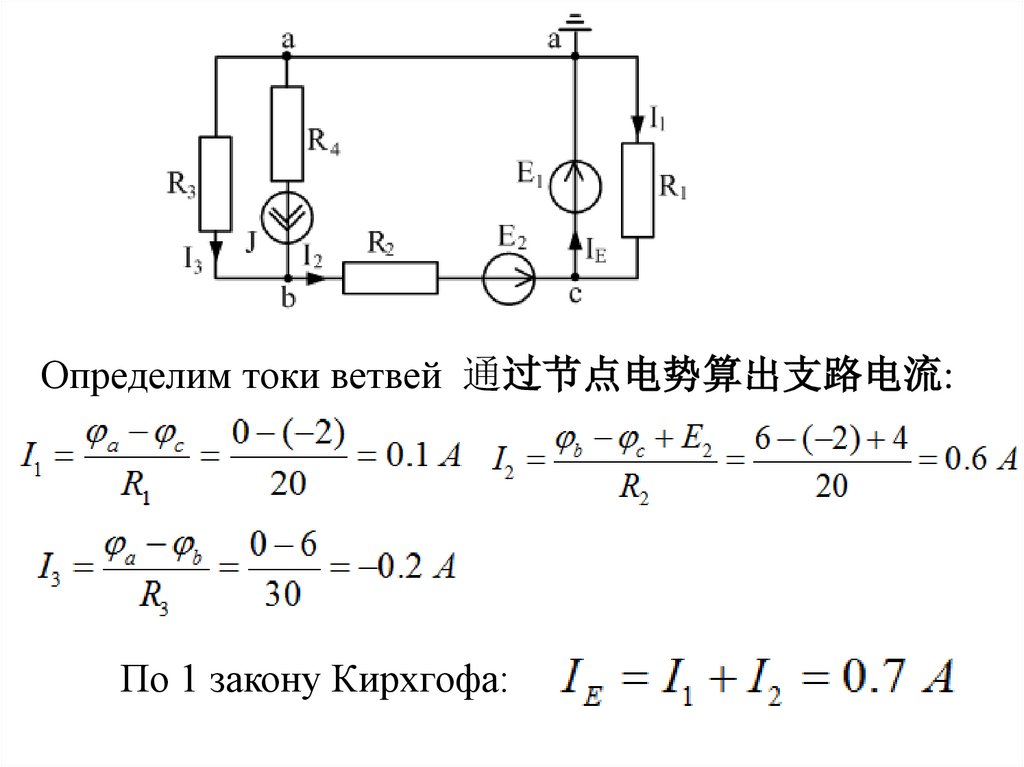
Определим токи ветвей 通过节点电势算出支路电流:По 1 закону Кирхгофа:
13.
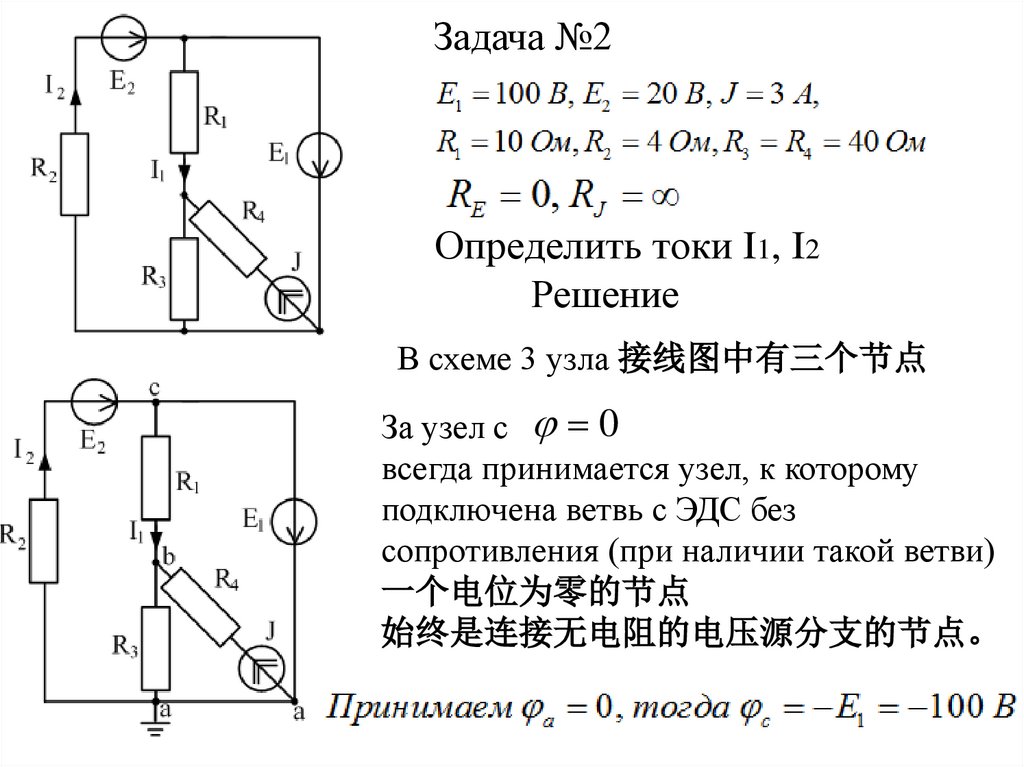
Задача №2Определить токи I1, I2
Решение
В схеме 3 узла 接线图中有三个节点
За узел с 0
всегда принимается узел, к которому
подключена ветвь с ЭДС без
сопротивления (при наличии такой ветви)
一个电位为零的节点
始终是连接无电阻的电压源分支的节点。
14.
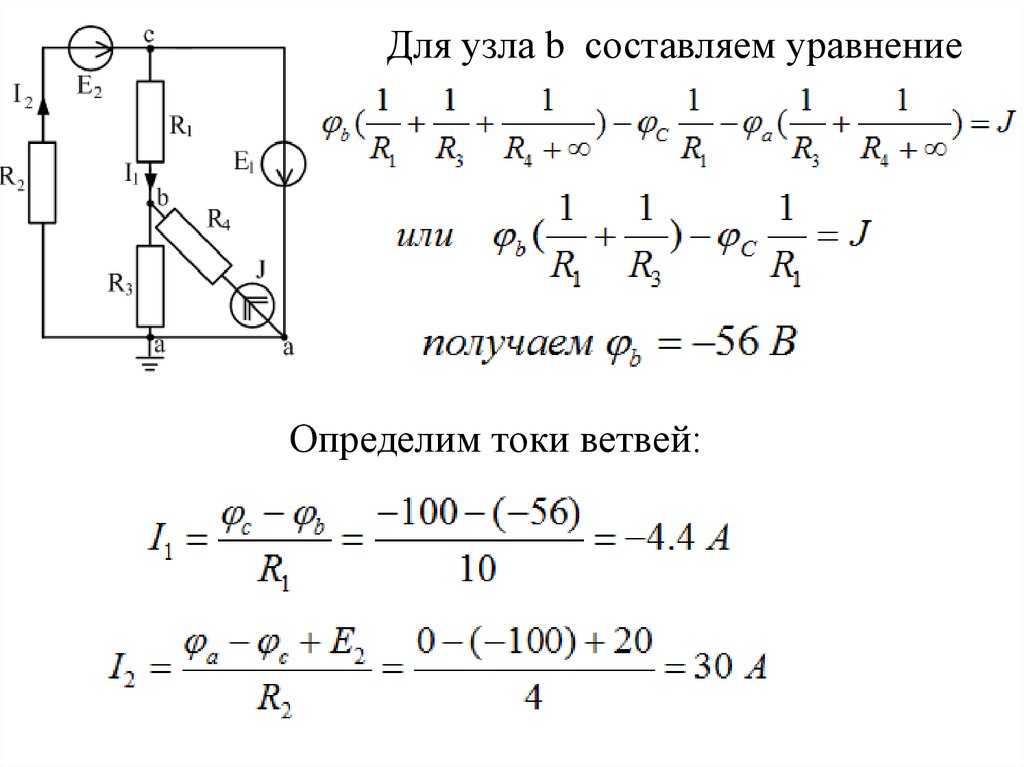
Для узла b составляем уравнениеОпределим токи ветвей:
15.
Задача №3E1 =400 В
Е2=200 В
R=100 Ом
Определить UV ?
Решение
Обозначим узлы в схеме
Принимаем а 0
Показание вольтметра 电压表读数:
16.
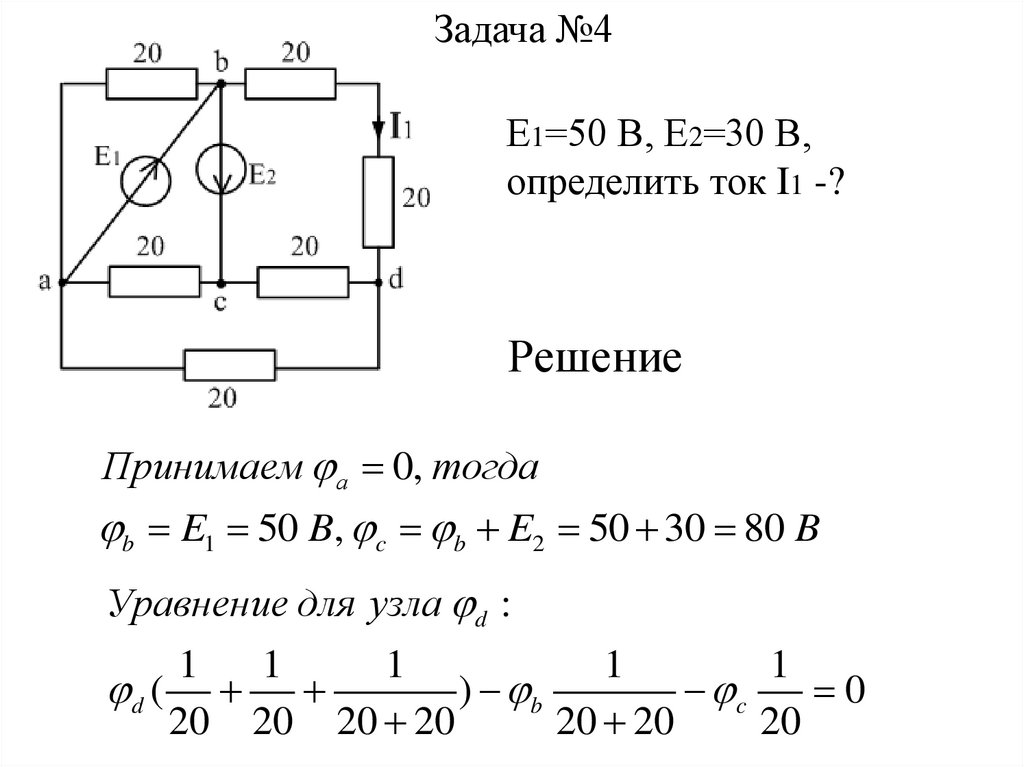
Задача №4Е1=50 В, Е2=30 В,
определить ток I1 -?
Решение
Принимаем а 0, тогда
b E1 50 B, c b E2 50 30 80 B
Уравнение для узла d :
1
1
1
1
1
d (
) b
c
0
20 20 20 20
20 20
20
17.
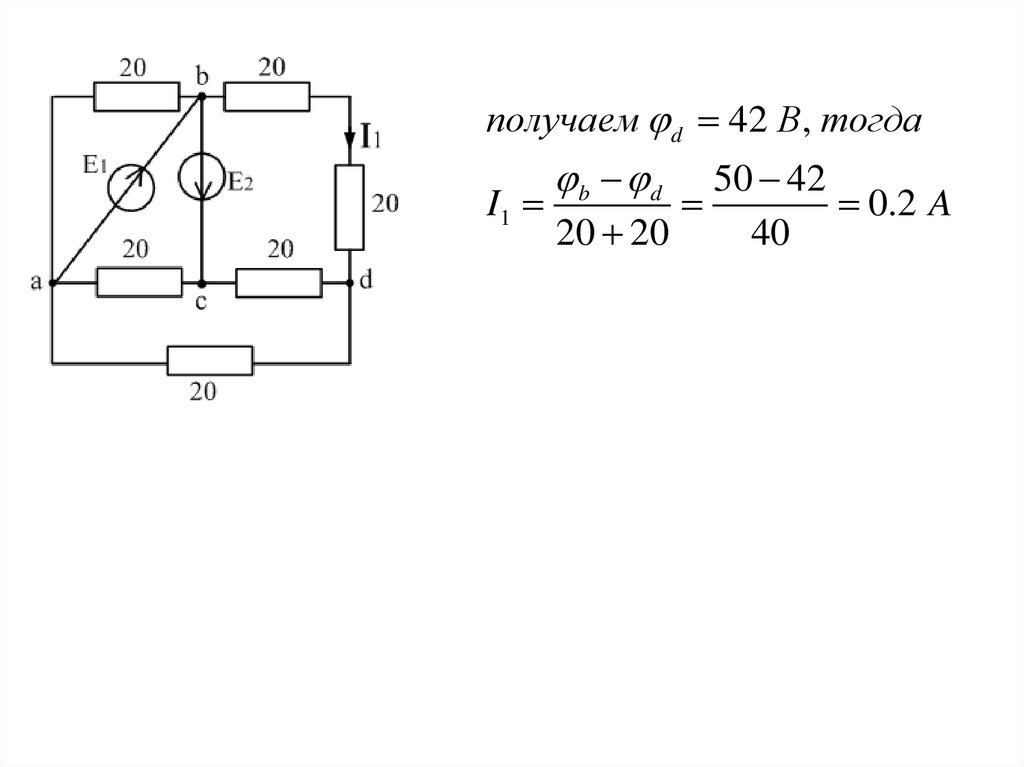
получаем d 42 B, тогдаb d
50 42
I1
0.2 A
20 20
40
18.
Метод преобразования电路的等效转换方法
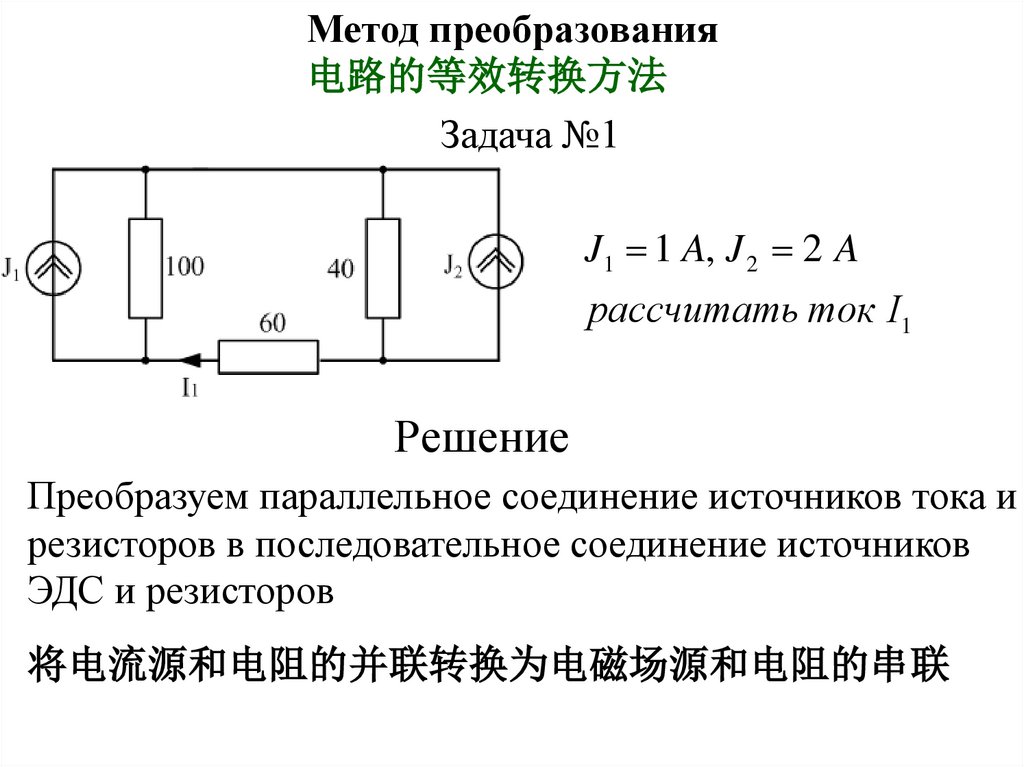
Задача №1
J1 1 A, J 2 2 A
рассчитать ток I1
Решение
Преобразуем параллельное соединение источников тока и
резисторов в последовательное соединение источников
ЭДС и резисторов
将电流源和电阻的并联转换为电磁场源和电阻的串联
19.
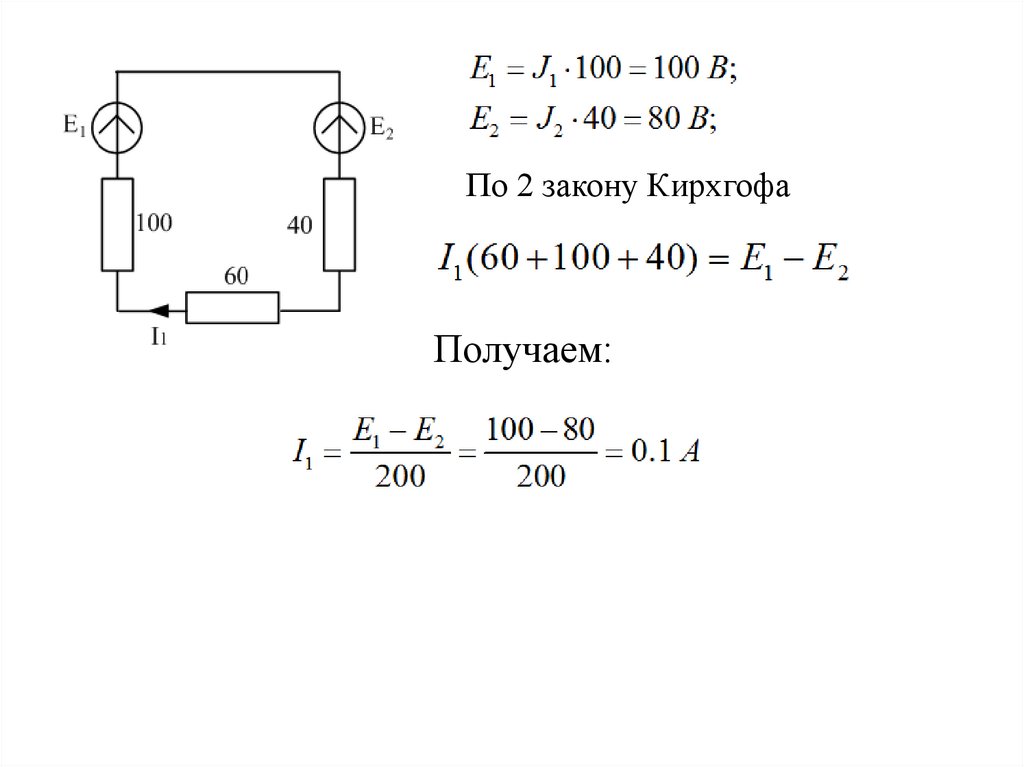
По 2 закону КирхгофаПолучаем:
20.
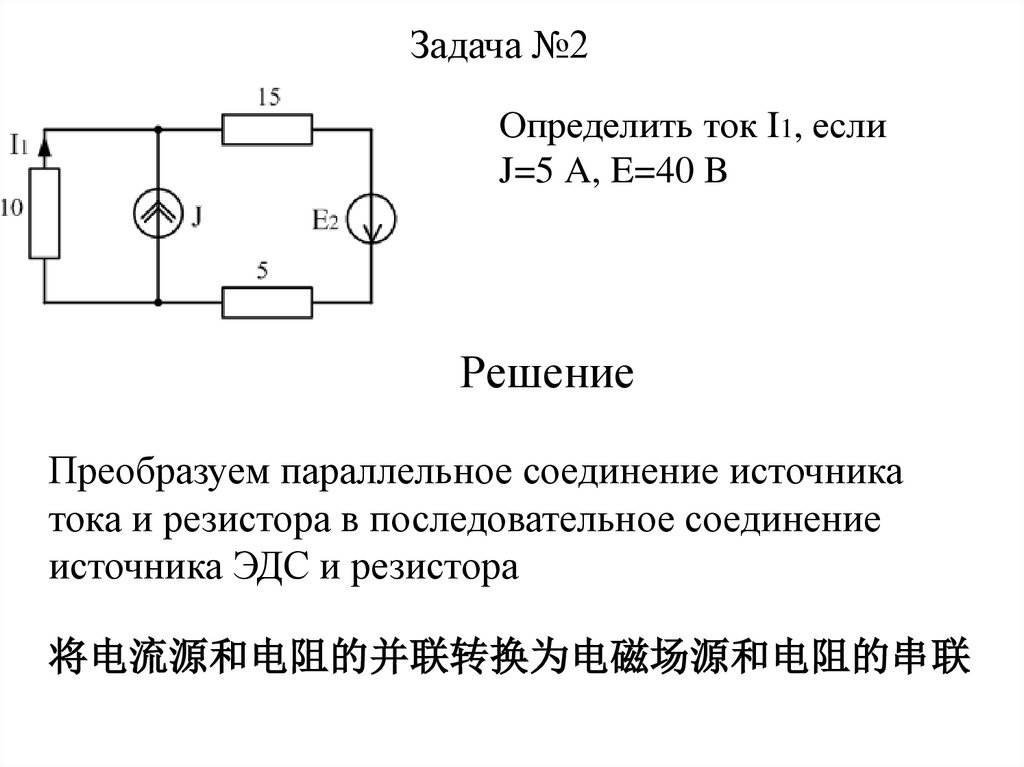
Задача №2Определить ток I1, если
J=5 A, E=40 B
Решение
Преобразуем параллельное соединение источника
тока и резистора в последовательное соединение
источника ЭДС и резистора
将电流源和电阻的并联转换为电磁场源和电阻的串联
21.
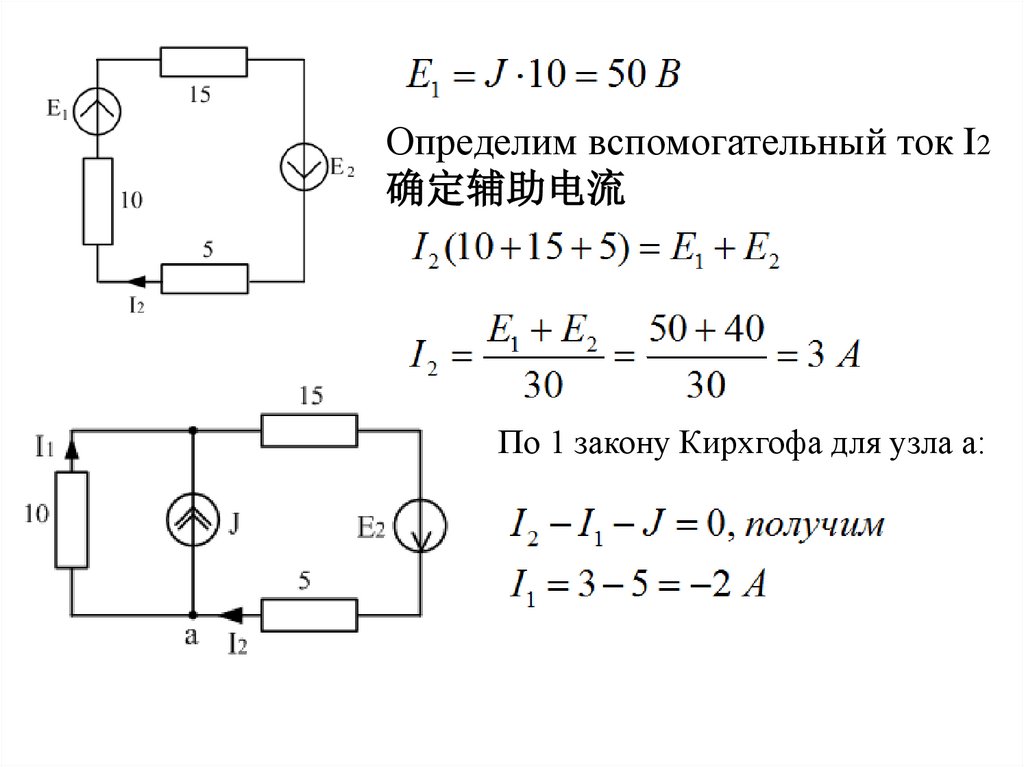
Определим вспомогательный ток I2确定辅助电流
По 1 закону Кирхгофа для узла а:
22.
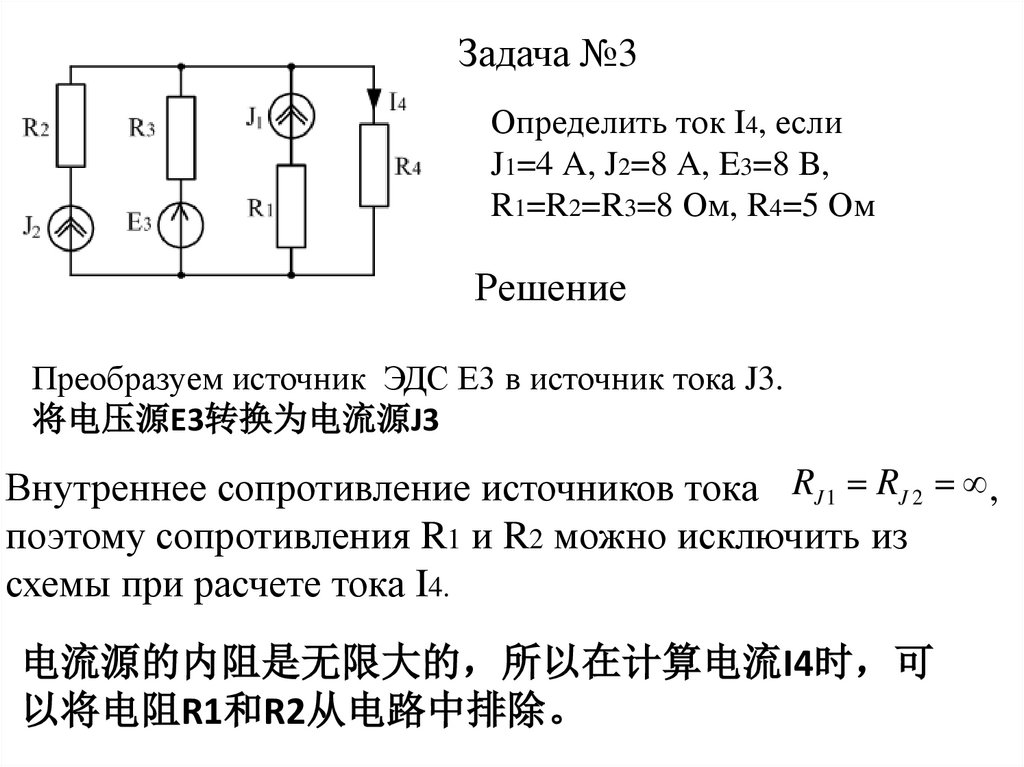
Задача №3Определить ток I4, если
J1=4 A, J2=8 A, E3=8 B,
R1=R2=R3=8 Ом, R4=5 Ом
Решение
Преобразуем источник ЭДС Е3 в источник тока J3.
将电压源E3转换为电流源J3
Внутреннее сопротивление источников тока RJ 1 RJ 2 ,
поэтому сопротивления R1 и R2 можно исключить из
схемы при расчете тока I4.
电流源的内阻是无限大的 所以在计算电流I4时 可
以将电阻R1和R2从电路中排除。
23.
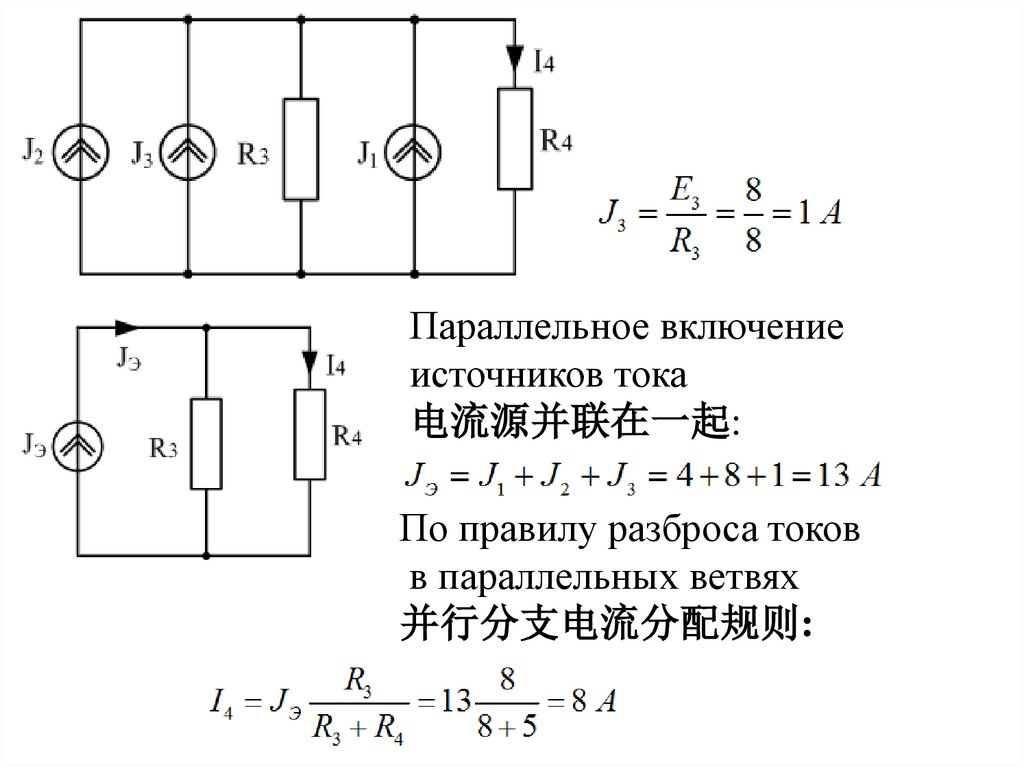
Параллельное включениеисточников тока
电流源并联在一起:
По правилу разброса токов
в параллельных ветвях
并行分支电流分配规则:



 physics
physics








