Квадратичная функция «Функция у = х2»

1. Квадратичная функция

«Функция у = х2»

2. Устный счет

2
3 2
;
7 5
2
1. Вычислите:
2. Функция задана формулой у = 3х – 5.
Найдите у, если х = 0; 1; 2; -2.
3. Функции заданы таблицами. Составьте формулы.
-52;
х 1 2 3 4
у 2 4 6 8
-0,72;
(-0,4)2;
(-9)2;
х 1 2 3 -1 -2 -3
у 1 4 9 1 4 9
4. Принадлежат ли графику функции у = 5х2
точки А(-8; 320), С(-5; -125) ?

3. Определите: возрастает или убывает функция

1
1
0
1
0
1
1
1
0
1
0
1

4.

«График функции у = х2 и ее свойства»
Цели урока
1. Знать, как называется функция вида у = х2.
2. Уметь строить график функции у = х2.
3. Уметь определять свойства функции у = х2.

5. График квадратичной функции носит название парабола

АПОЛЛОНИЙ ПЕРГСКИЙ (расцвет деятельности – вторая
половина 2 в. до н.э.), древнегреческий математик родом из
Перги в Памфилии, прозванный современниками Великим
геометром. Занимался математикой в Александрии под
руководством учеников Эвклида.
д
р
п
Аполлоний ввел понятия параболы и
дал ее теорию, сохранившуюся в
практически неизменном виде до
эпохи Ньютона.

6. Примеры парабол в технике, природе и жизни

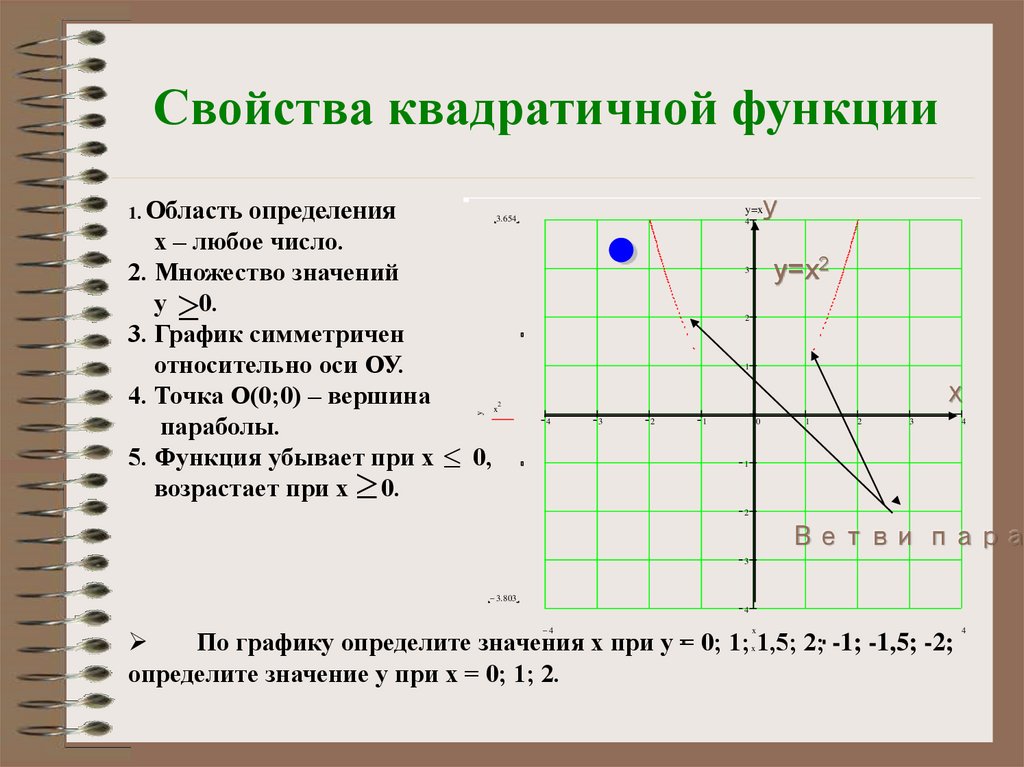
7. Свойства квадратичной функции

1. Область
у
y=x
3.654
4
у=х2
3
2
1
х
2
x
y
определения
х – любое число.
2. Множество значений
у 0.
3. График симметричен
относительно оси ОУ.
4. Точка О(0;0) – вершина
параболы.
5. Функция убывает при х
возрастает при х 0.
4
0,
3
2
1
0
1
2
3
4
1
2
Ветви пара
3
3.803
4
4
x
По графику определите значения х при у = 0; 1; 1,5; 2; -1; -1,5; -2;
определите значение у при х = 0; 1; 2.
x
4

8. Самостоятельная работа в парах по плану

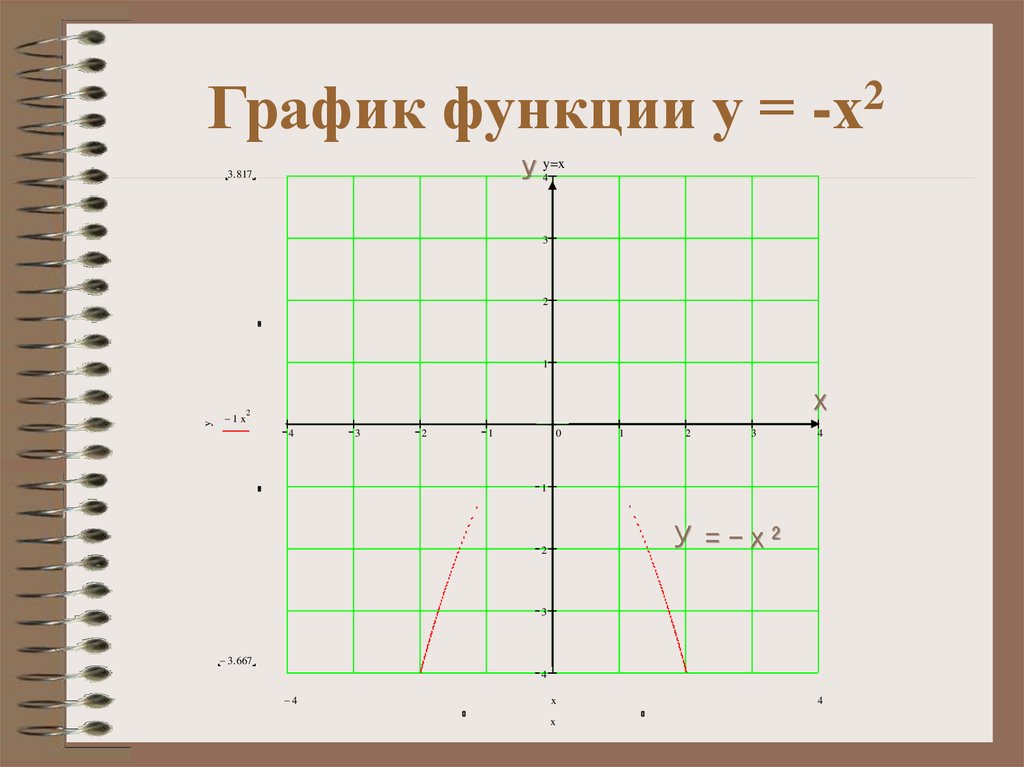
1. Постройте график функции у = -х2;
2. Определите свойства функции у = -х2:
-
Область определения;
Множество значений;
Симметричность графика функции;
Координаты вершины;
Возрастание, убывание функции.
3. Оцените свою работу.

9. График функции у = -х2

уy=x
3.817
4
3
2
1
х
y
2
1 x
4
3
2
1
0
1
2
3
4
1
У = -х2
2
3
3.667
4
4
x
x
4

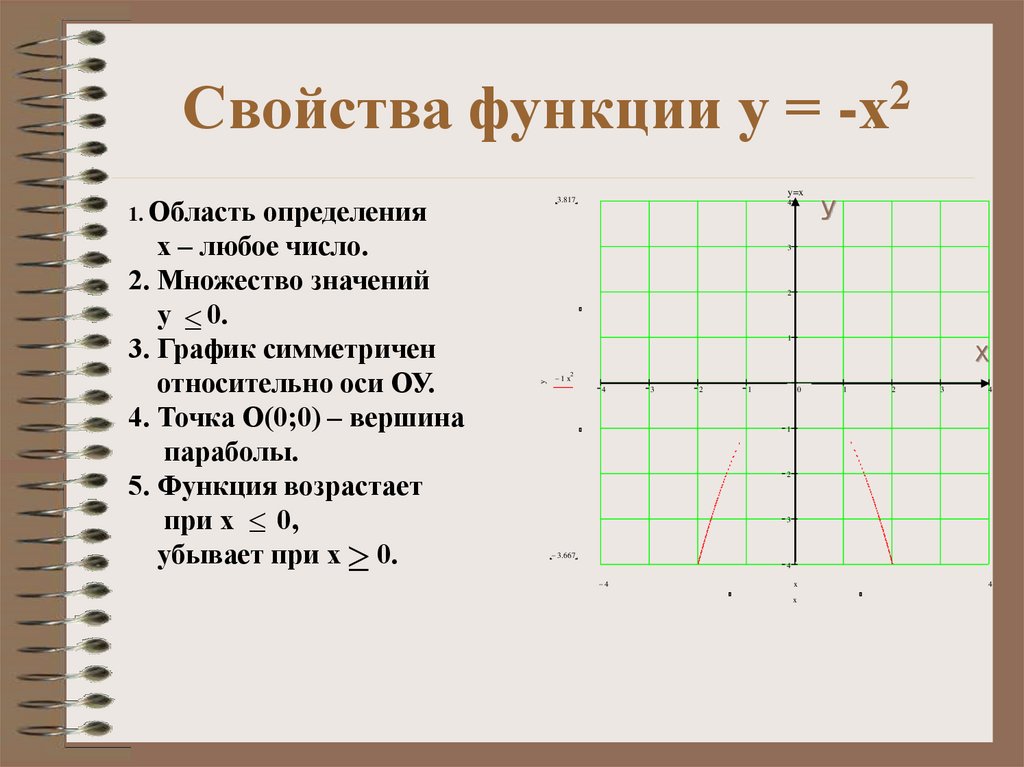
10. Свойства функции у = -х2

1. Область
4
у
3
2
1
х
2
y
определения
х – любое число.
2. Множество значений
у 0.
3. График симметричен
относительно оси ОУ.
4. Точка О(0;0) – вершина
параболы.
5. Функция возрастает
при х 0,
убывает при х 0.
y=x
3.817
1 x
4
3
2
1
0
1
2
3
4
1
2
3
3.667
4
4
x
x
4