Равносильные формулы. Уроки 17-18

1.

Уроки 15-16.
.
Равносильные
формулы.

2.

1
Вопросы.
.
1)Что такое формула алгебраических высказываний?
2)Из чего состоит формула алгебраических высказываний?
3)Как определить истинна или ложна формула
алгебраических высказываний?
4)Записать порядок старшинства действий с простейшими
высказываниями.
5)Записать значения переменных в таблице истинности
формулы, если переменных одна.
6) Записать значения переменных в таблице истинности
формулы, если переменных две.
7) Записать значения переменных в таблице истинности
формулы, если переменных три.

3.

2
Равносильные формулы.
.
Две формулы алгебры логики называются
равnносильными, если они принимают
одинаковые логические значения на любом
наборе значений входящих в них элементарных
высказываний.
Равносильность формул F1 и F2
обозначается как F1 F2 .

4.

3
Пример.
.
Доказать равносильность А В А В.
Доказательство.
Обозначения А В А В . Строим таблицу
m
A
0
0
1
1
B m A
0
1
0
1
n
n
m n

5.

.
4
Возведение и извлечение.
Для числа z r cos i sin верны формулы:
1) z n r n cos n i sin n ;
2)
n
2 k
2 k
z r cos
i sin
,
n
n
где k 0,1, 2,...n -1.
n

6.

.
5
Примеры
Возвести и извлечь.
1) z 3 cos 39 i sin 39 ,
z ,
2) z cos 50 i sin 50 ,
z , z ?
5
3
z ?
4 5
3) z 8 cos120 i sin120 , z , z ?
2 3

7.

.
Примеры.
6
Вычислить.
1) 2 cos 32 i sin 32 ;
5
2) cos 72 i sin 72 ;
4
3)
4
3 cos100 i sin100 ;
4) 1 i .
20

8.

.
7
Повторение.
2 4
2
3
1) Вычислить: arcsin
arccos
5arcsin
;
2
2 3
2
2) Решить систему:
7
3
x 112 x 0,
3
3
0;
2
x
2
x
4
x
1
3) Решить неравенство: log 1 log 2 log 5 x .
3
8

9.

Учебная
работа.
8
1)Составить конспект.
2)Ответить на
вопросы.
3)Разобрать слайды 2,3.

10.

.

11.

1
Законы равносильности и нуля с
единицей.
.
1) Законы равносильности:
x x x
x x x
x x 0
x x 1
2) Законы нуля и единицы:
x 1 x
x 1 1
x 0 0
x 0 x.

12.

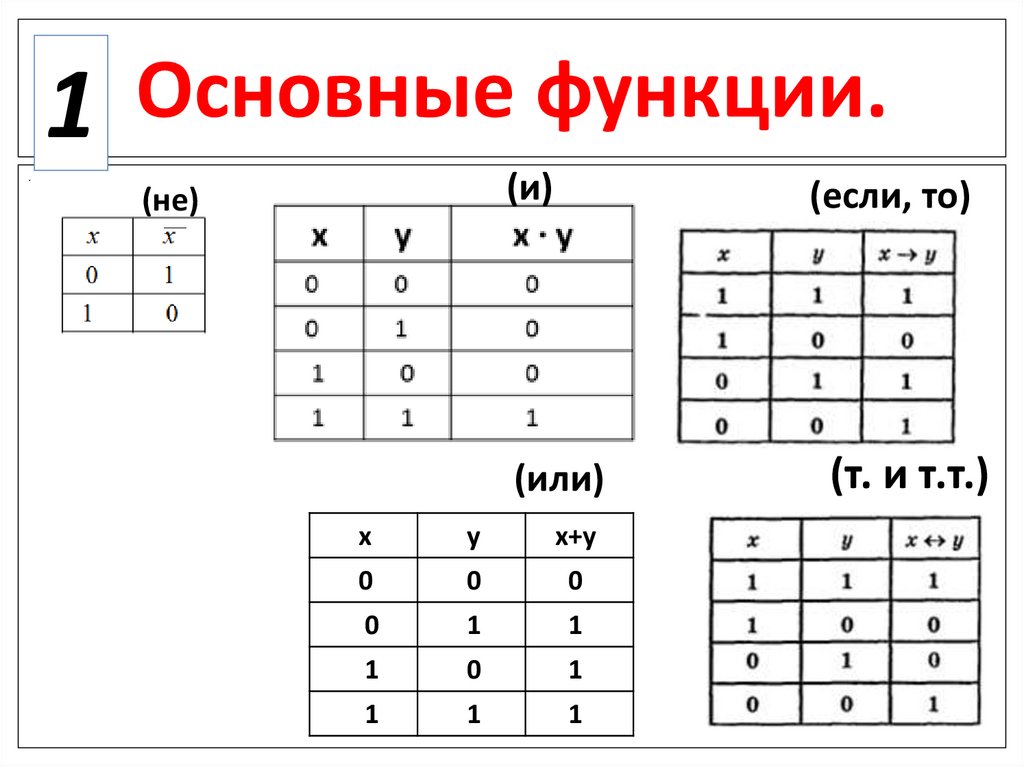
1
Основные функции.
(и)
.
(не)
(если, то)
(или)
x
y
x+y
0
0
0
0
1
1
1
0
1
1
1
1
(т. и т.т.)

13.

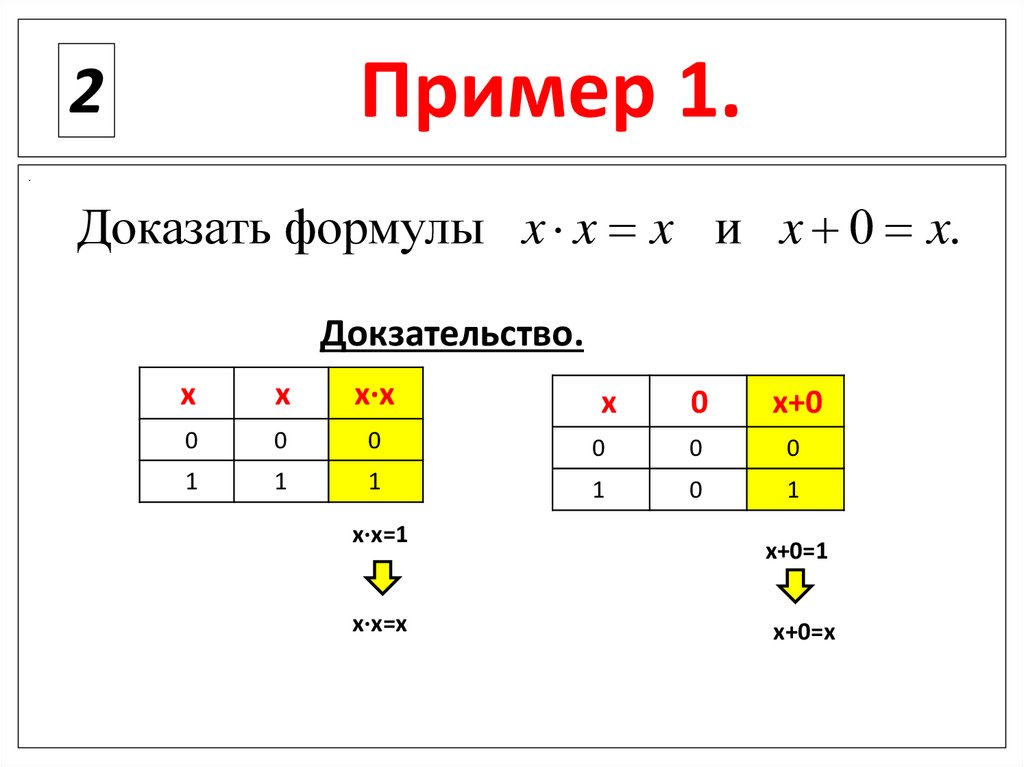
Пример 1.
2
.
Доказать формулы x x x и x 0 x.
Докзательство.
х
х
х∙х
0
0
0
1
1
1
х∙х=1
х∙х=х
х
0
х+0
0
0
0
1
0
1
х+0=1
х+0=х

14.

3 Умножение в тригонометрической форме.
.
Для двух комплексных чисел
z1 r1 cos 1 i sin 1 ;
z2 r2 cos 2 i sin 2 ,
верны действия:
z1 z 2 r1 r2 cos 1 2 i sin 1 2 .

15.

.
4
Пример 2.
Умножить z1 = 3 cos 70 i sin 70 на
z 2 =2 cos 30 i sin 30 .

16.

6
Учебная работа.
1.Число.
2.Фамилия, группа № …
3.Учебная работа.
4.Карта № …
5.Задания …

17.

.

18.

.

19.

.