Similar presentations:
Специфика проверки и оценивания задач ЕГЭ по математике с развернутым ответом. Вопросы теории равносильности
1. Специфика проверки и оценивания задач ЕГЭ по математике с развернутым ответом. Вопросы теории равносильности при решении
уравнений и неравенствКовалева Галина Ивановна,
доктор пед.наук, директор центра
математического образования
ВГАПО
Волгоград
2019
2.
Структура КИМов ЕГЭ по математике.Профильный уровень
Всего 19 заданий: из них 12 не требуют
развернутого ответа, 7 заданий с
развернутым ответом.
По сравнению с прошлым годом не
изменились критерии оценивания заданий
с развернутым ответом.
Сохранилось разделение заданий с
развернутым ответом по пунктам а), б) ….
3. Тестовая часть
1. Таксист за месяц проехал 11 000 км. Цена бензина 35 рублей залитр. Средний расход бензина на 100 км составляет 7 литров.
Сколько рублей потратил таксист на бензин за этот месяц?
2. На диаграмме показана среднемесячная температура воздуха в
Симферополе за каждый месяц 1988 года. По горизонтали
указываются месяцы, по вертикали – температура в градусах
Цельсия. Определите по приведённой диаграмме наибольшую
среднемесячную температуру в первой половине 1988 года. Ответ
дайте в градусах Цельсия.
86%
93%
4. Тестовая часть
3. На клетчатой бумаге с размером клетки изображена трапеция.Найдите её площадь.
89%
4. В соревнованиях по толканию ядра участвуют спортсмены из
четырёх стран: 4 из Аргентины, 7 из Бразилии, 5 из Парагвая и 4 из 89%
Уругвая. Порядок, в котором выступают спортсмены, определяется
жребием. Найдите вероятность того, что спортсмен, выступающий
первым, окажется из Бразилии.
5. Найдите корень уравнения
3
х 3 3
82%
6. Угол ACO равен 62°. Его сторона CA касается
окружности с центром в точке O. Отрезок CO
пересекает окружность в точке B (см. рис.). 67%
Найдите градусную меру дуги AB окружности,
заключённой внутри этого угла. Ответ дайте в
градусах.
5. Тестовая часть
7. На рисунке изображён график y = f'(x) – производной функции f(x),определённой на интервале (− 9; 3). В какой точке отрезка [− 7; − 5]
функция f(x) принимает наибольшее значение?
33%
8. Через среднюю линию основания треугольной призмы
проведена плоскость, параллельная боковому ребру. Найдите
объём этой призмы, если объём отсечённой треугольной
призмы равен 15.
42%
6. Тестовая часть
9. Найдите значение выражения2
16 5
: 274
90%
59%
11. Заказ на изготовление 323 деталей первый рабочий выполняет на
2 часа быстрее, чем второй. Сколько деталей за час изготавливает
первый рабочий, если известно, что он за час изготавливает на 2
детали больше второго?
12. Найдите наименьшее значение функции
на отрезке 1 ; 5 .
24 24
y 12 x ln 12 x 4
51%
33%
7. Процент невыполнения заданий с развернутым ответом в 2018 году
Всего 6644 участников ЕГЭ профильного уровня.13
14
15
16
17
18
18
77,45
91,42
93,38
98,27
98,20
99,11
97,20
всего выполнили человек
440
120
59
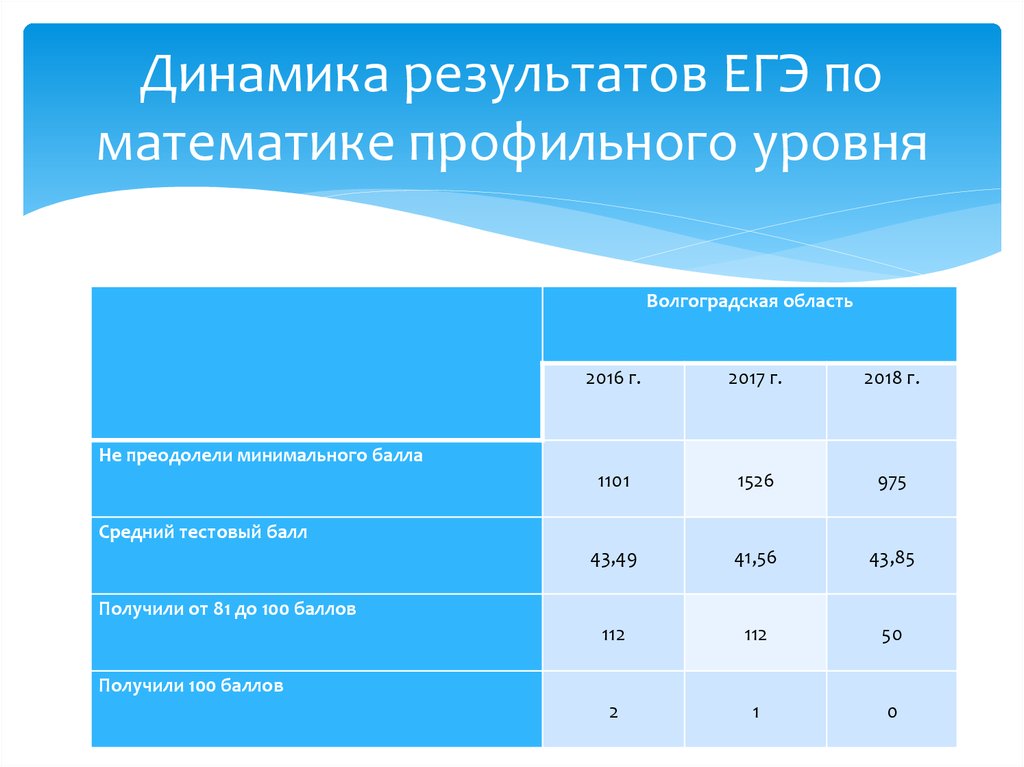
8. Динамика результатов ЕГЭ по математике профильного уровня
Волгоградская область2016 г.
2017 г.
2018 г.
1101
1526
975
43,49
41,56
43,85
112
112
50
2
1
0
Не преодолели минимального балла
Средний тестовый балл
Получили от 81 до 100 баллов
Получили 100 баллов
9. 13. Решение уравнений с выбором ответов
25
принадлежащие промежутку ; .
2
Решите уравнение cos 2 x 1 cos x . Найдите все корни этого уравнения,
а) 1 2 sin 2 x 1 sin x ,
2 sin 2 x sin x 0 ,
sin x 2 sin x 1 0 ,
1
sin x 0 или sin x ,
2
k
x n , n или x 1
б)
С
помощью
k , k .
6
числовой
окружности
5
принадлежащие промежутку ; .
2
отберем
корни
уравнения,
10.
..
Ответ:
а) x n , n ; x 1 k
б) 2 ;
11
7
; .
6
6
6
k , k .
11. Комментарии к критериям
Любые ошибки, допущенные в тригонометрическихформулах, в нахождении значений тригонометрических
функций не относятся к вычислительным.
0 баллов!
sin x 0
x 2πn, n
1
sin x
2
π
x 2πn, n
6
sin x 1
sin x
π
2πn, n
2
cos x
x
1
2
π
πn ,
3
n
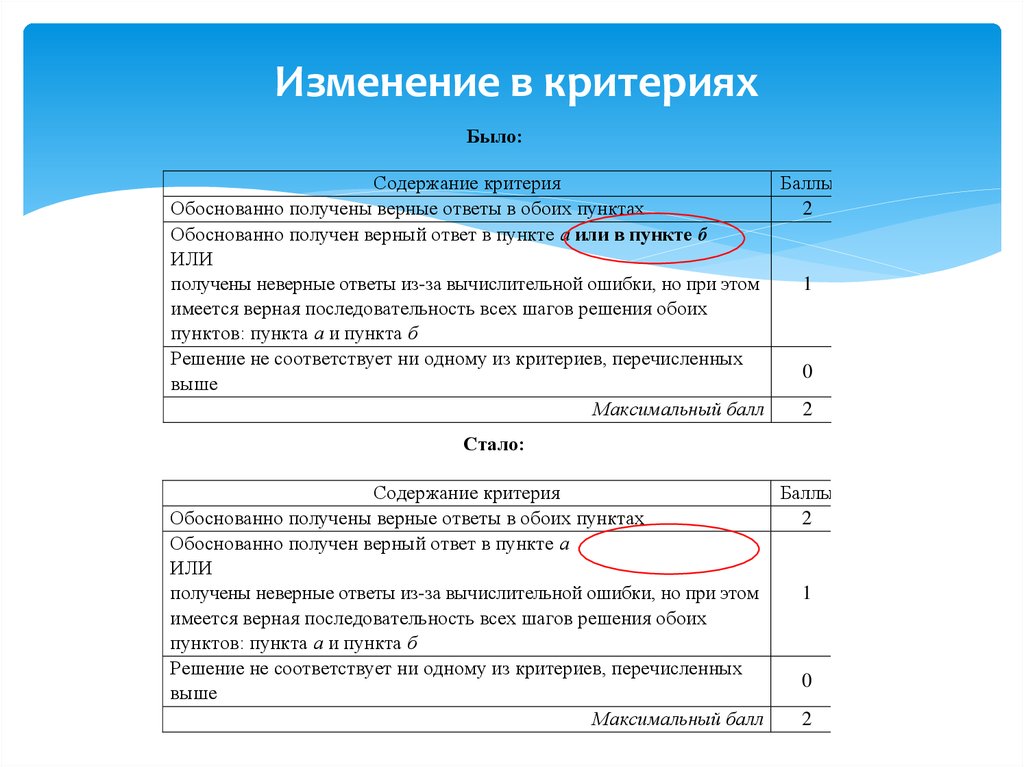
12. Изменение в критериях
Было:Содержание критерия
Баллы
Обоснованно получены верные ответы в обоих пунктах
2
Обоснованно получен верный ответ в пункте а или в пункте б
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом
1
имеется верная последовательность всех шагов решения обоих
пунктов: пункта а и пункта б
Решение не соответствует ни одному из критериев, перечисленных
0
выше
Максимальный балл
2
Стало:
Содержание критерия
Баллы
Обоснованно получены верные ответы в обоих пунктах
2
Обоснованно получен верный ответ в пункте а
ИЛИ
получены неверные ответы из-за вычислительной ошибки, но при этом
1
имеется верная последовательность всех шагов решения обоих
пунктов: пункта а и пункта б
Решение не соответствует ни одному из критериев, перечисленных
0
выше
Максимальный балл
2
13. ОСТОРОЖНО – ОДЗ!
tgx cos 5 x sin 5 x sin 6 xsin x
cos 5 x sin 5 x sin 6 x
cos x
sin x cos 5 x sin 5 x cos x sin 6 x cos x
sin 6 x sin 6 x cos x
sin 6 x (1 cos x) 0
sin 6 x 0
6x k, k Z
x
k
6
,k Z
1 cos x 0
cos x 1
x 2 n, n Z
Оценка эксперта – 0 баллов.
14. ОСТОРОЖНО – ОДЗ!
2 cos x cos x 10
tgx
ОДЗ : cos x 0
2
2 cos 2 x cos x 1 0
cos x 1
x 2 k , k Z
1
cos x
2
x
3
2 n, n Z
Оценка эксперта – 0 баллов.
15. ОСТОРОЖНО – ОДЗ!
4 log 24 (sin 3 x) 8log 2 (sin x) 1ОДЗ : sin x 0
x 0;
log 22 (sin 3 x) 8log 2 (sin x) 1
9 log 22 (sin x) 8log 2 (sin x) 1
log 2 (sin x) t , 9t 2 8t 1 0
log 2 (sin x) 1
sin x
x ( 1) k
6
log 2 (sin x)
1
2
sin x
k, k Z
2
1
9
9
не удов. усл. sin x 1
Оценка эксперта – 0 баллов.
16. РАВНОСИЛЬНЫЕ ПЕРЕХОДЫ
log sin x (8 sin 2 x 3 sin x 3) 18 sin 2 x 3 sin x 3 sin x
sin x 0
sin x 1
8 sin 2 x 2 sin x 3 0
1
sin x
2
x ( 1)
k
6
k , k Z
3
sin x 4
не удов. усл. sin x 0
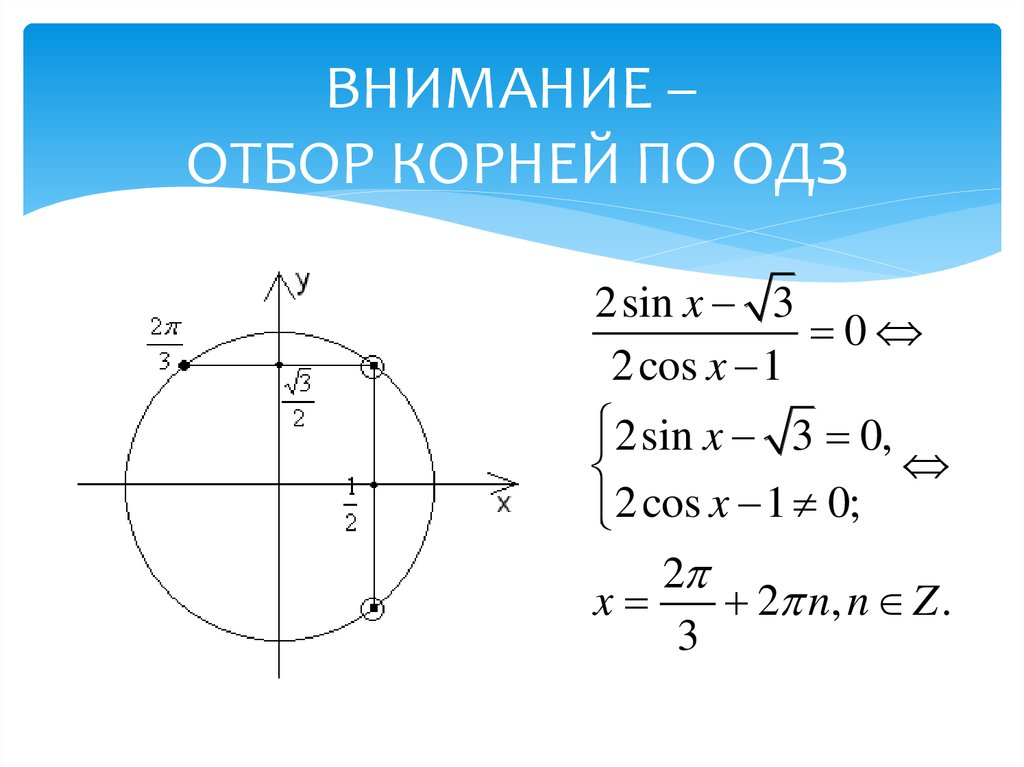
17. ВНИМАНИЕ – ОТБОР КОРНЕЙ ПО ОДЗ
2sin x 30
2 cos x 1
2sin x 3 0,
2 cos x 1 0;
2
x
2 n, n Z .
3
18. Методические рекомендации по организации итогового повторения тригонометрических уравнений
Запись решений простейших тригонометрическихуравнений
Методы (приемы) решений тригонометрических
уравнений
Приемы отбора корней уравнения из промежутка:
основной – с использованием тригонометрической
окружности
19. Внимание – простые уравнения!
2x
2
x
,
x 1,
2
log 7 x 2 log 7 x
x 2.
x 2 0;
0 баллов!
log 7 x 2 log 7 x
x 2 x2
2
log 7 x 2 log 7 x 2
ОДЗ : x 2 0 x 0.
x 2 x2
Ответ : 1; 2.
Ответ : 1; 2.
log 7 x 2 log 7 x 2
log 7 x 2 log 7 x 2
ОДЗ : x 0.
2
x 2 x2
Ответ : 1; 2.
x 2 0,
ОДЗ : 2
x 2.
x 0;
x 2 x2
Ответ : 1; 2.
20. Какое решение правильное?
x 9lg x( x 9) lg
0
x
х 9
lg х х 9
0
х
lg x( x 9) lg
lg( x 9) lg 1
lg x( x 9) lg
( x 9) 1
x ( x 9)
2
2
Ответ: -10, -8.
Ответ: -8.
x
x 9
x
x 9
Ответ: -10, -8, 0.
lg x lg( x 9) lg( x 9) lg x 0
2 lg( x 9) 0
x 9
x
21. 15. Решение неравенства
9 log12 x 2 3 x 4 10 log12x 1
9
x 4
x 2 3 x 4 0,
9
9
x
1
2
10;
log12 x 3 x 4 log12
x 4
x 1 x 4 0,
9
10
x 1 x 4
10;
log12
9
x
1
x 1 x 4 0,
10
log
x
4
10;
12
x 1 x 4 0,
10 log12 x 4 10;
x 1 x 4 0,
x 4 12.
Ответ : 8; 1 4;16 .
9log12 x 3x 4 10 log12
2
x 1
9
x 4
x 3x 4 0,
9log12 x 1 9log12 x 4 10 9log12 x 1 log12 x 4 ;
x 1 x 4 0,
10log12 x 4 10;
2
x 1 x 4 0,
x 4 12.
Ответ : ; 1 4;16 .
Главные вопросы:
Можно ли выполнить преобразование?
При каких условиях?
22. 15. Решение неравенства
x2 1
2 log 5 x 2 log 5
log
8
x
5
5
x
1 x
Зачем?
2 log 7
x 2 0;
x
ОДЗ :
0;
1
x
2 1
8 x x 5 0.
2 1
log
2
x
1
x
log
8
x
5
x
1
7
2
7
;
x 2 log 7
log
8
x
5
x
7
x
1 x
0 x 1,
1
2
5 x 1 2 x 2 1 0;
10 x3 2 x 2 5 x 1 0;
2 x 1 x 8 x 5;
x
0 x 1,
0 x 1.
0 x 1,
1 2
Ответ : 0;
;1 .
5 2
23. Поговорим про ОДЗ!
Уравнением с одним неизвестным называется равенствоf1 x f 2 x
где f1 x и f 2 x функции, рассматриваемые в общей части их
областей определения.
x 2 x 4
В структуру этого уравнения входят функция арифметического
квадратного корня (левая часть) и линейная функция (правая часть).
Так как линейная функция определена для любых х, а арифметический
квадратный корень существует при неотрицательных значениях
подкоренного выражения, то ОДЗ данного уравнения: x 2 0
х 2 x 4
2
х 2 9 х 14 0
х 2, х 7
Оба корня удовлетворяют ОДЗ
x 4 0,
x 4 0,
х 2,
2
х 4 х 2;
х 7.
Ответ : 7.
24. Поговорим про ОДЗ!
Пример «типичного» решения3x 5 4 x 1
3 x 5 0,
ОДЗ :
4 x 0.
( 3 x 5 4 x ) 2 12
3 х 2 17 х 20 х 1
4 х 2 19 х 21 0
х 3, х 1, 75
Оба корня удовлетворяют ОДЗ
Ответ : 3;1, 75.
Пример правильного решения
3x 5 0;
4 x 0;
3х 5 4 x;
3x 5 4 x
2
x 4,
х 2, 25,
x 1 0,
3 x 2 17 x 20
4 x 0;
3х 5 4 x;
2
1 ; 3x 5 4 x
2
x 4;
х 2, 25; х 3.
x 3;
1
x2 1, 75,
x 1 ;
2
2
12 ;
x 4,
х 2, 25,
2
4 х 19 х 21 0;
Ответ :3.
25. Равносильные переходы
log 3 х 2 х log 3 3 х 2log 3 х 2 х log 3 3 х 2
х 2 х 3 х 2,
3 х 2 0.
х 2 х 3 х 2,
3 х 2 0.
Одно из выражений больше нуля
Меньшее из выражений больше нуля
log 3 х 2 х log 3 3 х 2
log 0,3 х 2 х log 0,3 3 х 2
х 2 х 3х 2,
2
х х 0.
х 2 х 3х 2,
2
х х 0.
Меньшее из выражений больше нуля Меньшее из выражений больше нуля
26. Равносильные переходы
log 3 х log 3 х 8 log 3 х 3х 0,
х 8 0,
x
1
log 3
log 3
;
x 8
х 3
х 0,
1
x
;
х 3
x 8
log 4
3 x
2
log 0,25 х 3 log 1 х 7
x 7
4
log 1
x 7
2
log 1 х 3 log 1 х 7
3 x
4
4
4
х 0,
x 4, x 2.
x 2;
x 7
0,
x 7 0,
3 x
х 3 0,
х 3 0,
2
( x 7) ( х 3)
2
log 1
log 1 (7 x) log 1 х 7 ;
log 1 х 7 ;
4
4
3 x
4
4
x 7 0,
3 х 7,
х
3
0,
x 3;6 .
х
7
х
6
0
;
2
7
x
х
7
;
Ответ : 3;6 .
27. Какое решение правильное?
log 3 x 2 х 2 1 log3x 2 х 2 0;
ОДЗ: x 1
0.
x 2
х ; 1 2;
x 2 х 2 0;
ОДЗ: x 1
0.
x 2
х ; 1 2;
log3 х 2 log3 x 1 1 log3 x 1 log3 x 2
2log3 х 2 1
1
log 3 х 2
2
x 2 3
x 2 3
х 1
х 2
х 2 х 1 1
2
log3
х 1
2
х 2 х 1
х 1
2
х 2 3
С учетом ОДЗ имеем: х ; 1 2; 2 3
3
х 2 3; 2 3
С учетом ОДЗ имеем:
х 2; 2 3
Как лучше оформить правильное решение?
28. Пример оформления
8x
17. Решите неравенство log 2
10
0.
log 2 16 x
Решение
10
0,
log 2 16 log 2 x
10
3 log 2 x
0.
4 log 2 x
10
0.
Пусть log 2 x t , тогда 3 t
4 t
12 3t 4t t 2 10
t2 t 2
0,
0.
4 t
4 t
t2 t 2
Рассмотрим f t
. Найдем t, для которых f t 0 .
4 t
1) D f : t 4 .
2) f t 0 , если t 2 t 2 0 , т.е. t 2 , t 1 .
log 2 8 log 2 x
3) Промежутки знакопостоянства функции:
–
+
–4
–
+
–2
1
t
29.
t 4 , – 2 t 1 .x 0,
log 2 x 4 , следовательно,
1
x
.
16
1
– 2 log 2 x 1 , следовательно, t 2 .
4
1
1
Ответ. x 0; ;2 .
16 4
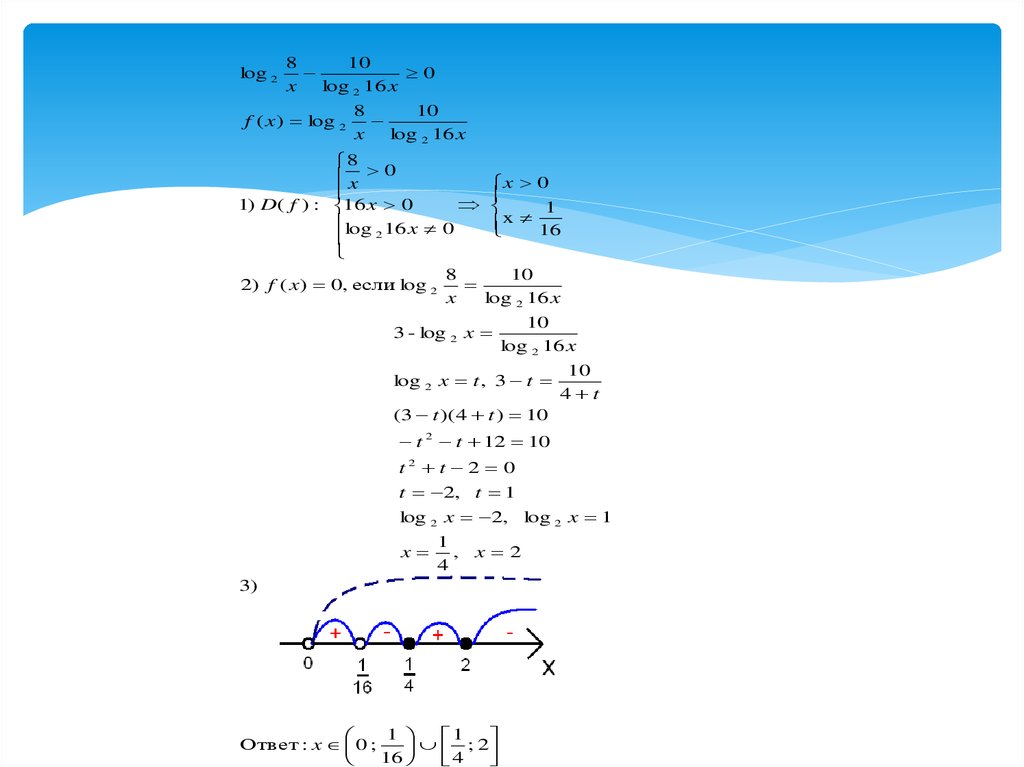
30.
log 28
10
0
x
log 2 16 x
f ( x ) log 2
8
10
x
log 2 16 x
8
x 0
x 0
1) D ( f ) : 16 x 0
1
x
log 16 x 0
16
2
8
10
2) f ( x ) 0, если log 2
x
log 2 16 x
3 - log 2 x
10
log 2 16 x
log 2 x t , 3 t
10
4 t
(3 t )( 4 t ) 10
t 2 t 12 10
t2 t 2 0
t 2, t 1
log 2 x 2, log 2 x 1
x
1
,
4
x 2
3)
1
1
Ответ : x 0 ;
; 2
16
4
31. Пример оценивания решения неравенства
Оценка эксперта – 0 баллов.32. 0 баллов!
33. Пример неправильного решения неравенства
34. Пример неправильного решения
35. Метод интервалов – полюбить!
4х2 х 4
2 х 2 2 х 1
0,5
х
0, 2 5 1
0
1)0, 2 5 1 0, х 1.
х
2)4
х2 х 4
0,5
2 х 2 2 х 1
3)
3 3
Ответ : ; 1; .
2 2
3
0, х .
2
36. Методические рекомендации по организации повторения
Вспомнить алгоритмы решений неравенств, эвристическиепредписания (квадратное неравенство – парабола;
дробно-рациональное неравенство – метод интервалов;
логарифмическое неравенство – система: первая строчка –
ОДЗ, вторая – монотонность; и т.д.)
При решении неравенства методом интервалов четко
выделить функцию, о которой идет речь.
Решать одно неравенство разными методами.
Показать оформление решения неравенства разными
методами в сравнении.
Научить проверять граничные точки – подстановкой.
37. 17. «Экономическая» задача
38. Аннуитетные платежи
В июле 2020 года планируется взять кредит в банке на некоторую сумму.Условия его возврата таковы:
– каждый январь долг увеличивается на 25% по сравнению с концом
предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним
платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит
будет полностью погашен тремя равными платежами (то есть за три года)
и общая сумма выплат после полного погашения кредита на 65 500
рублей больше суммы, взятой в кредит?
39. Задача 8 класса
40. Обратная задача
41. Дифференцированный платеж
42.
43.
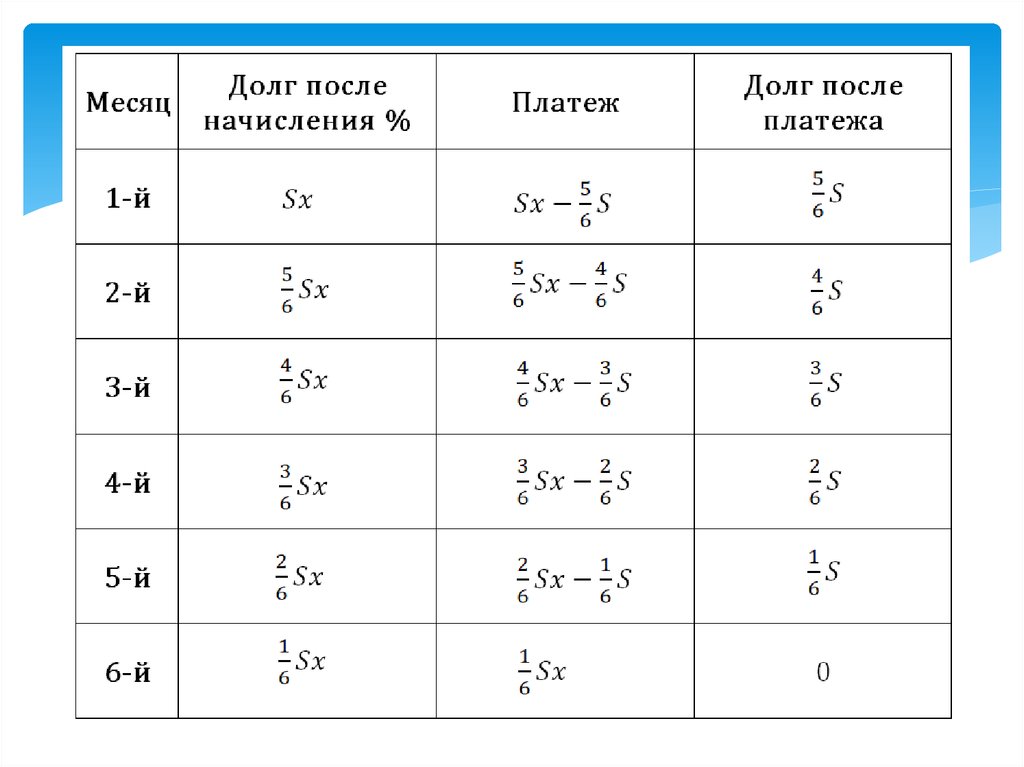
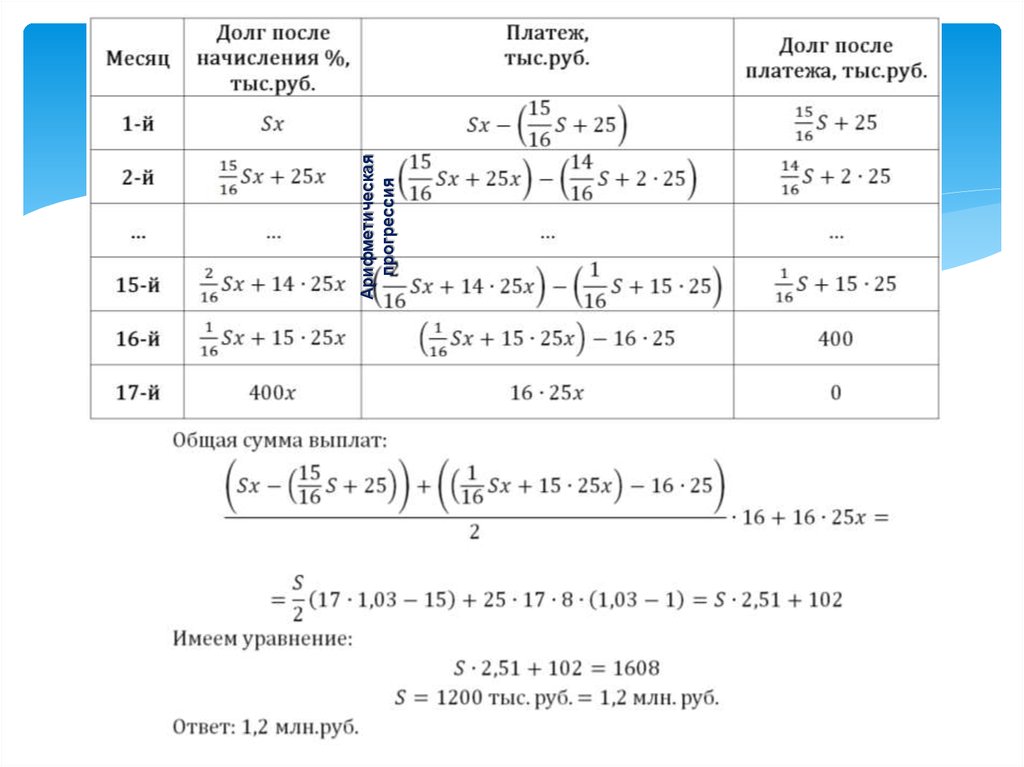
44. Дифференцированный платеж с «подвохом»
45.
46.
Арифметическаяпрогрессия
47. Долг – в таблице
48. Математическая модель – квадратичная функция
49. Математическая модель – квадратичная функция
50. Задачи на оптимизацию
51. 14. Стереометрическая задача
52. Учимся оформлять!
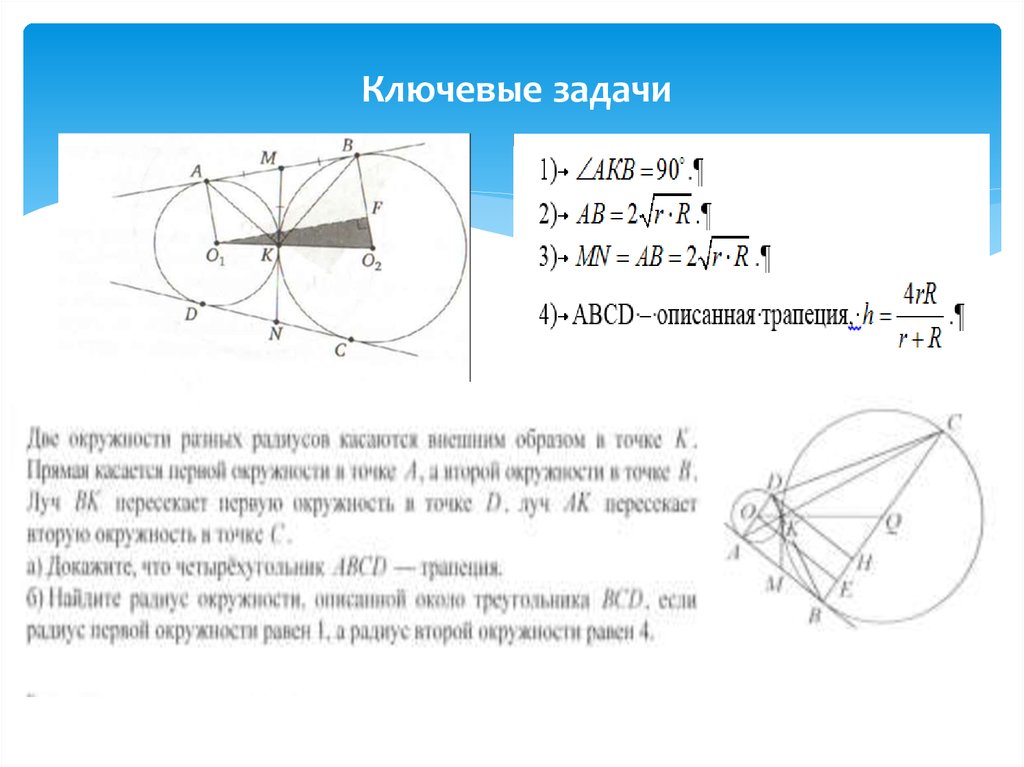
или53. 16. Планиметрическая задача
54. Ключевые задачи
55. 18. Задачи с параметром
56. Учить методам
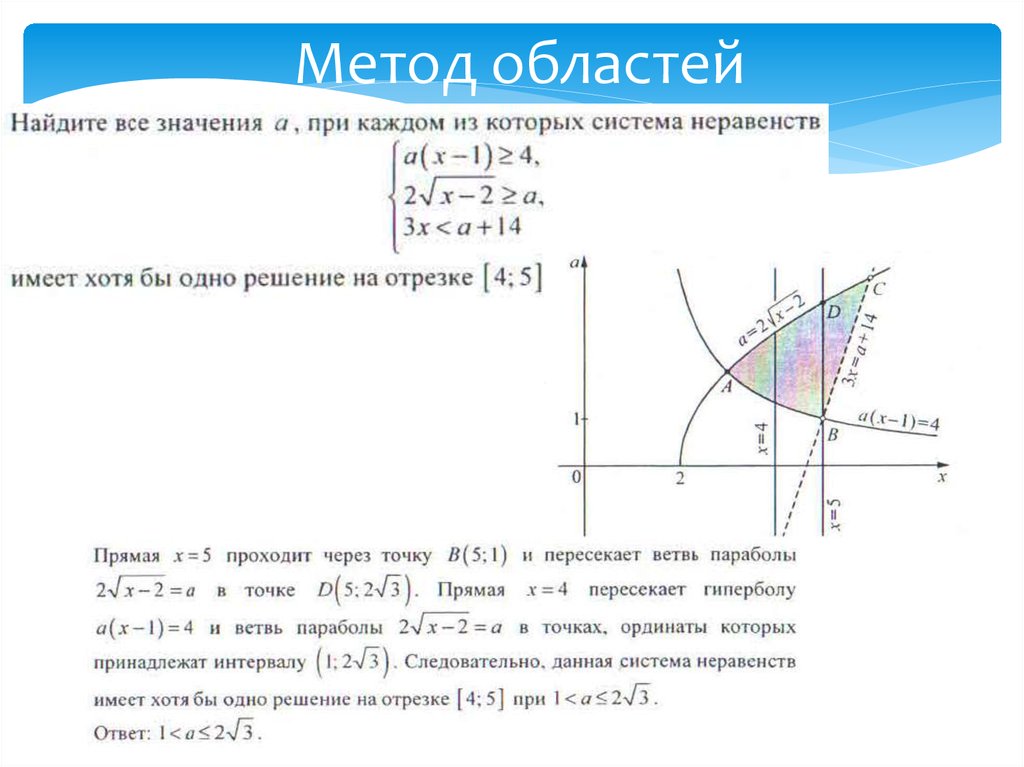
Графический методМетод областей
Инвариантность






















































 mathematics
mathematics








