ЕГЭ по математике 2012. (Часть 2)

1. ЕГЭ ПО МАТЕМАТИКЕ 2012 (часть 2)

Лосева
Екатерина Анатольевна

2.

1) Дано уравнение
3
cos(
2 x) cos x
2
а) Решите уравнение
5
;
4
б) Укажите корни уравнения, принадлежащие отрезку 2
Решение:
а) Используем формулы приведения для преобразования левой части уравнения:
3
cos(
2 x ) sin x (IV четверть, название меняется)
2
Новое уравнение: sin 2 x cos x
2 sin x cos x cos x 0
cos x( 2 sin x 1) 0
Данное уравнение равносильно совокупности:
cos
x
0
x
k , k Z
2
sin x 1 x ( 1) n n, n Z
2
6
Значит, ответ на первый вопрос:
x
2
( 1) n
k , k Z ;
6
n, n Z

3.

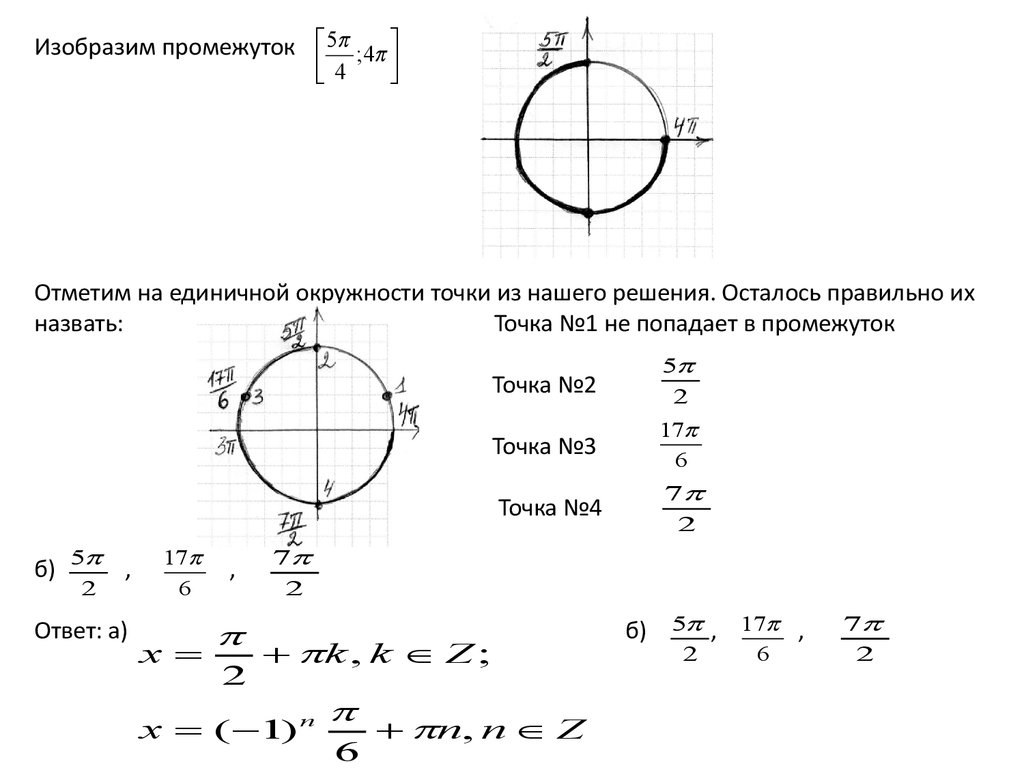
Изобразим промежуток 5 ;4
4
Отметим на единичной окружности точки из нашего решения. Осталось правильно их
назвать:
Точка №1 не попадает в промежуток
б) 5 ,
2
Ответ: а)
17
6
x
,
2
Точка №2
5
2
Точка №3
17
6
Точка №4
7
2
7
2
k , k Z ;
x ( 1) n
6
n, n Z
б) 5 , 17 ,
2
6
7
2

4.

2) а) Решите уравнение sin x (cos
x
x
x
x
sin )(cos sin ) 0
2
2
2
2
5
б) Укажите корни этого уравнения, принадлежащие промежутку ; 2
Решение: а) преобразуем уравнение:
x
x
sin 2 0
2
2
sin x cos x 0 -однородное уравнение первой степени
sin x cos 2
sin x cos x 0 : cos x 0
tgx 1
x
б) Составим неравенство
4
k , k Z
5
k
:
4
2
1
5
1
1
k
4
2
4
5
11
k
' т.к.k Z , k 2
4
4

5.

Значит на данном отрезке единственный корень
x
Ответ: а)
б)
x
7
4
4
7
2
4
4
k , k Z
3) а) Решите уравнение
sin 2 x 2 3 cos 2 x 4 sin x 4 3 cos x 0
5
б) Укажите корни, принадлежащие промежутку ;
2
Решение: Преобразуем левую часть уравнения:
2 sin x cos x 2 3 cos 2 x 4 sin x 4 3 cos x 0
Коэффициент
2 3 указывает на возможность группировки:
(2 sin x cos x 4 sin x) ( 2 3 cos 2 x 4 3 cos x) 0
2 sin x(cos x 2) 2 3 cos x(cos x 2) 0
(cos x 2)(2 sin x 2 3 cos x) 0

6.

Это уравнение равносильно совокупности:
cos x 2 нет решений
2 sin x 2 3 cos x 0
ное уравнение II степени.
2 sin x 2 3 cos x 0 : 2 cos x 0
tgx 3 0
tgx 3
x k , k Z
3
-это ответ на первый вопрос
б)
4 7
;
3
3
Ответ: а)
б)
x
k , k Z
3
4 7
;
3
3
однород-

7.

4) Сложный дискриминант и отбор корней.
Решите уравнение: 6 sin 2 x (4 3 3 ) cos x 2
3 (1 3 ) 0
и найдите все его корни из промежутка 3 ;3
2
Решение: а) преобразуем левую часть уравнения:
6(1 cos 2 x) (4 3 3 ) cos x 2 3 (1 3 ) 0
6 6 cos 2 x (4 3 3 ) cos x 2 3 (1 3 ) 0
6 cos 2 x (4 3 3 ) cos x 2 3 6 6 0
6 cos 2 x (4 3 3 ) cos x 2 3 0
cos x t
6t 2 (4 3 3 )t 2 3 0
D (4 3 3 ) 2 4 6 2 3
4 2 2 4 3 3 (3 3 ) 2 4 6 2 3
4 2 24 3 (3 3 ) 2 48 3 4 2 24 3 (3 3 ) 2 (4 3 3 ) 2

8.

4 3 3 (4 3 3 ) 2
4 3 3 (4 3 3 )
t1
12
12
4 3 3 (4 3 3 ) 2
4 3 3 (4 3 3 )
t2
12
12
8
2
t1
12
3
6 3
3
t2
12
2
2
2
cos
x
x
arccos(
) 2 k , k Z
Выполним обратную замену:
3
3
3
cos
x
x
2 n, n Z
2
6
Для того, чтобы ответить на второй вопрос, надо знать как расположено
решение уравнения на единичной окружности.
б)
11 13
2
;
;3 arccos
6
6
3

9.

С2. Основанием прямой призмы ABCA1B1C1 является равнобедренный треугольник
ABC, AB=AC=5, BC=8. Высота призмы 3. Найдите угол между прямой A1B и плоскостью
BCC1.
Решение: Нужно найти угол между прямой и плоскостью, а значит, угол между прямой
и ее проекцией на эту плоскость.
1) Опустим перпендикуляр А1М на плоскость ВСС1.
A1 M C1 B1
A1M CC1 (так как призма прямая), а значит
A1M плоскостиBCC1
Тогда прямая BM будет проекцией A1B на плоскость BCC1
2)Теперь мы знаем, что искомый угол равен углу A1BM.
Сделаем вынесенный чертеж.
A1 BM
A M ( BCC ))
1
прямоугольный ( 1
A1 BM надо найти две любые
а значит для поиска
стороны.

10.

3) Найдем BM . В BB1M (прямоугольном)
( A1M -медиана) , BB1 3
Значит,
BM B1M 2 BB12 16 9 5
Найдем A1M из прямоугольного
A1MB1
A1M A1 B12 B1M 2 25 16 3
4)
A1M 3
tg A1 BM
0,6
MB 5
A1 BM arctg 0,6
Ответ : arctg 0,6
BM - гипотенуза. BM 1 4

11.

С2. В правильной четырехугольной призме ADCDA1 B1C1 D1 сторона основания равна
2
M ребра
M
AA1 расстояние от точки
, а высота
равна 1.
середина
.Найдите
до плоскости DA1C1 .
Решение: 1) Удобно ввести в рассмотрение треугольную пирамиду MDA1C1 .
Ее высота из вершины M на плоскость DA1C1 и даст
нам искомое расстояние.
2) Рассмотрим объем этой пирамиды двумя способами:
а)
1
V S DA C
3 1 1
б) «Перевернем» пирамиду, взяв в качестве вершины
C1
1
1 1
1 1
1
1
S MA1D C1 D1 ( AD MA) C1 D1 ( 2 ) 2
3
3 2
3 2
2
6
3) Эти два объема , естественно, равны, значит
V
1
1
S DA1C1 ,
3
6
-искомое расстояние. Остается найти S DA C
1 1

12.

4) В DA1C1 (равнобедренном, так как A1 D1 C1 D ) проведем высоту
DH
DA12 A1 H 2
DA12 AA12 AD 2 12 2 2 3
Значит,
Тогда:
5)
Ответ:
( 2 )2 ( 2 )2
A1C
A1 H
1
2
2
DH 3 1 2
S DA1C1
1
1
DH A1C1
2 2
2
2
1 1
1 1
3
1
: ( S DA1C1 ) : ( 2 )
6 3
6 3
6 2 2 2
1
2 2
2
4
2
4
2
DH