Решение физических задач ЕГЭ по математике

1.

МОУ «СОШ № 34 с углубленным изучением
художественно-эстетических предметов»
Н.И. Хренникова,
учитель математики
Решение физических
задач ЕГЭ по
математике.
Саратов
2014

2. Задания с наибольшим количеством аналогов

3.

Прототип: 28009
Задание B12 (№ 28643)
Два тела массой
кг каждое движутся с одинаковой скоростью
м/с
под углом
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно
неупругом соударении определяется выражением
. Под каким
наименьшим углом
(в градусах) должны двигаться тела, чтобы в результате
соударения выделилось не менее 108 джоулей?
Задание B12 (№ 28613)
Прототип: 28006
Трактор тащит сани с силой
кН, направленной под острым углом
к
горизонту. Работа трактора (в килоджоулях) на участке длиной
м
вычисляется по формуле
. При каком максимальном
угле
(в градусах) совершeнная работа будет не менее 2800 кДж?
Задание B12 (№ 28053)
Прототип: 27956
Зависимость объeма спроса q (единиц в месяц) на продукцию предприятиямонополиста от цены p (тыс. руб.) задаeтся формулой
. Выручка
предприятия за месяц r (в тыс. руб.) вычисляется по формуле
. Определите
наибольшую цену p, при которой месячная выручка
составит не менее
360 тыс. руб. Ответ приведите в тыс. руб.

4. Задания с наименьшим количеством аналогов

5.

Задание B12 (№ 41991)
Прототип: 27973
Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением
электроприбора по закону Ома:
, где U — напряжение в вольтах, R — сопротивление
электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила
тока превышает 1 А. Определите, какое минимальное сопротивление должно быть у
электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ
выразите в омах.
Прототип: 27959
Задание B12 (№ 28083)
В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его
открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в
метрах, меняется по закону
, гдеt — время в секундах, прошедшее с
момента открытия крана,
м — начальная высота столба воды,
—
отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения
(считайте
м/с ). Через сколько секунд после открытия крана в баке останется четверть
первоначального объeма воды?
Задание B12 (№ 28393)
Прототип: 27987
Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути
длиной l км с постоянным ускорением a км/ч , вычисляется по формуле
. Определите,
с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 0,4 километра от
старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не
меньше 12500 км/ч . Ответ выразите в км/ч.

6. Шаги решения В12

Решение задач В12 условно можно разделить на несколько шагов:
а) анализ условия и вычленение формулы, описывающей заданную
ситуацию, а также значений параметров, констант или начальных условий,
которые необходимо подставить в эту формулу;
б) математическая интерпретация задачи — сведение её к уравнению или
неравенству и его решение;
в) анализ полученного решения.
Задания В12 отличаются от других тем, что очень высок процент тех, кто
даже не приступал к решению.
Основные проблемы — трудности с арифметикой, логические ошибки,
невнимательное чтение условия.

7. Задачи, решение которых сводятся к стандартным уравнениям и неравенствам

линейному уравнению или неравенству
степенному уравнению или неравенству
показательному уравнению или неравенству
логарифмическому уравнению и неравенству
тригонометрическому уравнению или неравенству

8. Задание B12 (№ 28017)

При температуре 0oС рельс имеет длину lo= 20 м. При
возрастании температуры происходит тепловое
расширение рельса, и его длина, выраженная в метрах,
меняется по закону l(to) = l0 ( 1+α·to), где α = 1,2·10-5(oC)-1
– коэффициент теплового расширения, to - температура
(в градусах Цельсия). При какой температуре рельс
удлинится на 9 мм? Ответ выразите в градусах
Цельсия.

9.

Данные:
l0 2 104 мм; 1,2 10 5 (0C ) 1.
Функция:
Найти:
l (t 0 ) l0 (1 t 0 )
t 0 при l (t 0 ) 20009 мм
Получаем уравнение:
l (t 0 ) 20000 2 104 1,2 10 5 t 0
20009 0,24 t 0 20000
9 0,24 t 0
9
900
0,24 24
75
37,50 С
2
t0
Ответ: 37,5.

10. Задание B12 (№ 28027)

Некоторая компания продает свою продукцию по цене
p = 600 руб.
за единицу, переменные затраты на производство одной единицы
продукции составляют ν = 400 руб., постоянные расходы предприятия
f = 600000 руб. в месяц. Месячная операционная прибыль (в рублях)
вычисляется по формуле π(q) = q( p - ν)- f . Определите наименьший
месячный объём производства q (единиц продукции), при котором
месячная операционная прибыль предприятия будет не меньше
500000 руб.

11.

Данные: p 600 руб.,
400 руб.
f 600000 руб.
Функция: (q ) q ( p ) f
Найти: qнаим. при (q ) 500000.
Решаем неравенство:
200q 600000 500000
200q 1100000
q 5500
qнаим. 5500
Ответ: 5500.

12.

Задание B12 (№ 28027)
Для обогрева помещения, температура в котором Тп = 20°С, через радиатор
пропускают горячую воду температурой Т= 60°С. Через радиатор проходит m= 0,3
кг/с воды. Проходя по радиатору расстояние х = 84 м, вода охлаждается до
температуры T(°С), причём
где с = 4200 - теплоёмкость воды, γ= 21 - коэффициент теплообмена,
а α = 0,7 — постоянная. До какой температуры (в градусах Цельсия) охладится вода?

13.

Данные:
Тп = 20°С
m= 0,3 кг/с
х = 84 м
α = 0,7
с = 4200
Функция:
Найти: Т-?°С
Получаем уравнение:
Ответ: 30

14.

Задание B12 (№ 28027)
Находящийся в воде водолазный колокол, содержащий ν= 4 моля воздуха
при давлении р1 = 1,2 атмосферы, медленно опускают на дно водоёма. При
этом происходит изотермическое сжатие воздуха. Работа (в джоулях),
совершаемая водой при сжатии воздуха, определяется выражением
где α = 5,75 — постоянная, Т = 300 К—температура воздуха, P1 (атм) начальное давление, а р2 (атм) — конечное давление воздуха в колоколе.
До какого наибольшего давления р2 (в атм) можно сжать воздух в
колоколе, если при сжатии воздуха совершается работа не более чем
20 700 Дж?

15.

Данные:
α = 5,75
ν= 4
Т = 300
р1 = 1,2
Функция:
, при
Найти:
Получаем неравенство:
Ответ: 9,6

16.

,
Задание B12 (№ 28006)
Трактор тащит сани с силой F = 80 кН, направленной под острым углом а к
горизонту. Работа трактора, выраженная в килоджоулях, на участке длиной S = 50 м
равна
А = FS cos α.
При каком максимальном угле а (в градусах) совершённая работа будет
не менее 2000 кДж?

17.

Данные:
S = 50
F =80
Функция:
Найти:
А = FS cos α.
а (в градусах), при
А ≥ 2000
Получаем неравенство:
80•50• cos α ≥ 2000
cos α ≥
0°< α≤ 60
°
Ответ: 60

18.

Задание B12 (№ 27991)
В ходе распада радиоактивного изотопа его масса
уменьшается по закону
m(t) = m0.2-t/T,
где m0 — начальная масса изотопа, t — время, прошедшее от начала распада,
Т — период полураспада в минутах. В лаборатории получили вещество,
содержащее m0 = 40 мг изотопа азота-13, период полураспада которого
Т = 10 мин. В течение скольких минут масса изотопа азота-13 будет
не меньше 10 мг?

19.

Данные:
Т = 10 мин
m0 = 40 мг
Функция:
Найти:
m(t) = m0.2-t/T,
t , если
m(t) ≥ 10
Получаем неравенство:
40 *2 -t/10 ≥ 10 ,
2 -t/10 ≥ 2-2 ,
t ≤ 20
Ответ: 20

20. Задачи, решения которых сводятся к квадратным уравнениям и неравенствам.

21.

Задание B12 (№ 28135)
Мотоциклист, движущийся по городу со
скоростью v0 = 57 км/ч, выезжает из него и
сразу после выезда начинает разгоняться с
постоянным ускорением a = 12 км/ч2.
Расстояние от мотоциклиста до города,
измеряемое в километрах, определяется
2
at
выражением S = v t
0
2
Определите наибольшее время, в течение
которого мотоциклист будет находиться в зоне
функционирования сотовой связи, если
оператор гарантирует покрытие на расстоянии
не далее чем в 30 км от города. Ответ
выразите в минутах.

22.

Данные: v0 57,
a 12.
at 2 S 57t 6t 2
Функция: S v0t
2
Найти: tнаиб. 0 при S 30.
Решаем неравенство:
2
30 57t 6t 2
D
19
4 10 2
2
6t 57t 30 0, |: 3 361 80 441 212.
t1 10, t 2 0,5
2
2t 19t 10 0
10 t 0,5
Ответ:
30.

23.

Задание B12 (№ 28125)
Для сматывания кабеля на заводе используют лебёдку,
которая равноускоренно наматывает кабель на катушку.
Угол, на который поворачивается катушка, изменяется со
βt2
временем по закону φ = ωt
, где t — время в
2
минутах, ω = 750/мин — начальная
угловая скорость вращения катушки,
а β = 100/мин2 — угловое ускорение, с которым
наматывается кабель. Рабочий должен
проверить ход его намотки не позже того момента,
когда угол намотки φ достигнет
Определите время после начала
22500.
работы лебёдки, не позже которого
рабочий должен проверить её работу.
Ответ выразите в минутах.
Лебёдка — механизм, тяговое
усилие которого передается
посредством каната, цепи, троса
или иного гибкого элемента от
приводного барабана.

24.

Данные:
75,
10.
Функция: t
Найти:
tнаиб.
t 2
.
2
0 при 2250.
Решаем неравенство:
D 152 4 450
3252 4 9 25 2
3252 (1 4 2)
325232 452.
t1 30, t2 15 tнаиб.
(больший корень)
Ответ: 15.

25.

Задание B12 (№ 28165)
Деталью некоторого прибора является вращающаяся
катушка. Она состоит из трёх однородных соосных
цилиндров: центрального массой m = 8 кг и радиуса R =
5 см, и двух боковых с массами M = 2 кг и с радиусами
R + h. При этом момент инерции катушки относительно
оси вращения, выражаемый в кг· см2 , даётся формулой
(m+2M)R2
I =
+ M(2Rh
. + h2).
2
При каком максимальном значении h момент инерции
катушки не превышает предельного значения 1900 кг· см2
? Ответ выразите в сантиметрах.

26.

Данные:
m 8,
M 2,
R 5.
Функция:
(m 2M ) R 2
I
M (2 Rh h 2 ).
2
Найти:
hmax 0 при I 1900.
Решаем неравенство:
2
D
10
4 875
2
1900 2h 20h 150.
100 3500
2
2
300
60
.
2h 20h 1750 0, |: 2
h 2 10h 875 0.
h1 35, h2 25
Ответ: 25.

27.

Задание B12 (№ 28053)
Зависимость объёма спроса q (тыс. руб.) на
продукцию предприятия-монополиста от цены p
(тыс. руб.) задаётся формулой q = 130 - 10p .
Выручка предприятия за месяц
r (в тыс. руб.)
вычисляется по формуле r(p) = q · p. Определите
наибольшую цену p, при которой месячная
выручка составит не менее 360 тыс. руб.
Ответ приведите в тыс. руб.

28.

Данные: q 130 10 p, r ( p) q p
Функция:
Найти:
r ( p ) (130 10 p ) p
pнаиб. при r ( p) 360.
Получаем неравенство:
10 p 2 130 p 360,
p 2 13 p 36 0
4 p 9
Ответ: 9.

29.

Задание B12 (№ 28105)
Камнеметательная машина выстреливает камни под
некоторым острым углом к горизонту. Траектория
полёта камня описывается формулой y = ax2 + bx ,
-1
7
-1
где a
м ,b
— постоянные параметры,
60
6
x (м) — смещение камня по горизонтали, y (м) —
высота камня над землёй. На каком наибольшем
расстоянии (в метрах) от
крепостной стены высотой 9 м нужно расположить
машину, чтобы камни пролетали над стеной на
высоте не менее 1 метра?

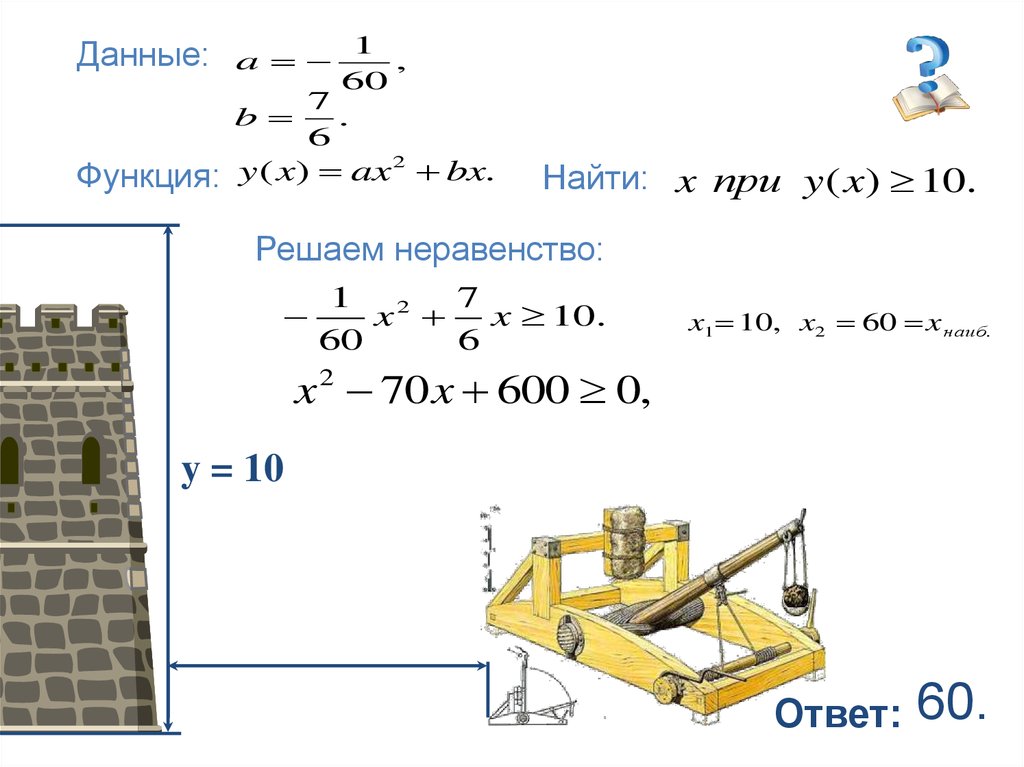
30.

Данные:
1
,
60
7
b
.
6
a
2
y
(
x
)
ax
bx.
Функция:
Найти: x при y ( x) 10.
Решаем неравенство:
1
7
x2
x 10.
60
6
x1 10, x2 60 x наиб.
x 2 70 x 600 0,
y = 10
Ответ:
60.

31.

Задание B12 (№ 28091)
В боковой стенке высокого цилиндрического бака у самого
дна закреплён кран. После его открытия вода начинает
вытекать из бака, при этом высота столба воды в нём,
выраженная в метрах, меняется по закону
H(t) = H0 + bt + at2 , где Н0 = 2 м — начальный уровень воды,
1
-2
2
a
м/мин , b
м/мин, t — время в минутах,
50
5
прошедшее с момента открытия
крана. В течение какого времени
вода будет вытекать из бака? H0
Ответ приведите в минутах.

32.

Данные:
H 0 2 м,
1
a
,
50
2
b .
5
2
Н
(
t
)
H
bt
at
Функция:
0
Найти: t при H (t ) 0.
Решаем уравнение:
2
1 2
2 t
t 0,
5
50
100 20t t 2 0,
t 10
2
0 t 10.
Ответ: 10.

33.

Задание B12 (№ 28081)
В боковой стенке высокого цилиндрического бака у самого
дна закреплён кран. После его открытия вода начинает
вытекать из бака, при этом высота столба воды в нём,
выраженная в метрах, меняется по закону
g 2 2 , где t — время в секундах,
H (t ) = H0 — 2gH 0 kt k t
2
прошедшее с момента открытия крана, k = 1 —
200
отношение площадей поперечных сечений крана и бака,
Н0 = 5 м — начальная высота столба воды, а g — ускорение
свободного падения (считайте g = 10 м/с2).
Через
сколько секунд после открытия крана в баке останется
четверть первоначального объёма воды?

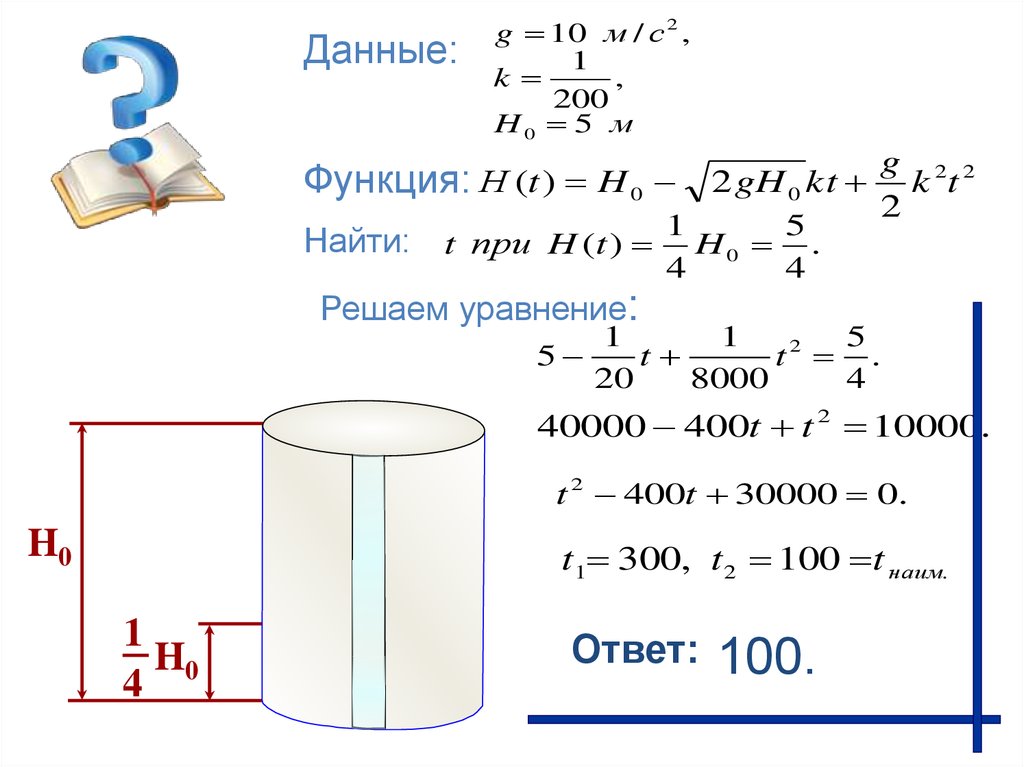
34.

Данные:
g 10 м / с 2 ,
1
k
,
200
H0 5 м
Функция: Н (t ) H 0
Найти: t при H (t )
2 gH 0 kt
1
5
H0 .
4
4
g 2 2
k t
2
Решаем уравнение:
5
1
1
5
t
t2 .
20
8000
4
40000 400t t 2 10000.
t 2 400t 30000 0.
H0
t 1 300, t2 100 t наим.
1
H0
4
Ответ:
100.

35.

Задание B12 (№ 28115)
Зависимость температуры (в градусах Кельвина) от
времени для нагревательного элемента некоторого
прибора была получена экспериментально и на
исследуемом интервале температур определяется
выражением T(t) = T0 + bt + at2 , где t — время в
минутах, T0 = 1450 К, a = - 12,5 К/мин2 , b = 175 К/мин.
Известно, что при температуре нагревателя свыше
1750 К прибор может испортиться, поэтому его нужно
отключать. Определите, через какое наибольшее
время после начала работы нужно отключать
прибор. Ответ выразите в минутах.
Пирометр — прибор для беcконтактного измерения температуры тел.

36.

T0 1450,
a 12,5,
b 175.
Данные:
Функция:
2
T (t ) T0 bt at T
(t ) 1450 175t 12,5t 2
Найти: t наиб. 0 при T (t ) 1750.
Схематичный график:
1750 1450 175t 12,5t 2
12,5t 2 175t 300 0, | 2
y
1750
25t 2 350t 600 0, |: 25
y = T(t)
t 2 14t 24 0,
t 2, t 12
Ответ: 2.
1450
0
tнаиб.
Необходимо
отключить
t

37. Задачи, в которых необходимо найти длину промежутка.

38.

Задание B12 (№ 28039)
1,2 с
1,1 с
После дождя уровень воды в
колодце может повыситься.
Мальчик измеряет время t
падения небольших камешков
в колодец и рассчитывает
расстояние до воды по
формуле h = 5t2, где
h — расстояние в метрах,
t — время падения в секундах.
До дождя время падения
камешков составляло 1,2 с.
На сколько должен подняться
уровень воды после дождя,
чтобы измеряемое время
изменилось на 0,1 с?

39.

Данные: tдо 1,2 с, t 0,1, tизм. 1,1 с.
Функция: h 5t 2
Найти:
h h(1,2) h(1,1)
Решение:
h 5 1,2 5 1,1
2
2
5 (1,2 1,1 )
5 (1,2 1,1) (1,2 1,1)
5 0,1 2,3 1,15( м)
2
2
Ответ: 1,15.

40.

Задание B12 (№ 28059)
Высота над землёй подброшенного вверх мяча меняется по
закону h(t) = 1,4 + 9t - 5t2 , где h — высота в метрах, t —
время в секундах, прошедшее с момента броска. Сколько
секунд мяч будет находиться на высоте не менее 3 метров?

41.

Данные: h(t ) 3
Функция: h(t ) 5t 2 9t 1,4
Найти: t t2 t1
Получаем неравенство: 5t 2 9t 1,6 0,
5t 2 9t 1,4 3.
0,2 t 1,6
t 1,6 0,2 1,4
D 81 32 49,
t1 0,2, t1 1,6.
Ответ: 1,4

42. Задачи, в которых присутствуют несколько переменных

43.

Задание B12 (№ 28071)
Если достаточно быстро вращать ведёрко с водой на
верёвке в вертикальной плоскости, то вода не будет
выливаться. При вращении ведёрка сила давления воды на
дно не остаётся постоянной: она максимальна в нижней
точке и минимальна в верхней. Вода не будет выливаться,
если сила её давления на дно будет положительной во
всех точках траектории кроме верхней, где она может быть
равной нулю. В верхней точке сила давления, выраженная
2
v
в ньютонах, равна P m
g , где m — масса воды в
L
килограммах, v — скорость движения ведёрка в м/с,
L — длина верёвки в метрах, g — ускорение свободного
падения (считайте, g = 10 м/с2 ). С какой наименьшей
скоростью надо вращать ведёрко, чтобы вода не
выливалась, если длина верёвки равна 62,5 cм?
Ответ выразите в м/с.

44.

Данные:
g 10 м / с2 , L 0,625 м
L 62,5 см 0,625 м
v2
P m v 2 10 , m 0, v 0.
Функция: P m g
0,625
L
Найти:
vнаим. 0 при P 0.
Решаем неравенство:
v2
m
10 0, v 0.
0,625
Так как v 0, то v 2,5.
Ответ: 2,5

45.

В презентации использованы
задачи из открытого банка
заданий ЕГЭ по математике.