ЕГЭ-2025 по математике профильного уровня

1. ЕГЭ-2025 по математике профильного уровня

математика
ЕГЭ-2025
по математике
профильного уровня
Зенкина Ирина Александровна
председатель экспертной комиссии по проверке ЕГЭ по математике,
кандидат физико-математических наук,
доцент кафедры «Высшая математика и физика» КФ МГТУ им. Н.Э. Баумана

2. Материалы для подготовки к экзамену

математика
Материалы для подготовки к экзамену
Официальный сайт ФИПИ
Демоверсия
Открытый банк
заданий
Анализ ошибок
прошлых лет

3.

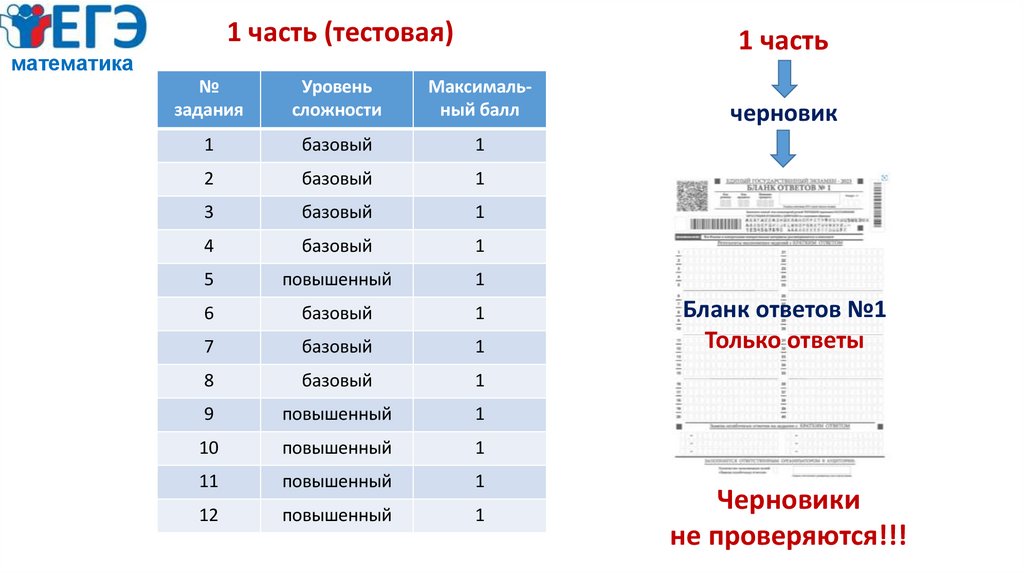
1 часть (тестовая)
1 часть
математика
№
задания
Уровень
сложности
Максимальный балл
1
базовый
1
2
базовый
1
3
базовый
1
4
базовый
1
5
повышенный
1
6
базовый
1
7
базовый
1
8
базовый
1
9
повышенный
1
10
повышенный
1
11
повышенный
1
12
повышенный
1
черновик
Бланк ответов №1
Только ответы
Черновики
не проверяются!!!

4. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
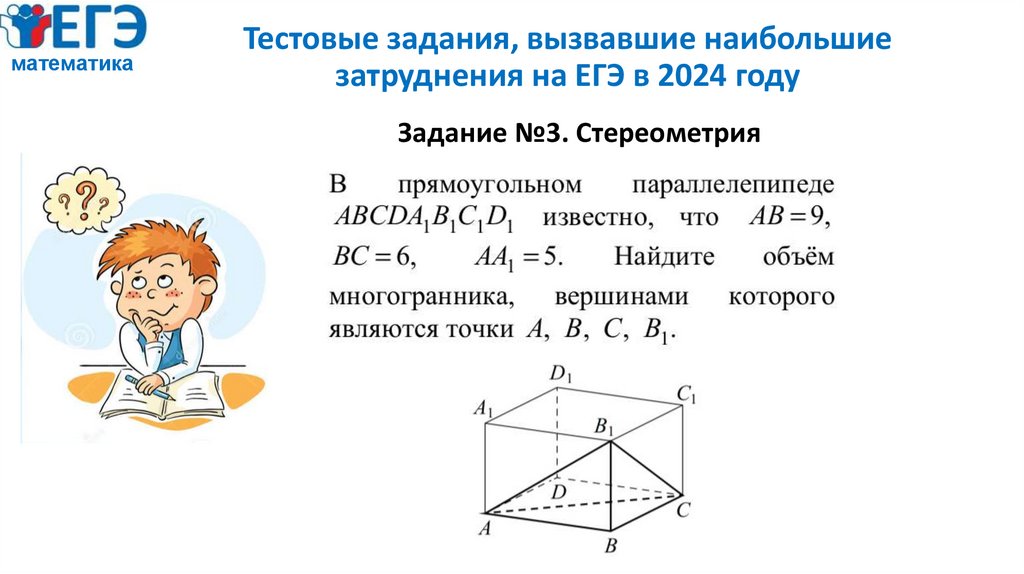
Задание №3. Стереометрия

5. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
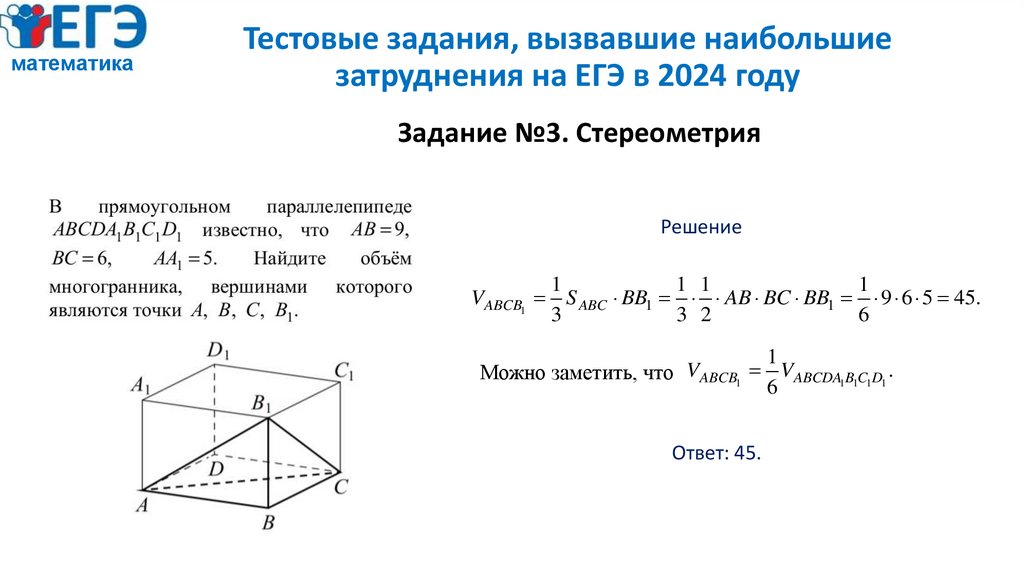
Задание №3. Стереометрия
Решение
1
1 1
1
VABCB1 S ABC BB1 AB BC BB1 9 6 5 45.
3
3 2
6
1
V
VABCDA1B1C1D1 .
Можно заметить, что ABCB1
6
Ответ: 45.

6. Что повторить?

математика
Что повторить?
1. Параллельность и перпендикулярность прямых и
плоскостей
2. Углы между прямыми, между плоскостями, между
прямой и плоскостью
3. Виды многогранников и их основные свойства
4. Виды тел вращения и их основные свойства
5. Формулы для вычисления площади поверхности
многогранников и тел вращения
6. Формулы
для
вычисления
многогранников и тел вращения
объемов

7. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
Задание №7.
Вычисления и преобразования выражений

8. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
Задание №7.
Вычисления и преобразования выражений
Решение
2 13
2
3 3 6 3 sin
12
12
3 3 6 3 sin 2
3 3 1 2sin 2
12
12
3 3 6 3 sin
3
3 3 cos 2 3 3 cos 3 3
4,5
6
2
12
Ответ: 4,5.

9. Что повторить?

математика
Что повторить?
1. Свойства степеней
2. Формулы сокращенного умножения
3. Действия с рациональными выражениями
4. Свойства логарифмов
5. Тригонометрические формулы

10. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
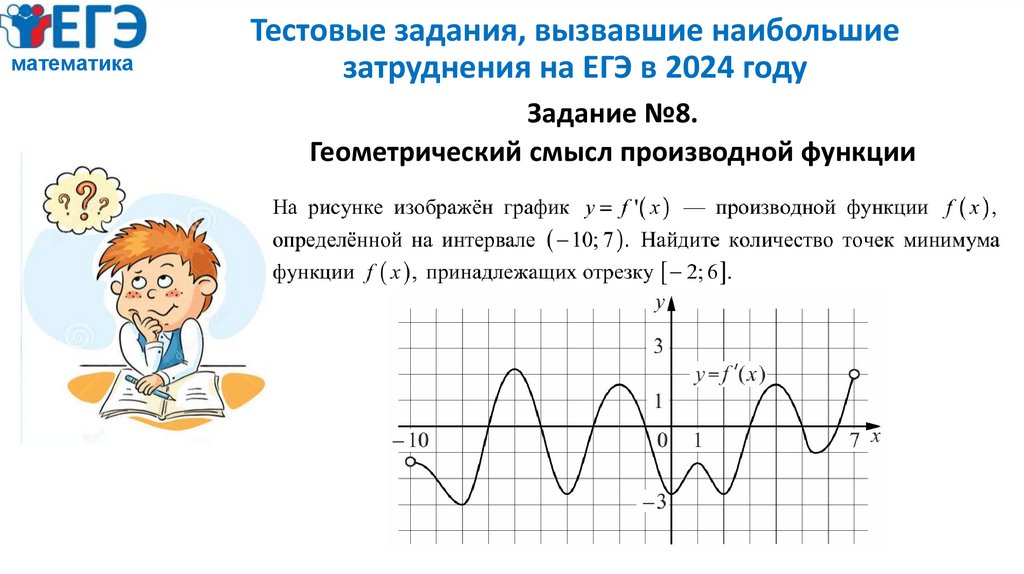
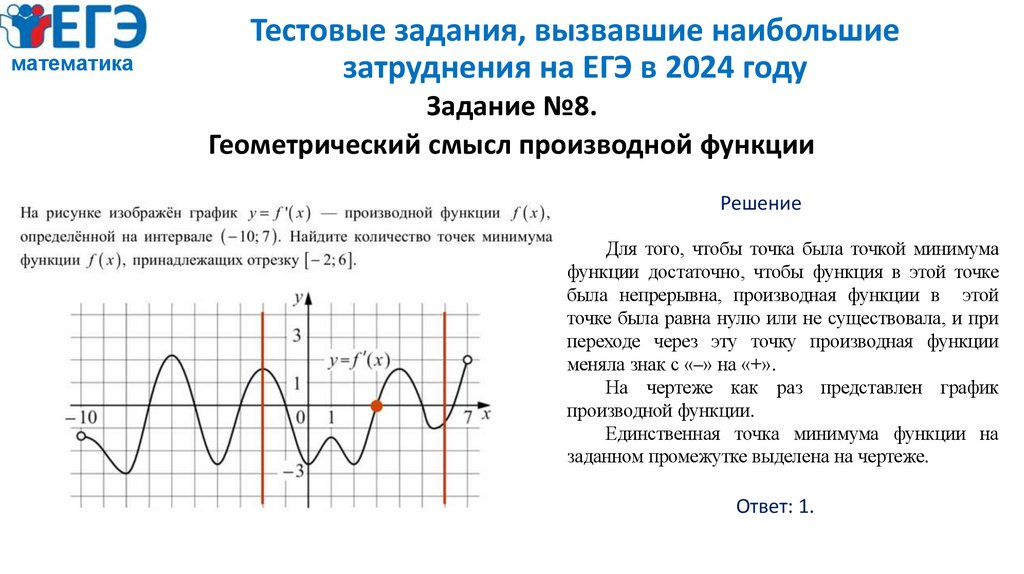
Задание №8.
Геометрический смысл производной функции

11. Тестовые задания, вызвавшие наибольшие затруднения на ЕГЭ в 2024 году

математика
Тестовые задания, вызвавшие наибольшие
затруднения на ЕГЭ в 2024 году
Задание №8.
Геометрический смысл производной функции
Решение
Для того, чтобы точка была точкой минимума
функции достаточно, чтобы функция в этой точке
была непрерывна, производная функции в этой
точке была равна нулю или не существовала, и при
переходе через эту точку производная функции
меняла знак с «–» на «+».
На чертеже как раз представлен график
производной функции.
Единственная точка минимума функции на
заданном промежутке выделена на чертеже.
Ответ: 1.

12. Что повторить?

математика
Что повторить?
1. Внимательно читать условие задачи: график
чего задан – функции или ее производной?
2. Геометрический смысл производной функции
3. Механический смысл производной функции
4. Условия возрастания и убывания функции
5. Условия
существования
минимума функции
максимума
и
6. Уравнение касательной к графику функции в
заданной точке

13.

2 часть
математика
(с развернутым ответом)
№
задания
Уровень
сложности
Максимальный балл
13
повышенный
2
14
повышенный
3
15
повышенный
2
16
повышенный
2
17
повышенный
3
18
высокий
4
19
высокий
4
2 часть
черновик
Бланк ответов №2
Развернутое
решение
и ответ
Черновики
не проверяются!!!

14. Какие математические факты можно использовать без доказательства

математика
Какие математические факты
можно использовать без
доказательства
Участник экзамена может использовать без
доказательства математические факты и формулы,
содержащиеся
в
учебниках,
входящих
в
Федеральный перечень учебников.
Если экзаменуемый использует в решении без
доказательства формулы и факты, которые не
представлены в учебниках, входящих в Федеральный
перечень, то такое решение классифицируется как
недостаточно обоснованное.

15. Задание №13. Уравнение

математика
а) Решите уравнение
2cos x sin x 2cos x.
2
3
Решение
2cos x 2cos3 x sin 2 x 0,
2cos x 1 cos 2 x sin 2 x 0,
2cos x sin 2 x sin 2 x 0,
sin 2 x 2cos x 1 0,
sin 2 x 0,
sin x 0,
x n, n Z ,
или
2 cos x 1 0,
1
cos x ,
2
2
x
2 m, m Z .
3

16. Задание №13. Уравнение

математика
9
; 3
2
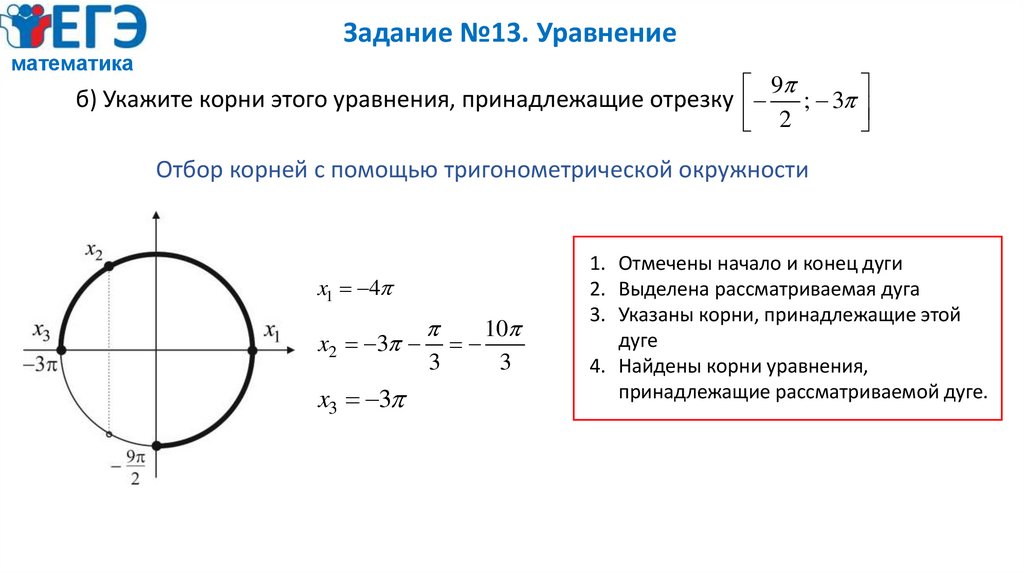
б) Укажите корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью тригонометрической окружности
x1 4
10
x2 3
3
3
x3 3
1. Отмечены начало и конец дуги
2. Выделена рассматриваемая дуга
3. Указаны корни, принадлежащие этой
дуге
4. Найдены корни уравнения,
принадлежащие рассматриваемой дуге.

17. Задание №13. Уравнение

математика
9
; 3
2
б) Укажите корни этого уравнения, принадлежащие отрезку
x n, n Z ,
9
n 3 ,
2
1
4 n 3,
2
т.к. n Z , то
n 4, x 4 ,
n 3, x 3 .
Отбор корней с помощью неравенства
2
2 m, m Z ,
3
9 2
2 m 3 ,
3
2
9 2
2m 3,
2 3
5
7
2 m 1 ,
6
12
т.к. m Z , то
m 2,
10
2
.
4
x
3
3
x
2
2 m, m Z ,
3
9
2
2 m 3 ,
2
3
9
2
2m 3,
2
3
11
1
1 m 1 ,
12
6
нет целых m.
x
Ответ: a) n, n Z ; 2 2 m, m Z ;
3
10
б ) 4 ; 3 ;
.
3
1.
2.
3.
Записаны неравенства для каждой
серии решений уравнения,
С помощью равносильных
преобразований найдены
целочисленные значения
параметра,
Для каждого целого значения
параметра найден
соответствующий корень
уравнения, принадлежащий
заданному промежутку.

18. Задание №15. Неравенство

математика
Решите неравенство
log 7 7 x 7
Решение
2
log 72 x 4
1
2 log 7 7 x 7
log 72 x 4
1
2 1 log 7 x 7
log 72 x 4
1
1,
t 4
2t 5
1 0,
2
t 4
t 2 2t 1
0,
2
t 4
t 2 2t 1
0,
2
t 4
2
t 2,
t 1,
t 2,
log 72 x 4
t 1 2 0,
t 2 t 2
t log 7 x
2 1 t 7
log 7 49 x 2 7
1
log 7 x 2,
log 7 x 1,
log 7 x 2,
1
0
x
,
49
x 7,
x 49.
1
Ответ : x 0;
; 7 ; 49;
49

19. Задание №15. Неравенство

математика
Метод интервалов
1.
2.
3.
4.
5.
Привести неравенство к виду f(x)>0 или f(x)<0.
Рассмотреть функцию f(x).
Найти область определения f(x).
Найти нули функции f(x), решив уравнение f(x) =0.
Отметить на числовой прямой область определения и нули
функции f(x).
6. Определить знаки функции на промежутках, входящих в
область определения функции.
7. Записать ответ, включив в него промежутки в соответствии со
знаком неравенства, обратив внимание на нули функции.

20. Задание №16. Задача с практическим содержанием

математика
Решение текстовой задачи
№
Этап работы
Особенности задания
1
Работа с условием и получение
математической модели.
Все введенные переменные должны быть описаны и
должна быть записана их размерность.
Математической моделью может служить уравнение,
неравенство, система уравнений или неравенств и т.п.
2
Исследование математической
модели.
Решение полученного уравнения, неравенства или их
системы.
3
Получение ответа в исходной
задаче.
Перед тем, как записать ответ к задаче, еще раз
внимательно прочитайте вопрос, обратив внимание на
размерность искомой величины.

21. Задания №14 и №17. Геометрия

математика
Все шаги решения должны быть обоснованы.
В качестве обоснования могут выступать аксиомы, теоремы,
выражающие свойства и признаки геометрических объектов,
формулы для расчета различных параметров геометрических
фигур и тел.
Советы:
Аккуратный и наглядный чертеж – основа решения задачи.
Даже если не получилось решить пункт а), обязательно
попробуйте решить пункт б), причем факт, доказательство
которого требовалось провести в пункте а), можно
использовать при решении б).

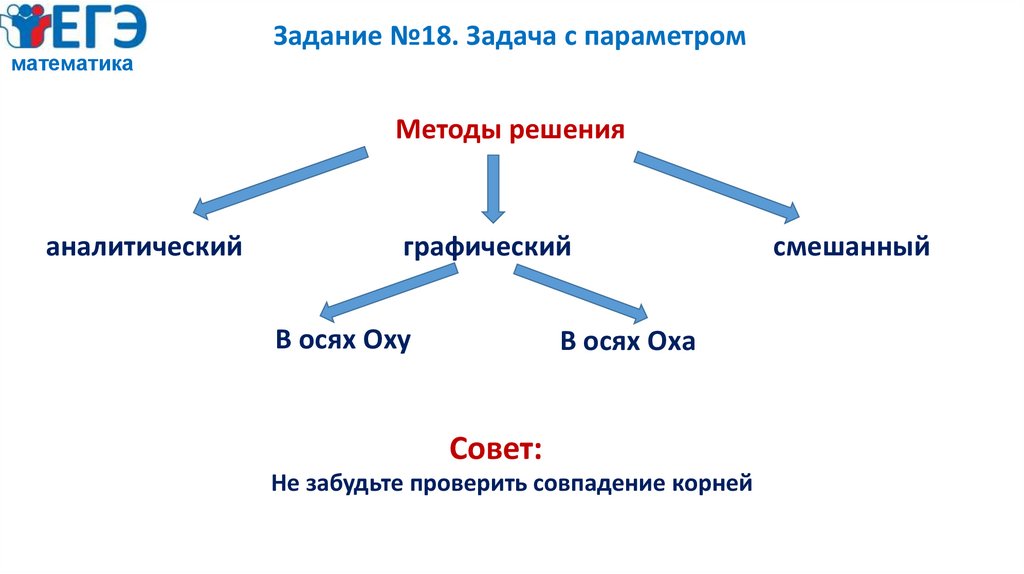
22. Задание №18. Задача с параметром

математика
Задание №18. Задача с параметром
Методы решения
аналитический
графический
В осях Оху
В осях Оха
Совет:
Не забудьте проверить совпадение корней
смешанный

23. Задание №19. Задача на теорию чисел

математика
Пункты а) и б)
Может ли быть, что ….?
да
нет
достаточно
привести пример
требуется
обоснованное
доказательство
Пункт в)
Найдите наибольшее или наименьшее значение…
Оценка
Пример, обеспечивающий точность оценки

24.

Задание №19.
математика Каждое из четырех последовательных натуральных чисел поделили на одну из его
ненулевых цифр. Сумма получившихся чисел равна S.
а) Может ли S быть равной 386?
б) Может ли S быть равной 9,125?
в) Найдите наибольшее целое значение S, если каждое из исходных чисел было
от 200 до 699 включительно.
Решение
а) Да, может, например:
109 110 111 112
109 110 111 56 386.
1
1
1
2
б) Если S=9,125, то хотя бы одно из чисел разделили на 8, причем само число было нечётным. В этом
случае цифра 8 не могла быть последней цифрой числа. Следовательно, это число не меньше 80.
Значит, при делении получается число не меньше 10. Следовательно, сумма четырех получившихся
чисел больше 10, а, значит, она не могла быть равной 9,125.
1
7
в) Если хотя бы одно из исходных чисел разделили на 2 или больше, то S 700 1 1 1 700 2450.
2
2
Если каждое из исходных чисел разделили на 1, то S равно сумме этих чисел, а среди цифр в записи
каждого из этих чисел присутствует 1. Четыре наибольших последовательных числа, не превосходящих
699 и обладающих таким свойством, это 616, 617, 618 и 619. Сумма этих чисел равна 2470, что больше,
чем 2450. Таким образом, наибольшее целое значение S равно 2470.
Ответ: а) да; б) нет; в) 2470.

25.

Ты сдашь
по математике!