Similar presentations:
Равносильность уравнений
1.
2. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение,
равносильноеданному .
3.
Если обе части уравнения умножить илиразделить на одно и то же отличное от
нуля число, то получится уравнение,
равносильное данному.
4.
Если обе части уравнения возвести водну и ту же нечетную степень, то
получится уравнение, равносильное
данному.
5.
Если к обеим частям уравненияприбавить одно и то же выражение,
имеющее смысл при всех допустимых
значениях переменной, то получится
уравнение, равносильное данному.
6.
Если обе части уравнения умножить (илиразделить) на одно и то же выражение, не
равное нулю, имеющее смысл для
любого x из области определения, то
получится уравнение, равносильное
данному.
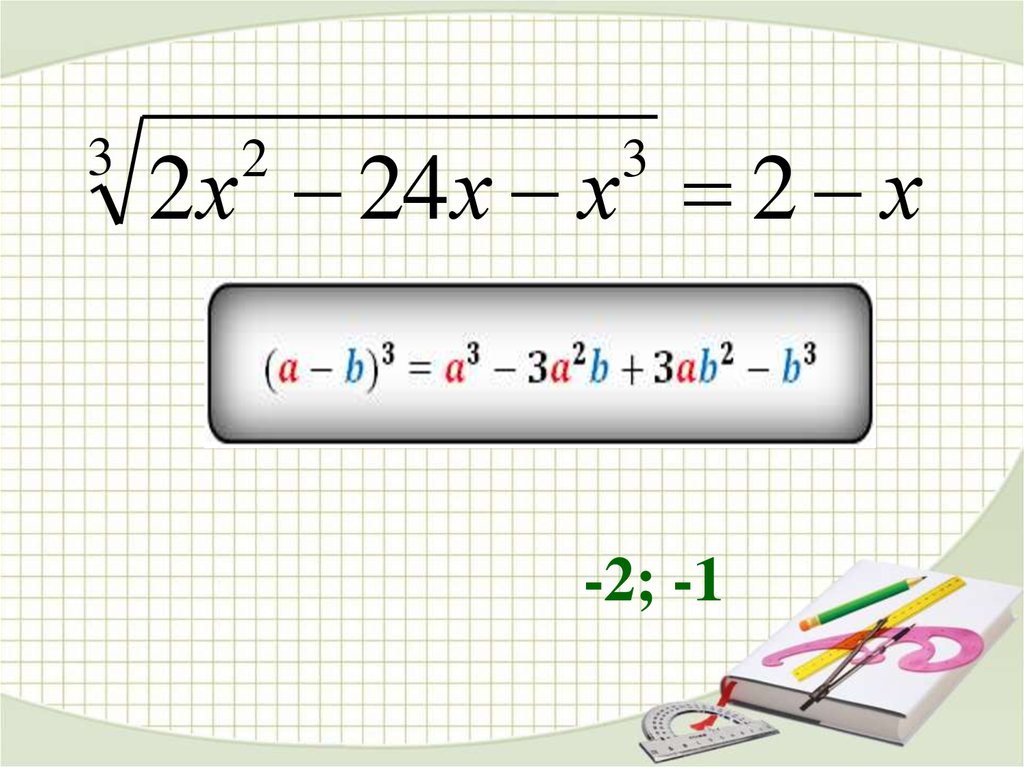
7.
32х 24х х 2 х
2
3
-2; -1
8.
92 х 3 х
2
9
-1; 3
х 6
9.
(cos 2 x 9x 4 13
) (sin x cos x 9
2
n, n Z
;
2
2 n, n Z
x 4 13
)
10.
x 6x х 3 x 3 82
6
6
4
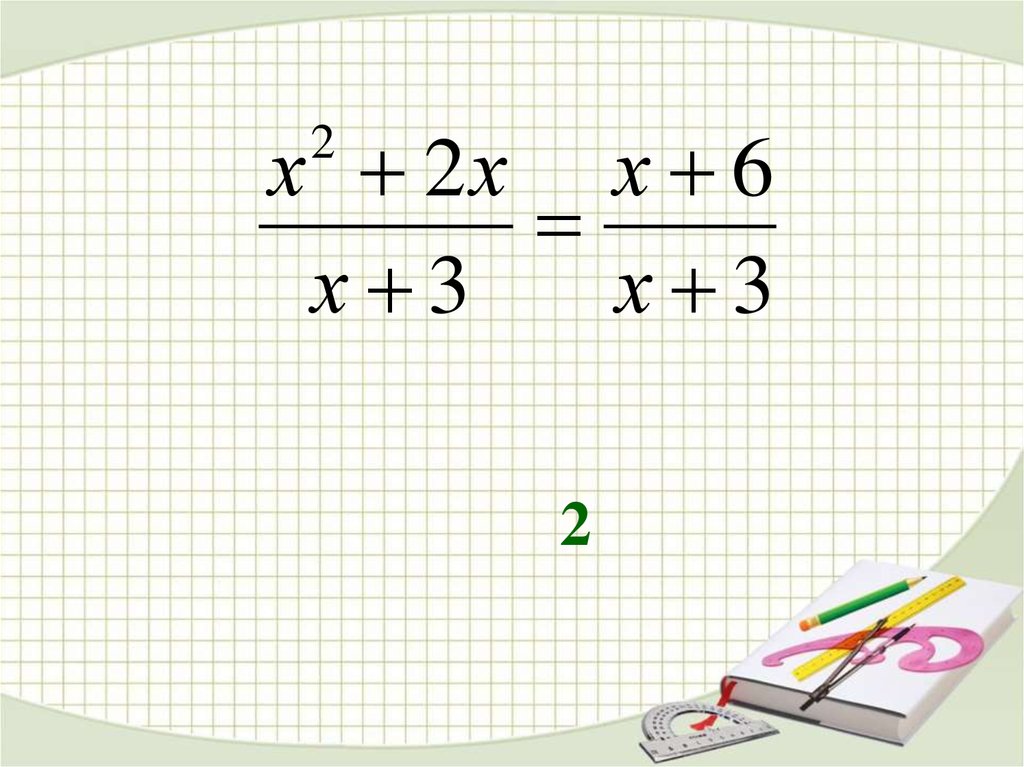
11.
х 2х х 6х 3
х 3
2
2









 mathematics
mathematics








