Similar presentations:
Квадратичная функция, её график и свойства
1.
«Квадратичнаяфункция, её
график и свойства»
2.
Алгоритм построения графика1.
Найти координаты вершины параболы и отметить её на
плоскости.
2.
Определить направление ветвей.
3.
Провести ось симметрии параболы.
4.
Найти точки пересечения параболы с осями координат.
5.
Построить, если нужно, дополнительные точки.
6.
Провести через точки параболу.
3.
Построить график функции у= -х2+6х-51.Координаты вершины: х0 = -в: (2а)=-6: (2*(-1))= -6: (-2)=3,
У0= -32+6*3-5=-9+18-5=18-14=4. Значит вершина параболы точка А(3;4)
2. Ветви параболы направлены вниз, т.к. а=-1.
3. Ось симметрии параболы х=3.
4.Точки пересечения параболы с осью ох, когда у=0. Решу уравнение:
-х2+6х -5=0 или х2-6х+5=0, по теореме Виета корни будут равны
х1=1 и х2=5. Значит, парабола будет пересекать ось ох в этих точках.
На оси оу х=0, значит у= 02+6*0-5=0+0-5=-5-это и будет точка
пересечения оси оу.
4. Возьму дополнительные точки. При х=2, у=-22+6*2-5=-4+12-5=12-9=3.
Это будет точка В(2;3) и ей будет симметрична точка Д(4;3).
Соединю полученные точки.
4.
График функции у=2
-х +6х-5
y
.
. .
A
4
3
0
.
-5
B
.
C
.
x
1 2 3 4 5
.
D
5.
Определение свойств функциипо графику
1.
Найти координаты вершины параболы и отметить её на
плоскости.
2.
Определить направление ветвей.
3.
Провести ось симметрии параболы.
4.
Найти точки пересечения параболы с осями координат.
5.
Построить, если нужно, дополнительные точки.
6.
Провести через точки параболу.
6.
График функции у= 2х2-4х+3.
C
y
. .
.
.
3
-2 -1
0
-5
.
9
D
B
.
1 A
1 2 3 4 5
.
x
7.
Домашнее заданиеПостроить графики
2
функций у=х -3х-10 и
2
у=-3х +6х-8
и перечислить их свойства



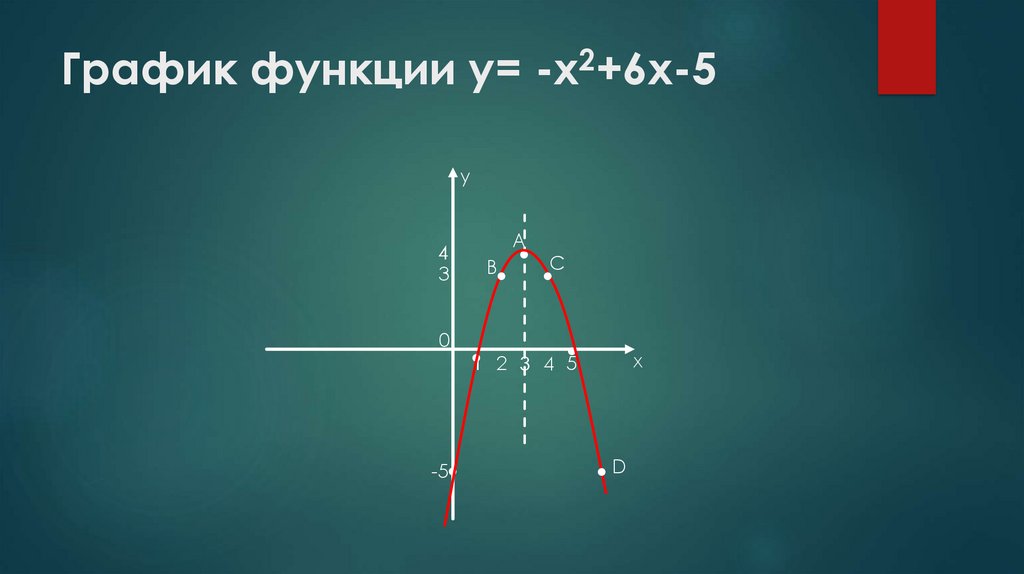



 mathematics
mathematics








