Similar presentations:
Признак перпендикулярности двух плоскостей
1. Признак перпендикулярности двух плоскостей
ПРИЗНАКПЕРПЕНДИКУЛЯРНОСТИ ДВУХ
ПЛОСКОСТЕЙ
Выполнила
Маркелова Екатерина
Учитель Кононина Т.В.
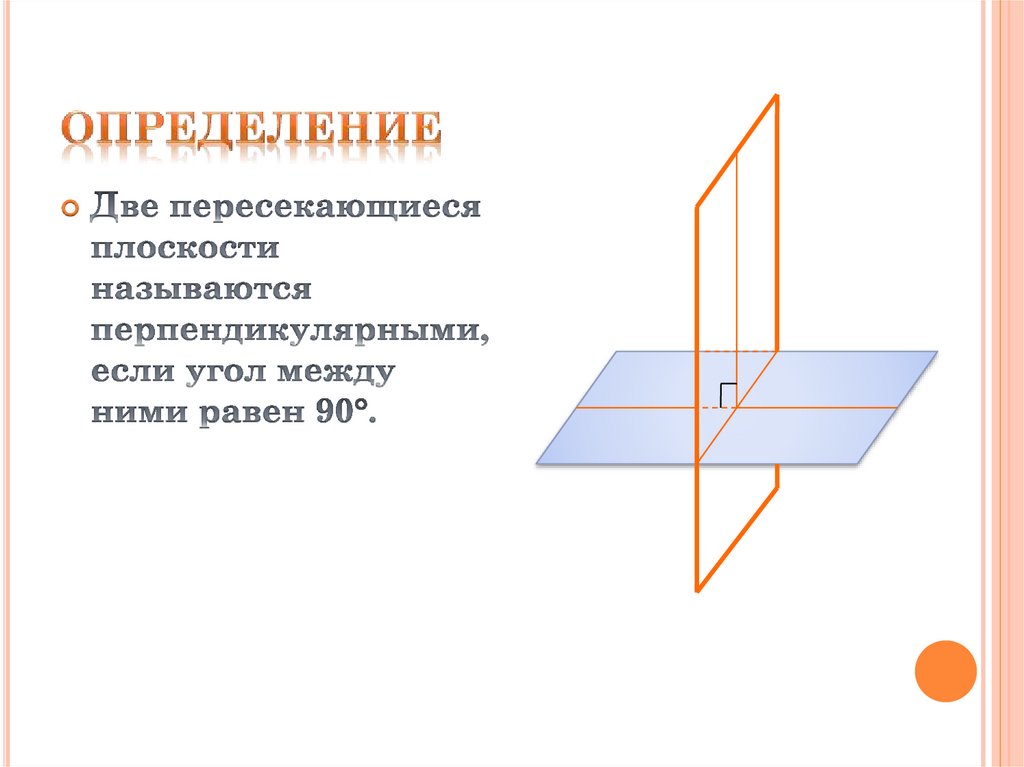
2. Определение
3. пример
Примером взаимноперпендикулярных
плоскостей служат
плоскости стены и
пола комнаты.
4. теорема
BЕсли одна из двух
плоскостей проходит
через прямую ,
перпендикулярную к
другой плоскости, то
такие плоскости
перпендикулярны.
C
D
β
A
α
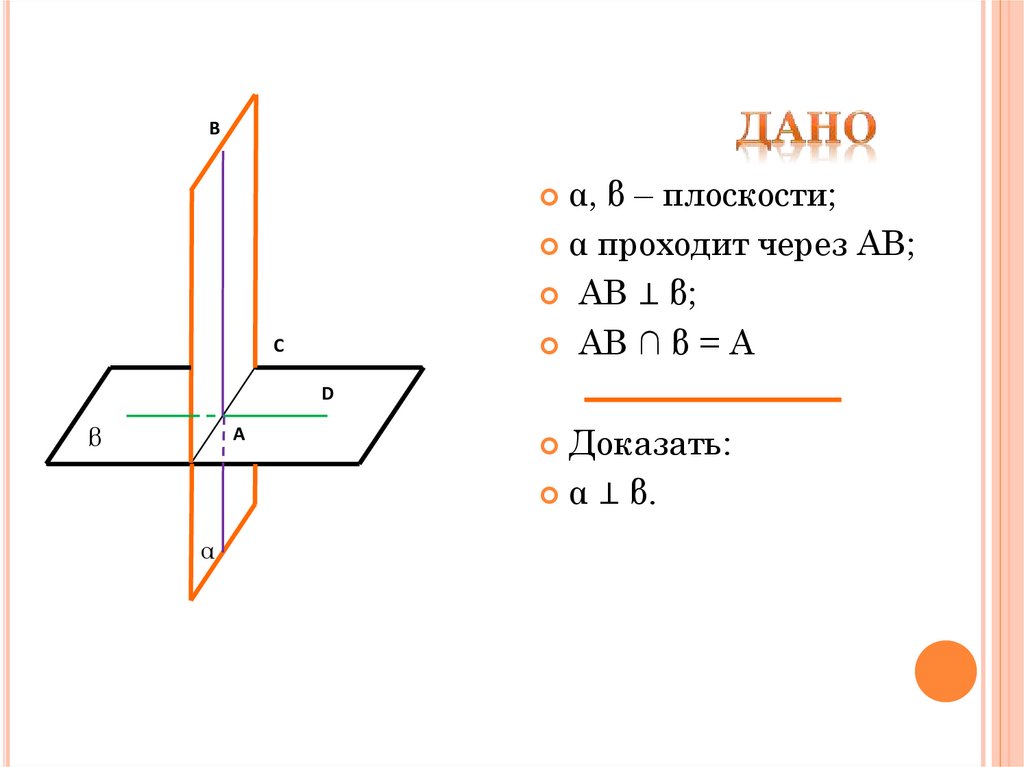
5. Дано
Bα, β – плоскости;
α проходит через AB;
AB ⊥ β;
AB ∩ β = A
C
D
β
A
α
Доказать:
α ⊥ β.
6. Доказательство
Bα ∩ β = AC,
Причем AB ⊥ AC,
т.к. по условию AB ⊥ β,
Следовательно, прямая
AB перпендикулярна к
любой прямой ,
лежащей в плоскости β.
C
D
β
A
α
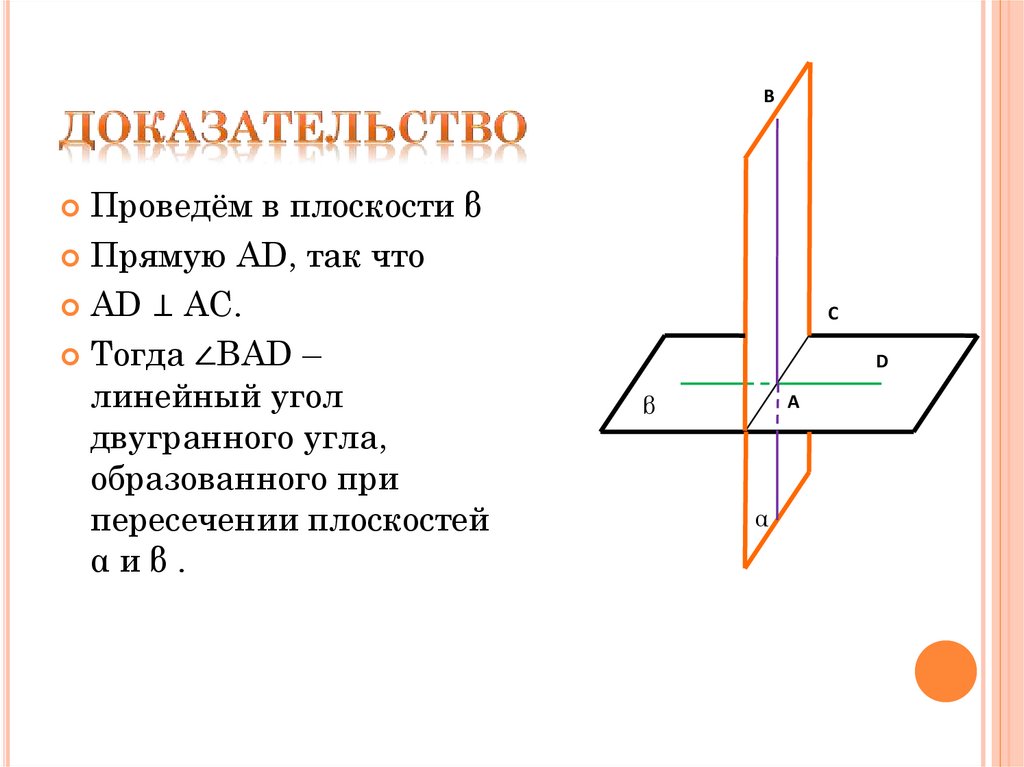
7. Доказательство
BПроведём в плоскости β
Прямую AD, так что
AD ⊥ AC.
Тогда ∠BAD –
линейный угол
двугранного угла,
образованного при
пересечении плоскостей
αиβ.
C
D
β
A
α
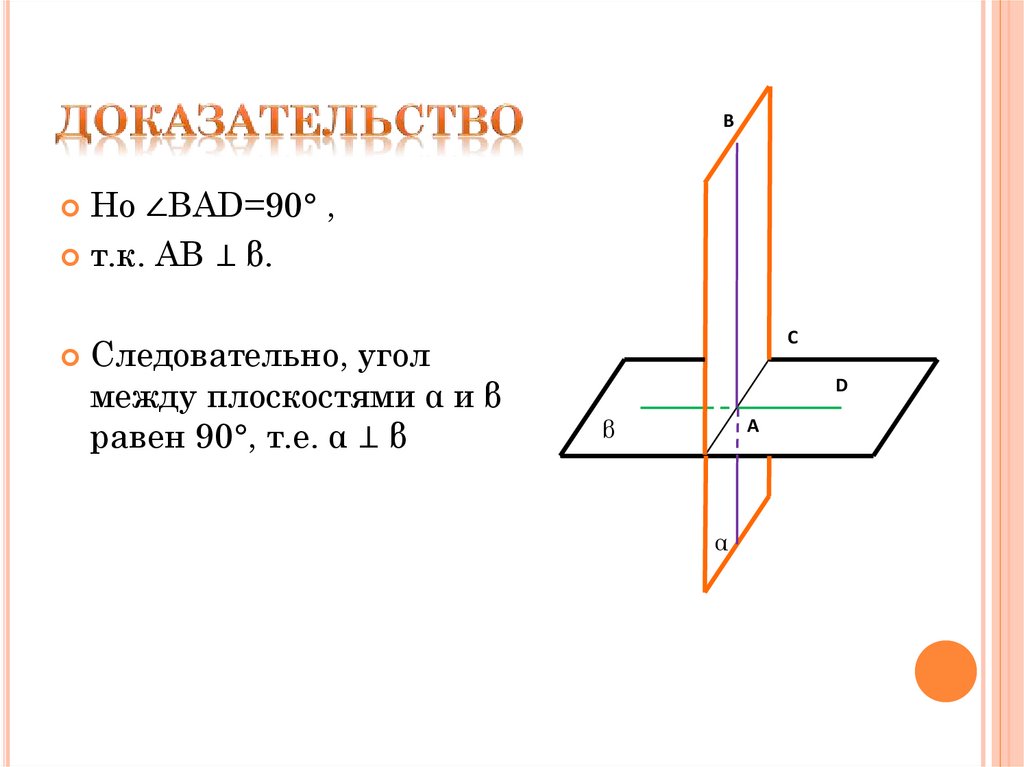
8. Доказательство
BНо ∠BAD=90° ,
т.к. AB ⊥ β.
Следовательно, угол
между плоскостями α и β
равен 90°, т.е. α ⊥ β
C
D
β
A
α
9. следствие
αПлоскость,
перпендикулярная к
прямой, по которой
пересекаются две данные
плоскости,
перпендикулярна к
каждой из этих
плоскостей.
γ
a
β





 mathematics
mathematics